CRYPTOGRAPHIC PROTOCOLS 2015 LECTURE 4 Elgamal INDCPA Security

CRYPTOGRAPHIC PROTOCOLS 2015, LECTURE 4 Elgamal. IND-CPA Security. Malleability Helger Lipmaa University of Tartu, Estonia

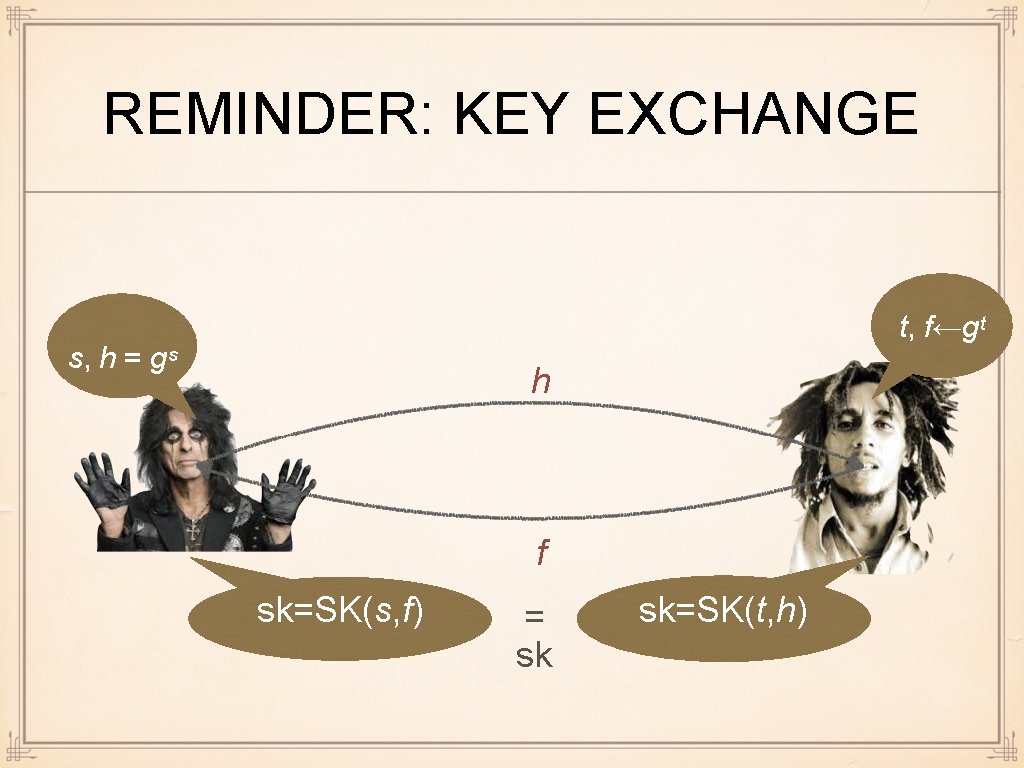
UP TO NOW Assumptions, reductions Basic assumptions in DL family: DL, CDH, DDH (DH)KE. Security of KE <=> assumptions Owners of public keys can agree on joint secret key

REMINDER: KEY EXCHANGE I want to send secret information to Bob, but he is in Jamaica Let us agree on a joint secret key for further communicat ion

SECURE COMPUTATION I want to know whether I have more hash than Bob but I do not want to reveal how much I have Let us do secure computati on of "≥" Millionaires' protocol Ditto

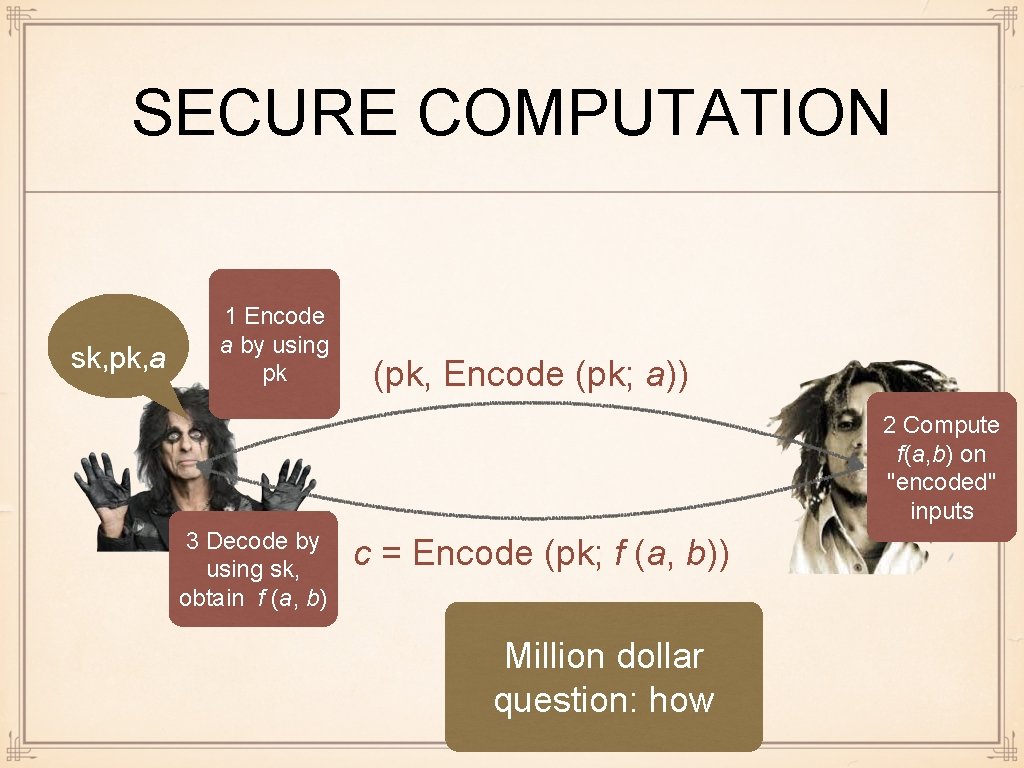
SECURE COMPUTATION sk, pk, a 1 Encode a by using pk (pk, Encode (pk; a)) 2 Compute f(a, b) on "encoded" inputs 3 Decode by using sk, obtain f (a, b) c = Encode (pk; f (a, b)) Million dollar question: how

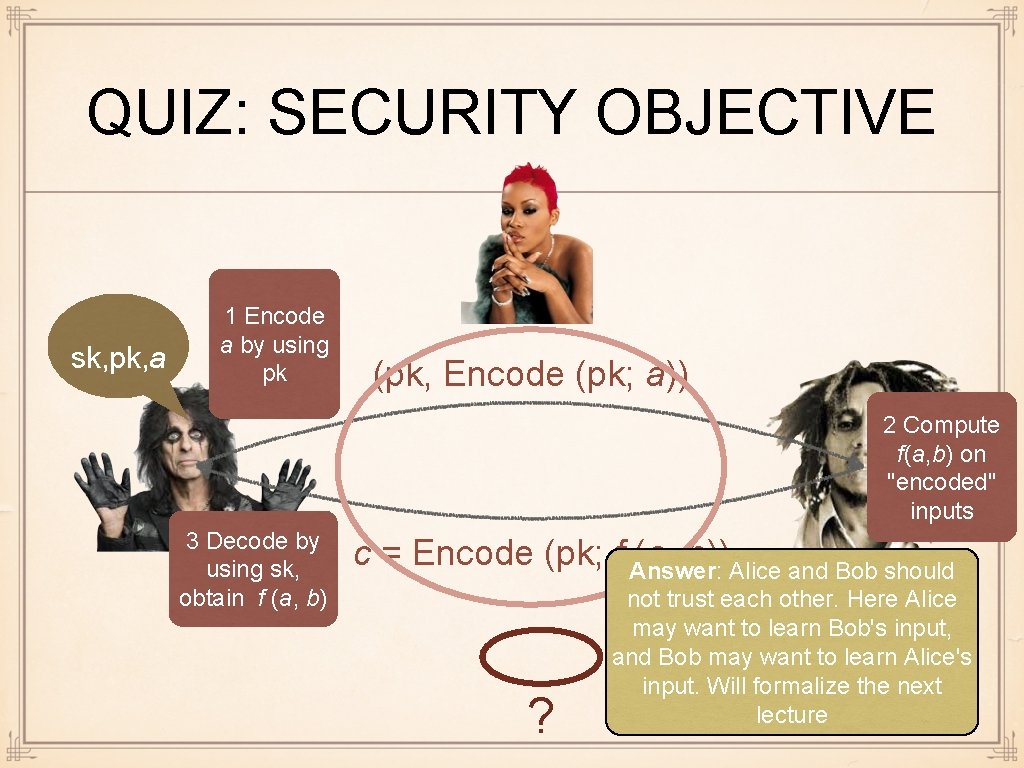
QUIZ: SECURITY OBJECTIVE sk, pk, a 1 Encode a by using pk (pk, Encode (pk; a)) 2 Compute f(a, b) on "encoded" inputs 3 Decode by using sk, obtain f (a, b) c = Encode (pk; f (a, b)) ?

QUIZ: SECURITY OBJECTIVE sk, pk, a 1 Encode a by using pk (pk, Encode (pk; a)) 2 Compute f(a, b) on "encoded" inputs 3 Decode by using sk, obtain f (a, b) c = Encode (pk; f Answer: (a, b))Alice and Bob should ? not trust each other. Here Alice may want to learn Bob's input, and Bob may want to learn Alice's input. Will formalize the next lecture

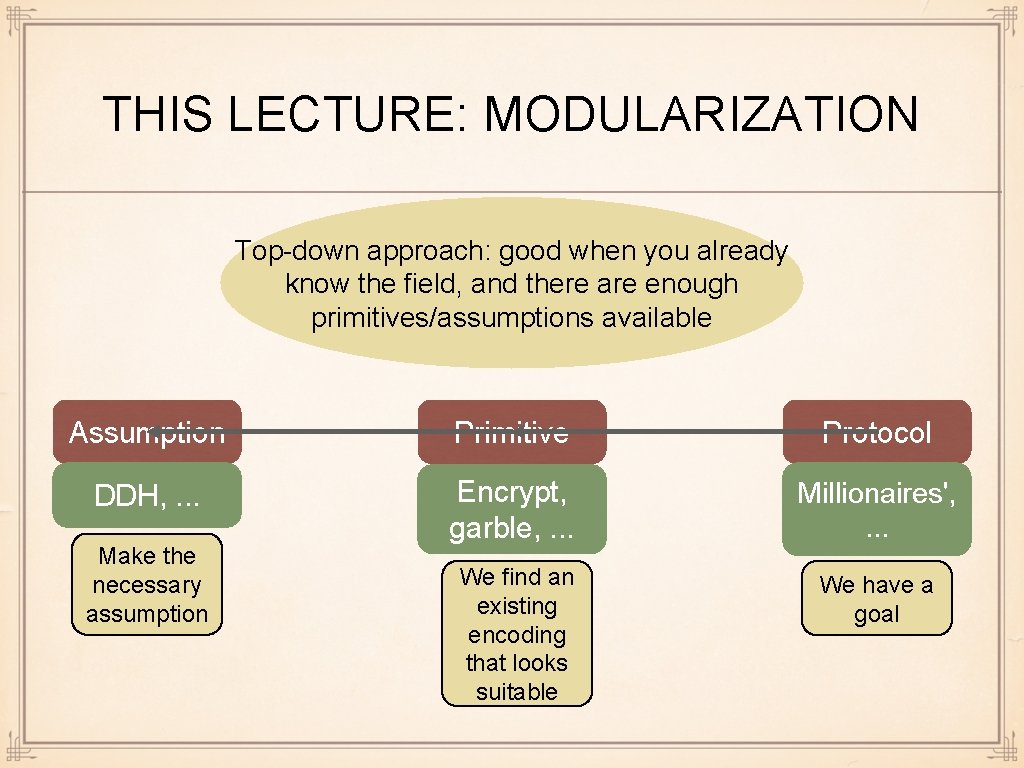
THIS LECTURE: MODULARIZATION Top-down approach: good when you already know the field, and there are enough primitives/assumptions available Assumption Primitive Protocol DDH, . . . Encrypt, garble, . . . Millionaires', . . . We find an existing encoding that looks suitable We have a goal Make the necessary assumption

THIS LECTURE: MODULARIZATION We know assumption We build some encoding on top of it We build the final protocol on top of it Assumption Primitive Protocol DDH, . . . Encrypt, garble, . . . Millionaires', . . . Bottom-up approach: good for teaching, research (easier to start with basics) and getting papers published

THIS LECTURE: MODULARIZATION We know assumption We build some encoding on top of it Assumption Primitive DDH Elgamal (homomorphic encryption) Encrypt Bottom-up approach: good for teaching, research (easier to start with basics) and getting papers published

REMINDER: KEY EXCHANGE t, f←gᵗ s, h = gˢ h f sk=SK(s, f) = sk sk=SK(t, h)

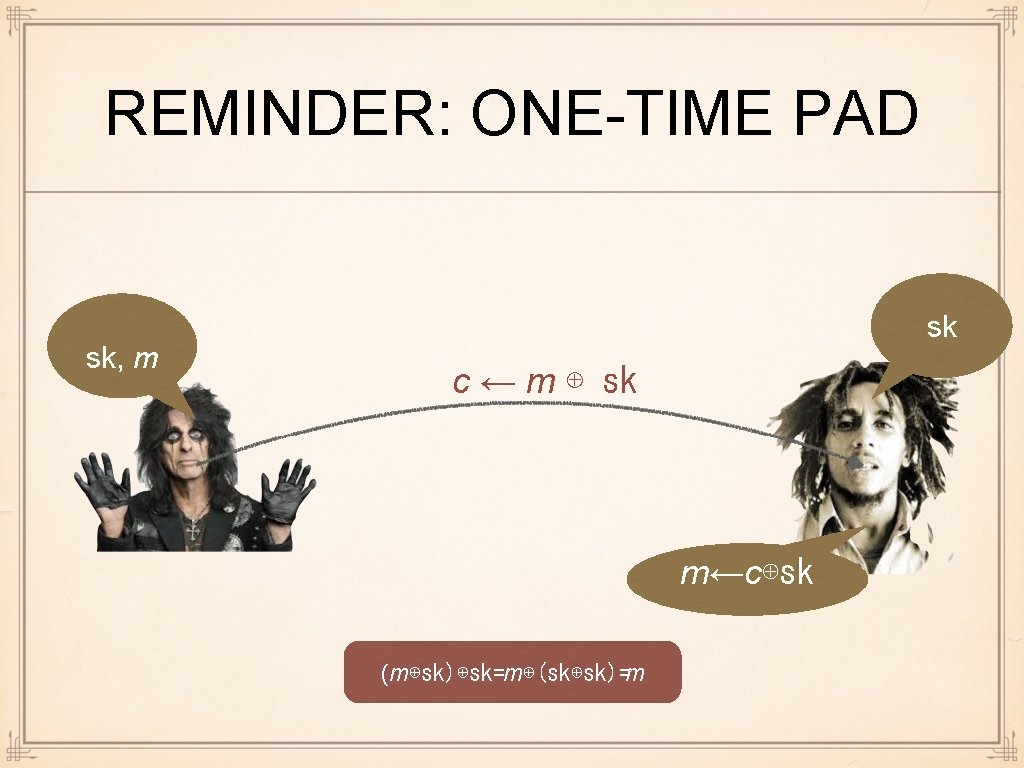
REMINDER: ONE-TIME PAD sk, m sk c ← m ⊕ sk m←c⊕sk (m⊕sk)⊕sk=m⊕(sk⊕sk)=m

HOW TO COMBINE We have key-exchange Returns secret key sk₁. . . and one-time pad Returns ciphertext, given sk₂ However, they work in different domains sk₁ is a group element, sk₂ is a bit-string

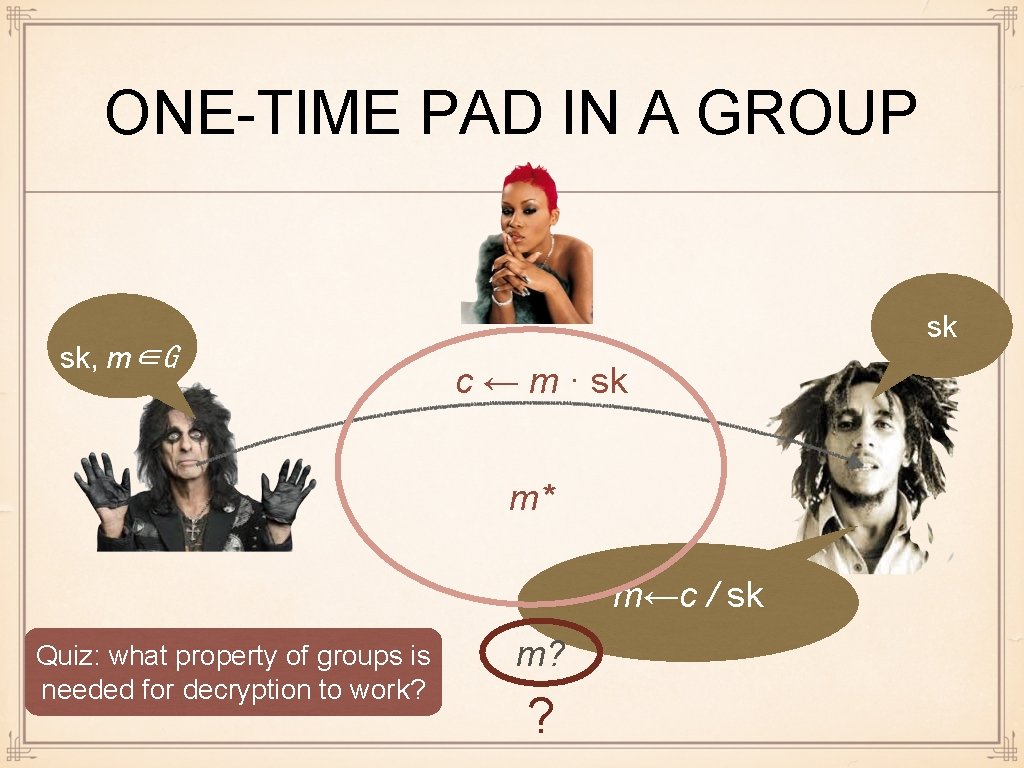
ONE-TIME PAD IN A GROUP sk, m∈G sk c ← m · sk m* m←c / sk Quiz: what property of groups is needed for decryption to work? m? ?

SECURITY INTUITION If sk is uniformly distributed in G, then m · sk is also uniformly distributed For all m ∈ G*, c ∈ G: Pr [m · sk = c] = Pr [sk = c / m] = 1 / q Thus, an adversary who only sees c, has no information about m

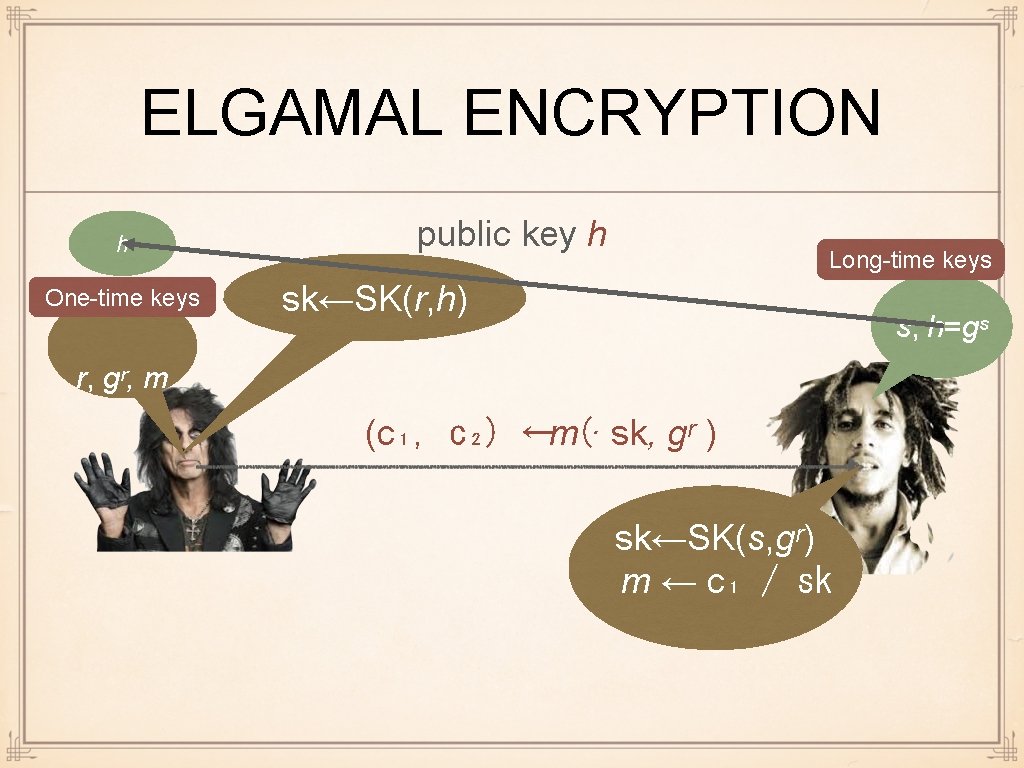
ELGAMAL ENCRYPTION h One-time keys public key h Long-time keys sk←SK(r, h) s, h=gˢ r, gʳ, m (c₁, c₂) ←m(· sk, gʳ ) sk←SK(s, gʳ) m ← c₁ / sk

ELGAMAL ENCRYPTION Elgamal. Setup (κ): hb 1. Choose a group G of order q where One-time keys breaking DDH hassk←SK(r, pk) complexity 2^κ 2. Choose a generator g of G 3. Return gk ← desc (G) = (. . . , q, g) r, h←gˆr Elgamal. Keygen (gk): Long-time keys 1. s ← ℤq 2. pk = h ← gˢ 3. Return (s, h) /* secret key, public key sk, pk */ (c₁, c₂) ←m(· sk, h) Elgamal. Enc (gk, h; m, r): Elgamal. Dec (gk, s; c₁, c₂): 1. /* Assumes r ← R: randomized alg. */ 2. (c₁, c₂)←( mhʳ, gʳ) 3. Return (c₁, c₂) 1. m ← c₁ / c₂ ˢ 2. Return m For the sake of simplicity, we assume that gk is a fixed system parameter, shared by all participants. Will not mention gk unless explicitly needed

CORRECTNESS: FORMALLY Key generation: h = gˢ Encryption: (c₁, c₂) = Ench; (m, r) = (mhʳ, gʳ) Decryption: c₁ / c₂ ˢ = mgʳˢ / gʳˢ = m Thus decryption is always successful

SECURITY: INTUITION Elgamal = DHKE + one-time pad DHKE is whatke-secure under X assumption one-time pad is unconditionally secure => Elgamal is whatenc-secure under X assumption But how to formalize?

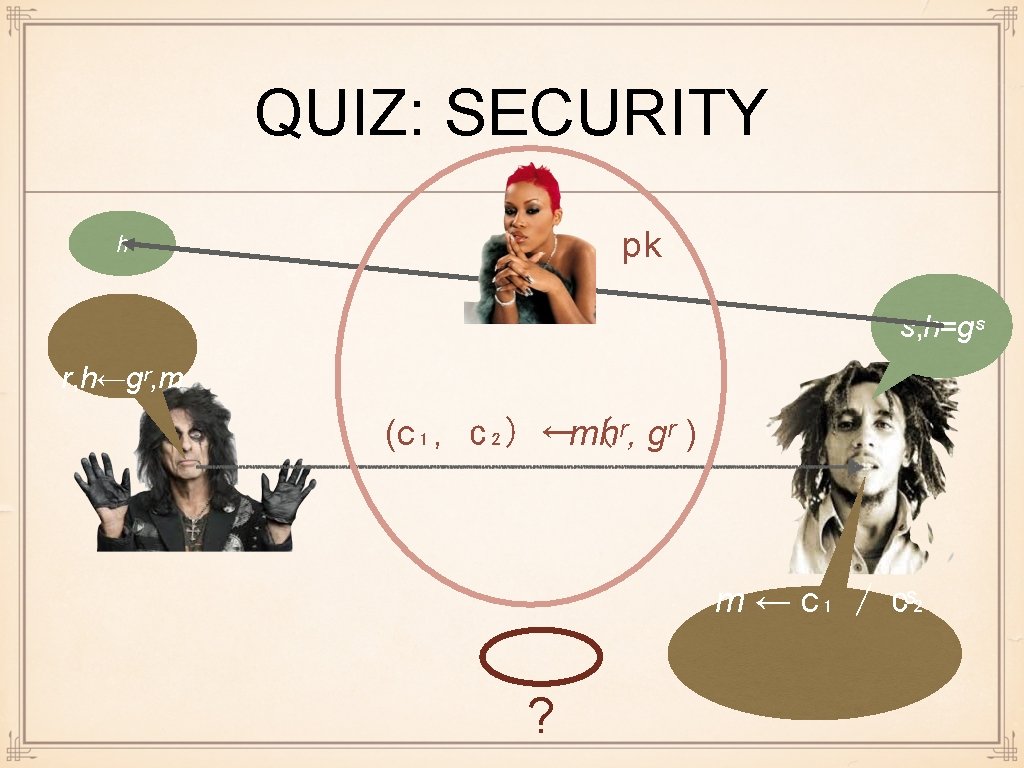
QUIZ: SECURITY pk h s, h=gˢ r, h←gʳ, m (c₁, c₂) ←mhʳ, ( gʳ ) m ← c₁ / c₂ ˢ ?

ENCRYPTION SECURITY: ISSUES Message recovery security: Eve should not be able to compute m Just difficulty of computing m is not good enough Like KR security was not enough in KE Need indistinguishability again

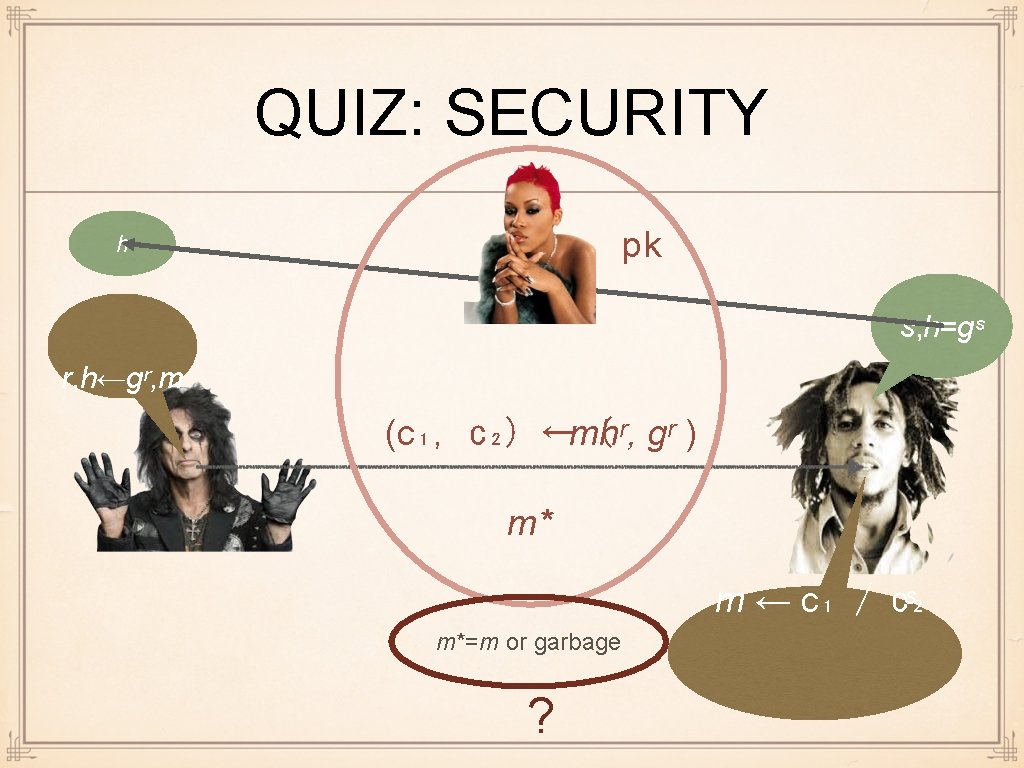
QUIZ: SECURITY pk h s, h=gˢ r, h←gʳ, m (c₁, c₂) ←mhʳ, ( gʳ ) m* m ← c₁ / c₂ ˢ m*=m or garbage ?

REAL-RANDOM / LEFT-RIGHT Real-Random indistinguishability: Adversary cannot distinguish the real plaintext m from a random plaintext Encrypt "I owe Even if she has chosen m herself 100$"or else Left-Right indistinguishability: Adversary cannot distinguish a random ciphertext of m₀ He encrypted from a random ciphertext of m₁ "start a Even if she has chosen both m₀ and m₁ herself battle"or "do not start a battle". Which one?

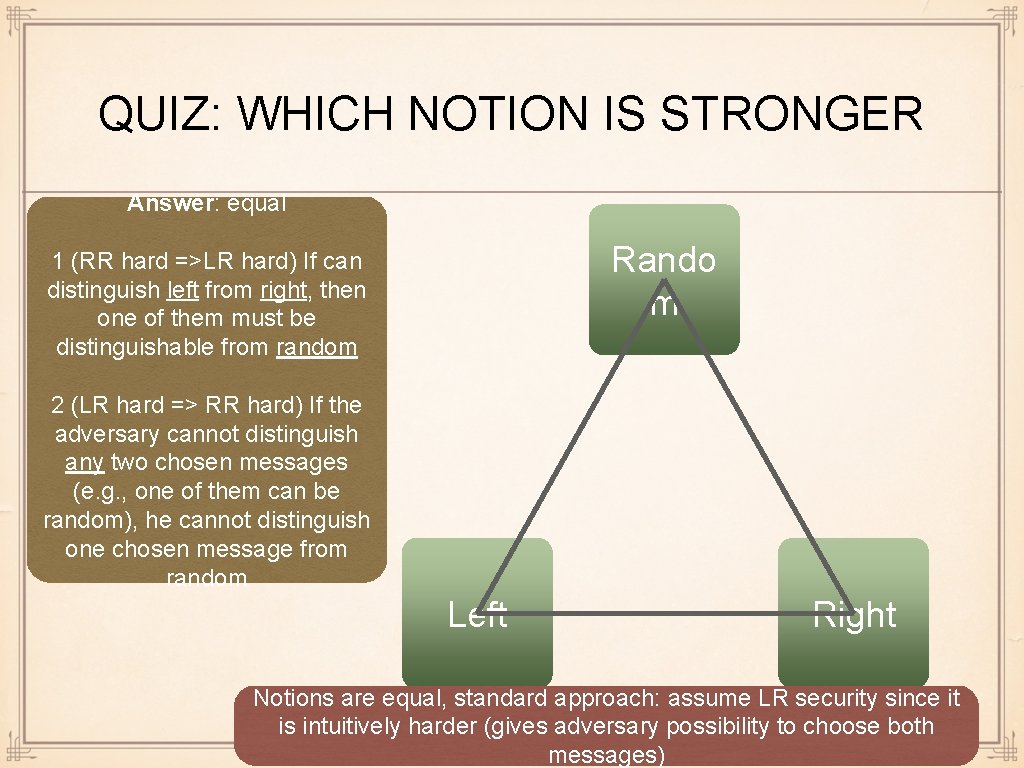
QUIZ: WHICH NOTION IS STRONGER Answer: equal Rando m 1 (RR hard =>LR hard) If can distinguish left from right, then one of them must be distinguishable from random 2 (LR hard => RR hard) If the adversary cannot distinguish any two chosen messages (e. g. , one of them can be random), he cannot distinguish one chosen message from random Left Right Notions are equal, standard approach: assume LR security since it is intuitively harder (gives adversary possibility to choose both messages)

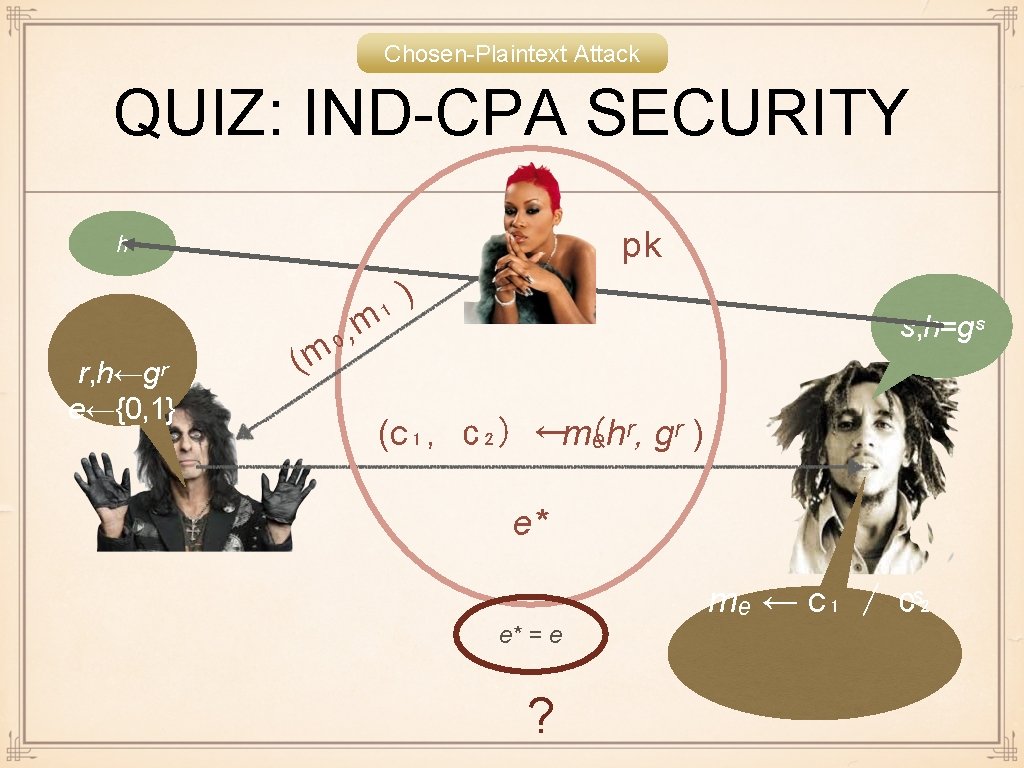
Chosen-Plaintext Attack QUIZ: IND-CPA SECURITY pk h r, h←gʳ e←{0, 1} ( , ₀ m ) ₁ m s, h=gˢ (c₁, c₂) ←mₑhʳ, ( gʳ ) e* mₑ ← c₁ / c₂ ˢ e* = e ?

IND-CPA SECURITY Π = (Setup, Keygen, Enc, Dec) Game IND(κ, Π, A) Adv[IND] : = | Pr[IND = 1] - 1 / 2 | A ε-breaks IND-CPA security of Π iff Adv[IND] ≥ ε Π is (τ, ε)-IND-CPA secure iff no adversary ε-breaks IND-CPA security of Π in time ≤ τ Π is IND-CPA secure iff it is (poly(κ), negl(κ))-IND-CPA secure gk ← Setup (κ) (s, h) ← Keygen (κ) (m₀, m₁) ←A (h) e ← {0, 1} r ←R c ← Enc (h; mₑ, r) e* ← A (h, c) Return e = e* ? 1 : 0

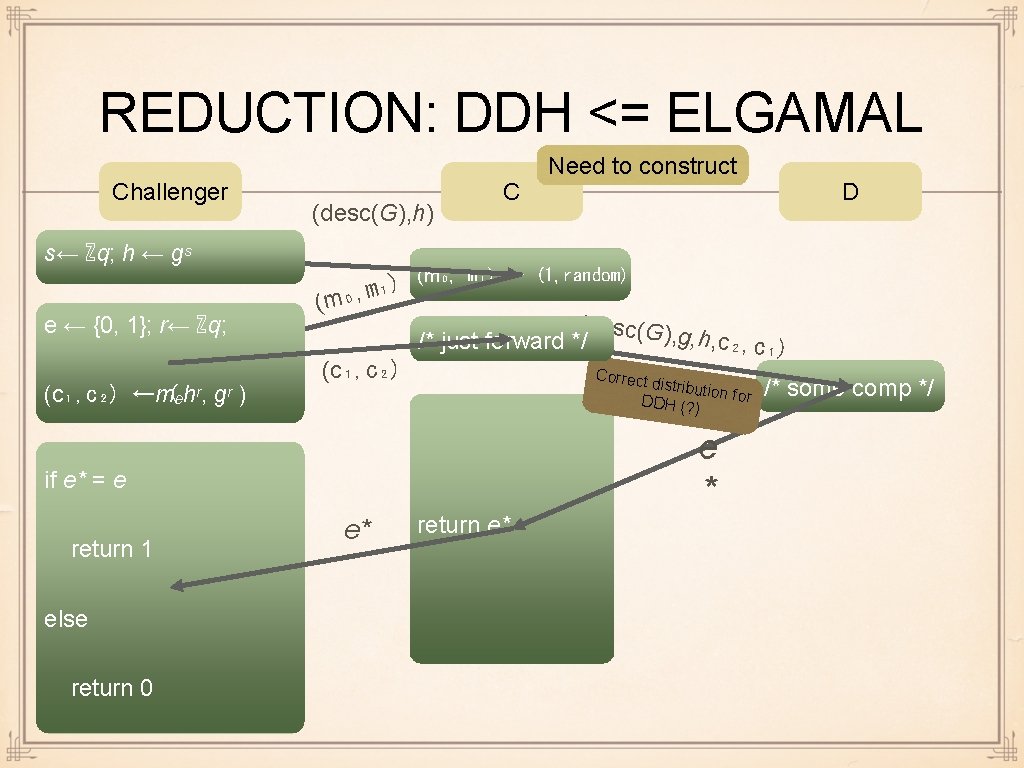
ELGAMAL IS IND-CPA SECURE Theorem. If G is a (≈τ, ≈ε)-DDH group, then Elgamal is (τ, ε)-IND-CPA secure in G. Proof idea. Reduction to absurd: we show that if Elgamal is not secure in G, then DDH must be easy in G. Elgamal is not secure => there exists an adversary D that breaks Elgamal We show DDH is easy by constructing an adversary C that breaks DDH C can use help from adversary D, by sending inputs to D and receiving outputs Simple, a home exercise

. . . TAUTOLOGY Theorem. If Elgamal is (τ + small, ε)-IND-CPA secure, then G is (τ, ε)-DDH group. (Thus, equivalent) Proof idea. Reduction to absurd: we show that if DDH is not secure in G, then breaking Elgamal must be easy in G. DDH is not secure => there exists an adversary D that breaks DDH Show Elgamal is easy by constructing an adversary C that breaks Elgamal C uses help from adversary D, sending inputs to D and receiving outputs

MAIN IDEA Recall: h = gˢ, (c₁, c₂) = Enc (h; m, r) = (mhʳ, gʳ) Hence (g, h, c₂, c₁) =(g, gˢ, gʳ, mgʳˢ) If m = 1: (g, h, c₂, c₁) is a random DDH tuple If m = random: DDH assumption: indistinguishable (g, h, c₂, c₁) is a random non-DDH tuple since random * anything = random in cyclic group

REDUCTION: DDH <= ELGAMAL Challenger (desc(G), h) s← ℤq; h ← gˢ e ← {0, 1}; r← ℤq; (c₁, c₂) ←mₑhʳ, ( gʳ ) (m ₀, m₁) (c₁, c₂) C (desc(G) , g, h, c₂, c /* just forward */ ₁) Correct distributi on for DDH (? ) e * else return 0 e* D (m₀, m₁) ← (1, random) if e* = e return 1 Need to construct return e* /* some comp */

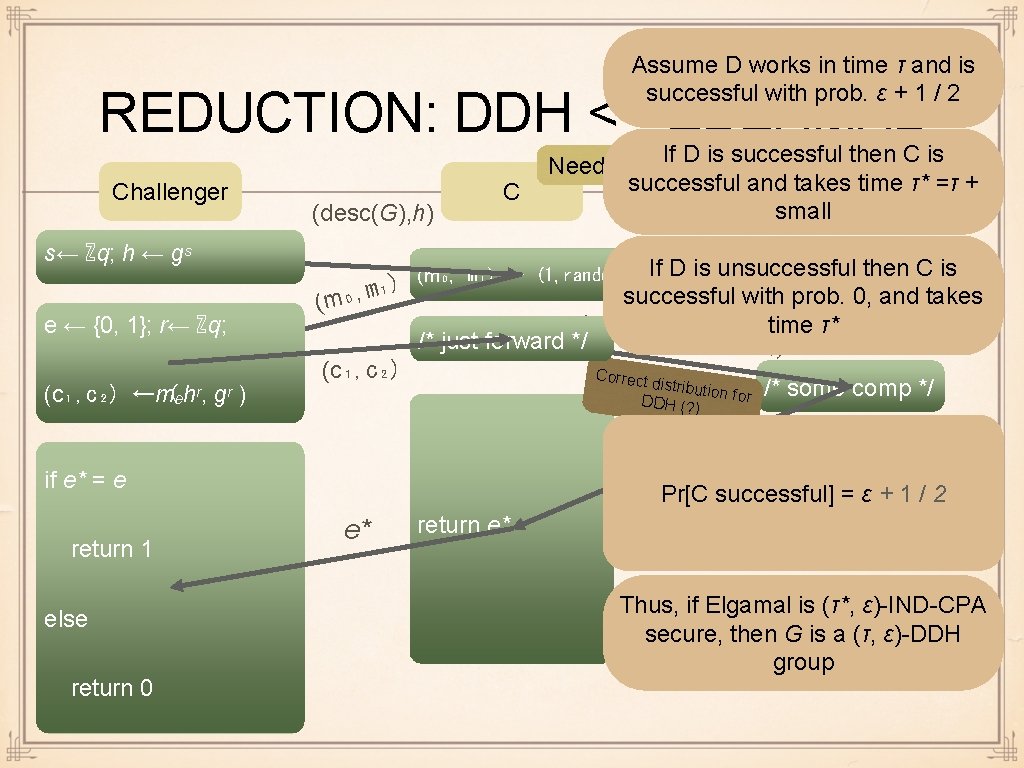
Assume D works in time τ and is successful with prob. ε + 1 / 2 REDUCTION: DDH <= ELGAMAL Challenger s← ℤq; h ← gˢ e ← {0, 1}; r← ℤq; (c₁, c₂) ←mₑhʳ, ( gʳ ) (desc(G), h) C If D is unsuccessful then C is ₁) m , ₀ successful with prob. 0, and takes (m (desc(G) time τ* , g , h , c₂, c₁) /* just forward */ (c₁, c₂) Correct distributi on for /* some comp */ D (m₀, m₁) ← (1, random) DH (? ) e Pr[C*successful] = ε + 1 / 2 if e* = e return 1 else return 0 If D is successful then C is Need to construct successful and takes. Dtime τ* =τ + small e* return e* Thus, if Elgamal is (τ*, ε)-IND-CPA secure, then G is a (τ, ε)-DDH group

IND-CPA AND BEYOND Actual security requirements even more stringent IND-CPA security only demonstrates basic concepts Bob must be sure c really came from Alice Crypto is full of Authentication, non-malleability trade-offs: do we want malleability or not? In protocol design, malleability is very useful

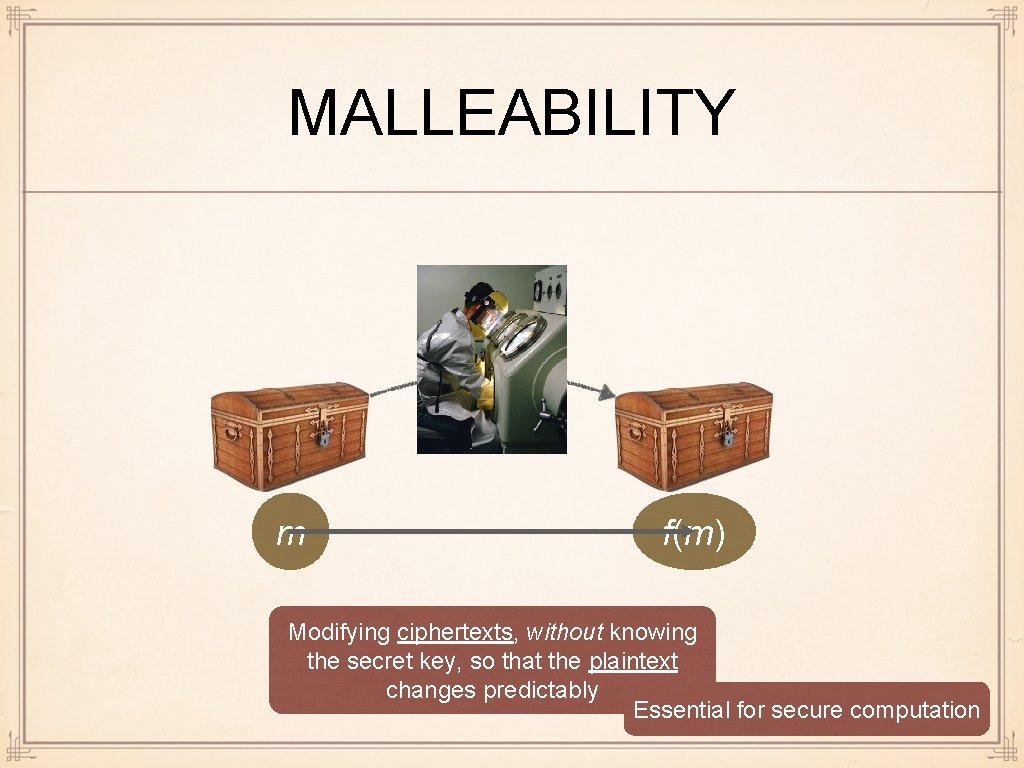
MALLEABILITY m f(m) Modifying ciphertexts, without knowing the secret key, so that the plaintext changes predictably Essential for secure computation

MALLEABILITY OF ELGAMAL Recall: Enc (h; m, r) = (c₁, c₂) =mhʳ, gʳ) ( Enc (h; m, r) · Enc (h; n, t) = Enc (h; m · n, r + t) (mhʳ, gʳ) (nhᵗ, gᵗ)= (mnhʳ ⁺ᵗ, gʳ ⁺ᵗ) Componentwise multilication

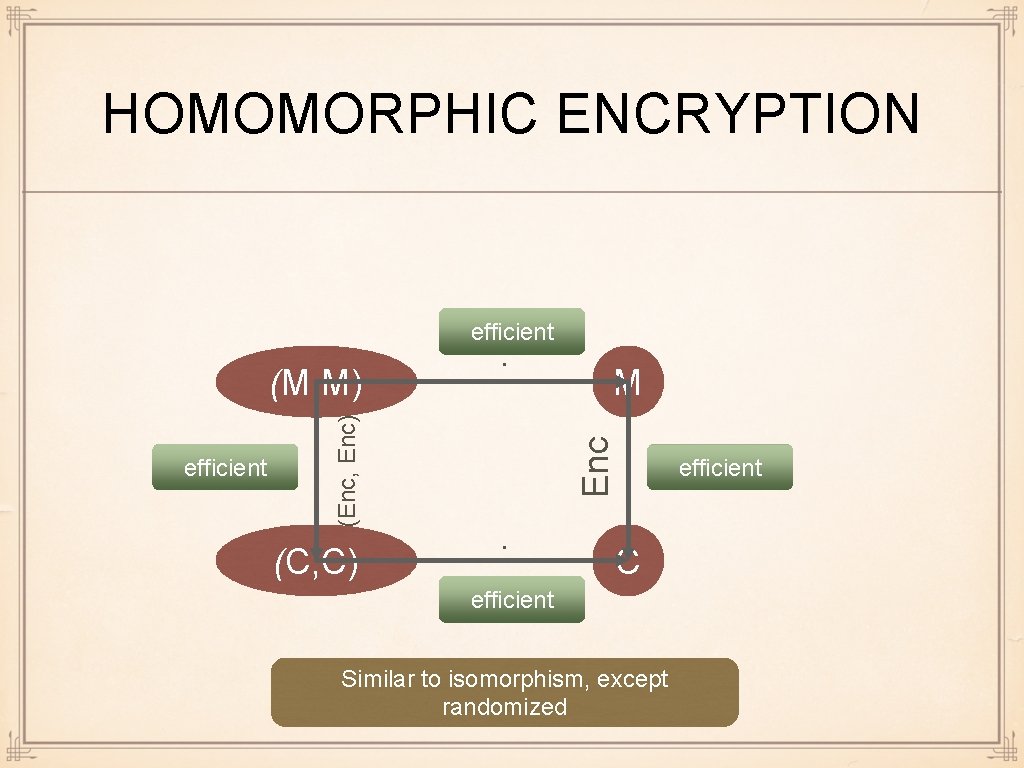
HOMOMORPHIC ENCRYPTION efficient (C, C) M Enc efficient (Enc, Enc) (M, M) · · C efficient Similar to isomorphism, except randomized efficient

SOME COROLLARIES Recall: Enc (m, r) · Enc (n, t) = Enc (m · n, r + t) We omit h (public key) for brevity in what follows 1. Πᵢ Enc (mᵢ; rᵢ) = Enc (Πᵢ mᵢ; Σᵢ rᵢ) 2. Enc (m, r)ˢ = Enc (mˢ, sr) for public s ∈ ℤq 3. Πᵢ Enc (x� ; rᵢ)^fᵢ = Πᵢ Enc ((x�)^ fᵢ; fᵢrᵢ) = Enc (Πᵢ (x�)^ fᵢ; Σᵢ fᵢrᵢ) Polynomials have a sum instead of product and product instead of exponentiation evaluating public "polynomial" at secret point

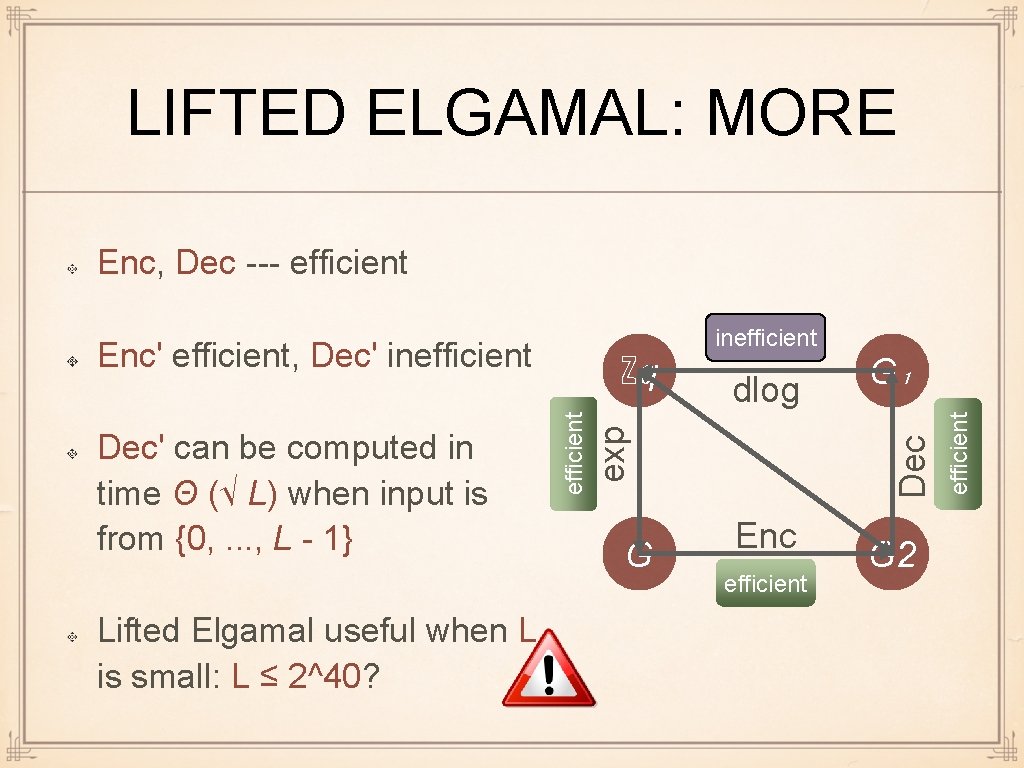
QUIZ: ENCRYPTING INTEGERS Elgamal makes it possible to encrypt group elements Question: how to encrypt (short) integers? Answer: Lifted Elgamal: use exponentiation (isomorphism) Enc' (m ∈ ℤq, r) = Enc (gᵐ, r) Dec' (c₁, c₂) = dlog g (Dec (c₁, c₂))

SOME COROLLARIES 1. Πᵢ Enc' (mᵢ; rᵢ) = Enc' (Σᵢ mᵢ; Σᵢ rᵢ) 2. Enc' (m, r)ˢ = Enc' (sm, sr) for public s ∈ ℤq 3. Πᵢ Enc' (x�; rᵢ)^fᵢ = Πᵢ Enc' (fᵢx�; fᵢrᵢ) = Enc' (Σᵢ fᵢx�; fᵢrᵢ) Σ� f (x) evaluation of public polynomial at secret point 4. Πᵢ Enc' (xᵢ; rᵢ)^yᵢ Enc'(z; t) = Enc' (Σᵢ xᵢ yᵢ + z; Σᵢ yᵢrᵢ + t) - arbitrary affine functions with public yᵢ, z

LIFTED ELGAMAL: MORE Enc, Dec --- efficient Lifted Elgamal useful when L is small: L ≤ 2^40? dlog exp efficient Dec' can be computed in time Θ (√ L) when input is from {0, . . . , L - 1} ℤq G G₁ Dec Enc' efficient, Dec' inefficient Enc efficient G 2 efficient inefficient

SUMMARY One can "compute" on Elgamal ciphertexts Plaintexts are group elements More useful: lifted Elgamal However, only efficient for small plaintexts limited malleability Secret computation of arbitrary affine functions in ℤq that have small outputs

STUDY OUTCOMES Secure computation: idea Modularization Elgamal IND-CPA security Malleability, homomorphic encryption Lifted Elgamal, its limitations

WHAT NEXT? Examples of concrete protocols quite cool non-trivial stuff can be done within given severe limitations Formalization and proof of their security