CRYPTOGRAPHIC PROTOCOLS 2015 LECTURE 13 Getting full zero

CRYPTOGRAPHIC PROTOCOLS 2015, LECTURE 13 Getting full zero knowledge helger lipmaa, university of tartu

UP TO NOW Introduction to the field Secure computation protocols Introduction to malicious model Σ-protocols

THIS TIME Σ-protocols: short reminder Constructing interactive zero knowledge protocols from Σ-protocols

REMINDER: Σ-PROTOCOLS x, ω 1 st message: commitment a x 2 nd message: challenge c 3 rd message: response z Requirement: c is chosen from publicly known challenge set C randomly. (Does not depend on a!) Terminology: public coin protocol Accepts iff prover knows ω such that (x, ω) ∈ R

REMINDER: Σ-PROTOCOLS x, ω 1 st message: commitment a x 2 nd message: challenge c 3 rd message: response z Accepts iff prover knows ω such that (x, ω) ∈ R 1. Completeness 2. Special Soundness 3. Special Honest-Verifier ZK (SHVZK)

RECALL: SEMIHONEST MODEL ω f x=Encoded(ω) Decode, obtain f (ω) Encoded(f(ω)) We know how to construct protocols for almost any task, that are secure under the assumption that Alice's input belongs to some public set S₁

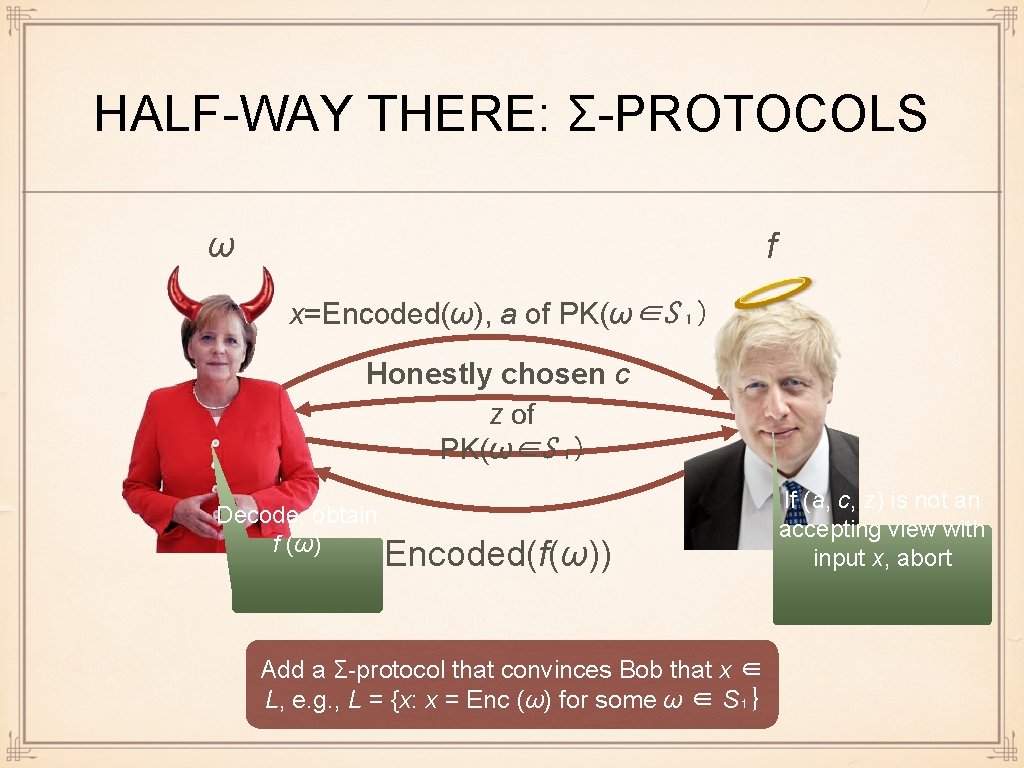
HALF-WAY THERE: Σ-PROTOCOLS ω f x=Encoded(ω), a of PK(ω∈S ₁) Honestly chosen c z of PK(ω∈S ₁) Decode, obtain f (ω) Encoded(f(ω)) Add a Σ-protocol that convinces Bob that x ∈ L, e. g. , L = {x: x = Enc (ω) for some ω ∈ S₁} If (a, c, z) is not an accepting view with input x, abort

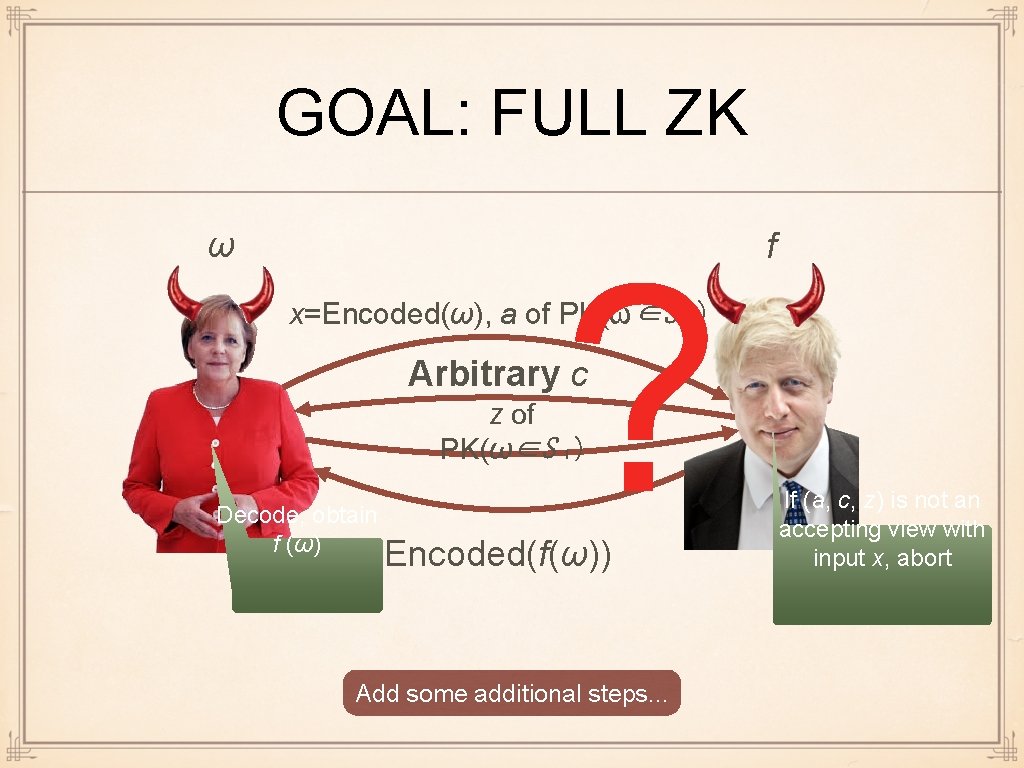
GOAL: FULL ZK ω ? f x=Encoded(ω), a of PK(ω∈S ₁) Arbitrary c z of PK(ω∈S ₁) Decode, obtain f (ω) Encoded(f(ω)) Add some additional steps. . . If (a, c, z) is not an accepting view with input x, abort

BASIC IDEA x, ω 1 st message: commitment a x 2 nd message: challenge c 3 rd message: response z Accepts iff prover knows ω such that (x, ω) ∈ R Σ-protocol is only zero knowledge when c is completely random. This is since we start simulating by picking c randomly, and then choose (z, a). It suffices for c to be independent of a: Bob's best strategy is then to guess c Goal: guarantee c is independent of a

QUIZ: HOW? Question: how to guarantee a and c are mutually independent? Hint: Internet is asynchronous, so one message (say c) must be sent first, but in a "hidden" form Content only revealed after second message (say a) is sent

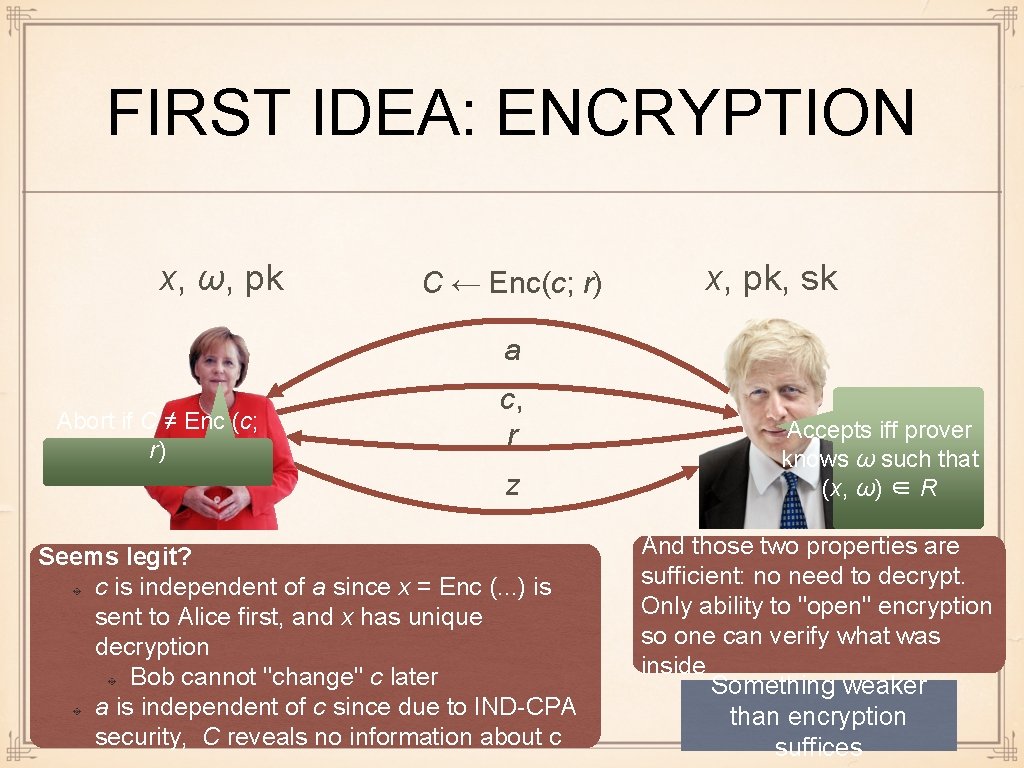
FIRST IDEA: ENCRYPTION x, ω, pk C ← Enc(c; r) x, pk, sk a Abort if C ≠ Enc (c; r) c, r z Seems legit? c is independent of a since x = Enc (. . . ) is sent to Alice first, and x has unique decryption Bob cannot "change" c later a is independent of c since due to IND-CPA security, C reveals no information about c Accepts iff prover knows ω such that (x, ω) ∈ R And those two properties are sufficient: no need to decrypt. Only ability to "open" encryption so one can verify what was inside Something weaker than encryption suffices

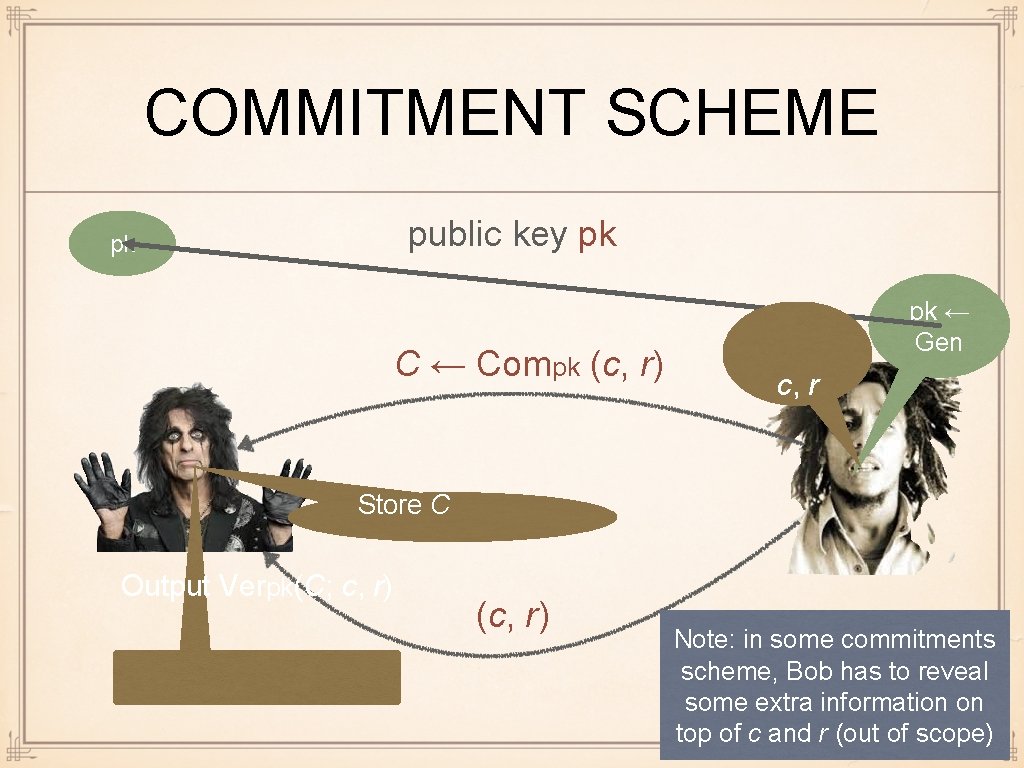
COMMITMENT SCHEME A commitment scheme consists of three algorithms: key generation Gen (. . . ) → pk commitment Compk (c; r) → C verification algorithm Verpk (C; c, r)∈{0, 1} We saw what was essentially a commitment scheme in the case of Hamiltonean Path

COMMITMENT SCHEME public key pk pk C ← Compk (c, r) pk ← Gen c, r Store C Output Verpk(C; c, r) (c, r) Note: in some commitments scheme, Bob has to reveal some extra information on top of c and r (out of scope)

SECURITY GOALS OF COMMITMENT Computational hiding (IND-CPA): given c₀, c₁, pk and C = Compk (cb, r), it is difficult to guess b Perfect binding: for every C, there exists at most one c such that C = Compk (c, ·) for some r

IND-CPA PKC = PH COMMITMENT Theorem. Every IND-CPA secure cryptosystem is a perfectly binding and computationally hiding commitment scheme Proof. Obvious: perfect binding follows from unique decryption computational hiding follows from IND-CPA security

REFINED: PH COMMITMENT x, ω, pk C ← Com(c; r) x, pk a Abort if Ver(C, c, r)=0 c, r z Seems legit? c is independent of a since C = Com (c, r) is sent to Alice first, and Com is perfectly binding Bob cannot open C to something different a is independent of c since due to IND-CPA security, C reveals no information about c Accepts iff prover knows ω such that (x, ω) ∈ R Can you find a problem?

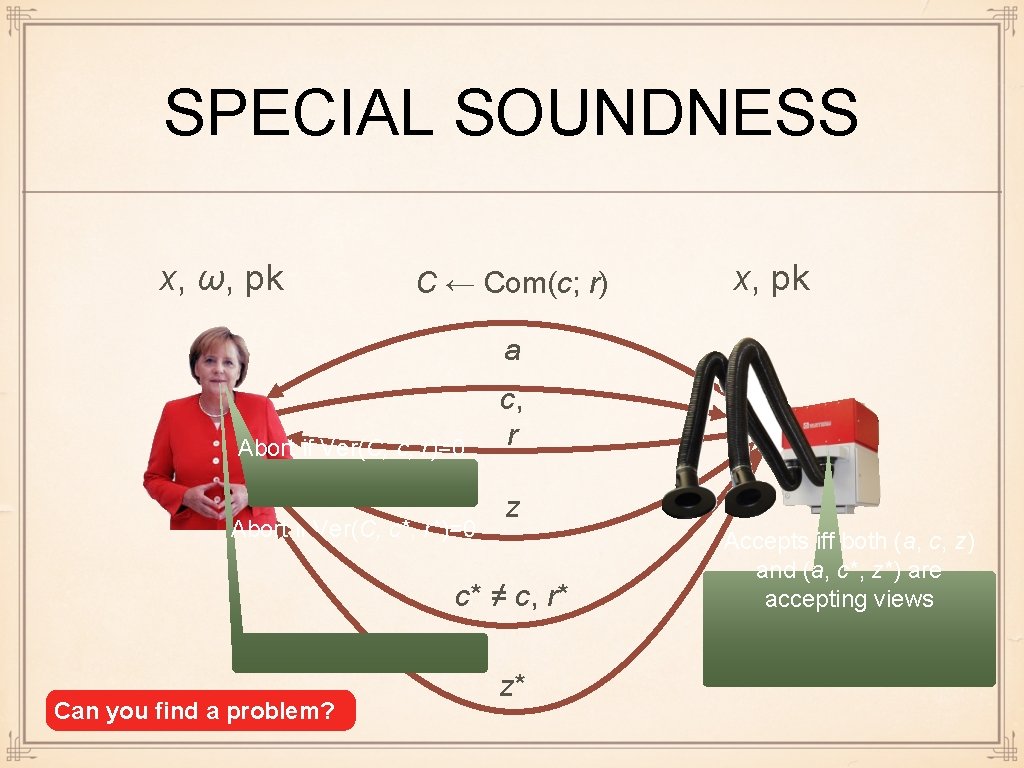
SPECIAL SOUNDNESS x, ω, pk C ← Com(c; r) x, pk a Abort if Ver(C, c, r)=0 Abort if Ver(C, c*, r*)=0 c, r z c* ≠ c, r* Can you find a problem? z* Accepts iff both (a, c, z) and (a, c*, z*) are accepting views

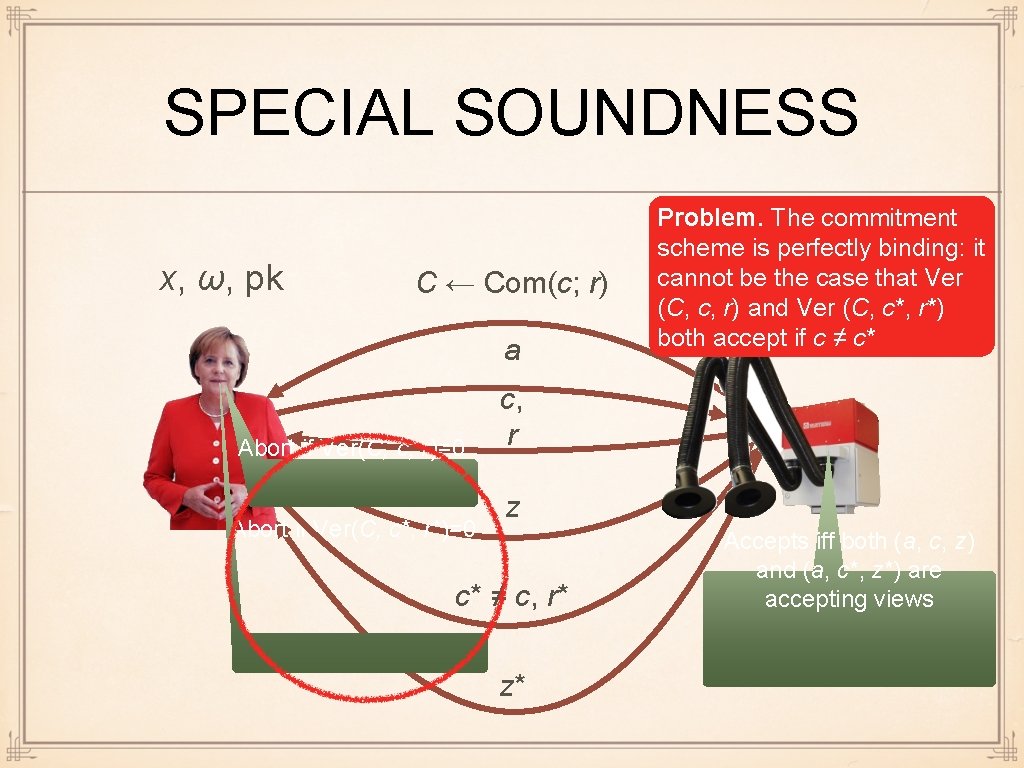
SPECIAL SOUNDNESS x, ω, pk C ← Com(c; r) a Abort if Ver(C, c, r)=0 Abort if Ver(C, c*, r*)=0 Problem. The commitment scheme is perfectly binding: it cannot x, be pk the case that Ver (C, c, r) and Ver (C, c*, r*) both accept if c ≠ c* c, r z c* ≠ c, r* z* Accepts iff both (a, c, z) and (a, c*, z*) are accepting views

QUIZ: SOLUTION? Question: what do do? Hint 1: commitment scheme should not be perfectly binding For every c ≠ c*, r there should exist r*, such that Com (c, r) = Com (c*, r*) Hint 2: finding such collusions should be easy for extractor, but difficult for a (malicious/honest) verifier We need (trapdoor) computational binding, where binding can be broken by a party who knows some "trapdoor"

TRAPDOOR COMMITMENT Perfect hiding: Distribution of Com (pk; m, r) does not depend on m Computational binding: for every C, m, r, m* ≠ m, without knowing trapdoor sk, it is computationally hard to find r*, such that C = Com (pk; m, r) = Com (pk; m*, r*) Trapdoor: given sk, m, r, m* ≠ m, it is computationally easy to find r* such that Com (pk; m, r) = Com (pk; m*, r*)

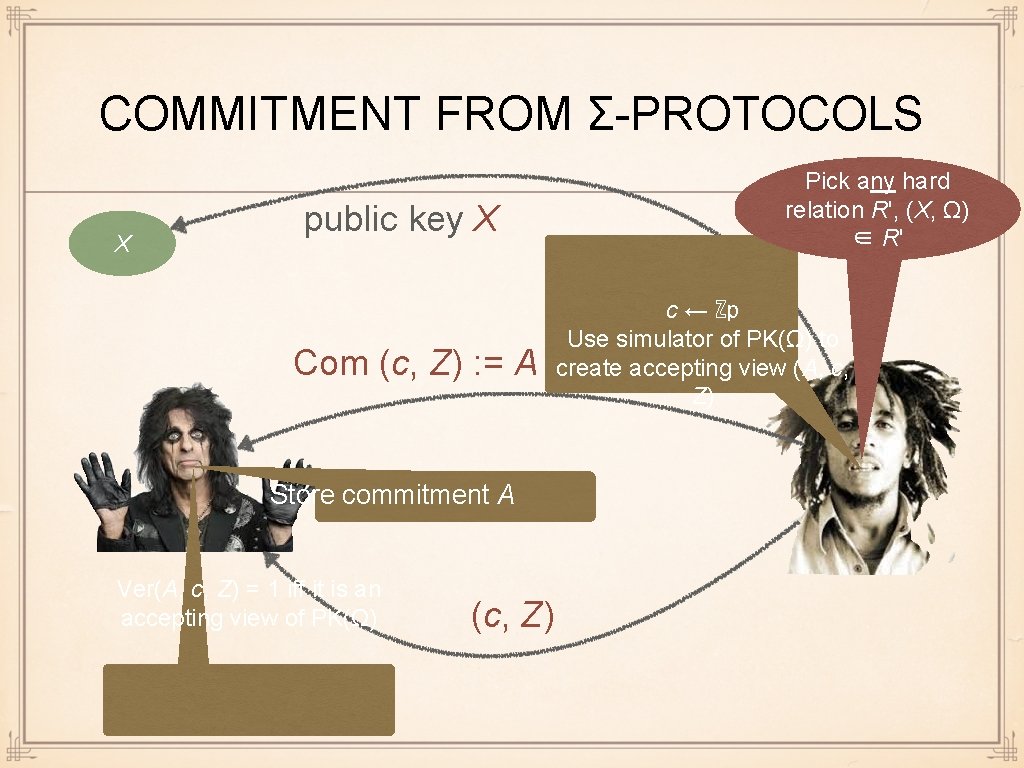
CHOICE OF COMMITMENT SCHEME We use a commitment scheme that is constructed from any Σ-protocol for any hard language We use the fact that in the final protocol we only need to commit to random messages The committed message = c of original protocol We use this commitment scheme since it fits well our goals: it has more than one usage

COMMITMENT FROM Σ-PROTOCOLS X public key X Com (c, Z) : = A Store commitment A Ver(A, c, Z) = 1 iff it is an accepting view of PK(Ω) (c, Z) Pick any hard relation R', (X, Ω) ∈ R' c ← ℤp Use simulator of PK(Ω) to create accepting view (A, c, Z)

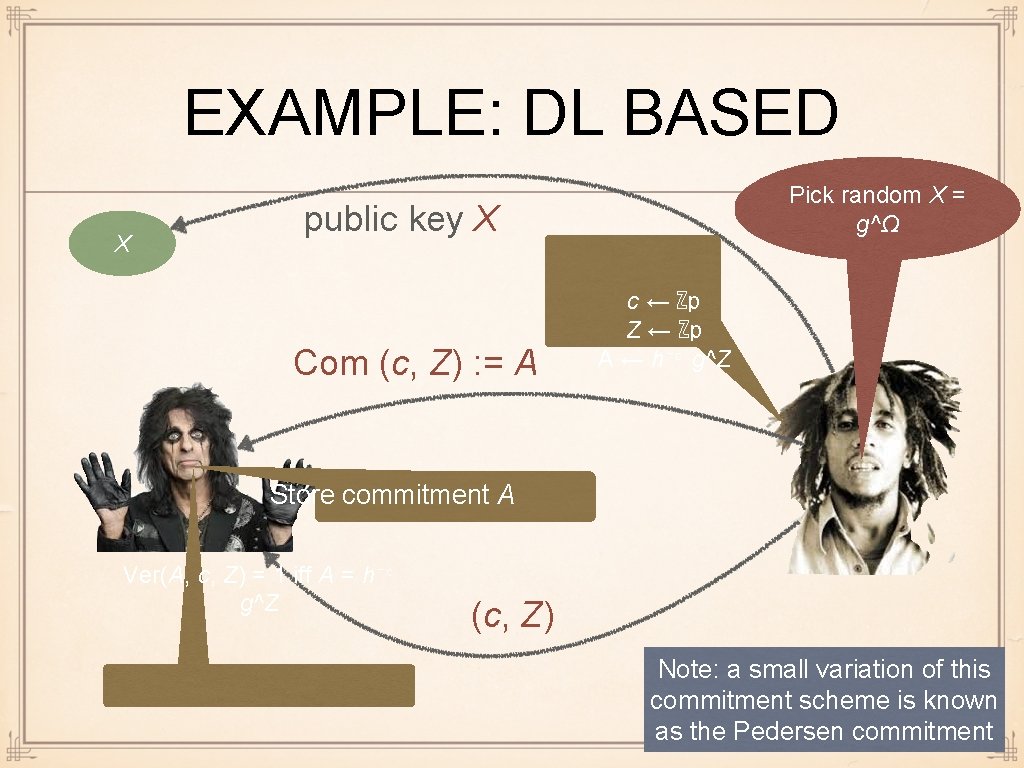
EXAMPLE: DL BASED X Pick random X = g^Ω public key X Com (c, Z) : = A c ← ℤp Z ← ℤp A ← h⁻ᶜ g^Z Store commitment A Ver(A, c, Z) = 1 iff A = h⁻ᶜ g^Z (c, Z) Note: a small variation of this commitment scheme is known as the Pedersen commitment

SECURITY OF THIS COMMITMENT Theorem. The commitment scheme of the last slide is computationally binding (if R' is hard), perfectly hiding, and trapdoor specially sound => computational binding: assume adversary outputs (A, c, Z), (A, c*, Z*), c ≠ c*, such that both accept. But then we can use extractor to recover Ω, thus R' is not hard SHVZK => perfect hiding: follows since in real protocol, A is randomly chosen before c is chosen, and real protocol and simulator are indistinguishable Completeness => trapdoor: given Ω, one can start Σ-protocol with any A, and then find Z corresponding to any c such that (A, c, Z) is accepting

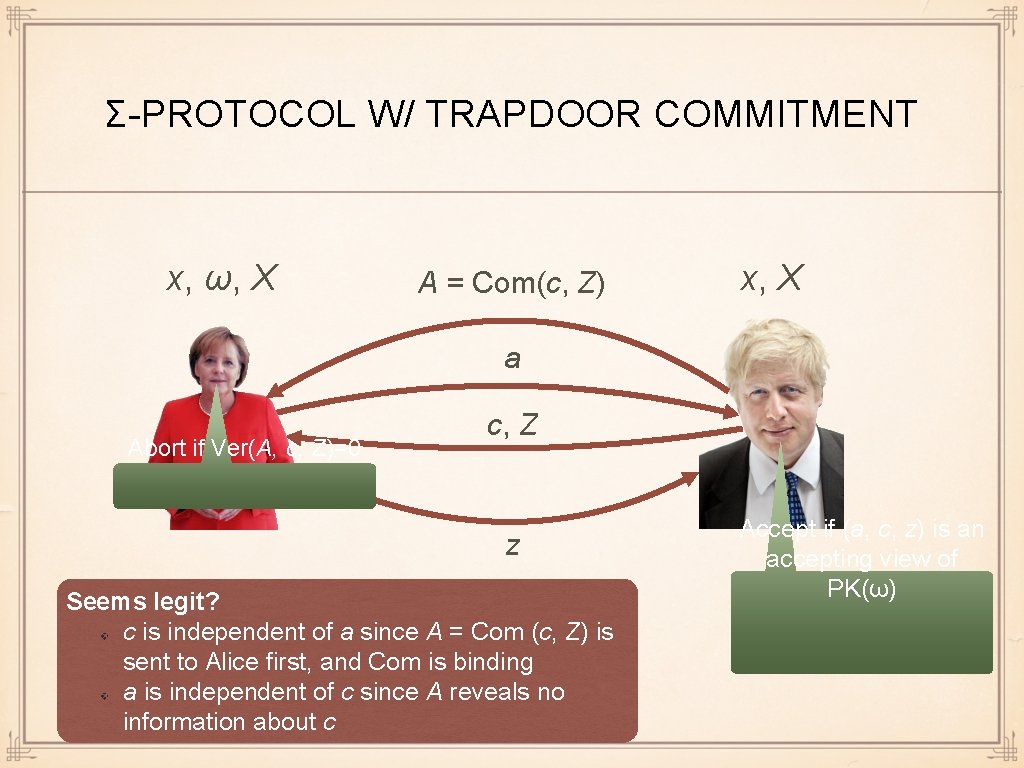
Σ-PROTOCOL W/ TRAPDOOR COMMITMENT x, ω, X A = Com(c, Z) x, X a Abort if Ver(A, c, Z)=0 c, Z z Seems legit? c is independent of a since A = Com (c, Z) is sent to Alice first, and Com is binding a is independent of c since A reveals no information about c Accept if (a, c, z) is an accepting view of PK(ω)

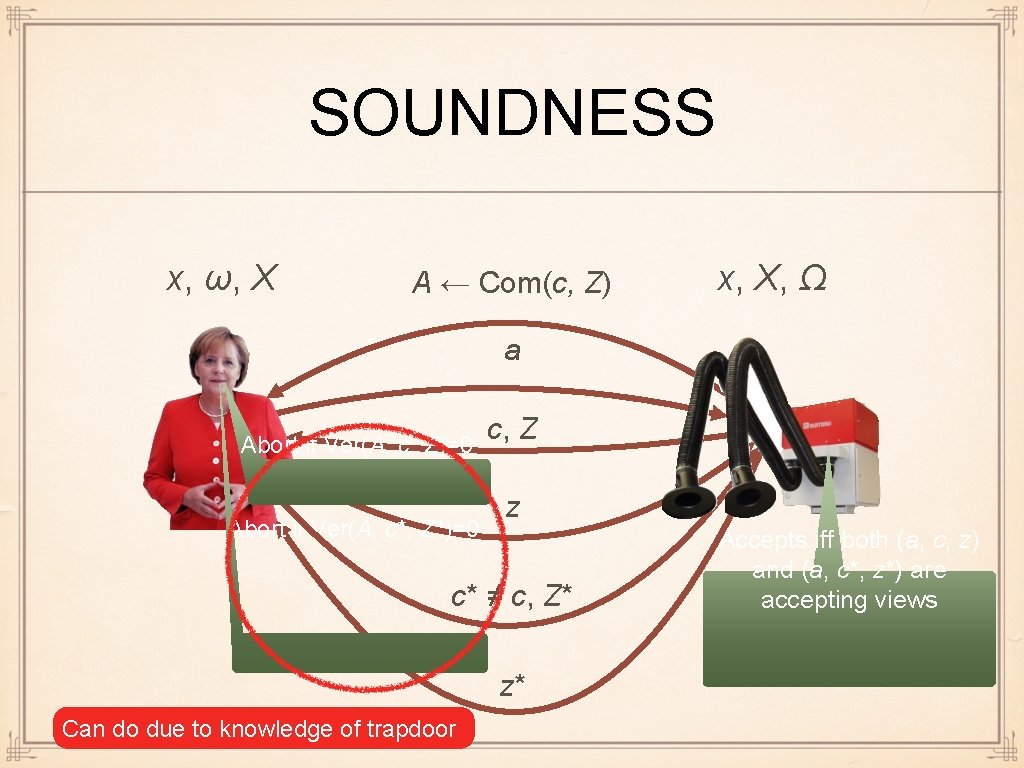
SOUNDNESS x, ω, X A ← Com(c, Z) x, X, Ω a Abort if Ver(A, c, Z)=0 Abort if Ver(A, c*, Z*)=0 c, Z z c* ≠ c, Z* z* Can do due to knowledge of trapdoor Accepts iff both (a, c, z) and (a, c*, z*) are accepting views

QUIZ: ARE WE DONE? Guess: are we done? Answer: we checked: soundness is ok but what about ZK? let's check. . . (not done)

BASIC IDEA x, ω 1 st message: commitment a x 2 nd message: challenge c 3 rd message: response z Goal: guarantee c is independent of a Accepts iff prover knows ω such that (x, ω) ∈ R

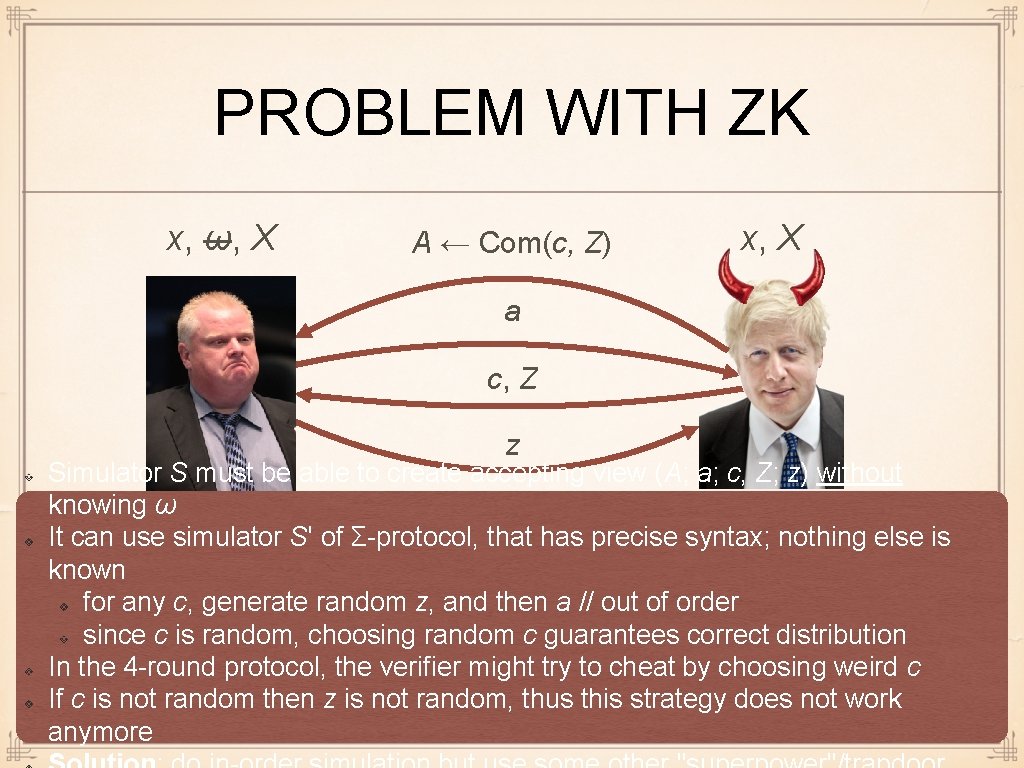
PROBLEM WITH ZK x, ω, X A ← Com(c, Z) x, X a c, Z z Simulator S must be able to create accepting view (A; a; c, Z; z) without knowing ω It can use simulator S' of Σ-protocol, that has precise syntax; nothing else is known for any c, generate random z, and then a // out of order since c is random, choosing random c guarantees correct distribution In the 4 -round protocol, the verifier might try to cheat by choosing weird c If c is not random then z is not random, thus this strategy does not work anymore

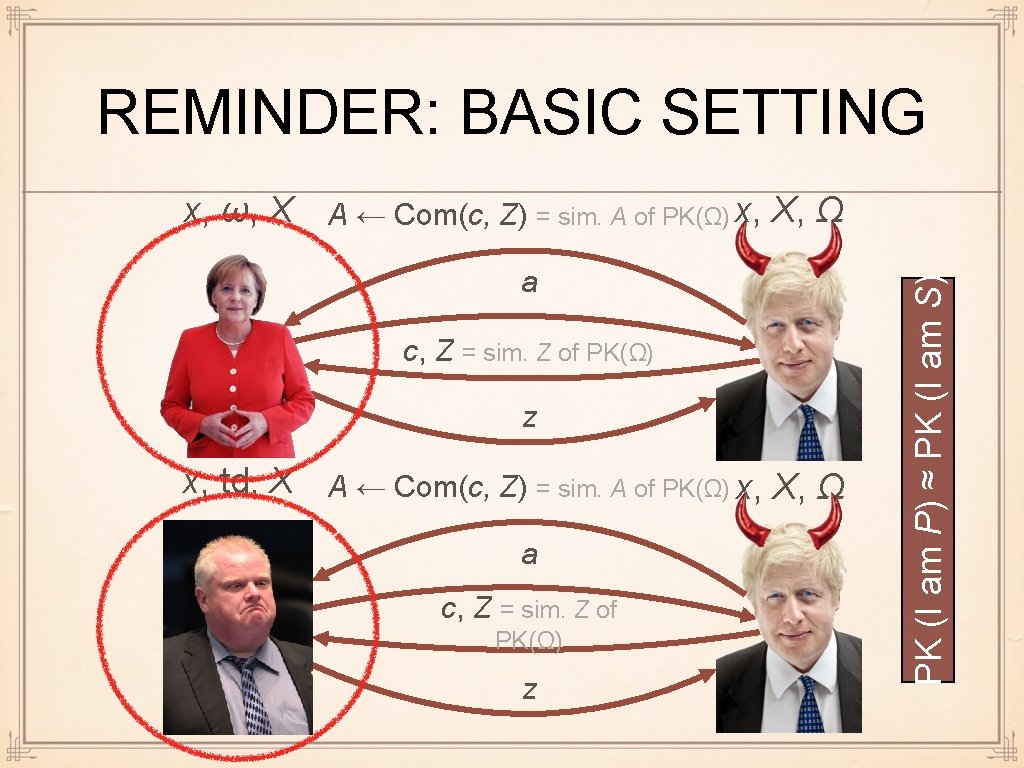
REMINDER: BASIC SETTING a c, Z = sim. Z of PK(Ω) z x, td, X A ← Com(c, Z) = sim. A of PK(Ω) x, X, Ω a c, Z = sim. Z of PK(Ω) z PK (I am P) ≈ PK (I am S) x, ω, X A ← Com(c, Z) = sim. A of PK(Ω) x, X, Ω

IDEA: PK (I AM P OR S) C ← Com(c, Z) x, X, Ω a of PK (ω ∨ Ω) c, Z z of PK (ω ∨ Ω) X, x, Ω A ← Com(c, Z) a of PK (ω ∨ Ω) c, Z z of PK (ω ∨ Ω) x, X, Ω Really are indistinguishable X, x, ω

IDEA Let V create (X, Ω) ∈ R', and send X to P with her first message Quiz: how can simulator obtain Ω from V? Answer: we let V to prove the knowledge of Ω to P Simulator of ZK protocol uses extractor of Σprotocol to extract Ω from V

4 -ROUND ZERO KNOWLEDGE X, A of PK(Ω) x, ω x, new (X, Ω) a of PK (ω ∨ Ω), C of PK(Ω) Z of PK(Ω), c of PK (ω ∨ Ω) Abort if Ver(A, C, Z)=0 Accepts if (a, c, z) is accepting view of PK (ω ∨ Ω) since X is used once, it does not matter if information about it leaks, thus PK(Ω) can be HVZK z of PK (ω ∨ Ω) superpower: rewinding again

SECURITY OF 4 -ROUND PROTOCOL Theorem. Assume Σ-protocols for PK(ω) and PK(Ω) are complete, specially sound and SHVZK for language L and language L'. Assume L' is a hard language. Then the protocol from the previous slide is a computationally sound and perfectly zero knowledge 4 -round proof for L. ZK: Simulator uses extractor of PK (Ω) to obtain Ω and then executes PK (ω ∨ Ω) superpower: using rewinding in simulation comp. sound: Assume prover succeeds in convincing verifier. Then we can use extractor to either extract ω or Ω from P. But since L' is a hard language, P knows Ω only with a negligible probability

REMARKS Important: V can use any hard language L' just choose L' that suits the rest of ZK proof is about graphs, use GI, etc. . . or just use something efficient (knowledge of DL)

REMARK ON COMMITMENT SCHEME We chose the concrete commitment scheme so that at the last step the number of modifications would be minimal There are many other commitment schemes available

JUNGLE OF INTERACTIVE ZK Zero-knowledge has many parameters Plain model, CRS model, random oracle model, bare public key model main problem: if several proofs are run in parallel, a Standalone/concurrent/UC message of one proof can be used in another proof. How to construct simulatable proofs becomes major hurdle Resettable Computational or perfect soundness. . . you do not have to remember those notions, it's a jungle

NIZK: ZK proof is a bit string Verification can be done without interaction with prover Many verifiers verify the same proof whenever they need Example: e-voting, P = voter, NIZK V =is what voting we need in practice server since we cannot interleave messages from different proofs: every proof is one message Bonus: no problems with concurrency, . . .

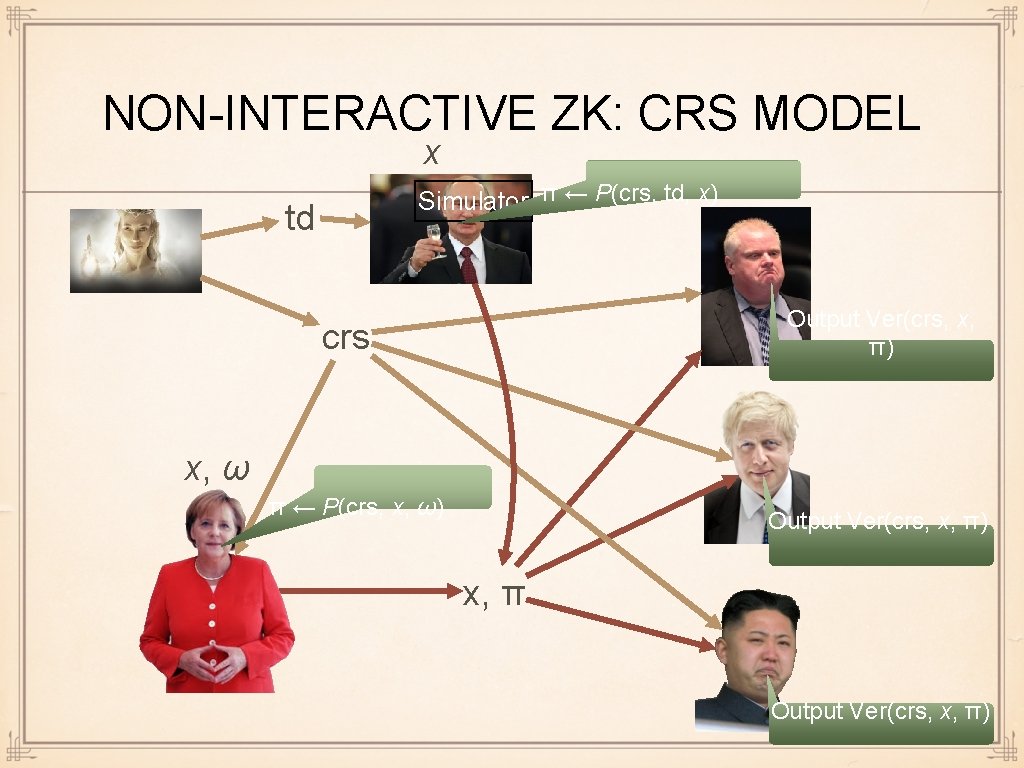
CRS MODEL Recall: simulator needs some extra power otherwise contradicts soundness Interactive ZK: superpower = rewinding Non-interactive ZK: cannot rewind, need some other extra power

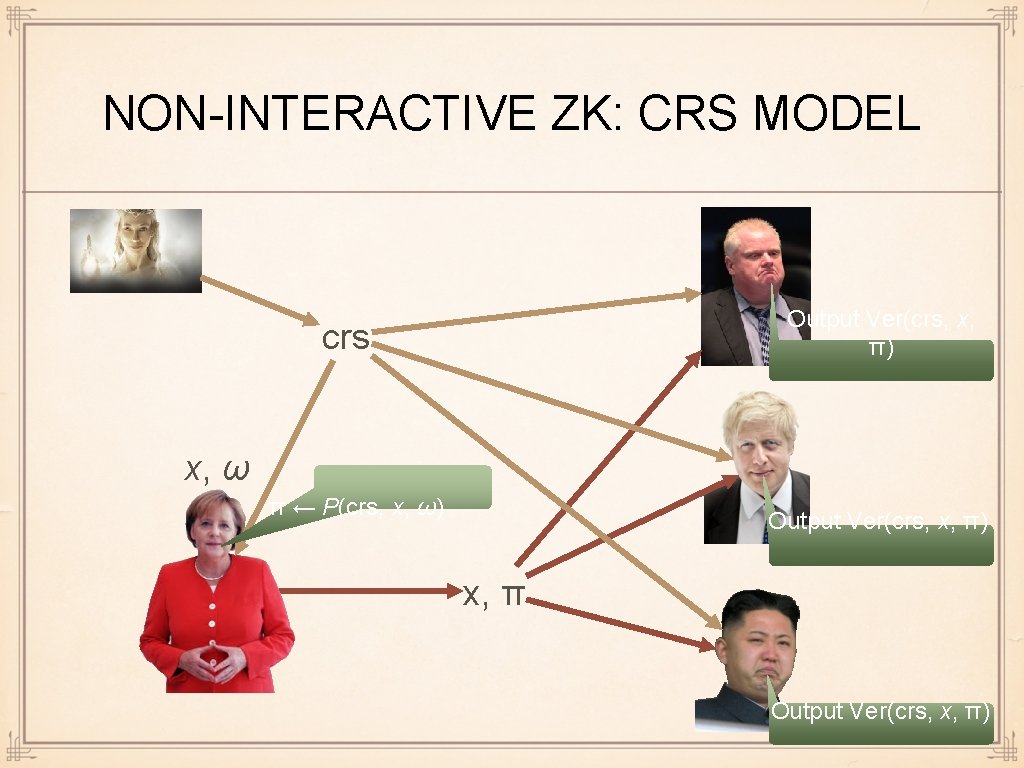
NON-INTERACTIVE ZK: CRS MODEL Output Ver(crs, x, π) crs x, ω π ← P(crs, x, ω) Output Ver(crs, x, π) x, π Output Ver(crs, x, π)

NON-INTERACTIVE ZK: CRS MODEL x Simulator π ← P(crs, td, x) td Output Ver(crs, x, π) crs x, ω π ← P(crs, x, ω) Output Ver(crs, x, π) x, π Output Ver(crs, x, π)

NIZK IN CRS MODEL Quite a few efficient methodologies to construct NIZK in CRS model are known Most of them use "pairings" Will talk about pairings in the last 2 lectures

STUDY OUTCOMES Getting full ZK from Σ-protocols Getting soundness - via commitment schemes Getting ZK - via OR proof and additional Σ-protocol We can now construct ZK for any language in NP hence do crypto in malicious model. . . though not necessarily efficiently

NEXT LECTURE We are "done" with showing one can in principle compute anything in malicious model Last lectures: some specific tools to get better efficiency Next lecture: garbled circuits very good computation, rounds bad communication