CRYPTOGRAPHIC PROTOCOLS 2015 LECTURE 16 GrothSahai proofs helger

CRYPTOGRAPHIC PROTOCOLS 2015, LECTURE 16 Groth-Sahai proofs helger lipmaa, university of tartu

UP TO NOW Introduction to the field Secure computation protocols Interactive zero knowledge from Σ-protocols Pairing-based cryptography

THIS TIME Pairing-based ZK in the CRS model Simple examples An example of Groth-Sahai proofs: efficient NIZK proofs for algebraic relations

ADDITIVE NOTATION Additive notation for group op-s / pairings We denote group elements in bold Group operation: g + h (instead of gh) Exponentiation: a · g (instead of ga) We still denote opposite of this by log: logg ag = a Pairing: see the next slide Makes it easier to read, since we have many things in exponents plus it will make sense from algebraic viewpoint although it is probably confusing : (

REMINDER: PAIRINGS Pairing: function ê: G 1 × G 2 → G' that satisfies all three groups have order p, pairing is symmetric if G 1 = G 2 =: G, otherwise asymmetric Bilinearity: ê (ag₁, bg₂) = ab · ê (g 1, g 2) Non-degenerative: ê (ag 1, bg 2) ≠ 0 if a, b ≠ 0, gi ≠ 0 Efficiently computable κ) returns (p, G × G , G', ê) Setup (1 1 2 Basic fact of pairings: ê (ag 1, bg 2) = ê (cg 1, dg 2) <=> ab = cd

COMPONENT-WISE NOTATION We also use a lot of component-wise notation a(g, h) = (ag, ah) (a, b)g = (ag, bg) // symmetric pairings ê ((A, B), (C, D)) = (ê (A, C), ê (B, D))

GROTH-SAHAI PROOFS Let Com be some well-defined commitment scheme Goal (general): Given Ai = Com (ai), verify that various algebraic equations hold between ai ai can be either group element (ai) or exponent Example goal: for Ai = Com(ai), Bi = Com(bi), it holds that C = Com (Σbiai)

GROTH-SAHAI PROOFS Only hardness assumption: The commitment scheme is secure Several instantiations known (XDH, DLIN, . . . ) Variant 0: Com is perfectly binding/comp. hiding Perfectly sound/computationally NIZK Variant 1: Com is comp. binding/perfectly hiding Computationally sound/perfectly NIZK

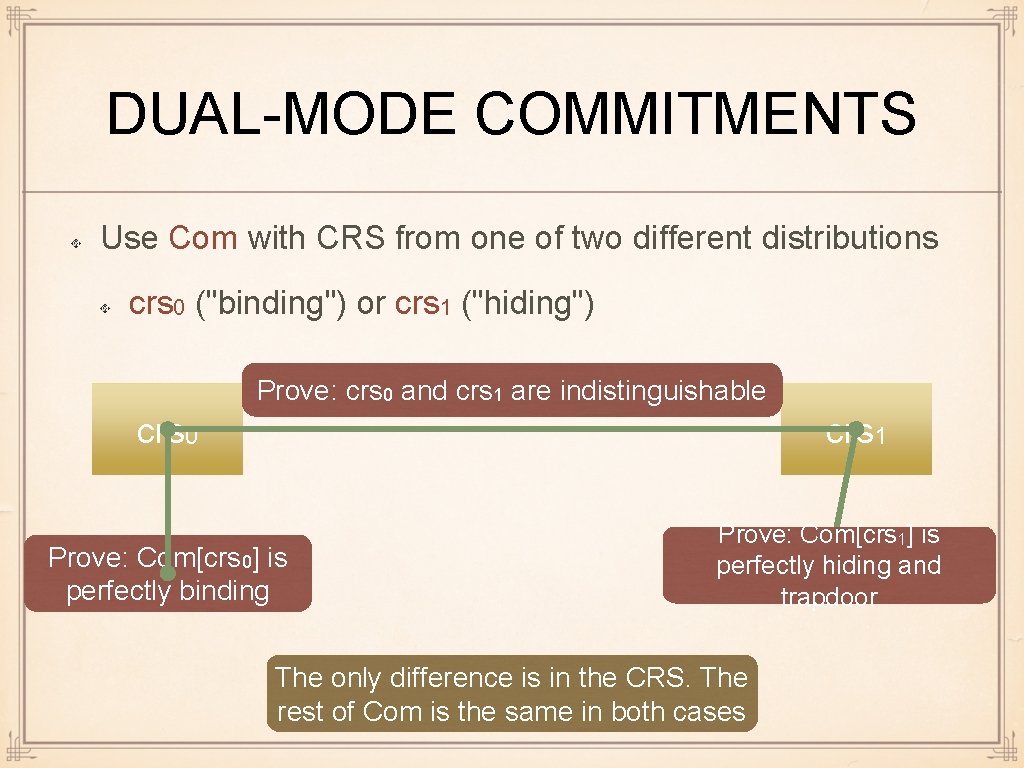
DUAL-MODE COMMITMENTS Use Com with CRS from one of two different distributions crs 0 ("binding") or crs 1 ("hiding") Prove: crs 0 and crs 1 are indistinguishable crs 0 crs 1 Prove: Com[crs 0] is perfectly binding Prove: Com[crs 1] is perfectly hiding and trapdoor The only difference is in the CRS. The rest of Com is the same in both cases

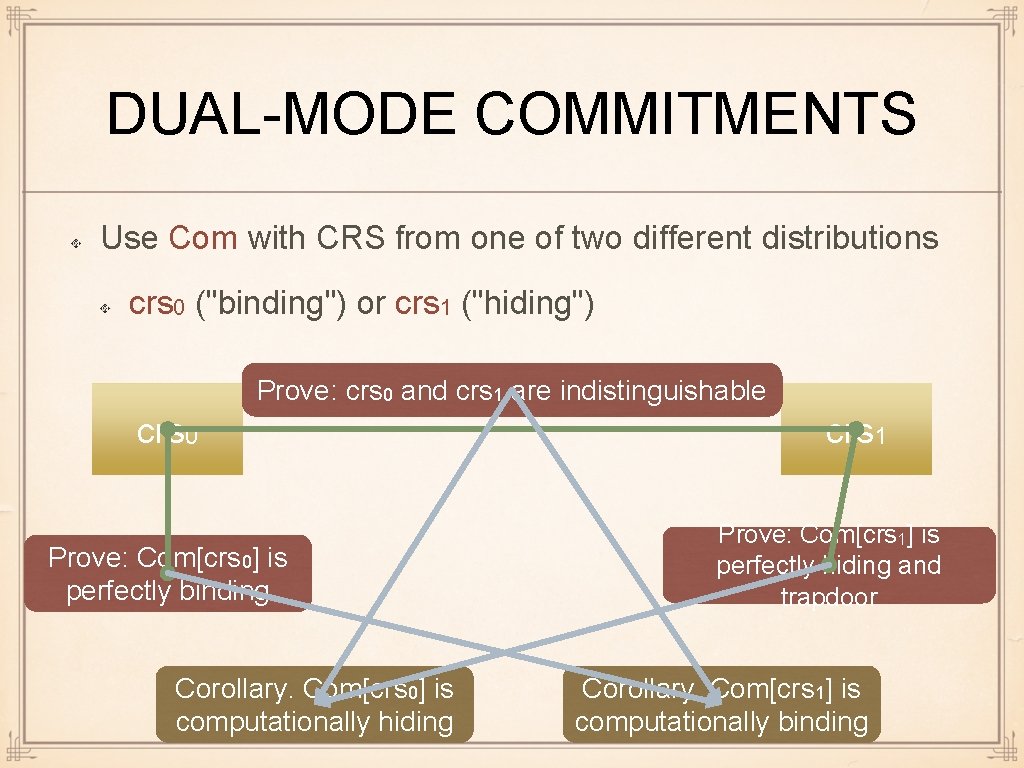
DUAL-MODE COMMITMENTS Use Com with CRS from one of two different distributions crs 0 ("binding") or crs 1 ("hiding") Prove: crs 0 and crs 1 are indistinguishable crs 0 Prove: Com[crs 0] is perfectly binding Corollary. Com[crs 0] is computationally hiding crs 1 Prove: Com[crs 1] is perfectly hiding and trapdoor Corollary. Com[crs 1] is computationally binding

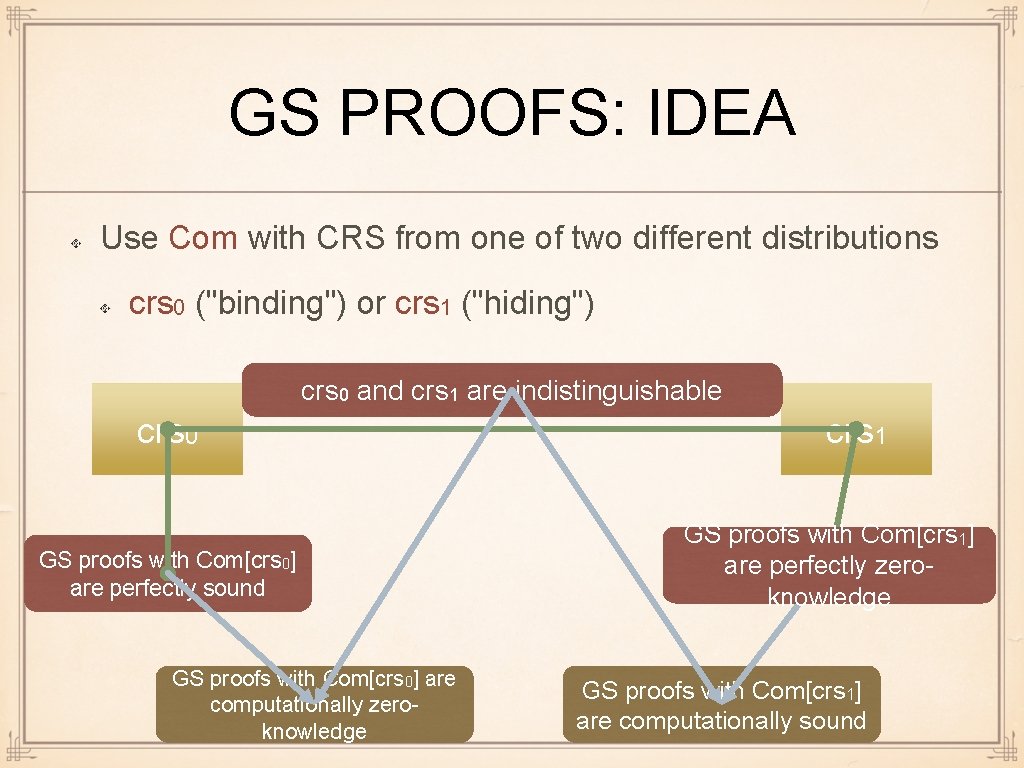
GS PROOFS: IDEA Use Com with CRS from one of two different distributions crs 0 ("binding") or crs 1 ("hiding") crs 0 and crs 1 are indistinguishable crs 0 GS proofs with Com[crs 0] are perfectly sound GS proofs with Com[crs 0] are computationally zeroknowledge crs 1 GS proofs with Com[crs 1] are perfectly zeroknowledge GS proofs with Com[crs 1] are computationally sound

DMC: TECHNICALITIES We need two separate commitment schemes: DMCG, to commit to group elements and DMCE, to commit to exponents DMCG and DMCE have to play well together Due to this and DMC requirements, DMCG/DMCE are somewhat complicated

DIFFERENT INSTANTIATIONS Different instantiations of DMCE/DMCG are known based on say XDH, DLIN, SH assumptions We will describe DMCE/GS proof with XDH thus we need to use asymmetric pairings Will not have time to describe DMCG, DLIN/SH setting proofs, . . .

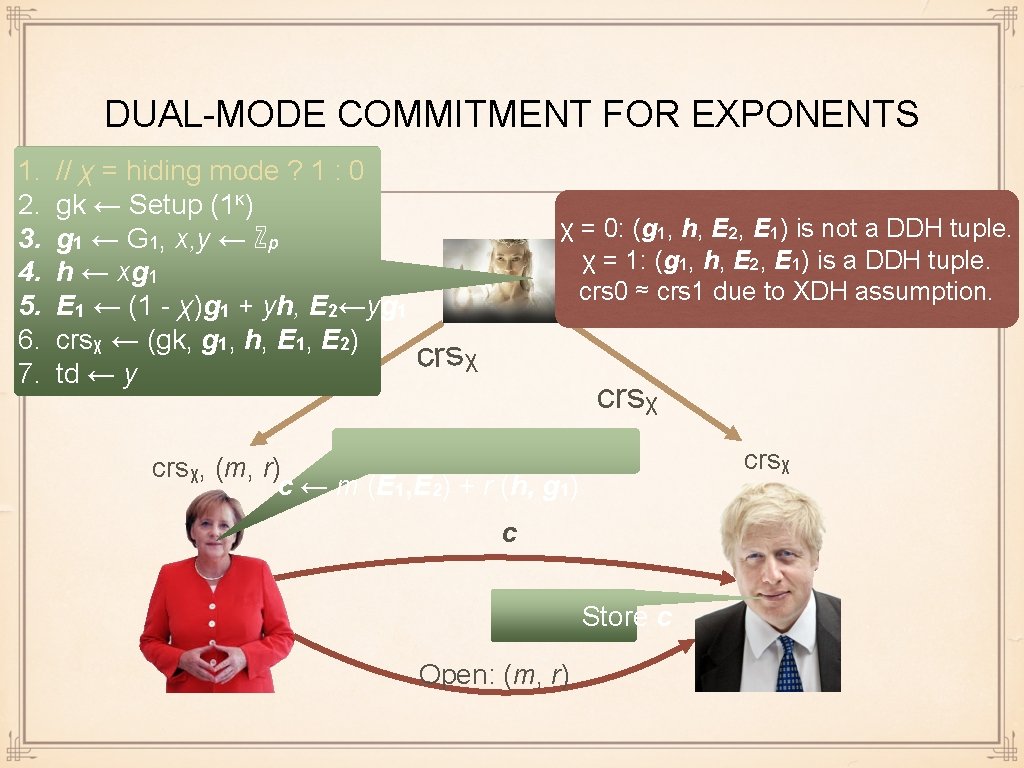
DMCE: IDEA We need to create crs 0 and crs 1 that are computationally indistinguishable under XDH Idea: let crsχ = (gk, g 1, h, E 1, E 2), where (g 1, h, E 2, E 1) is not a DDH tuple if χ = 0 indistinguishable under XDH assumption (g 1, h, E 2, E 1) is a DDH tuple if χ = 1

DUAL-MODE COMMITMENT FOR EXPONENTS 1. 2. 3. 4. 5. 6. 7. // χ = hiding mode ? 1 : 0 gk ← Setup (1κ) g 1 ← G 1, x, y ← ℤp h ← xg 1 E 1 ← (1 - χ)g 1 + yh, E 2←yg 1 crsχ ← (gk, g 1, h, E 1, E 2) td ← y χ = 0: (g 1, h, E 2, E 1) is not a DDH tuple. χ = 1: (g 1, h, E 2, E 1) is a DDH tuple. crs 0 ≈ crs 1 due to XDH assumption. crsχ, (m, r) c ← m (E 1, E 2) + r (h, g 1) c Store c Open: (m, r)

PERFECT BINDING WITH CRS 0 crs 0 = (gk, g 1, h = xg 1, E 1 ← g 1 + yh, E 2 ← yg 1) Com (m; r) = m (E 1, E 2) + r (h, g 1) = (mg 1 + (my + r)h, (my + r)g 1) = Elgamal (m; my + r) // r is random Thus perfectly binding and computationally hiding

PERFECT HIDING WITH CRS 1 crs 1 = (gk, g 1, h = xg 1, E₁ ← 0 g 1 + yh, E 2 ← yg 1) Com (m; r) = m (E₁ + E 2) + r(h, g 1) = (my + r)(h, g 1) ≈ random DDH tuple Perfectly hiding since r is random Since crs 0 ≈ crs 1, and DMCE[crs 0] is perfectly binding => this version is computationally binding under XDH

TRAPDOOR WITH CRS 1 crs 1 = (gk, g 1, h = xg 1, E₁ ← yh, E 2 ← yg 1) Com (m; r) = m (E₁ + E 2) + r(h, g 1) = (my + r)(h, g 1) Set td ← y Given m*, compute r* such that my + r = m*y + r* Com (m*; r*) = (m*y + r*) (h, g 1) = (my + r) (h, g 1) = Com (m; r) Clearly trapdoor

DMCE SECURITY: THEOREM Theorem. Assume XDH holds. DMCE is either perfectly binding and computationally hiding (if crs 0 is used), or computationally binding, perfectly hiding, and trapdoor (if crs 1 is used). Proof. Given on previous pages.

FIRST GROTH-SAHAI PROOF Goal: Given Zi = Com (zi; ri) ∈ G 12 and Ai, T ∈ G 2 Construct NIZK proof that ∑ zi. Ai = T Denote (A, B) ● C : = (ê (A, C), ê (B, C)) The first argument of ● is a commitment ∈ G 12

FIRST GROTH-SAHAI PROOF Goal: prove that ∑ zi · Ai = 1 · T, given Zi = Com(zi; ri), Ai, T The basic idea is always similar Use commitments instead of messages, and additions/bilinear operations in different algebraic domain show that if randomness is zero then ∑ (Com (zi; 0) ● Ai) = Com (1; 0) ● T Both · and ● are bilinear operations For any randomness: to prove ∑zi Ai = T, derive π ∈ G 2 from ∑ (Com (zi; ri) ● Ai) = Com (1; 0) ● T + Ê (. . . , π) order important: asymmetric pairings π compensates for added randomness

VERIFICATION WITHOUT PRIVACY First, consider the case without privacy Zi = Com(zi; 0) = zi (E 1, E 2) + 0 (h, g 1) Com (1; 0) = (E 1, E 2) ∑ (Com(zi; 0) ● Ai) = ∑ (zi (E 1, E 2) ● Ai) = (E 1, E 2) ● (∑ zi Ai) = (E 1, E 2) ● T Thus ∑ (Com (zi; 0) ● Ai) = Com (1; 0) ● T

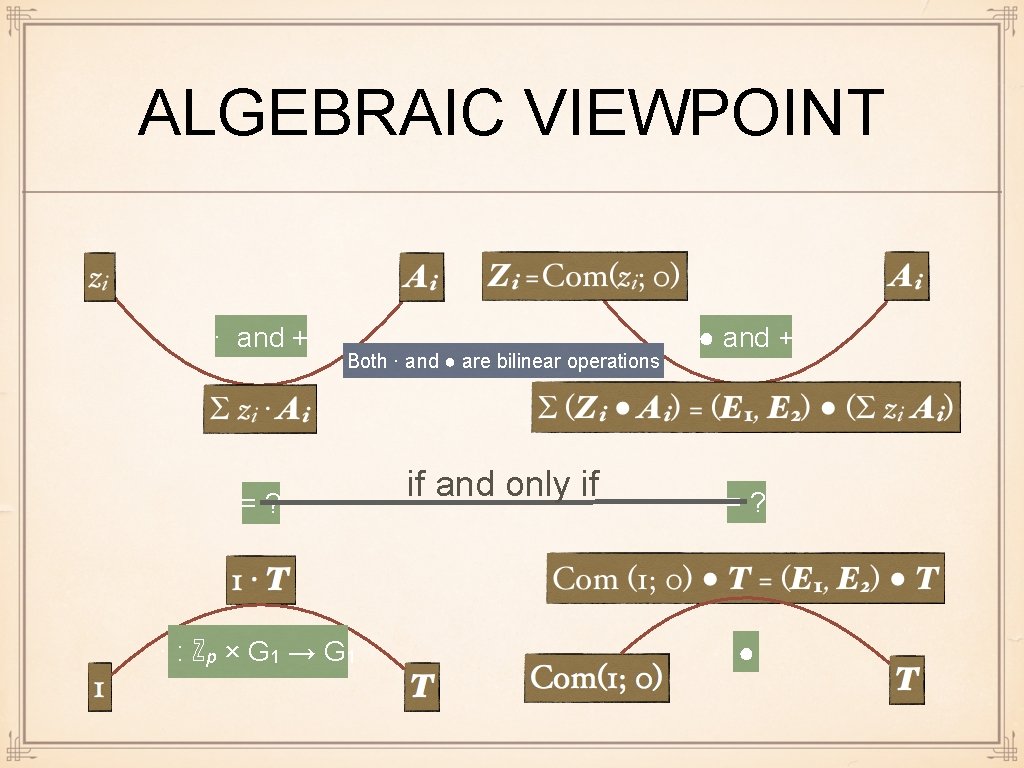
ALGEBRAIC VIEWPOINT · and + Both · and ● are bilinear operations =? · : ℤp × G 1 → G 1 if and only if ● and + =? ●

GENERAL CASE WITH RANDOMNESS Recall: crsχ = (gk, g 1, h ← xg 1, E 1 ← (1 - χ)g 1 + yh, E 2 ← yg 1 Zi = Com(zi; ri) = zi (E 1, E 2) + ri (h, g 1) ∑ (Zi ● Ai) = ∑ ((zi(E 1, E 2) + ri(h, g 1)) ● Aᵢ) = (E 1, E 2) ● (∑ zi. Ai) + (h, g 1) ● (∑ ri. Ai) =T =: π

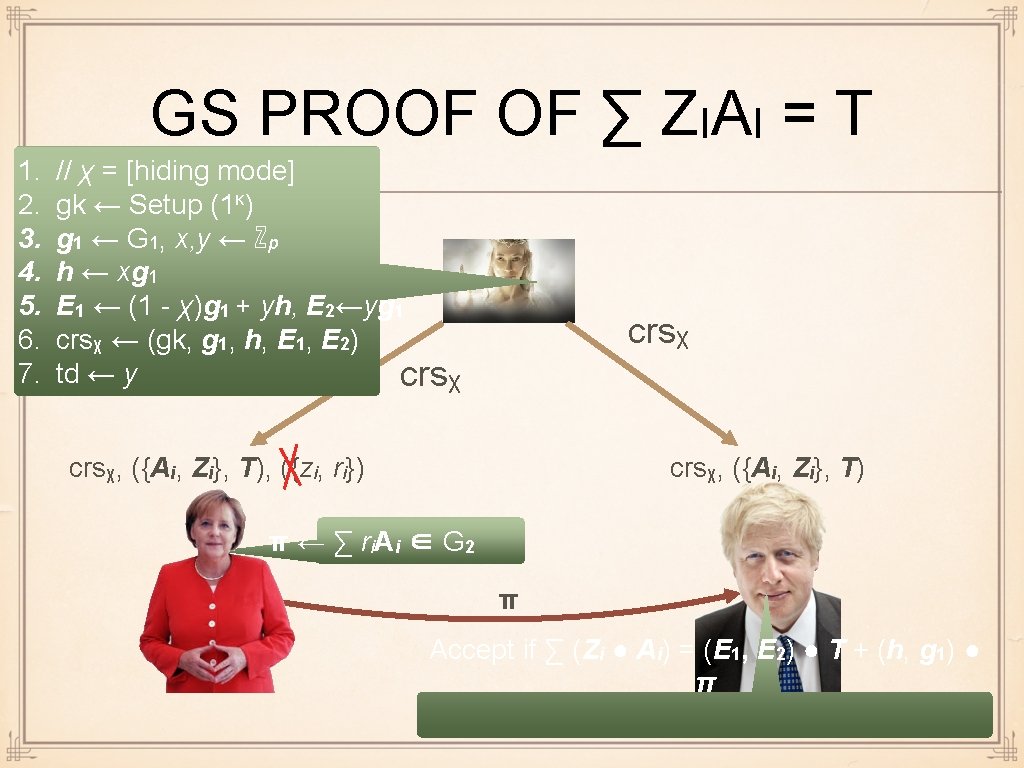
GS PROOF OF ∑ ZIAI = T 1. 2. 3. 4. 5. 6. 7. // χ = [hiding mode] gk ← Setup (1κ) g 1 ← G 1, x, y ← ℤp h ← xg 1 E 1 ← (1 - χ)g 1 + yh, E 2←yg 1 crsχ ← (gk, g 1, h, E 1, E 2) td ← y crsχ, ({Ai, Zi}, T), ({zi, ri}) crsχ, ({Ai, Zi}, T) π ← ∑ ri A i ∈ G 2 π Accept if ∑ (Zi ● Ai) = (E 1, E 2) ● T + (h, g 1) ● π

SOUNDNESS WITH CRS 0 crs 0 = (gk, g 1, h ← xg 1, E 1 ← g 1 + yh, E 2 ← yg 1) Assume Zi = Com(zi; ri) = zi (E₁, E₂) + ri (h, g 1) for some zi Component-wise verification: ∑ (Zi ● Ai) = (E 1, E 2) ● T + (h, g 1) ● π ∑ ê (zi E 1 + ri h, Ai) = ê (E 1, T) + ê (h , π) · x ∑ ê (zi E 2 + ri g 1, Ai) = ê (E 2, T) + ê (g 1, π) ∑ ê ( zi g 1 + 0, Ai) = ê (g 1, T) + 0 Thus ê (g 1, ∑zi Ai) = ê (g 1, T) First - x · second Thus ∑zi Ai = T, as needed

ZERO KNOWLEDGE WITH CRS 1 Consider crs 1 = (gk, g 1, h ← xg 1, E 1 ← yh, E 2 ← yg 1) Trapdoor com. : (E 1, E 2) = y (h, g 1) = Com (0; y) = Com (1; 0) Simulator writes Zi = Com (zi*; ri*) for zi* = 0 and some ri * Basic idea: the simulator creates a GS proof that ∑zi*Ai - t*T = 0, where t* is an opening of (E 1, E 2) Since prover has zi* = zi, t* = 1, the prover must be honest Simulator, knowing y, can take zi* = t* = 0

ZERO KNOWLEDGE Consider crs 1 = (gk, g 1, h ← xg 1, E 1 ← yh, E 2 ← yg 1) (E 1, E 2) = y (h, g 1) = Com (0; y) = Com (1; 0) Simulator writes Zi = Com(0; ri*) = ri* (h, g 1) Simulator creates π* ← ∑ri*Ai - y. T // GS proof for ∑ 0 Ai - 0 T = 0 Verification succeeds: (h, g 1) ● π* = (h, g 1) ● (∑ri*Ai - y. T) = ∑ (ri* (h, g 1) ● Ai) - y (h, g 1) ● T = ∑ (Zi ● Ai) - (E 1, E 2) ● T

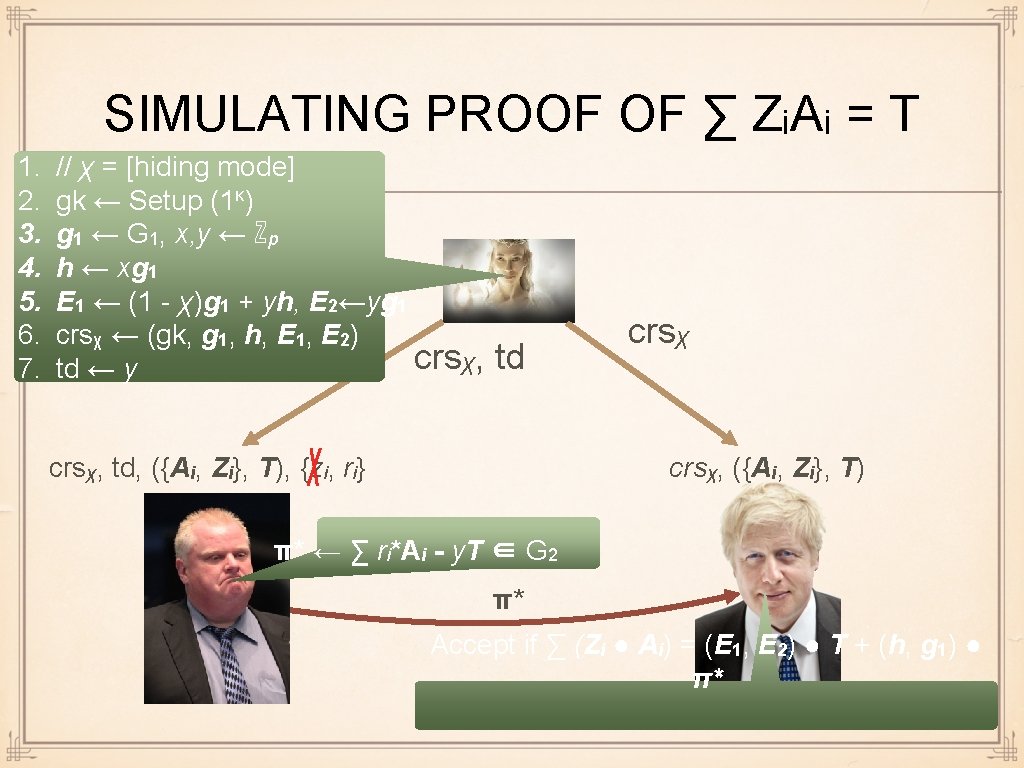
SIMULATING PROOF OF ∑ ZᵢAᵢ = T 1. 2. 3. 4. 5. 6. 7. // χ = [hiding mode] gk ← Setup (1κ) g 1 ← G 1, x, y ← ℤp h ← xg 1 E 1 ← (1 - χ)g 1 + yh, E 2←yg 1 crsχ ← (gk, g 1, h, E 1, E 2) crsχ, td ← y td crsχ, td, ({Ai, Zi}, T), {zi, ri} crsχ, ({Ai, Zi}, T) π* ← ∑ ri*Ai - y. T ∈ G 2 π* Accept if ∑ (Zi ● Ai) = (E 1, E 2) ● T + (h, g 1) ● π*

FIRST GS PROOF DONE We saw how to do one concrete GS proof Details are somewhat scary but the proof is very efficient Prover: n exponentiations Verifier: 2 n + 4 pairings ê We used additive notation, so ag is what was called exponentiation earlier Proof length: 1 group element

SOME OTHER POSSIBLE SETTINGS FOR GS Prove you have committed to Xi, Yi, s. t. ∑ ê (Ai, Yi) + ∑i ∑j aij ê (Xi, Yj) = T or to Xi, yi s. t. ∑ yi Ai + ∑ bj Xj + ∑i∑j yicij. Xj = T where all other values are publicly known

COMPARISON WITH Σ-PROTOCOLS Good: non-interactive, arguably easier to understand (? ) suits well other pairing-based protocols Bad: often less efficient requires specific algebraic structure pairings, while Σ-protocols work in many settings E. g. , Groth-Sahai does not work with Paillier

WHY RELEVANT Pairing-based primitives are "algebraic" Example. Short signature of m with sk x: s = xm In some protocols, cannot reveal signature before the end of the protocol, but you need to prove you know the signature Need GS proof: S = Com (s) ∧pk = xg 1 ∧ s = xm

GS PROOF FOR CIRCUITS Recall that to show that circuit is correctly computed, one only needs a ZK proof that the committed value is Boolean ZK proof that c = Com (mg; r) and m ∈ {0, 1} : Include signatures of 0 and 1 (but nothing else) to the CRS Create a randomized commitment csign of Sign (mg) Construct GS proof that csign commits to a signature of mg

SUBLINEAR NIZK Recent works have made pairing-based NIZK very efficient Drawback: use of very strong non-standard assumptions Knowledge assumption (example): given (g 1, h), it is impossible to compute (yg 1, yh) without knowing y Such assumptions are known to be “non-falsifiable" and many researchers do not like them… but random oracles do not exist --- k. a. -s are better

QAP-BASED SUBLINEAR NIZK [Gennaro, Gentry, . . . , 2013], and follow-up work: computationally sound NIZK to verify correct computation of an arbitrary n-gate arithmetic circuit prover computation: O (n log n) exponentiations proof length: < 10 group elements // independent of n verifier computation: O (|input length|)

STUDY OUTCOMES Efficient NIZK from pairings Basic ideas - product proofs Groth-Sahai proofs

THIS WAS LAST LECTURE This was the last lecture

STUDY OUTCOMES OF THE COURSE Goal of cryptographic protocols: security against malicious adversary security = correctness + privacy General design principles

STUDY OUTCOMES (CONT. ) Most general principle: design passively secure protocol achieve active security by employing ZK proofs

STUDY OUTCOMES: PASSIVE SECURITY Employing homomorphic cryptography Elgamal, Paillier Recursion (BDD, . . . ) Better comp. efficiency by allowing many rounds Glimpse to multi-party computation Glimpse to garbled circuits

STUDY OUTCOMES: ACTIVE SECURITY Σ-protocols Basic protocols, composition Getting full 4 -round ZK from Σ-protocols Pairing-based NIZK protocols Groth-Sahai + some other examples

FURTHER DIRECTIONS Different basic techniques for passive security: lattice-based cryptography, garbled circuits, multi-party computation . . . for active security: cut-and-choose, ZK based on other algebraic techniques Many insanely clever ideas to improve efficiency Other aspects: verification, . . . Concrete applications: e-voting, auctions, e-cash, . . .

THIS COURSE IN FIVE YEARS More emphasis on quantum-safe protocols Lattice-based crypto Fancy applications like fully homomorphic crypto More on information-theoretic crypto // also quantum-safe MPC Need many more hours : )