CRYPTOGRAPHIC PROTOCOLS 2015 LECTURE 6 Trapdoor discrete logarithm

CRYPTOGRAPHIC PROTOCOLS 2015, LECTURE 6 Trapdoor discrete logarithm. Paillier Helger Lipmaa University of Tartu, Estonia

UP TO NOW Introduction to the field Simple secure computation protocols based on DDH ("DL is hard" family) Can design many efficient 2 MAH protocols General problem: Alice needs to compute DL which is hard by assumption Sometimes can ignore by constructing "bitwise" protocols, but still. . .

THIS TIME Trapdoor discrete logarithm hard if you do not know secret key easy if you do Paillier cryptosystem Some protocols E-voting

TRAPDOOR DISCRETE LOGARITHM Def. Binomial coefficient: Relation with exponent. : a = n, b = 1: modulo n²: Idea: while encrypting, use g = 1 + n as a generator in a group modulo n². Needed: can compute DL only while knowing some secret

GETTING CLOSER TO PAILLIER. . . Enc(m; r) = ((n + 1)ᵐ hʳ, (n + 1)ʳ ) mod n² // Analogy to Elgamal possible but not so efficient |Enc (m; r)| = 4 |m| since m∈ ℤn We need later (1 + mn) < n² Paillier cryptosystem (1999): Enc(m; r) = (n + 1)ᵐ rⁿ = (mn + 1) rⁿ mod n² Trapdoor (idea): related to knowledge off factorization of n

SOME ASSUMPTIONS Factoring RSA Strong RSA DCRA Discrete Log CDH DDH Various pairing assumptions SVP RLWE gap. SVP CVP LWE

FACTORING Assumption: given a large composite number, it is infeasible to factor it Not quite: it is easy to factor any even number also say any square numbers Common version: given n = pq, for two random large primes p and q, it is difficult to find p and q

FACTORING Probably the best known hard problem The problem of distinguishing prime numbers from composite numbers and of resolving the latter into their prime factors is known to be one of the most important and useful in arithmetic. ~~~~~~~ Carl Friedrich Gauss Classical computers: subexponential but superpolynomial time (like DL instantiation 1) Quantum computers: easy (like DL)

GETTING CLOSER TO PAILLIER. . . Paillier cryptosystem (1999): for random large p and q, let pk = n ← pq c = Enc(m; r) = (mn + 1) rⁿ mod n² Trapdoor (idea): knowledge of the factoring of n More precisely: trapdoor = i, such that one can recover m efficiently from c� mod n² only if i is known

NOTE ON R Let r = a + bn for a, b < n rⁿ = (a + bn)ⁿ = aⁿ + n · (aⁿ ⁻ ¹bn) +. . . = aⁿ mod n² Thus one can always assume b = 0 Or: r ∈ ℤn*

GETTING CLOSER TO PAILLIER. . . Paillier: c=Enc(m; r) = (mn + 1) rⁿ mod n² Idea: trapdoor = i, such that one can recover m efficiently from c� modn² only if i is known c� mn = ( + 1)� rⁿ� = (1 + imn) rⁿ� modn² Most logical: i is such that rⁿ� = 1 mod n²

RECALL: TOTIENT FUNCTION φ (N) is the order of multiplicative group ℤN* In our case: for any r∈ℤ*n², r^(φ (n²)) = 1 mod n² φ (p) = p - 1 for prime p (0 is not invertible) φ (N) = N · Π (1 - 1 / p') in general product over all distinct primes p' that divide N Here: φ (n²) = p²q² (1 - 1 / p) (1 - 1 / q) = pq(p - 1)(q - 1) = n·φ(n)

FACTORING => Φ Assume knowledge of p, q Can efficiently compute φ : = φ (n) = (p - 1) (q 1)

QUIZ: Φ => FACTORING Assume knowl. of n=pq and φ=(p-1)(q-1)=n(p+q)+1 Knowing n and φ, one can compute s = p + q Knowing n = pq and s : q = s - p, thus n = p (s - p), thus p² - sp + n = 0 Quadratic equation, thus can find p efficiently

GETTING CLOSER TO PAILLIER. . . Paillier: c = Enc(m; r) = (mn + 1) rⁿ mod n² Trapdoor: φ : = (p - 1) (q - 1), μ : = φ⁻¹ mod n Thus (rⁿ)^φ = r^(φ(n²)) = 1 mod n² Thus c^φ = (mn + 1)^φ = φmn + 1 mod n²

GETTING CLOSER TO PAILLIER. . . c^φ = (mn + 1)^φ = φmn + 1 mod n² Decryption: // Need to recover m from c^φ Define L (x) : = (x - 1) / n for x < n² Problem: n is not invertible modulo n² Assuming x < n², this is integer division Thus L(c^φ mod n²) = φ m mod n m ← L(c^φ mod n²) μ mod n (= φ m φ ⁻¹ = m mod n)

PAILLIER ENCRYPTION n public key n φ=(p-1)(q-1), n=pq r∈ℤ n*, m∈ℤn c ← (mn + 1) rⁿ mod n² c* ← c^φ mod n² m ← TDL(c*)μ

PAILLIER ENCRYPTION Paillier. Keygen (gk): p, qn← random keylength-long key n. Paillier. Setup (κ): public 1. primes 1. Choose good keylength (length of p, q) 2. Return gk ← keylength r∈ℤ n*, m∈ℤn 1. 2. 3. φ=(p-1)(q-1), 2. φ ← (p-1)(q-1); μ ← φ⁻ ¹mod n; n ← n=pq pq 3. Return ((φ, μ), n) /* secret key, public key */ c ← (mn + 1) rⁿ mod n² Paillier. Enc (gk, n; m, r): /* Assumes r ← ℤ n*: randomized alg. Paillier. Dec (gk, (φ, μ); c): ← TDL(c^φ mod n²) · μ mod n */ c* 1. ←mc^φ mod n² c ← (mn + 1) rⁿ mod n² 2. Return m m ← TDL(c*)μ Return c

SECURITY If factoring is easy then Paillier can be broken Opposite not known How would you come up with precise security assumption? Tautological assumption. . . : ( but been well known for 15 years

Chosen-Plaintext Attack IND-CPA SECURITY pk n r, e←{0, 1} ( , ₀ m ) ₁ m φ, n c ← (mₑn + 1) rⁿ mod n² e* m ← TDL(c^φ) μ In tautological assumption, m₁ = 0 e* = e ?

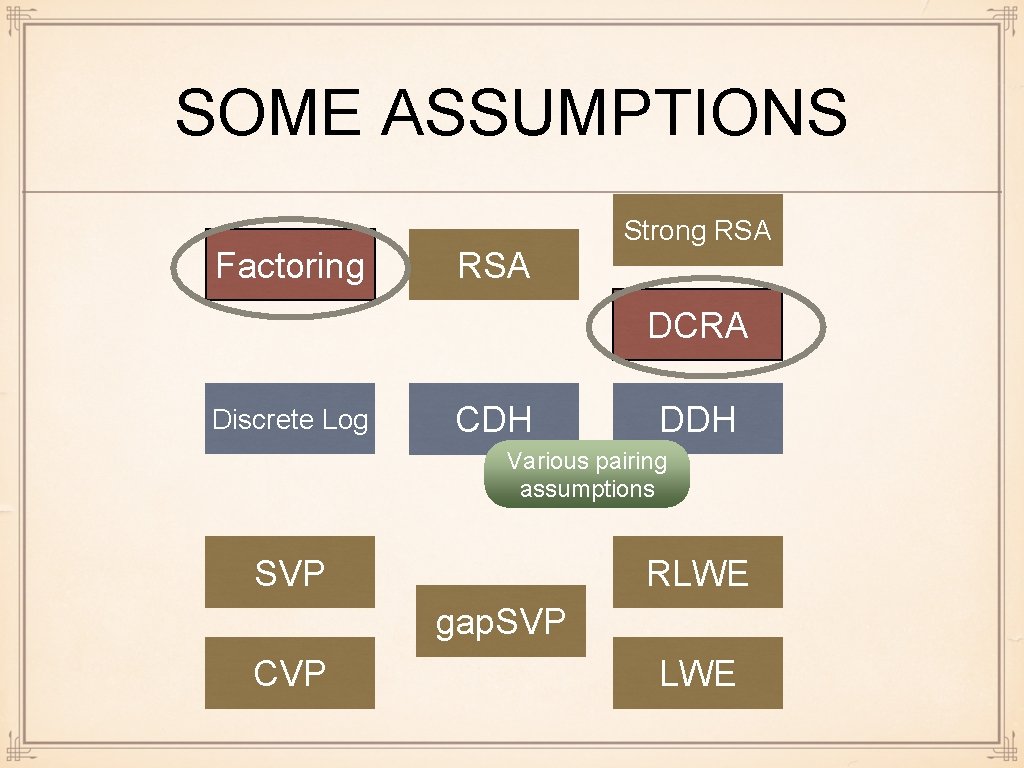
DCR ASSUMPTION Decisional Composite Residuosity Paillier = (Setup, Keygen, Enc, Dec) Adv[DCR] : = | Pr[DCR = 1] - 1 / 2 | Game DCR(κ, A) gk ← Setup (κ) A ε-breaks DCR security iff Adv[DCR] ≥ ((φ, μ), n) ← Keygen (κ) ε m ← ℤn r ← ℤn * DCR is (τ, ε)-secure iff no PPT adversary c₀ ← Enc n; ( m, r) ε-breaks DCRA security in time ≤ τ c₁ ← Enc (n; 0, r) DCR is secure iff it is (poly(κ), negl(κ))- e ← {0, 1} secure e* ← A (n, cₑ) Return e = e* ? 1 : 0

PAILLIER IS IND-CPA SECURE Theorem. DCR is (≈τ, ≈ε)-secure iff Paillier is (τ, ε)IND-CPA secure. Proof idea. DCR states it is difficult to distinguish encryption of 0 from encryption of m. But then it is also difficult to distinguish encryptions of any two plaintexts.

MALLEABILITY OF PAILLIER Recall: Enc (m, r) = (n + 1)ᵐ rⁿ mod n² => Enc (m, r) · Enc (m', r') = Enc (m + m', r · r') Thus, additively homomorphic just remember that randomizer multiplies For example: Enc (m; r) Enc (0; r') = Enc (m; rr')

EFFICIENCY Factoring of n must be hard Thus |n| ≥ 2000 (2|n| = 4000)-bit arithmetic vs 160 -bit arithmetic with Elgamal+elliptic curves Much, much slower. . . but: decryption does not need computation of DL n-bit arithm. on elliptic curves is slower than n-bit modular arithm.

SCALAR PRODUCT PROTOCOL for i = 1 to n rᵢ←ℤn* cᵢ←Enc(aᵢ; rᵢ) pk, sk aᵢ∈{0, 1}ᴸ a={aᵢ: i∈[n]} M←Dec(d) {cᵢ} r'←ℤn* d←Πcᵢ^(bᵢ)·Enc(0; r') Protocol d pk bᵢ∈{0, 1}ᴸ b={bᵢ: i∈[n]} d=Enc(Σaᵢbᵢ; . . . · r') Decryption succeeds when Σaᵢbᵢ ≤ n 2²ᴸ is small, e. g. , n 2²ᴸ M=Σaᵢbᵢ < 2^402^2000

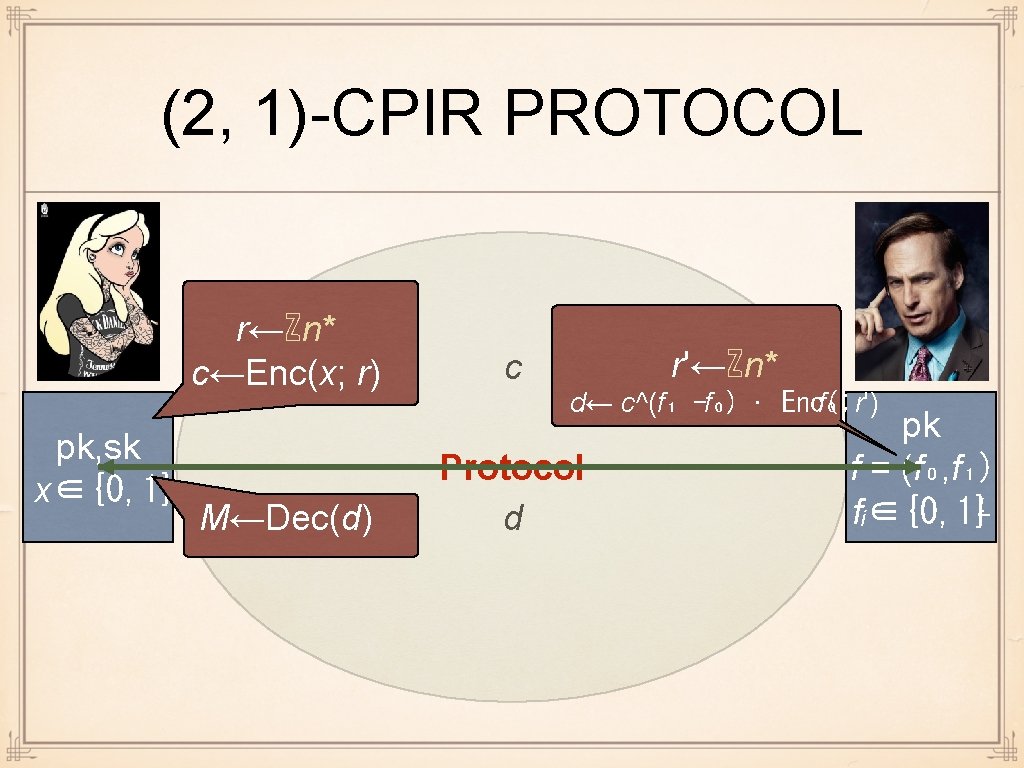
(2, 1)-CPIR PROTOCOL r←ℤn* c←Enc(x; r) pk, sk x∈{0, 1} M←Dec(d) c r'←ℤn* d← c^(f₁ -f₀) · Enc( f₀; r') Protocol d pk f = (f₀, f₁) fᵢ∈{0, 1}ᴸ

CPIR COMPLEXITY Commun. (bits) Alice's comp. (exp, DL) Bob's comp. (exp) 4 · 160 3· 160^(2. 58)+2^(L /2) 5 · 160^(2. 58) Elgamal bitwise (2 L + 2) · 160 (L + 2) · 160^(2. 58) 2 L · 160^(2. 58) Paillier 4000 2 · 4000^(2. 58) Elgamal Concrete keylengths may vary, omitted constants, etc For first protocol, need L ≤ 160 For third protocol, need L ≤ 2000 For larger L, apply protocol many times Need to implement to be able to compare

MORE PROTOCOLS We only saw 2 -message 2 -party protocols but there are many more. . .

E-VOTING: MOTIVATION

E-VOTING: MOTIVATION Motivations: better security direct democracy conveniency

E-VOTING cᵢ cᵢ Tally({cᵢ})

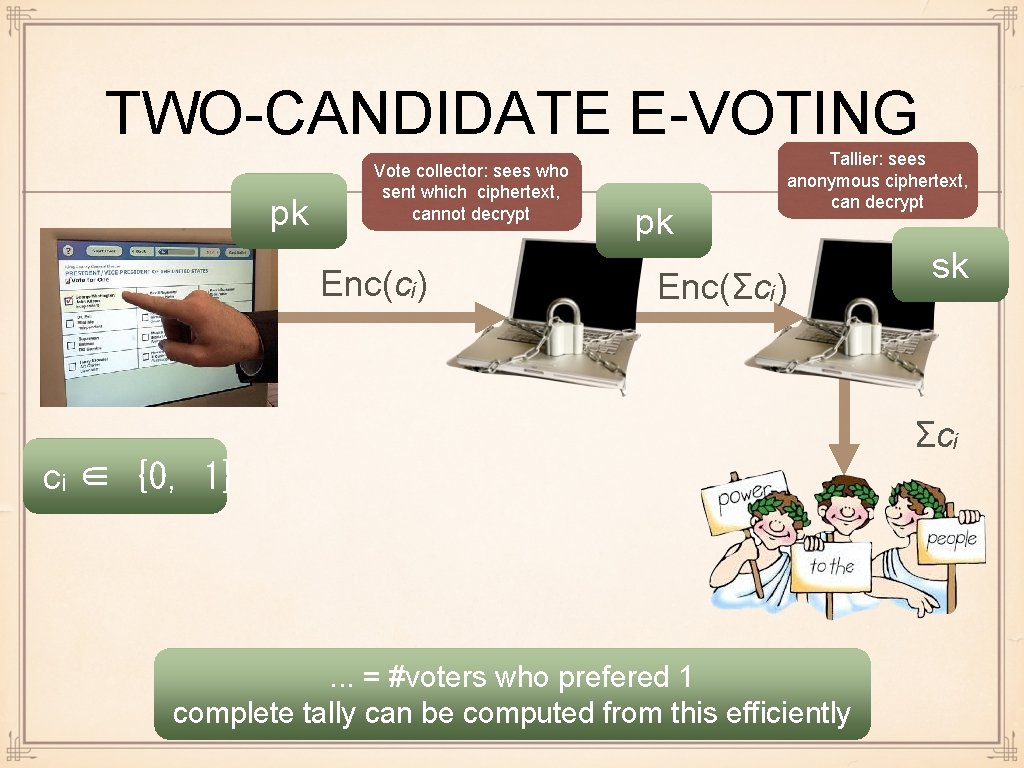
TWO-CANDIDATE E-VOTING pk Vote collector: sees who sent which ciphertext, cannot decrypt Enc(cᵢ) pk Tallier: sees anonymous ciphertext, can decrypt Enc(Σcᵢ) sk Σcᵢ cᵢ ∈ {0, 1} . . . = #voters who prefered 1 complete tally can be computed from this efficiently

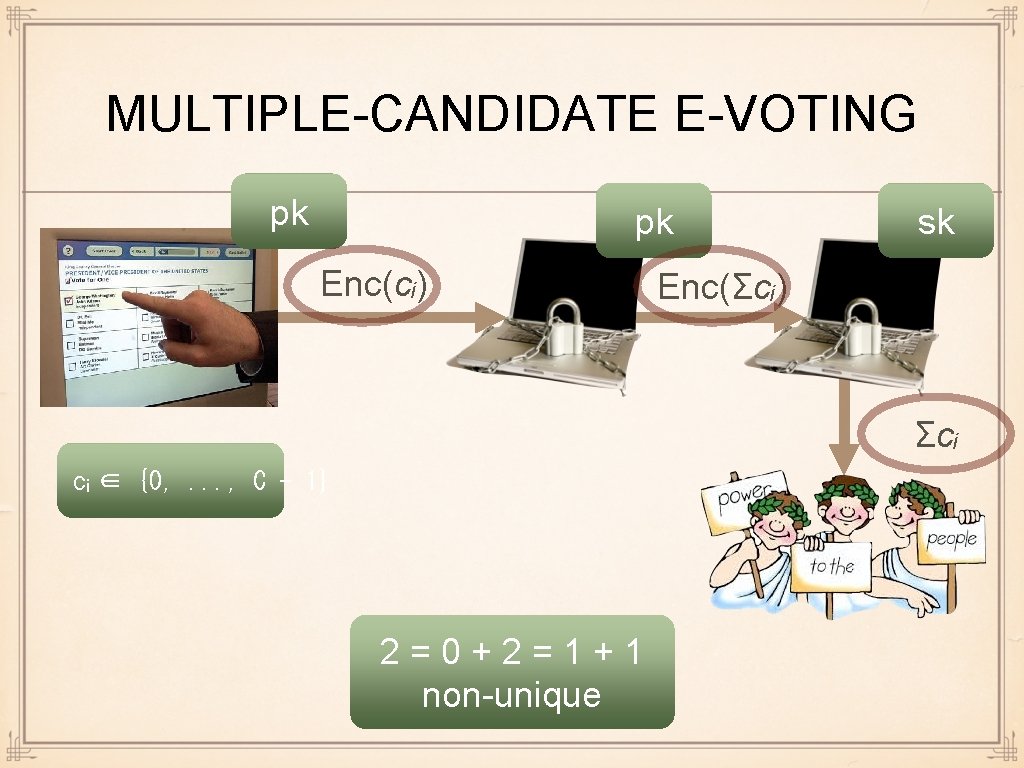
MULTIPLE-CANDIDATE E-VOTING pk pk Enc(cᵢ) sk Enc(Σcᵢ) Σcᵢ cᵢ ∈ {0, . . . , C - 1} 2=0+2=1+1 non-unique

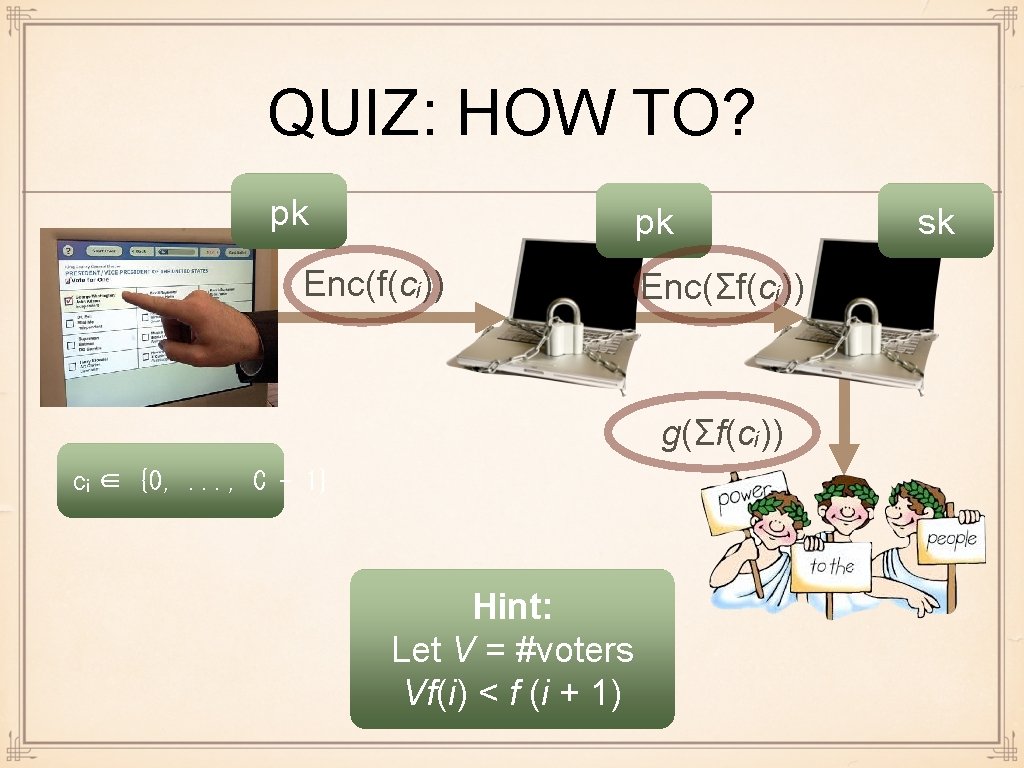
QUIZ: HOW TO? pk pk Enc(f(cᵢ)) Enc(Σf(cᵢ)) g(Σf(cᵢ)) cᵢ ∈ {0, . . . , C - 1} Hint: Let V = #voters Vf(i) < f (i + 1) sk

MULTIPLE VOTERS f (i) : = (V + 1)� Then clearly Vf (i) = V (V + 1)� < (V + 1)� ⁺ ¹ =f (i + 1) presentation in (V+1)ary number system 0 0 1 0 Server 1 outputs Enc (Σᵢ (V + 1)^(cᵢ)) TV . . . T₁ T₀ Voter i outputs Enc ((V + 1)^(cᵢ)) Server 2 outputs Σᵢ (V + 1)^(cᵢ) = Σₑ Tₑ (V + 1)^e

EFFICIENCY The number to be decrypted: ≤ (V + 1)^C Country like Estonia: V = 500 000, C = 150 => (V + 1)^C ≈ 2^(2840) Cannot compute DL of this size! Must use Paillier

NECESSITY OF SECURE COMPUTATION Simpler solution: server 1 just forwards all ciphertexts (in a shuffled order) to server 2 Good: no need for encoding (can use much more complex ballots) server 1 does not need to multiply Bad (efficiency-wise): server 2 must decrypt V ciphertexts Usually server 2 is the bottleneck Decryption much more costly than multiplication

REMARKS: MALICIOUS SECURITY We assumed here that everybody is semihonest-but-curious In real elections, parties can be malicious => All parties must additionally "prove" they acted In the alternative solution of correctly Second part of the lecture series the previous slide, the first server must prove shuffling was done correctly "mixnet" However, one must first design a protocol secure in semihonest model

STUDY OUTCOMES Trapdoor discrete logarithm: idea Paillier with all gory details Example: efficiency of Paillier E-voting

WHAT NEXT? We saw how to use homomorphism to obtain interesting protocols However, the number of such protocols is limited Next lectures: adding tools: recursion, multiple rounds