Contemporary Logic Design Arithmetic Circuits Part II Randy

Contemporary Logic Design Arithmetic Circuits (Part II) Randy H. Katz University of California, Berkeley Spring 2007 © R. H. Katz Lecture #24: Arithmetic Circuits -1

Contemporary Logic Design Arithmetic Circuits Overview • BCD Circuits • Combinational Multiplier Circuit • Design Case Study: 8 Bit Multiplier • Sequential Multiplier Circuit © R. H. Katz Lecture #24: Arithmetic Circuits -2

Contemporary Logic Design Arithmetic Circuits BCD Addition BCD Number Representation Decimal digits 0 thru 9 represented as 0000 thru 1001 in binary Addition: 5 = 0101 3 = 0011 8 = 1000 = 8 1101 = 13! Problem when digit sum exceeds 9 Solution: add 6 (0110) if sum exceeds 9! 5 = 0101 9 = 1001 8 = 1000 7 = 0111 1101 6 = 0110 1 0011 = 1 3 in BCD 1 0000 = 16 in binary 6 = 0110 1 0110 = 1 6 in BCD © R. H. Katz Lecture #24: Arithmetic Circuits -3

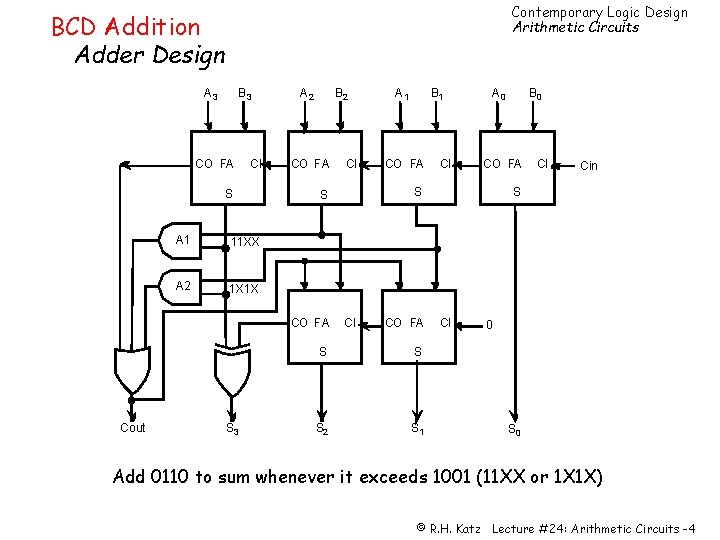
Contemporary Logic Design Arithmetic Circuits BCD Addition Adder Design A 3 B 3 CO FA CI S A 1 11 XX A 2 1 X 1 X A 2 B 2 CO FA S 3 B 1 CO FA CI A 0 CI CO FA S S S 2 S 1 B 0 CO FA S S CO FA Cout CI A 1 CI Cin S CI 0 S 0 Add 0110 to sum whenever it exceeds 1001 (11 XX or 1 X 1 X) © R. H. Katz Lecture #24: Arithmetic Circuits -4

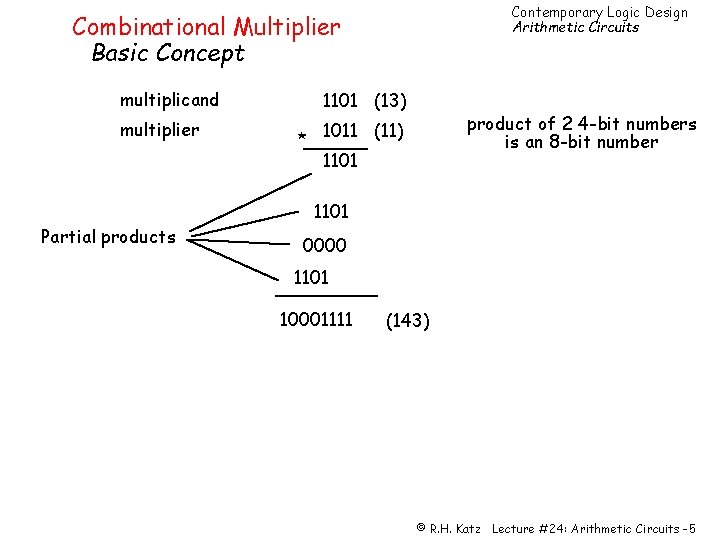
Contemporary Logic Design Arithmetic Circuits Combinational Multiplier Basic Concept multiplicand multiplier Partial products 1101 (13) product of 2 4 -bit numbers is an 8 -bit number * 1011 (11) 1101 0000 1101 10001111 (143) © R. H. Katz Lecture #24: Arithmetic Circuits -5

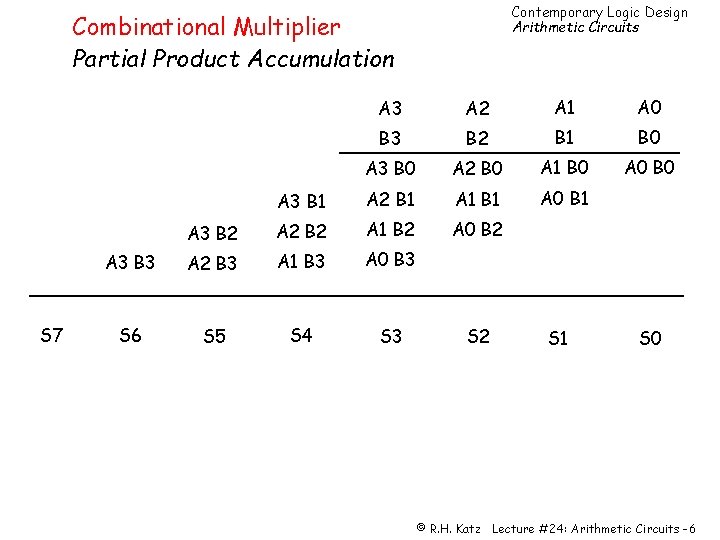
Contemporary Logic Design Arithmetic Circuits Combinational Multiplier Partial Product Accumulation S 7 A 3 A 2 A 1 A 0 B 3 B 2 B 1 B 0 A 3 B 0 A 2 B 0 A 1 B 0 A 0 B 0 A 3 B 1 A 2 B 1 A 1 B 1 A 0 B 1 A 3 B 2 A 2 B 2 A 1 B 2 A 0 B 2 A 3 B 3 A 2 B 3 A 1 B 3 A 0 B 3 S 6 S 5 S 4 S 3 S 2 S 1 S 0 © R. H. Katz Lecture #24: Arithmetic Circuits -6

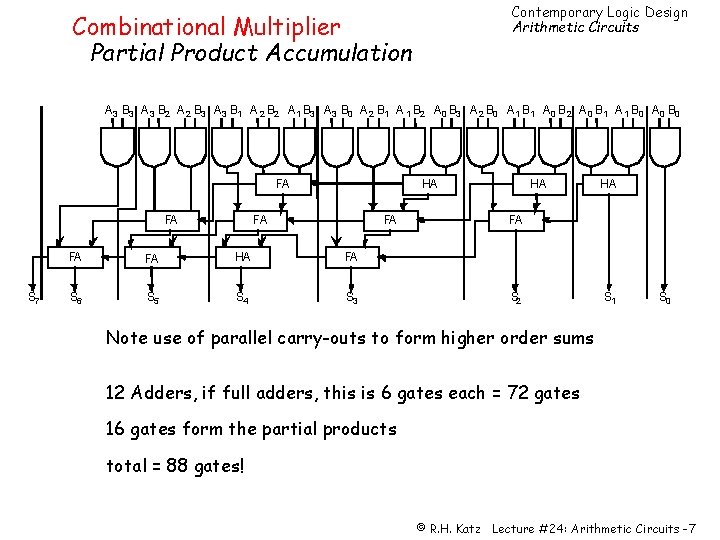
Contemporary Logic Design Arithmetic Circuits Combinational Multiplier Partial Product Accumulation A 3 B 3 A 3 B 2 A 2 B 3 A 3 B 1 A 2 B 2 A 1 B 3 A 3 B 0 A 2 B 1 A 1 B 2 A 0 B 3 A 2 B 0 A 1 B 1 A 0 B 2 A 0 B 1 A 1 B 0 A 0 B 0 FA FA S 7 HA FA FA HA FA S 6 S 5 S 4 S 3 HA HA FA S 2 S 1 S 0 Note use of parallel carry-outs to form higher order sums 12 Adders, if full adders, this is 6 gates each = 72 gates 16 gates form the partial products total = 88 gates! © R. H. Katz Lecture #24: Arithmetic Circuits -7

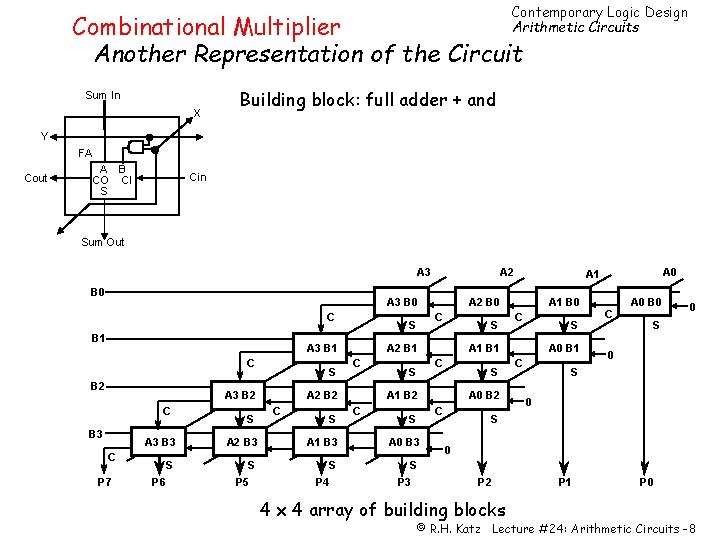
Contemporary Logic Design Arithmetic Circuits Combinational Multiplier Another Representation of the Circuit Sum In X Building block: full adder + and Y FA Cout A B CO CI S Cin Sum Out A 3 B 0 A 2 A 3 B 0 C B 1 S A 3 B 1 C B 2 S A 3 B 2 C B 3 C S S S A 1 B 3 A 0 B 3 S S P 5 P 4 P 3 A 0 B 2 C A 2 B 3 P 6 S A 1 B 2 C A 1 B 0 C S A 1 B 1 C A 3 B 3 C P 7 S S A 2 B 1 A 2 B 2 C A 2 B 0 C A 0 A 1 A 0 B 1 C A 0 B 0 C 0 S 0 S 0 P 2 4 x 4 array of building blocks P 1 P 0 © R. H. Katz Lecture #24: Arithmetic Circuits -8

Contemporary Logic Design Arithmetic Circuits Case Study: 8 x 8 Multiplier Problem Decomposition How to implement 8 x 8 multiply in terms of 4 x 4 multiplies? A 7 -4 A 3 -0 * B 7 -4 B 3 -0 A 3 -0 * B 3 -0 8 bit products A 7 -4 * B 3 -0 = PP 1 A 3 -0 * B 7 -4 = PP 2 A 7 -4 * B 7 -4 P 15 -12 = PP 0 P 11 -8 = PP 3 P 7 -4 P 3 -0 = PP 0 3 -0 P 7 -4 = PP 0 + PP 1 + PP 2 + Carry-in 3 -0 3 -0 P 11 -8 = PP 1 + PP 2 + PP 3 + Carry-in 7 -4 3 -0 P 15 -12 = PP 3 + Carry-in 7 -4 © R. H. Katz Lecture #24: Arithmetic Circuits -10

Case Study: 8 x 8 Multiplier Calculation of Partial Products Contemporary Logic Design Arithmetic Circuits Use 4 4 x 4 multipliers to create the 4 partial products © R. H. Katz Lecture #24: Arithmetic Circuits -11

Contemporary Logic Design Arithmetic Circuits Case Study: 8 x 8 Multiplier Three-At-A-Time Adder Clever use of the Carry Inputs Sum A[3 -0], B[3 -0], C[3 -0]: Two Level Full Adder Circuit Note: Carry lookahead schemes also possible! © R. H. Katz Lecture #24: Arithmetic Circuits -12

Contemporary Logic Design Arithmetic Circuits Case Study: 8 x 8 Multiplier Three-At-A-Time Adder with TTL Components Full Adder 4 -bit ALU/Adder Full Adders (2 per package) Standard ALU configured as 4 -bit cascaded adder (with internal carry lookahead) Note the off-set in the outputs © R. H. Katz Lecture #24: Arithmetic Circuits -13

Case Study: 8 x 8 Multiplier Accumulation of Partial Products FA 4 -bit ALU/Adder FA FA FA 4 -bit ALU/Adder Contemporary Logic Design Arithmetic Circuits FA FA 4 -bit ALU/Adder Just a case of cascaded three-at-a-time adders! © R. H. Katz Lecture #24: Arithmetic Circuits -14

Contemporary Logic Design Arithmetic Circuits Case Study: 8 x 8 Multiplier The Complete System (Actual TTL packages) © R. H. Katz Lecture #24: Arithmetic Circuits -15

Case Study: 8 x 8 Multiplier Package Count and Performance Contemporary Logic Design Arithmetic Circuits 4 74284/74285 pairs = 8 packages 4 74183, 3 74181, 1 74182 = 8 packages 16 packages total Partial product calculation (74284/285) = 40 ns typ, 60 ns max Intermediate sums (74183) = 9 ns/20 ns = 15 ns average, 33 ns max Second stage sums w/carry lookahead 74 LS 181: carry G and P = 20 ns typ, 30 ns max 74182: second level carries = 13 ns typ, 22 ns max 74 LS 181: formations of sums = 15 ns typ, 26 ns max 103 ns typ, 171 ns max © R. H. Katz Lecture #24: Arithmetic Circuits -16

Contemporary Logic Design Arithmetic Circuits Sequential Multiplier • 4 -Bit Multiplier Example: 3 x 4 = 12 – Four cycles to completion Cycle Multiplier Multiplicand Product Initialize 0011 0000 0100 0000 Cycle 0, Multiplier[0]=1 0000 1000 0100 Cycle 1, Multiplier[0]=1 0000 1100 Cycle 2, Multiplier[0]=0 0000 0010 0000 1100 Cycle 3, Multiplier[0]=0 0000 0100 0000 1100 Product = 0 For i = 0 to 3 do If Multiplier[0] = 1 then Product = Product + Multiplicand Shift right the Multiplier Shift left the Multiplicand © R. H. Katz Lecture #24: Arithmetic Circuits -17

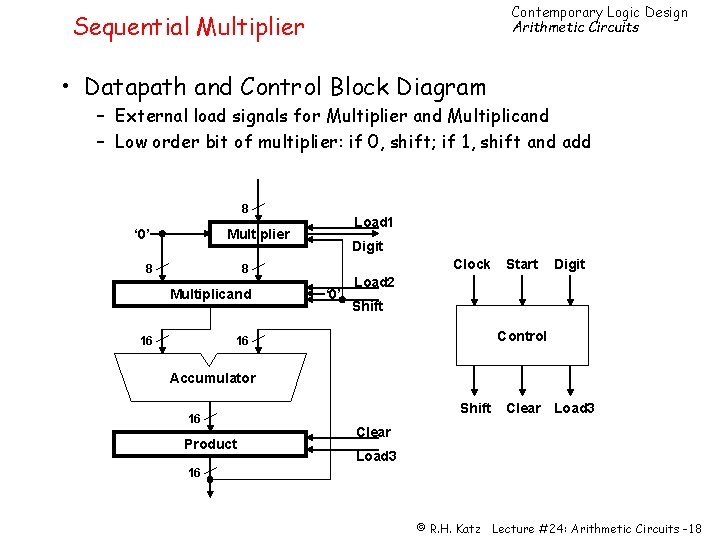
Contemporary Logic Design Arithmetic Circuits Sequential Multiplier • Datapath and Control Block Diagram – External load signals for Multiplier and Multiplicand – Low order bit of multiplier: if 0, shift; if 1, shift and add 8 Load 1 Multiplier ‘ 0’ 8 Digit Clock 8 Multiplicand 16 ‘ 0’ Start Digit Load 2 Shift Control 16 Accumulator 16 Product Shift Clear Load 3 16 © R. H. Katz Lecture #24: Arithmetic Circuits -18

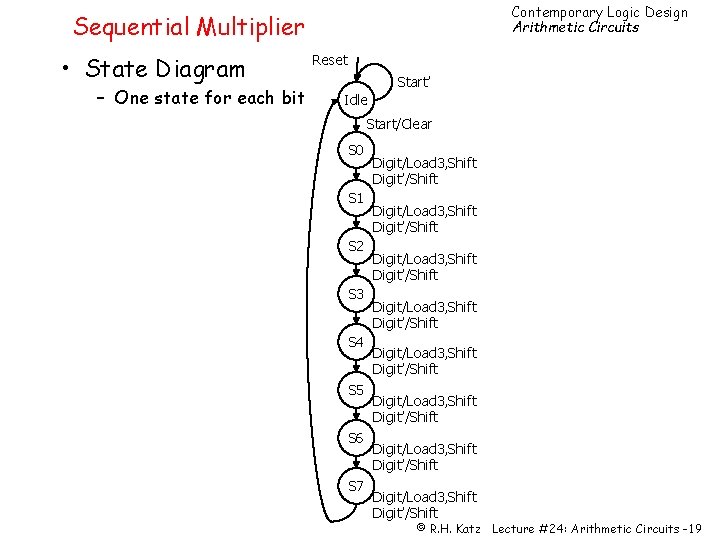
Contemporary Logic Design Arithmetic Circuits Sequential Multiplier • State Diagram – One state for each bit Reset Start’ Idle Start/Clear S 0 S 1 S 2 S 3 S 4 S 5 S 6 S 7 Digit/Load 3, Shift Digit’/Shift Digit/Load 3, Shift Digit’/Shift © R. H. Katz Lecture #24: Arithmetic Circuits -19

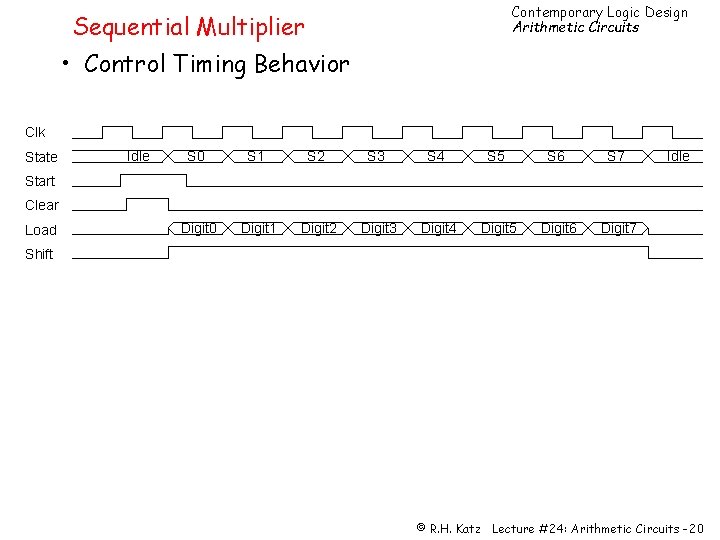
Contemporary Logic Design Arithmetic Circuits Sequential Multiplier • Control Timing Behavior Clk State Idle S 0 S 1 S 2 S 3 S 4 S 5 S 6 S 7 Digit 0 Digit 1 Digit 2 Digit 3 Digit 4 Digit 5 Digit 6 Digit 7 Idle Start Clear Load Shift © R. H. Katz Lecture #24: Arithmetic Circuits -20

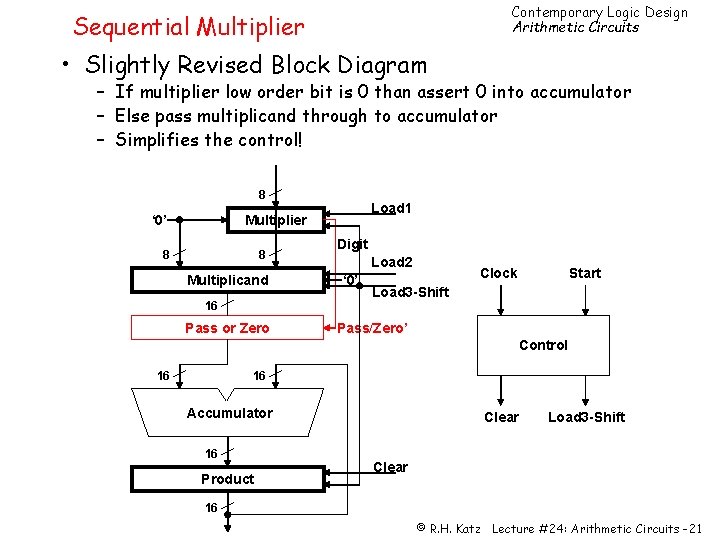
Contemporary Logic Design Arithmetic Circuits Sequential Multiplier • Slightly Revised Block Diagram – If multiplier low order bit is 0 than assert 0 into accumulator – Else pass multiplicand through to accumulator – Simplifies the control! 8 Load 1 Multiplier ‘ 0’ 8 8 Multiplicand 16 Pass or Zero Digit Load 2 ‘ 0’ Clock Start Load 3 -Shift Pass/Zero’ Control 16 16 Accumulator 16 Product Clear Load 3 -Shift Clear 16 © R. H. Katz Lecture #24: Arithmetic Circuits -21

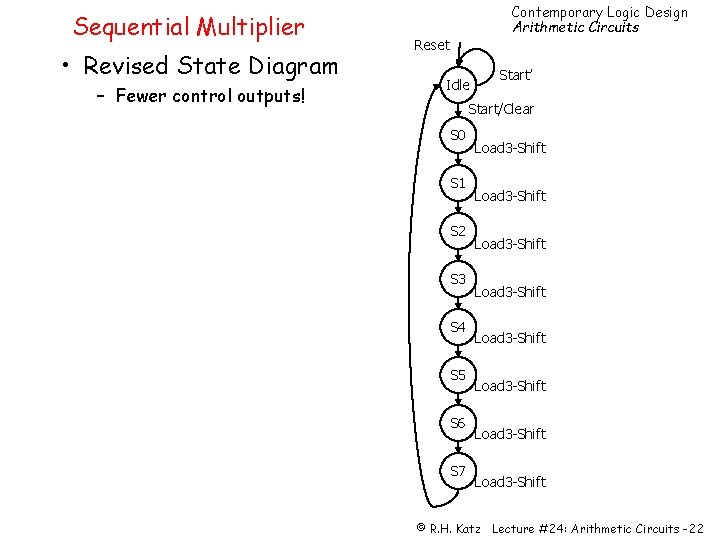
Sequential Multiplier • Revised State Diagram – Fewer control outputs! Contemporary Logic Design Arithmetic Circuits Reset Idle Start’ Start/Clear S 0 S 1 S 2 S 3 S 4 S 5 S 6 S 7 Load 3 -Shift Load 3 -Shift © R. H. Katz Lecture #24: Arithmetic Circuits -22

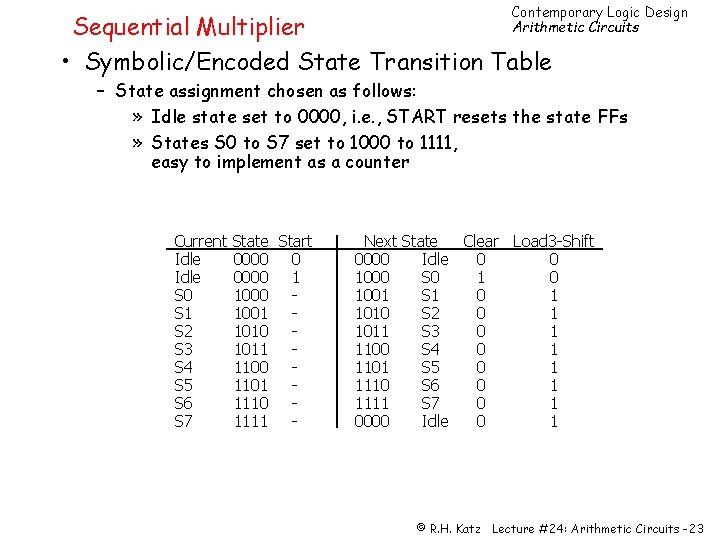
Contemporary Logic Design Arithmetic Circuits Sequential Multiplier • Symbolic/Encoded State Transition Table – State assignment chosen as follows: » Idle state set to 0000, i. e. , START resets the state FFs » States S 0 to S 7 set to 1000 to 1111, easy to implement as a counter Current Idle S 0 S 1 S 2 S 3 S 4 S 5 S 6 S 7 State Start 0000 0 0000 1 1000 1001 1010 1011 1100 1101 1110 1111 - Next State Clear Load 3 -Shift 0000 Idle 0 0 1000 S 0 1001 S 1 0 1 1010 S 2 0 1 1011 S 3 0 1 1100 S 4 0 1 1101 S 5 0 1 1110 S 6 0 1 1111 S 7 0 1 0000 Idle 0 1 © R. H. Katz Lecture #24: Arithmetic Circuits -23

Booth Multiplier Contemporary Logic Design Arithmetic Circuits Searching for ways to speed up the basic multiply step • Tricky encoding scheme to reduce the number of stages in a binary multiplier • Considers two bits at a time rather than one—this cuts the number of multiplier steps in half • Each step is slightly more complex compared to the simple multiplier, but is almost as fast as the basic multiplier stage that it replaces © R. H. Katz Lecture #24: Arithmetic Circuits -24

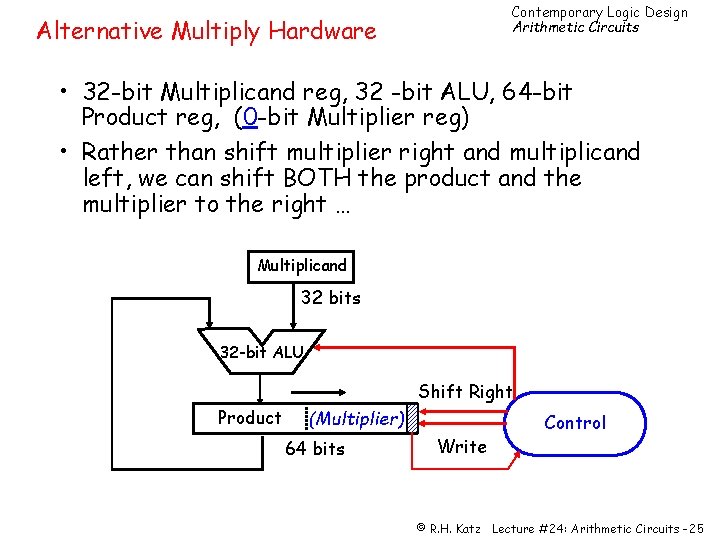
Contemporary Logic Design Arithmetic Circuits Alternative Multiply Hardware • 32 -bit Multiplicand reg, 32 -bit ALU, 64 -bit Product reg, (0 -bit Multiplier reg) • Rather than shift multiplier right and multiplicand left, we can shift BOTH the product and the multiplier to the right … Multiplicand 32 bits 32 -bit ALU Shift Right Product (Multiplier) 64 bits Write Control © R. H. Katz Lecture #24: Arithmetic Circuits -25

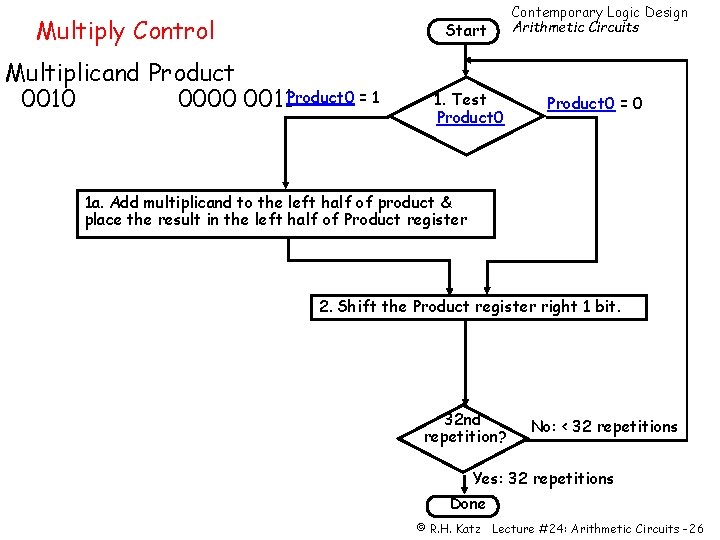
Multiply Control Start Multiplicand Product 0010 0000 0011 Product 0 = 1 1. Test Product 0 Contemporary Logic Design Arithmetic Circuits Product 0 = 0 1 a. Add multiplicand to the left half of product & place the result in the left half of Product register 2. Shift the Product register right 1 bit. 32 nd repetition? No: < 32 repetitions Yes: 32 repetitions Done © R. H. Katz Lecture #24: Arithmetic Circuits -26

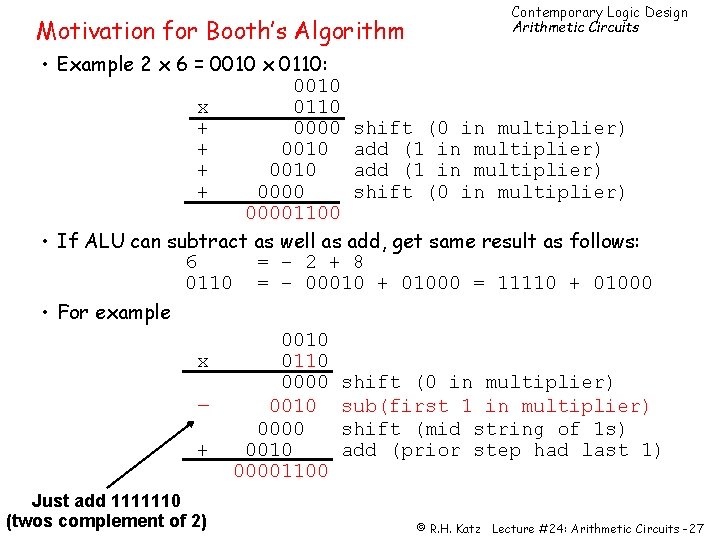
Motivation for Booth’s Algorithm Contemporary Logic Design Arithmetic Circuits • Example 2 x 6 = 0010 x 0110: 0010 x 0110 + 0000 shift (0 in multiplier) + 0010 add (1 in multiplier) + 0000 shift (0 in multiplier) 00001100 • If ALU can subtract as well as add, get same result as follows: 6 = – 2 + 8 0110 = – 00010 + 01000 = 11110 + 01000 • For example 0010 x 0110 0000 shift (0 in multiplier) – 0010 sub(first 1 in multiplier) 0000 shift (mid string of 1 s) + 0010 add (prior step had last 1) 00001100 Just add 1111110 (twos complement of 2) © R. H. Katz Lecture #24: Arithmetic Circuits -27

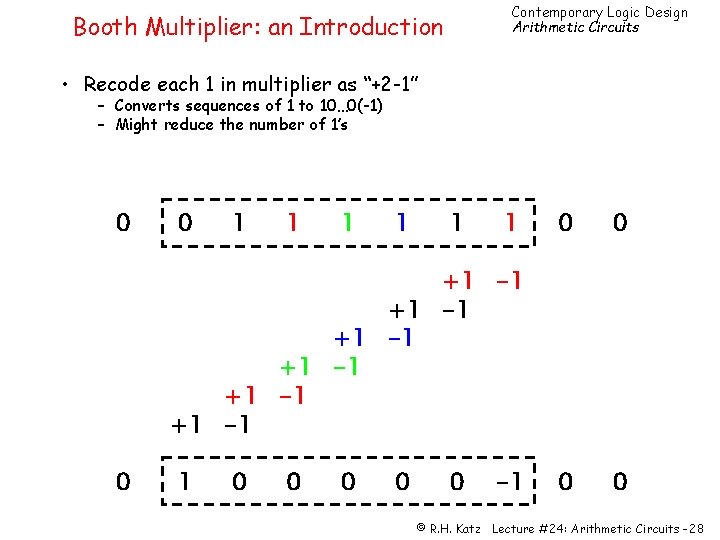
Contemporary Logic Design Arithmetic Circuits Booth Multiplier: an Introduction • Recode each 1 in multiplier as “+2 -1” – Converts sequences of 1 to 10… 0(-1) – Might reduce the number of 1’s 0 0 1 1 1 0 0 +1 -1 +1 -1 0 1 0 0 0 -1 © R. H. Katz Lecture #24: Arithmetic Circuits -28

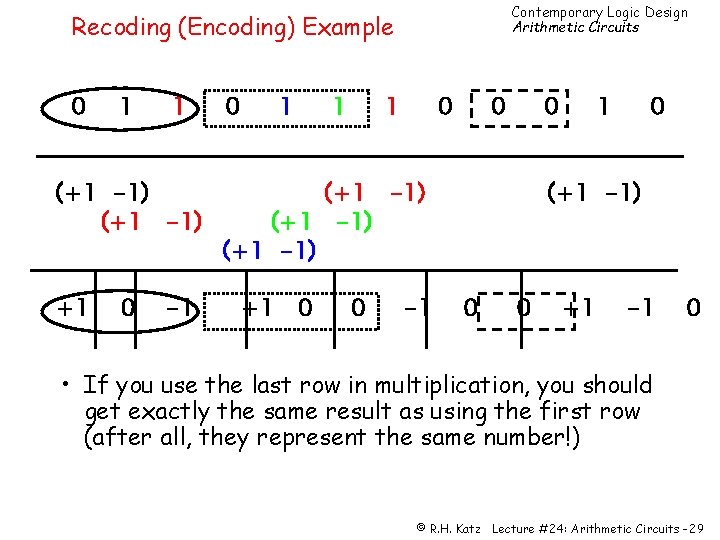
Contemporary Logic Design Arithmetic Circuits Recoding (Encoding) Example 0 1 1 (+1 -1) +1 0 -1 0 1 1 1 0 0 0 (+1 -1) +1 0 0 -1 1 0 (+1 -1) 0 0 +1 -1 0 • If you use the last row in multiplication, you should get exactly the same result as using the first row (after all, they represent the same number!) © R. H. Katz Lecture #24: Arithmetic Circuits -29

Contemporary Logic Design Arithmetic Circuits Booth Multiplication Example 0 0 1 1 1 Sign extension +1 0 0 01 1 1 0 0 0 0 0 1 1 0 0 6 x 0 14 0 -1 0 0 0 (-6) 0 0 0 1 0 0 84 © R. H. Katz Lecture #24: Arithmetic Circuits -30

Contemporary Logic Design Arithmetic Circuits Booth’s Algorithm: Implementation Approach end of run middle of run beginning of run 011110 Current Bit to the Right Explanation Example. Op 1 0 Begins run of 1 s 0001111000 sub 1 1 Middle of run of 1 s 0001111000 none 0 1 End of run of 1 s 0001111000 add 0 0 Middle of run of 0 s 0001111000 none Originally for Speed (when shift is faster than add, it is advantageous to replace adds and subs with shifts) Basic idea: replace a string of 1 s in multiplier with an initial subtract for rightmost 1 in a run of 1’s, then later add back a 1 for the bit to the left of the last 1 in the run – 1 + 10000 01111 © R. H. Katz Lecture #24: Arithmetic Circuits -31

Contemporary Logic Design Arithmetic Circuits Booth’s Example (2 x 7) Operation Multiplicand Product next? 0. initial value 0010 0000 0111 0 10 -> sub 1 a. P = P - m 1110 0111 0 + 1110 shift P (sign ext) 1 b. 0010 1111 0011 1 11 -> nop, shift 2. 0010 1111 1001 1 11 -> nop, shift 3. 0010 1111 1100 1 01 -> add 4 a. 0010 0001 1100 1 4 b. 0010 + 0010 shift 0000 1110 0 done © R. H. Katz Lecture #24: Arithmetic Circuits -32

Contemporary Logic Design Arithmetic Circuits Booth’s Example (2 x -3) Operation Multiplicand 0. initial value 0010 1 a. P = P - m 1110 1101 0 Product next? 0000 1101 0 +1110 shift P (sign ext) 1 b. 0010 + 0010 1111 0110 1 01 -> add 2 a. 0001 0110 1 shift P 2 b. + 0010 1110 0000 1011 0 10 -> sub 3 a. 0010 1110 1011 0 shift 3 b. 0010 4 a 4 b. 0010 1111 0101 1 shift 1111 1010 1 done 10 -> sub 11 -> nop © R. H. Katz Lecture #24: Arithmetic Circuits -33

Lecture Review Contemporary Logic Design Arithmetic Circuits We have covered: • BCD Adders Simple extension of binary adders • Multipliers 4 x 4 multiplier: partial product accumulation extension to 8 x 8 case • Sequential Multipliers • Booth Multiply Step Recoding to speed up the calculation © R. H. Katz Lecture #24: Arithmetic Circuits -34