cole des Hautes tudes Industrielles Dpartement Automatique Cours

École des Hautes Études Industrielles - Département Automatique Cours d’automatique H. E. I. 3 tronc commun

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Introduction Présentation, (groupe provisoire) Ce cours de 22 h. (11 séances) s’intéresse aux systèmes logiques (numériques) et se divise en trois parties : § Logique combinatoire (4 h. ), § Logique séquentielle (5 à 6 h. ), § Grafcet (12 à 13 h. ). Chacune de ces parties est accompagnée d’une séance de T. D. de 2 h. (6 h. de T. D. ). § T. D. en fin de poly, § Préparation exigée,

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Introduction 4 séances de T. P. de 4 h. (16 h. T. P. ) après cours et T. D. (1 compte rendu à la fin de chaque T. P. ) : § Logique combinatoire, § Logique séquentielle, § Automate, § Grafcet. 1 D. S. de 3 h. après le cours

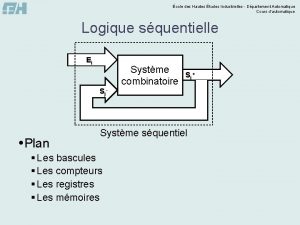
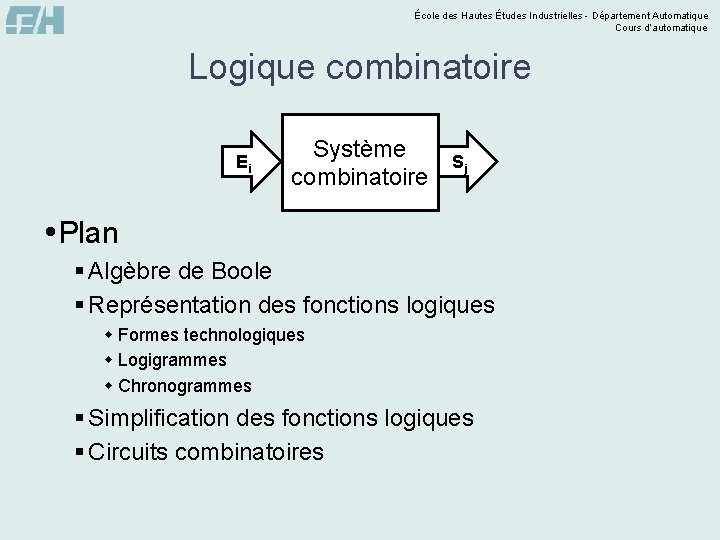
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Logique combinatoire Ei Système combinatoire Sj Plan § Algèbre de Boole § Représentation des fonctions logiques w Formes technologiques w Logigrammes w Chronogrammes § Simplification des fonctions logiques § Circuits combinatoires

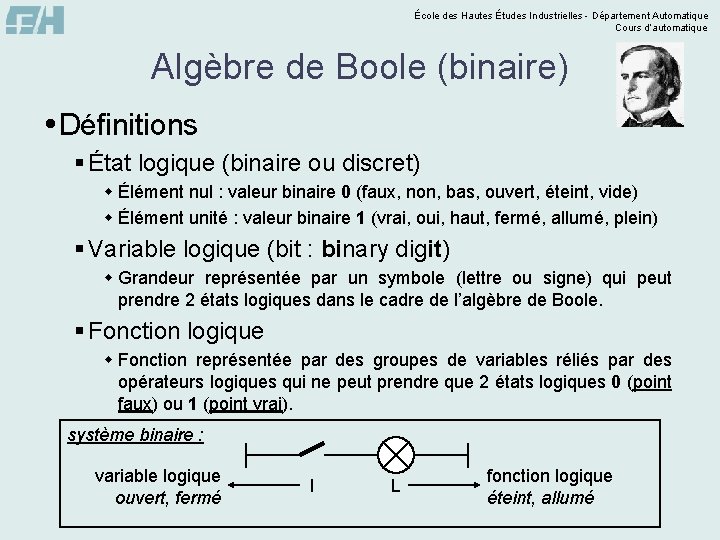
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole (binaire) Définitions § État logique (binaire ou discret) w Élément nul : valeur binaire 0 (faux, non, bas, ouvert, éteint, vide) w Élément unité : valeur binaire 1 (vrai, oui, haut, fermé, allumé, plein) § Variable logique (bit : binary digit) w Grandeur représentée par un symbole (lettre ou signe) qui peut prendre 2 états logiques dans le cadre de l’algèbre de Boole. § Fonction logique w Fonction représentée par des groupes de variables réliés par des opérateurs logiques qui ne peut prendre que 2 états logiques 0 (point faux) ou 1 (point vrai). système binaire : variable logique ouvert, fermé I L fonction logique éteint, allumé

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole Représentation des variables et fonctions logiques § Algébrique (forme littérale) : w Équation, proposition, expression w Formes technologiques w Formes canoniques § Graphique : w Table de vérité w Tableau de Karnaugh w Diagramme d’Euler ou de Venn (théorie des ensembles) § Temporelle : w Chronogramme § Symbolique : w Logigramme § Numérique (écriture condensée)

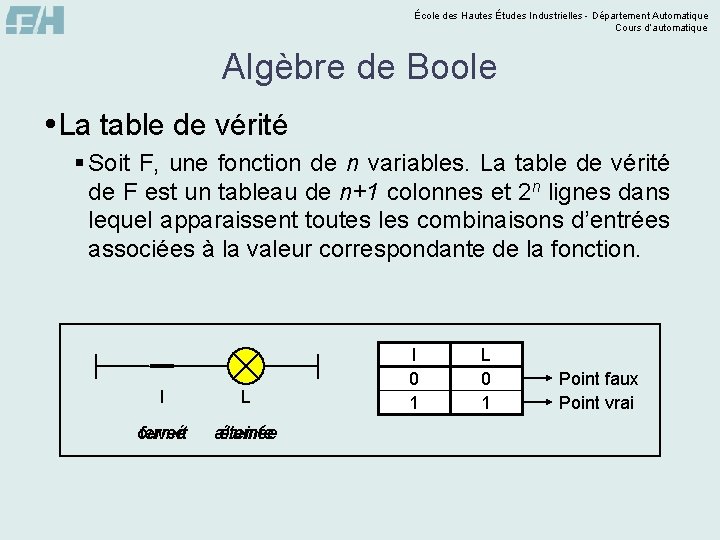
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole La table de vérité § Soit F, une fonction de n variables. La table de vérité de F est un tableau de n+1 colonnes et 2 n lignes dans lequel apparaissent toutes les combinaisons d’entrées associées à la valeur correspondante de la fonction. I L ouvert fermé allumée éteinte I 0 1 L 0 1 Point faux Point vrai

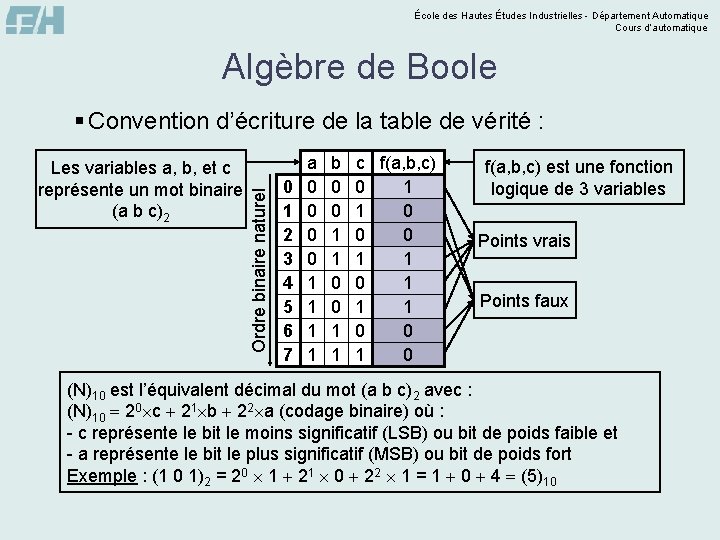
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole Les variables a, b, et c représente un mot binaire (a b c)2 Ordre binaire naturel § Convention d’écriture de la table de vérité : 0 1 2 3 4 5 6 7 a 0 0 1 1 b 0 0 1 1 c f(a, b, c) 1 0 0 1 1 1 0 0 1 0 f(a, b, c) est une fonction logique de 3 variables Points vrais Points faux (N)10 est l’équivalent décimal du mot (a b c)2 avec : (N)10 20´c 21´b 22´a (codage binaire) où : - c représente le bit le moins significatif (LSB) ou bit de poids faible et - a représente le bit le plus significatif (MSB) ou bit de poids fort Exemple : (1 0 1)2 = 20 ´ 1 21 ´ 0 22 ´ 1 = 1 0 4 (5)10

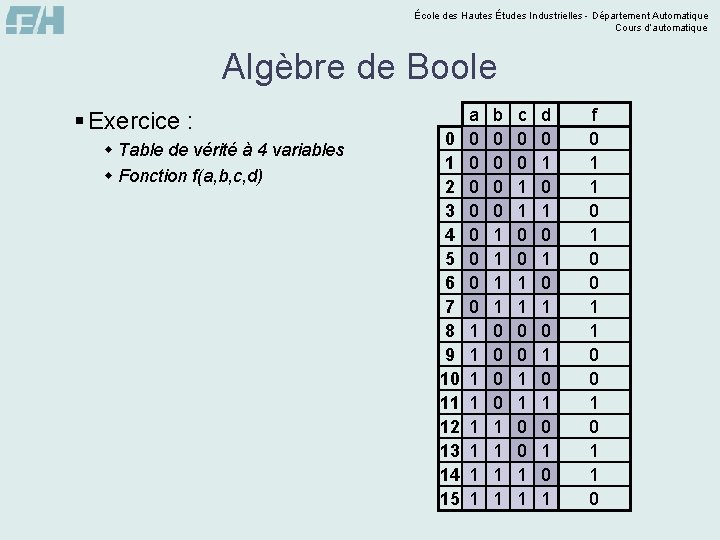
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § Exercice : w Table de vérité à 4 variables w Fonction f(a, b, c, d) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 a 0 0 0 0 1 1 1 1 b 0 0 0 0 1 1 1 1 c 0 0 1 1 d 0 1 0 1 f 0 1 1 0 0 1 1 0

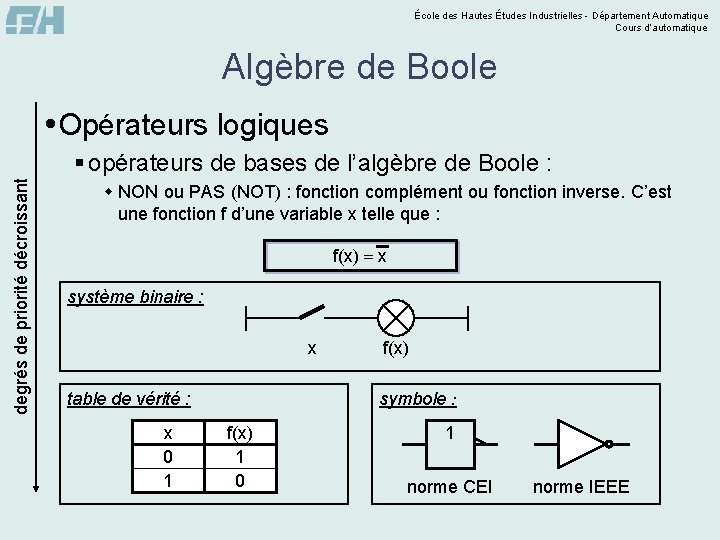
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole Opérateurs logiques degrés de priorité décroissant § opérateurs de bases de l’algèbre de Boole : w NON ou PAS (NOT) : fonction complément ou fonction inverse. C’est une fonction f d’une variable x telle que : f(x) x système binaire : x symbole : table de vérité : x 0 1 f(x) 1 0 1 norme CEI norme IEEE

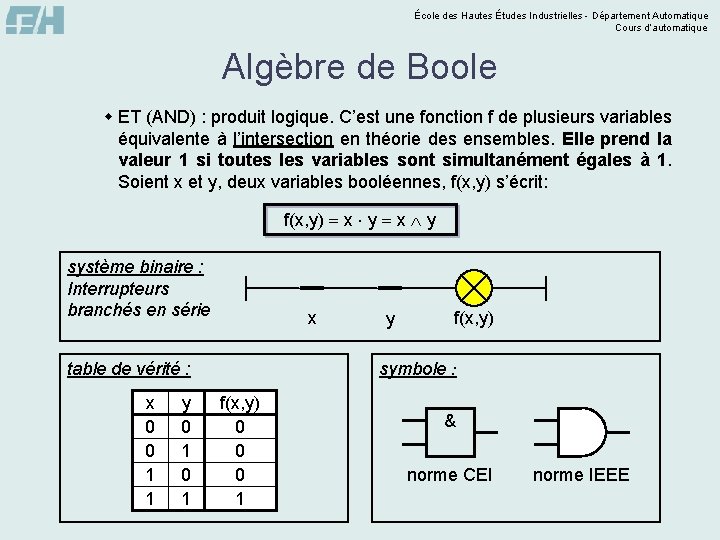
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole w ET (AND) : produit logique. C’est une fonction f de plusieurs variables équivalente à l’intersection en théorie des ensembles. Elle prend la valeur 1 si toutes les variables sont simultanément égales à 1. Soient x et y, deux variables booléennes, f(x, y) s’écrit: f(x, y) x y système binaire : Interrupteurs branchés en série x y 0 1 f(x, y) symbole : table de vérité : x 0 0 1 1 y f(x, y) 0 0 0 1 & norme CEI norme IEEE

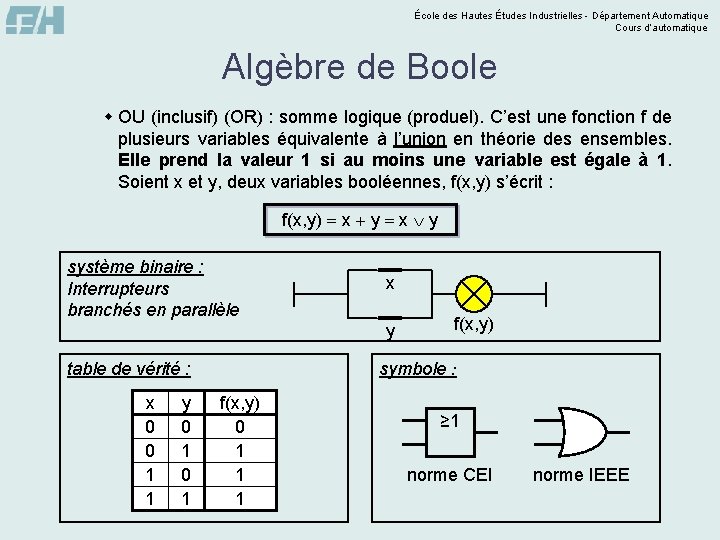
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole w OU (inclusif) (OR) : somme logique (produel). C’est une fonction f de plusieurs variables équivalente à l’union en théorie des ensembles. Elle prend la valeur 1 si au moins une variable est égale à 1. Soient x et y, deux variables booléennes, f(x, y) s’écrit : f(x, y) x y système binaire : Interrupteurs branchés en parallèle x y symbole : table de vérité : x 0 0 1 1 y 0 1 f(x, y) 0 1 1 1 ≥ 1 norme CEI norme IEEE

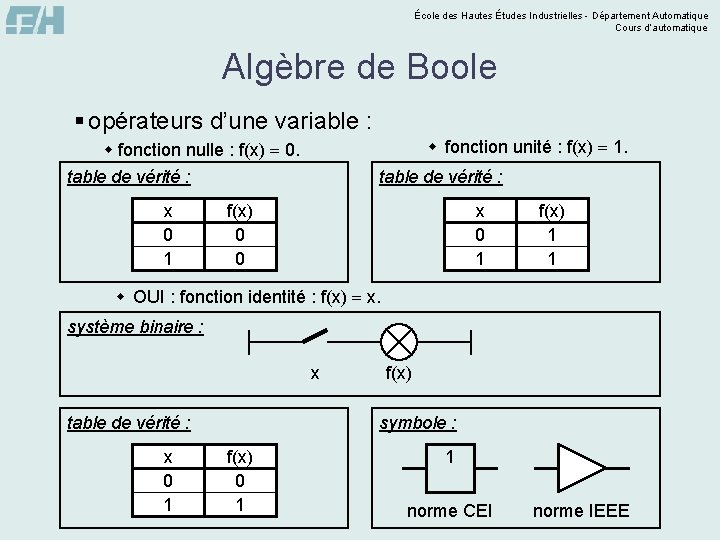
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § opérateurs d’une variable : w fonction unité : f(x) 1. w fonction nulle : f(x) 0. table de vérité : x 0 1 table de vérité : f(x) 0 0 x 0 1 f(x) 1 1 w OUI : fonction identité : f(x) x. système binaire : x table de vérité : x 0 1 f(x) symbole : f(x) 0 1 1 norme CEI norme IEEE

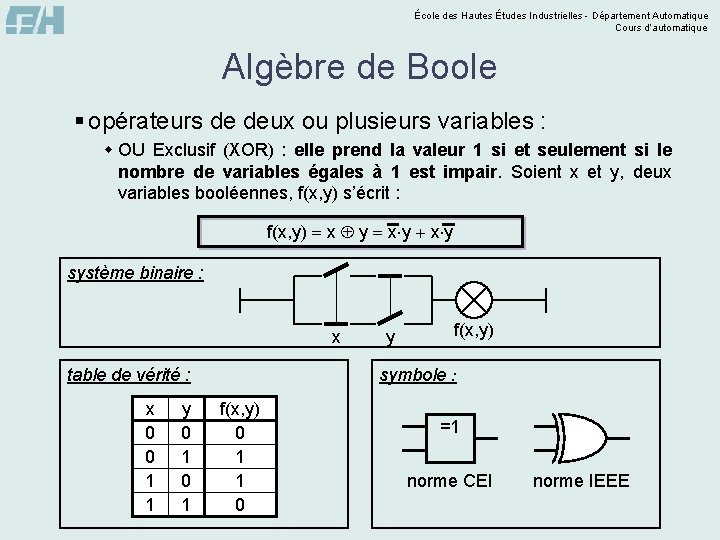
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § opérateurs de deux ou plusieurs variables : w OU Exclusif (XOR) : elle prend la valeur 1 si et seulement si le nombre de variables égales à 1 est impair. Soient x et y, deux variables booléennes, f(x, y) s’écrit : f(x, y) x y x y système binaire : x y 0 1 f(x, y) symbole : table de vérité : x 0 0 1 1 y f(x, y) 0 1 1 0 =1 norme CEI norme IEEE

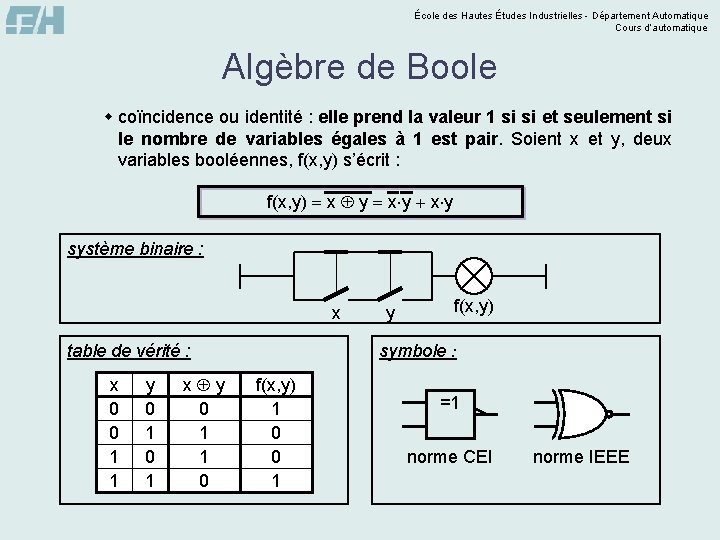
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole w coïncidence ou identité : elle prend la valeur 1 si si et seulement si le nombre de variables égales à 1 est pair. Soient x et y, deux variables booléennes, f(x, y) s’écrit : f(x, y) x y x y système binaire : x y 0 1 1 0 f(x, y) symbole : table de vérité : x 0 0 1 1 y f(x, y) 1 0 0 1 =1 norme CEI norme IEEE

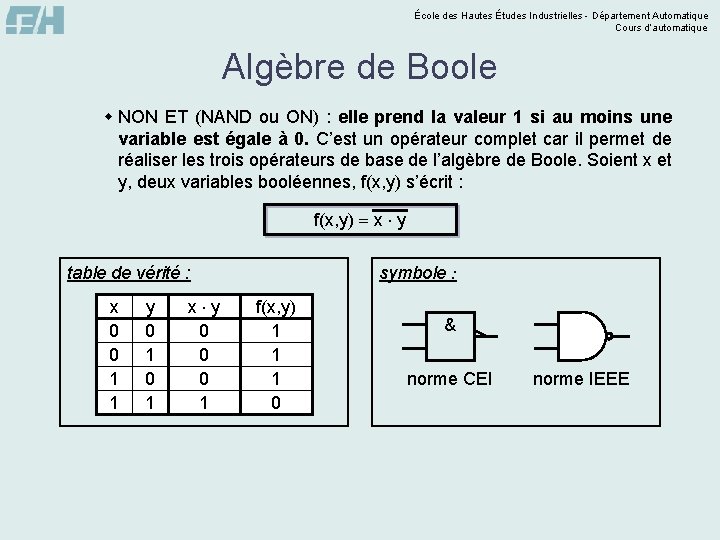
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole w NON ET (NAND ou ON) : elle prend la valeur 1 si au moins une variable est égale à 0. C’est un opérateur complet car il permet de réaliser les trois opérateurs de base de l’algèbre de Boole. Soient x et y, deux variables booléennes, f(x, y) s’écrit : f(x, y) x y symbole : table de vérité : x 0 0 1 1 y 0 1 x y 0 0 0 1 f(x, y) 1 1 1 0 & norme CEI norme IEEE

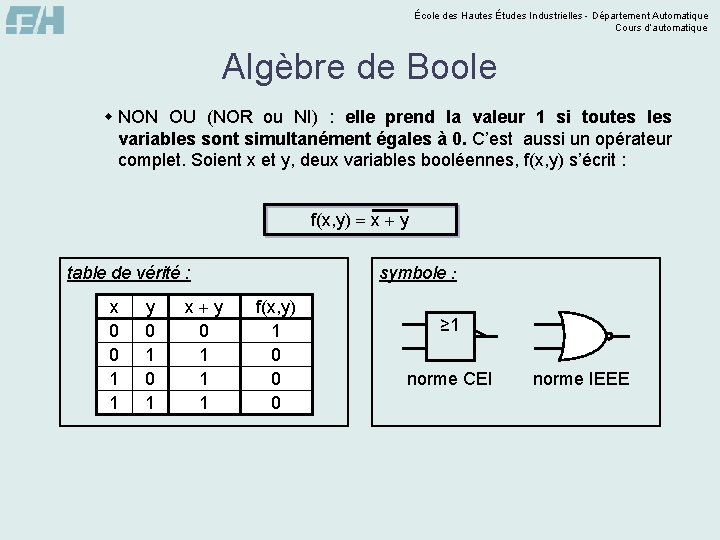
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole w NON OU (NOR ou NI) : elle prend la valeur 1 si toutes les variables sont simultanément égales à 0. C’est aussi un opérateur complet. Soient x et y, deux variables booléennes, f(x, y) s’écrit : f(x, y) x y symbole : table de vérité : x 0 0 1 1 y 0 1 x y 0 1 1 1 f(x, y) 1 0 0 0 ≥ 1 norme CEI norme IEEE

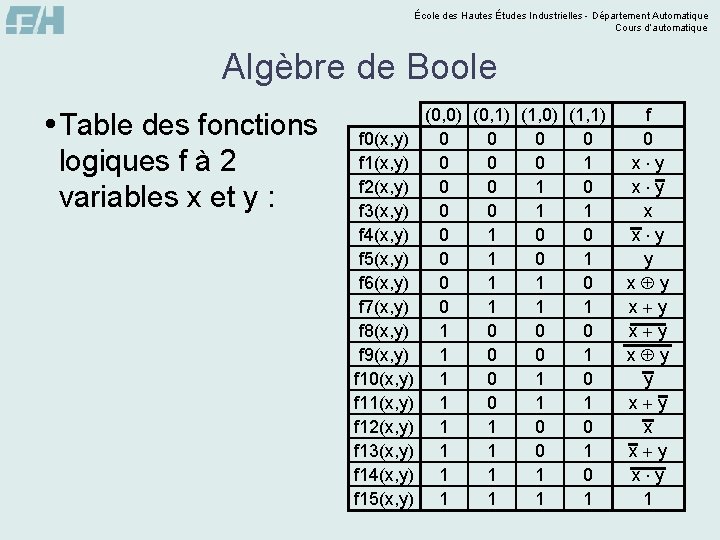
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole Table des fonctions logiques f à 2 variables x et y : f 0(x, y) f 1(x, y) f 2(x, y) f 3(x, y) f 4(x, y) f 5(x, y) f 6(x, y) f 7(x, y) f 8(x, y) f 9(x, y) f 10(x, y) f 11(x, y) f 12(x, y) f 13(x, y) f 14(x, y) f 15(x, y) (0, 0) (0, 1) (1, 0) (1, 1) 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 f 0 x y x x y y x y x y y x x y 1

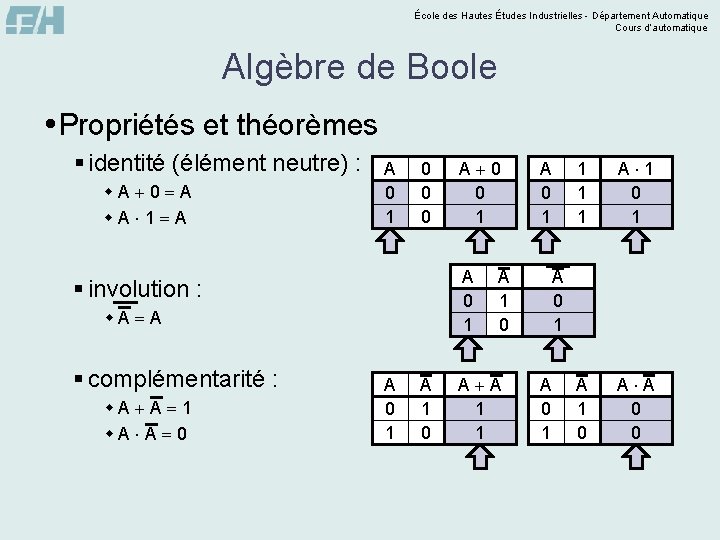
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole Propriétés et théorèmes § identité (élément neutre) : w. A 0 A w. A 1 A A 0 1 0 0 0 A 0 1 § involution : w. A A § complémentarité : w. A A 1 w. A A 0 0 1 A 1 0 A A 1 1 1 A 1 0 A A 0 0 A 0 1

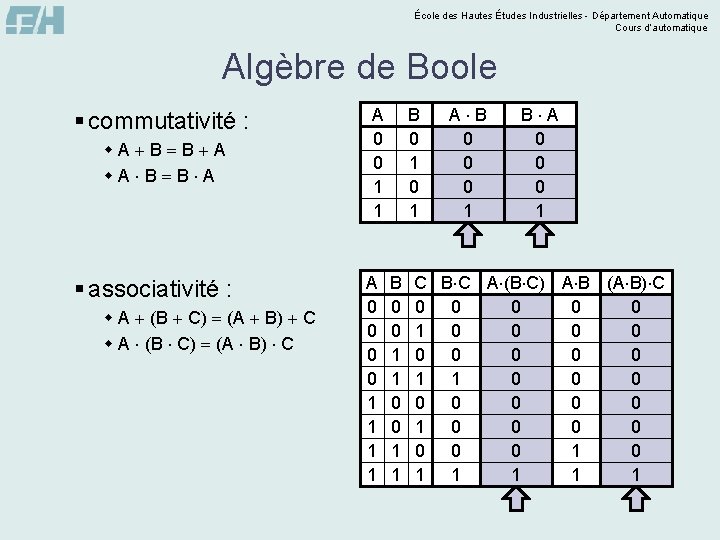
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § commutativité : w. A B B A § associativité : w A (B C) (A B) C A 0 0 1 1 B 0 1 B 0 0 1 1 A A B B 0 1 0 1 B B A A 0 1 0 1 C B C A (B C) A B (A B) C 0 0 0 1 1 1 0 0 0 1 0 1 1 1 1 0 0 0 0 1 0 1 1 1 0 0 1 0 1 1 1

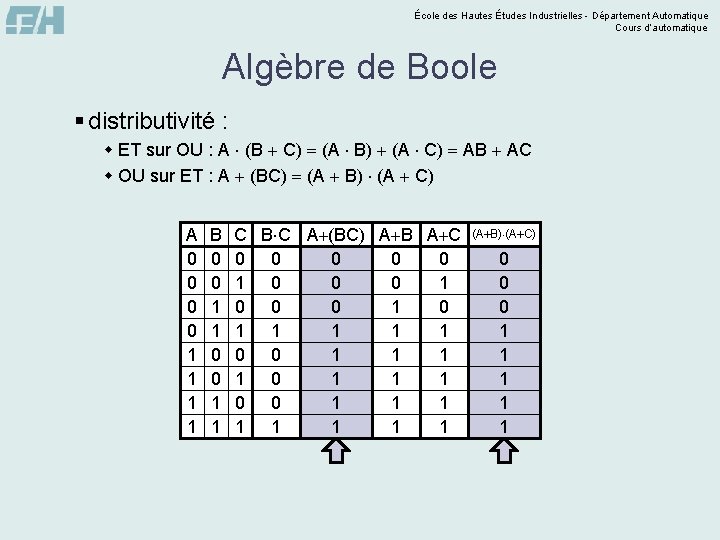
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § distributivité : w ET sur OU : A (B C) (A B) (A C) AB AC w OU sur ET : A (BC) (A B) (A C) A 0 0 1 1 B 0 0 1 1 C B C A (B C) A (BC) A B A C (A B) (A C) AB AC 0 0 0 1 0 0 1 0 0 0 1 1 1 1 1 0 0 1 1 1

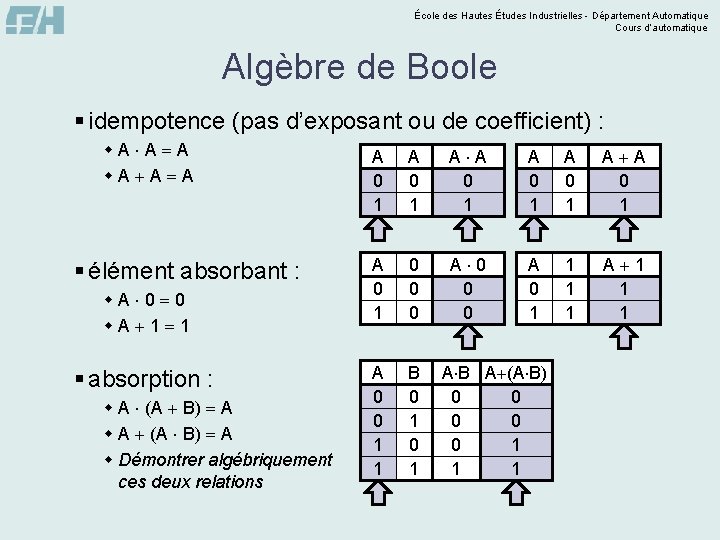
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § idempotence (pas d’exposant ou de coefficient) : w. A A A § élément absorbant : w. A 0 0 w. A 1 1 § absorption : w A (A B) A w Démontrer algébriquement ces deux relations A 0 1 A A 0 1 0 0 0 A 0 1 1 A 1 1 1 A 0 0 1 1 B 0 1 A B A (A B) 0 0 1 0 0 0 1 1

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § De Morgan : w. A B A B A 0 0 1 1 B 0 1 A B 0 1 0 1 A B 1 1 0 0 1 0 A 1 1 0 0 B 1 0 A B 1 0 1 1 0 0 § autre identité à démontrer algébriquement : w AB B w (A B) B w A AB A B w A (A B) AB § principe de dualité w L’expression duale de toute expression logique (pas équation) s’obtient en permutant les opérateurs ET et OU et les éléments 0 et 1 apparaissant dans l’expression.

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Algèbre de Boole § Exercice : w En utilisant les définitions, propriétés et théorèmes de l’algèbre de Boole développer et simplifier la fonction définie par l’équation suivante : F(a, b, c, d, e) a b b c ce de

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques Les formes technologiques § première forme : somme de monômes (produits de littéraux). C’est une forme disjonctive. Exemple : F(x, y, z) xy xz xy § deuxième forme : produit de monaux (somme de littéraux). C’est une forme conjonctive. Exemple : F(x, y, z) (x y) (x z)(x y) § formes technologiques associées : elles s’obtiennent d’après le théorème d’involution et celui de De Morgan.

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques Les formes normales ou canoniques § une fonction logique est sous forme canonique si chaque termes (monômes et monaux) contient toutes les variables. C’est aussi une forme technologique. § forme normale disjonctive (1ère forme canonique) : somme de monômes contenant chacun toutes les variables (intersection de base ou min terme). Exemple : F(x, y, z) x y z § forme normale conjonctive (2ème forme canonique) : produit de monaux contenant chacun toutes les variables (réunion de base ou max terme). Exemple : F(x, y, z) (x y z)(x y z)

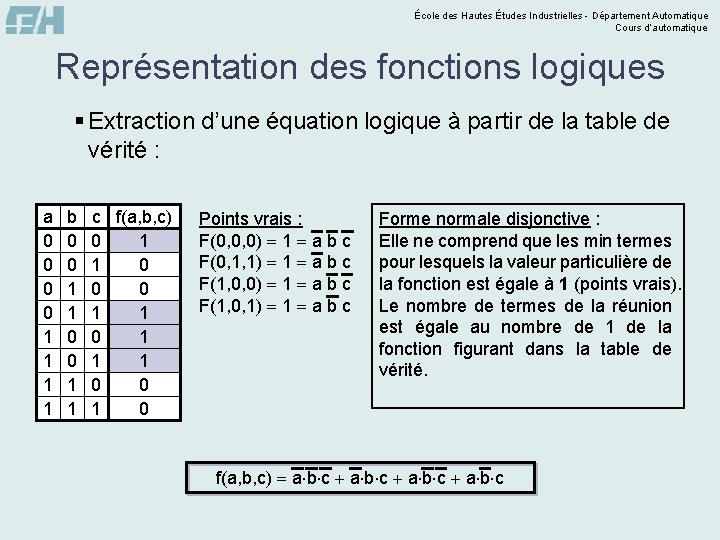
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Extraction d’une équation logique à partir de la table de vérité : a 0 0 1 1 b 0 0 1 1 c f(a, b, c) 1 0 0 0 1 1 1 0 0 1 0 Points vrais : F(0, 0, 0) 1 a b c F(0, 1, 1) 1 a b c F(1, 0, 0) 1 a b c F(1, 0, 1) 1 a b c Forme normale disjonctive : Elle ne comprend que les min termes pour lesquels la valeur particulière de la fonction est égale à 1 (points vrais). Le nombre de termes de la réunion est égale au nombre de 1 de la fonction figurant dans la table de vérité. f(a, b, c) a b c

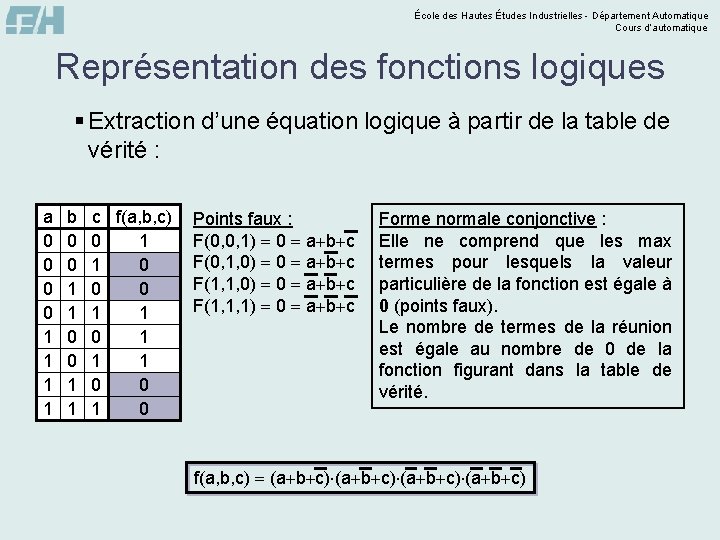
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Extraction d’une équation logique à partir de la table de vérité : a 0 0 1 1 b 0 0 1 1 c f(a, b, c) 0 1 0 0 1 1 1 0 0 1 0 Points faux : F(0, 0, 1) 0 a b c F(0, 1, 0) 0 a b c F(1, 1, 1) 0 a b c Forme normale conjonctive : Elle ne comprend que les max termes pour lesquels la valeur particulière de la fonction est égale à 0 (points faux). Le nombre de termes de la réunion est égale au nombre de 0 de la fonction figurant dans la table de vérité. f(a, b, c) (a b c)

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Exercice 1 : w Extraire les équations logiques des tables de vérité des fonctions suivantes : – 1ère forme canonique de la fonction f 7 – 2ème forme canonique de la fonction f 1 – 1ère forme et 2ème forme canonique de la fonction f 6 – 1ère forme et 2ème forme canonique de la fonction f 9 w En utilisant les règles de l’algèbre de Boole, simplifier ces fonctions.

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Exercice 2 : w Mêmes questions que l’exercice 1 en utilisant la table de vérité suivante : a 0 0 1 1 b 0 0 1 1 c f(a, b, c) 0 0 1 0 0 0 1 1 1

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Construction de la table de vérité à partir d’une équation logique : w Compter le nombre de variables différentes dans l’équation et créer la table de vérité. w 1ère méthode : pour chacune des combinaisons de la table de vérité, évaluer l’équation et reporter le résultat dans la table. w 2ème méthode : mettre l’équation sous une forme technologique et pour chacun des termes de la forme choisie, reporter les 1 ou les 0 dans les cases correspondantes de la table de vérité (plusieurs reports par terme). w 3ème méthode : mettre l’équation sous une forme canonique et pour chacun des termes de la forme choisie, reporter les 1 ou les 0 dans les cases correspondantes de la table de vérité (un seul report par terme).

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Exemple : w F(a, b) a b c w 3 variables a, b et c w F(a, b) a b c w F(a, b) a b c a (b c) w F(a, b) a b c a b a c a 0 0 1 1 b c f(a, b, c) 00 0 0 1 11 1 0 01 1 10 0 1 w F(a, b) a b c a b a c w F(a, b) a b c a b (c c) a c (b b) w F(a, b) a b c a b c w F(a, b) a b c

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques Les formes numériques § Chaque combinaison est repérée par un numéro (en général, l’équivalent décimal) afin de condenser l’écriture. Exemple précédent : F(a, b, c) ∑ (3, 4, 5, 6) F(a, b, c) ∏ (0, 1, 2, 7) Les logigrammes § C’est une association des symboles utilisés pour représenter les fonctions logiques en vue de leur réalisation câblée ou programmée. § Le logigramme le plus simple est celui qui utilise le moins d’opérateurs possible et de même type.

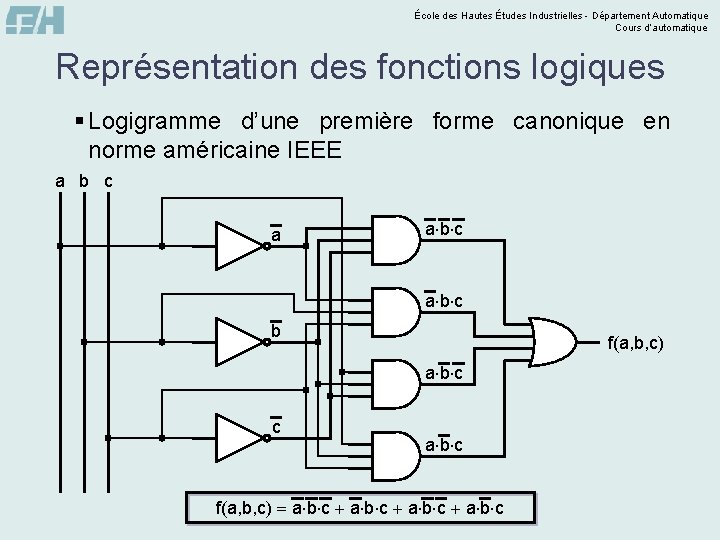
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Logigramme d’une première forme canonique en norme américaine IEEE a b c b f(a, b, c) a b c c a b c f(a, b, c) a b c

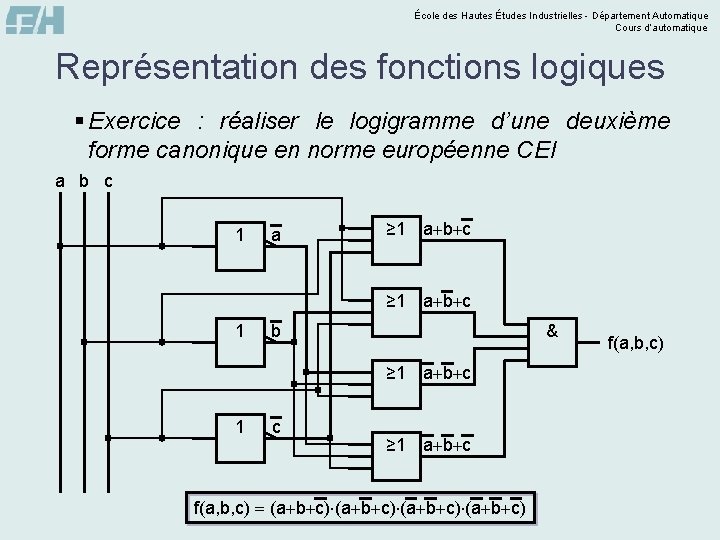
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Exercice : réaliser le logigramme d’une deuxième forme canonique en norme européenne CEI a b c 1 a ≥ 1 a b c 1 & b ≥ 1 a b c 1 c ≥ 1 a b c f(a, b, c) (a b c) f(a, b, c)

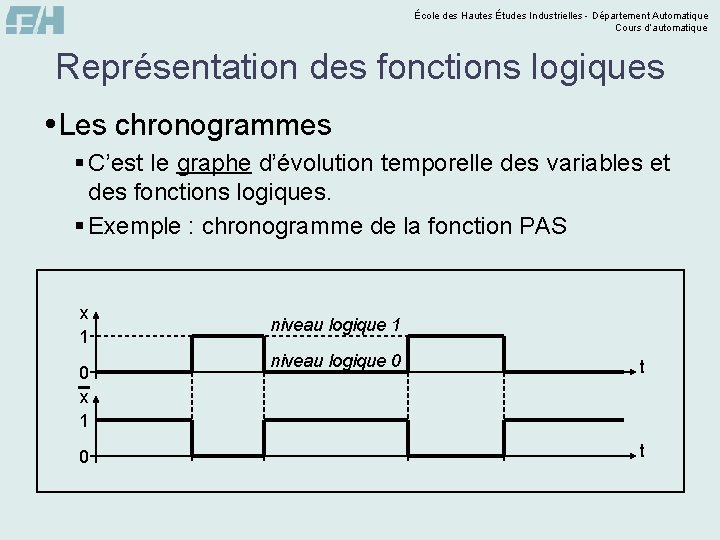
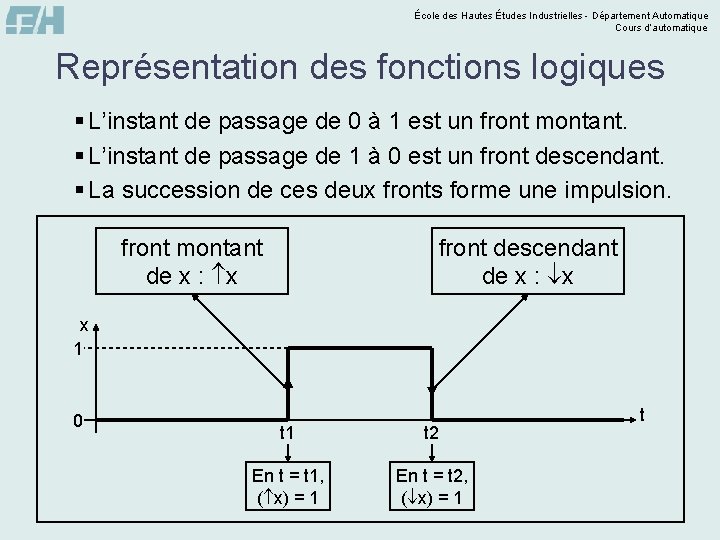
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques Les chronogrammes § C’est le graphe d’évolution temporelle des variables et des fonctions logiques. § Exemple : chronogramme de la fonction PAS x 1 0 niveau logique 1 niveau logique 0 t t

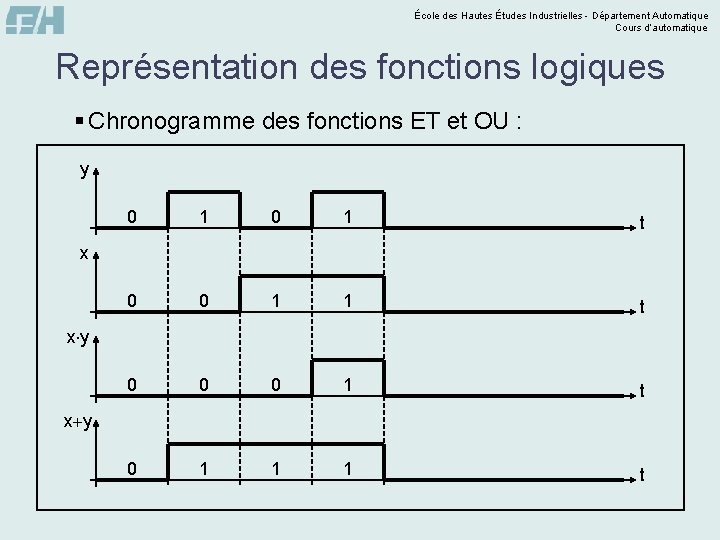
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Chronogramme des fonctions ET et OU : y 0 1 t 0 0 1 1 t 0 0 0 1 t 0 1 1 1 t x x y

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § L’instant de passage de 0 à 1 est un front montant. § L’instant de passage de 1 à 0 est un front descendant. § La succession de ces deux fronts forme une impulsion. front montant de x : x front descendant de x : x x 1 0 t 1 t 2 En t = t 1, ( x) = 1 En t = t 2, ( x) = 1 t

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques § Propriétés : w a a w ( a) x ( a) y ( a) (x y) w ( a) x ( b) x x ( a b) w a b (a b) w a a § Exercice : w Compléter les chronogrammes du polycopié afin d’illustrer les propriétés précédentes.

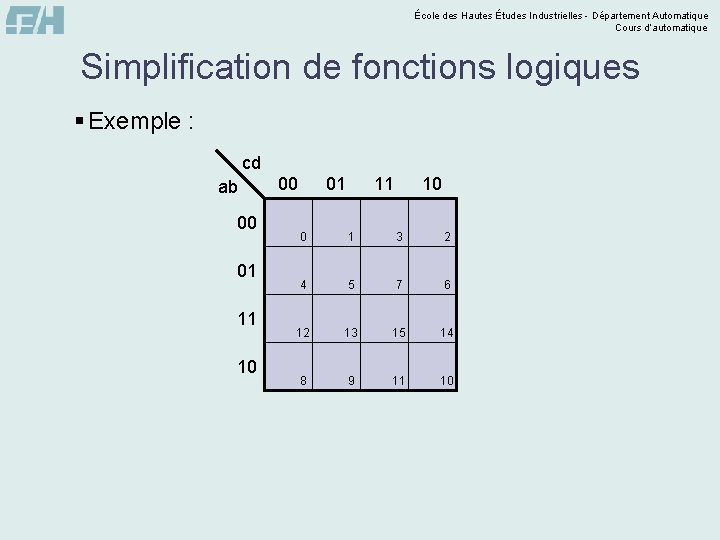
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques Les tableaux de Karnaugh § Soit F, une fonction de n variables. § Le tableau de Karnaugh est un tableau de 2 n cases correspondant aux 2 n combinaisons d’entrée dans lesquelles sont notées les valeurs correspondantes de la fonction. a 0 0 1 1 b 0 0 1 1 c f(a, b, c) 0 0 1 1 0 0 0 1 1 bc 01 00 a 0 0 1 1 0 4 1 0 11 1 5 0 1 10 3 7 1 0 tableau de Karnaugh 2 6 Le passage d’une case à une case voisine se fait par changement de la valeur d’une seule variable à la fois (code binaire réfléchi ou code de Gray).

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Représentation des fonctions logiques Exercice : § Réaliser le tableau de Karnaugh de la fonction f de 4 variables a, b, c et d définie par la table de vérité suivante : cd ab 00 00 0 01 1 11 0 10 1 01 0 4 12 8 1 0 11 1 5 13 9 0 1 10 3 7 15 11 1 0 2 6 14 10 a 0 0 0 0 1 1 1 1 b 0 0 0 0 1 1 1 1 c 0 0 1 1 d 0 1 0 1 f 0 1 1 0 0 1 1 0

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques Méthode algébrique : application des principes de l’algèbre de Boole § mise en facteur ou développement § idempotence. . . Méthode graphique : utilisation des tableaux de Karnaugh § Deux cases sont adjacentes si le passage de l’une à l’autre se fait uniquement par le changement d’état d’une seule variable. § Ce principe s’applique également pour des ensembles de cases adjacentes constitués de 2 n cases.

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques § Exemple : cd ab 00 01 11 10 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques § Méthode de Karnaugh : w Selon la forme recherchée, regrouper les cases adjacentes de même valeur (soit 0, soit 1) par des ensembles plus grands possibles et correspondant à des puissances de 2. Tous ces regroupements correspondent à des monômes premiers (ou monaux) et constitue la base première complète. La somme de ces monômes donne une expression simplifiée de la fonction logique mais pas sa forme minimale. w La forme minimale est obtenue en faisant la somme des monômes premiers principaux (irredondants), c’est à dire un regroupement dans lequel il existe au moins une case qui ne peut être regroupée que par elle-même. Parfois, plusieurs possibilité sont offertes et on obéira aux règles suivantes : w Tous les 1 (ou tous les 0) doivent être regroupés au moins une fois. w Les regroupements les plus grands doivent être choisis en priorité. w Les cases à regrouper doivent l’être un minimum de fois (commencer par celles qui n’ont qu’une seule façon de se regrouper).

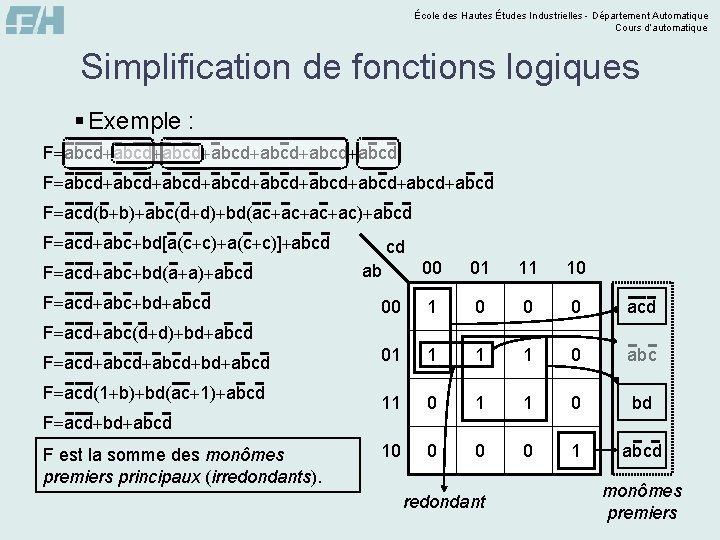
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques § Exemple : F abcd abcd abcd abcd F acd(b b) abc(d d) bd(ac ac) abcd F acd abc bd[a(c c)] abcd F acd abc bd(a a) abcd F acd abc bd abcd cd 00 01 11 10 00 1 0 0 0 acd 01 1 0 abc 11 0 1 1 0 bd 10 0 1 abcd ab F acd abc(d d) bd abcd F acd abcd bd abcd F acd(1 b) bd(ac 1) abcd F acd bd abcd F est la somme des monômes premiers principaux (irredondants). redondant monômes premiers

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques § Exercice : w Simplifier sous une 1ére et 2ème forme technologique la fonction définie par la table de vérité suivante en utilisant la méthode de Karnaugh : a 0 0 1 1 b 0 0 1 1 c f(a, b, c) 0 0 1 0 0 0 1 1 1

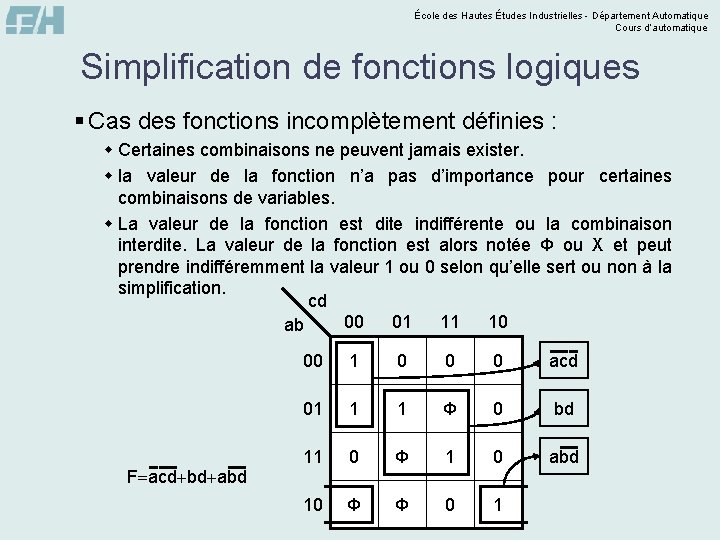
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques § Cas des fonctions incomplètement définies : w Certaines combinaisons ne peuvent jamais exister. w la valeur de la fonction n’a pas d’importance pour certaines combinaisons de variables. w La valeur de la fonction est dite indifférente ou la combinaison interdite. La valeur de la fonction est alors notée Φ ou X et peut prendre indifféremment la valeur 1 ou 0 selon qu’elle sert ou non à la simplification. cd 00 01 11 10 ab 00 1 0 0 0 acd 01 1 1 Φ 0 bd 11 0 Φ 1 0 abd 10 Φ Φ 0 1 F acd bd abd

École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques § Exercice : w Simplifier sous une 1ére forme technologique la fonction suivante en utilisant la méthode de Karnaugh : cde 000 001 010 111 100 ab 00 1 1 0 1 01 1 0 0 0 1 11 1 0 0 0 1 10 1 1 1

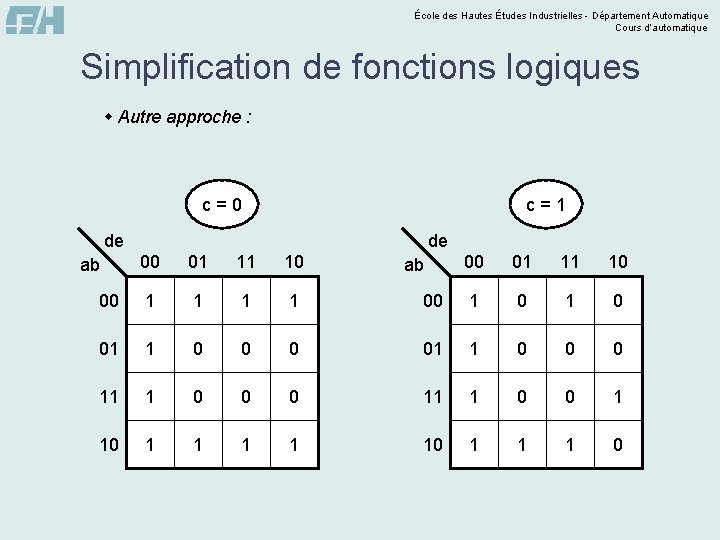
École des Hautes Études Industrielles - Département Automatique Cours d’automatique Simplification de fonctions logiques w Autre approche : c=0 c=1 de de 00 01 11 10 00 1 1 01 1 0 0 11 1 0 10 1 1 ab 00 01 11 10 00 1 0 0 01 1 0 0 0 11 1 0 0 1 10 1 1 1 0 ab