Charged particle Moving charge current Associated magnetic field

Charged particle

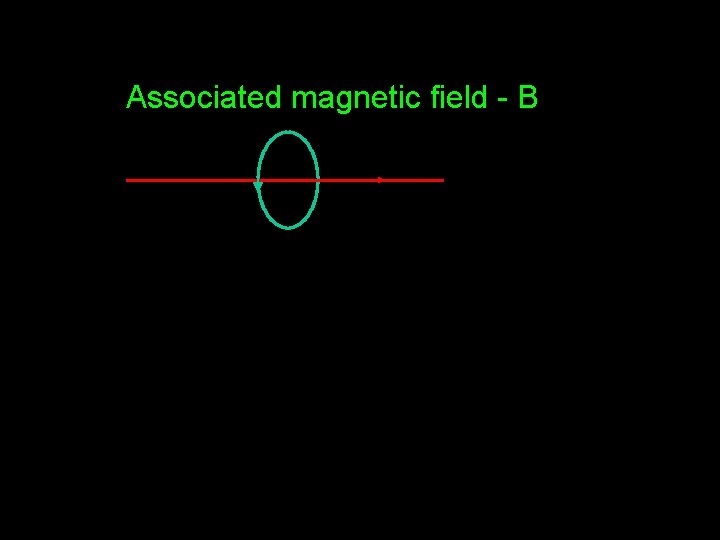
Moving charge = current

Associated magnetic field - B

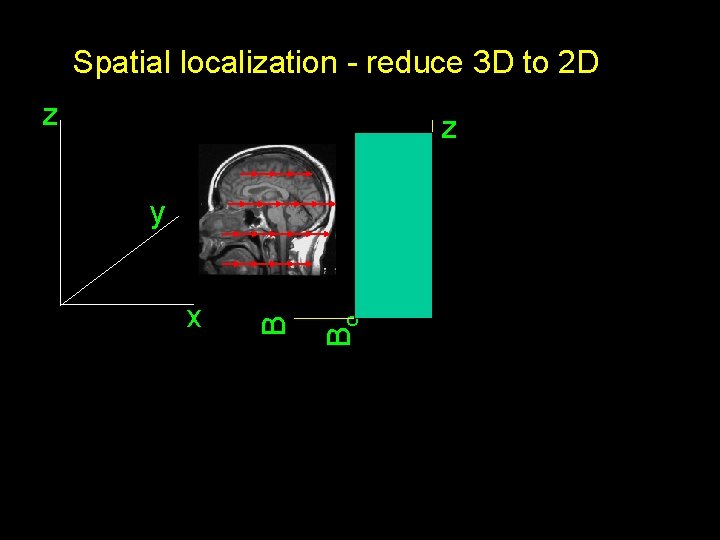
Macroscopic picture (typical dimensions (1 mm)3 ) Consider nucleus of hydrogen in H 2 O molecules: proton magnetization randomly aligned

Macroscopic picture (typical dimensions (1 mm)3 ) Apply static magnetic field: proton magnetization either aligns with or against magnetic field Bo M

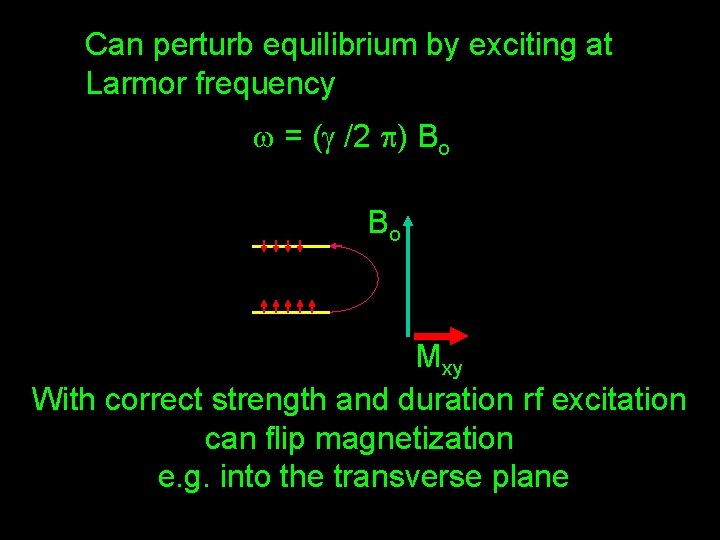
Macroscopic picture (typical dimensions (1 mm)3 ) Can perturb equilibrium by exciting at Larmor frequency w = (g /2 p) Bo

Can perturb equilibrium by exciting at Larmor frequency w = (g /2 p) Bo Bo Mxy With correct strength and duration rf excitation can flip magnetization e. g. into the transverse plane

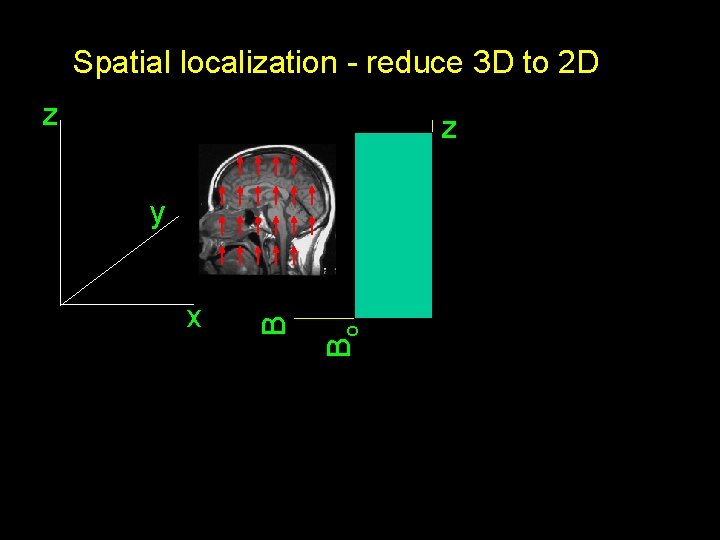
Spatial localization - reduce 3 D to 2 D z z Bo x B y

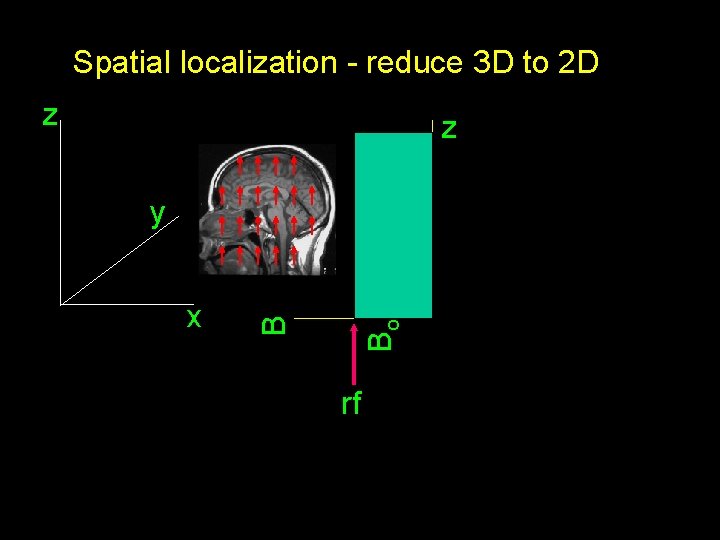
Spatial localization - reduce 3 D to 2 D z z Bo x B y rf

Spatial localization - reduce 3 D to 2 D z z Bo x B y

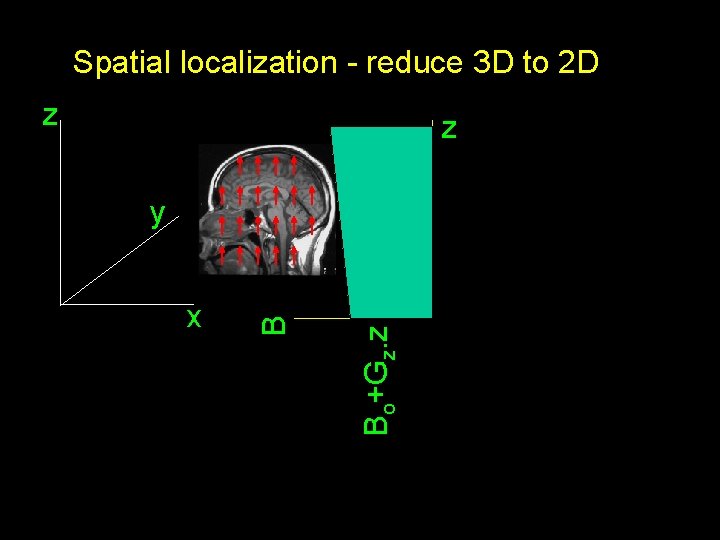
Spatial localization - reduce 3 D to 2 D z z Bo+Gz. z x B y

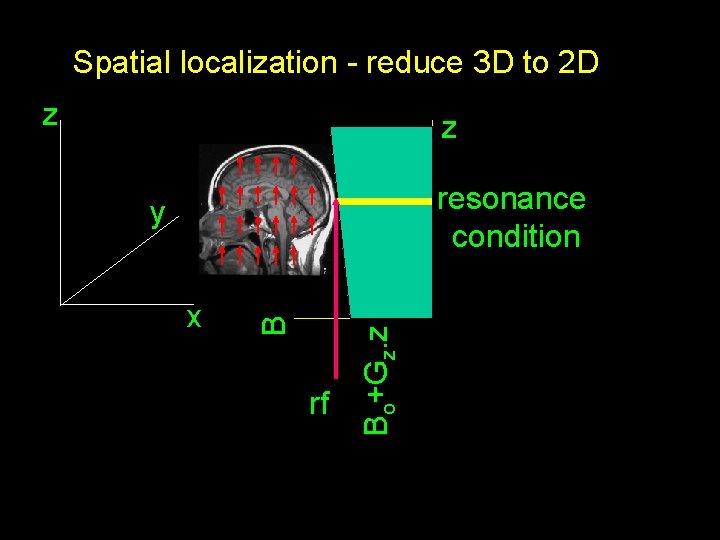
Spatial localization - reduce 3 D to 2 D z z resonance condition rf Bo+Gz. z x B y

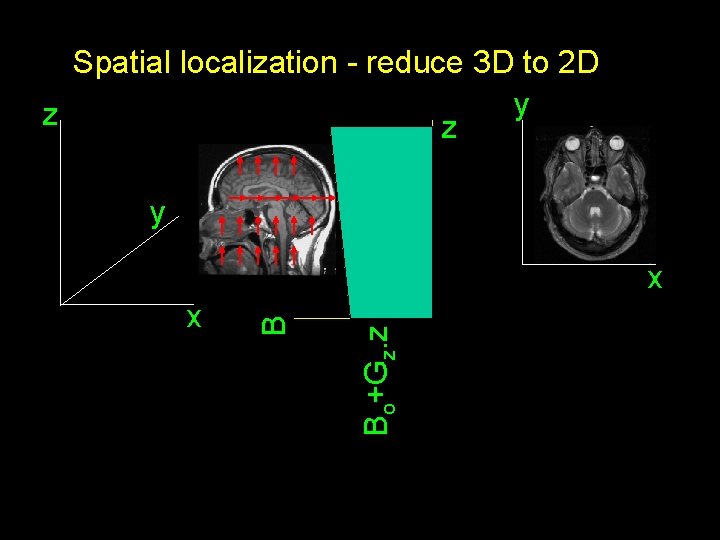
Spatial localization - reduce 3 D to 2 D y z z y Bo+Gz. z x B x

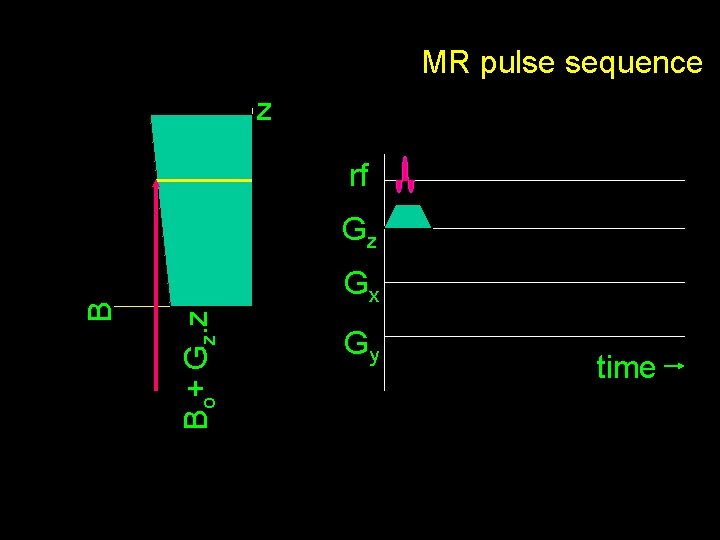
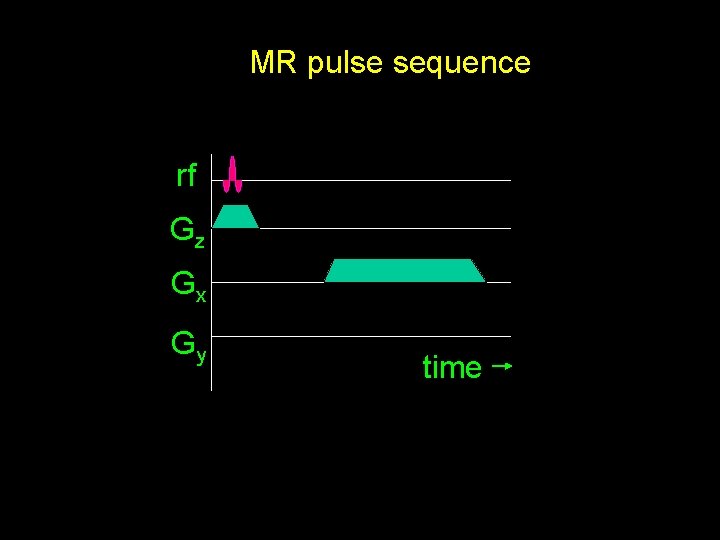
MR pulse sequence z rf Gx Bo+ Gz. z B Gz Gy time

Spatial localization - e. g. , in 1 d what is r(x) ? Once magnetization is in the transverse plane it precesses at the Larmor frequency w = 2 p/g B(x) M(x, t) = Mo r(x) exp(-i. g. f(x, t)) If we apply a linear gradient, Gx , of magnetic field along x the accumulated phase at x after time t will be: t f(x, t) = ∫o x Gx(t') dt' (ignoring carrier term) f

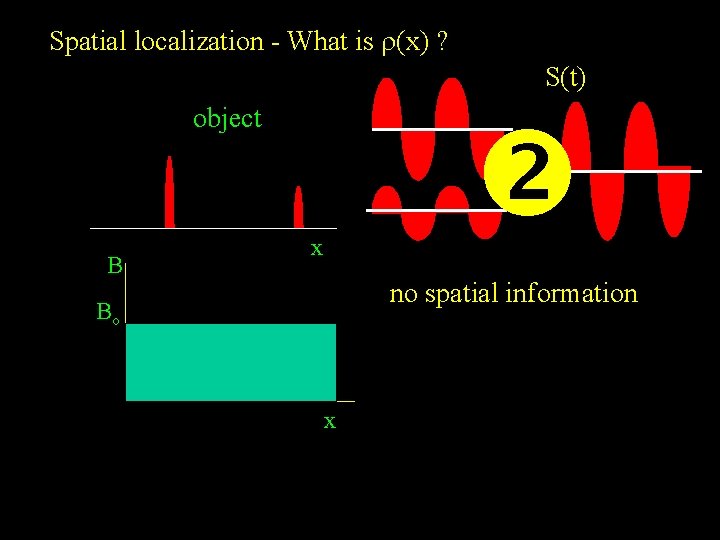
Spatial localization - What is r(x) ? S(t) object B x no spatial information Bo xx

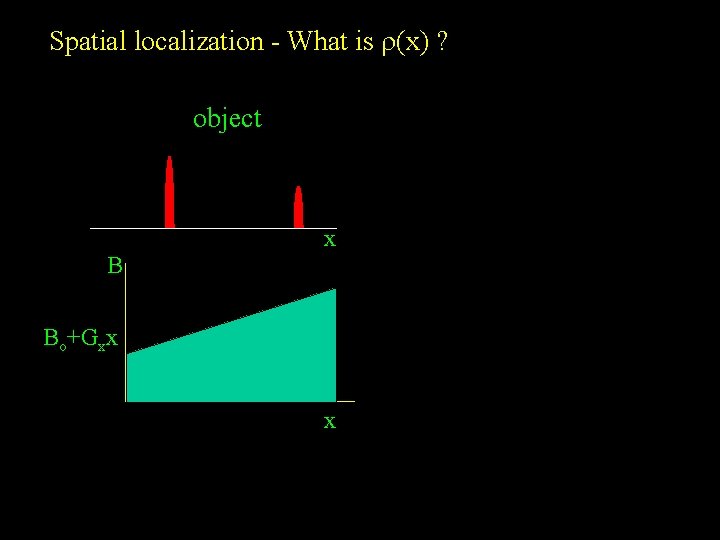
Spatial localization - What is r(x) ? object B xx Bo+Gxx xx

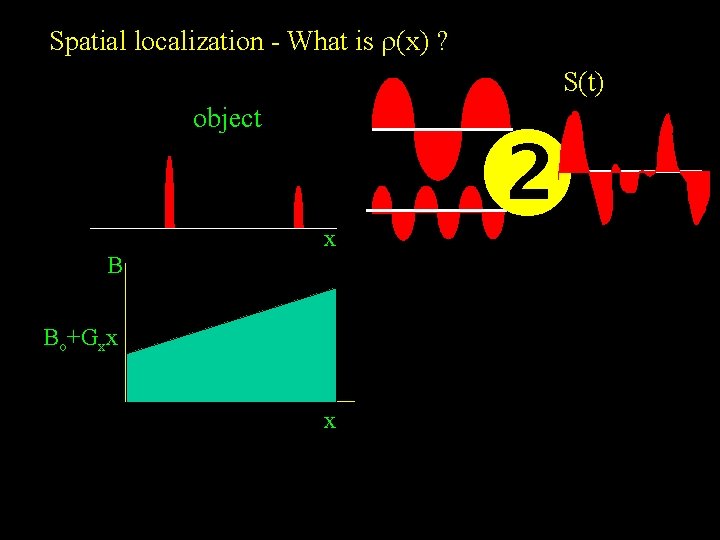
Spatial localization - What is r(x) ? S(t) object B xx Bo+Gxx xx

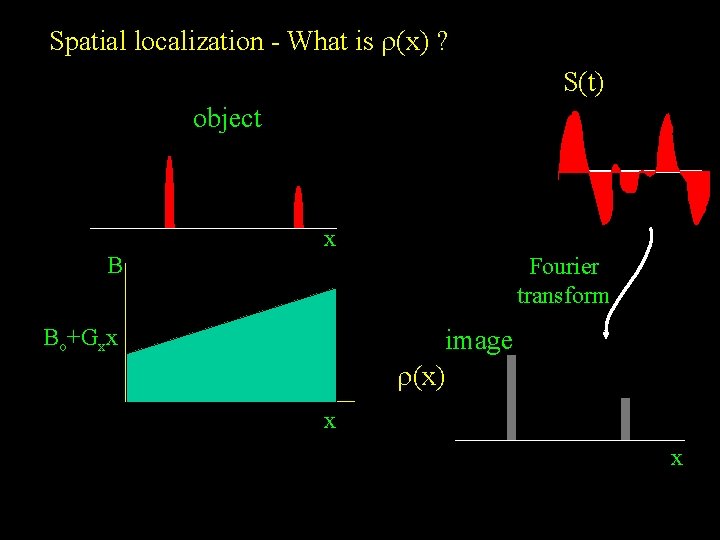
Spatial localization - What is r(x) ? S(t) object B xx Fourier transform Bo+Gxx image r(x) xx x

For an antenna sensitive to all the precessing magnetization, the measured signal is: S(t) = ∫ M(x, t) dx = Mo ∫ r(x) exp (-i. (g. Gx) x. t) dx therefore: r(x) = ∫ M(x, t) dx = Mo ∫ S(t) exp (i. c. x. t) dt

MR pulse sequence rf Gz Gx Gy time

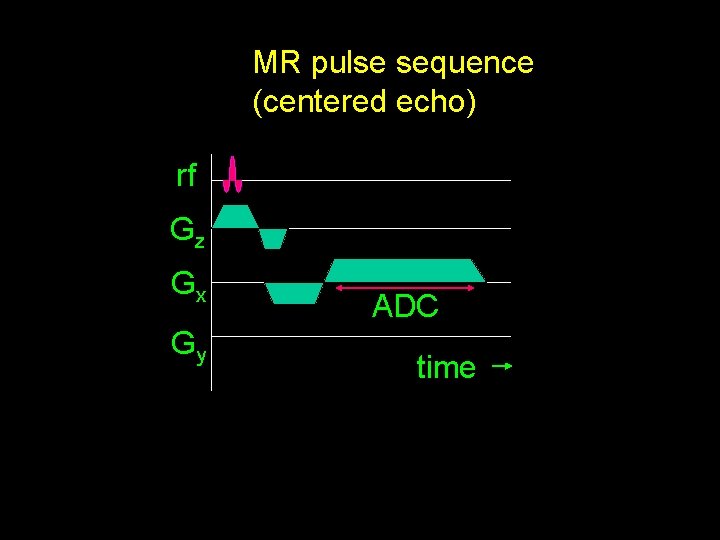
For NMR in a magnet with imperfect homogeneity, spin coherence is lost because of spatially varying precession Hahn (UC Berkeley)showed that this could be reversed by flipping the spins through 180° the spin echo In MRI, spatially varying fields are applied to provide spatial localization - these spatially varying magnetic fields must also be compensated - the gradient echo

MR pulse sequence (centered echo) rf Gz Gx Gy ADC time

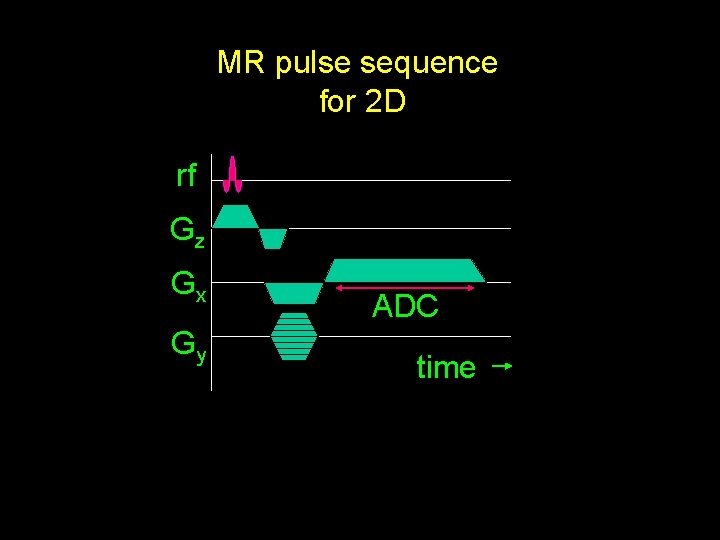
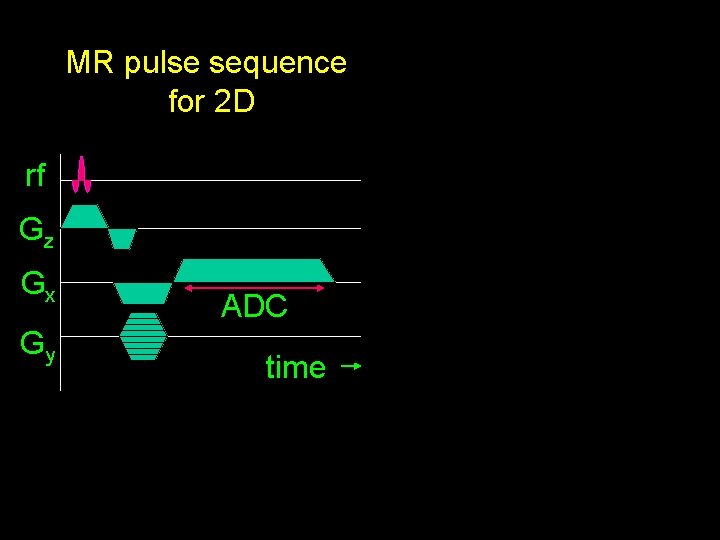
MR pulse sequence for 2 D rf Gz Gx Gy ADC time

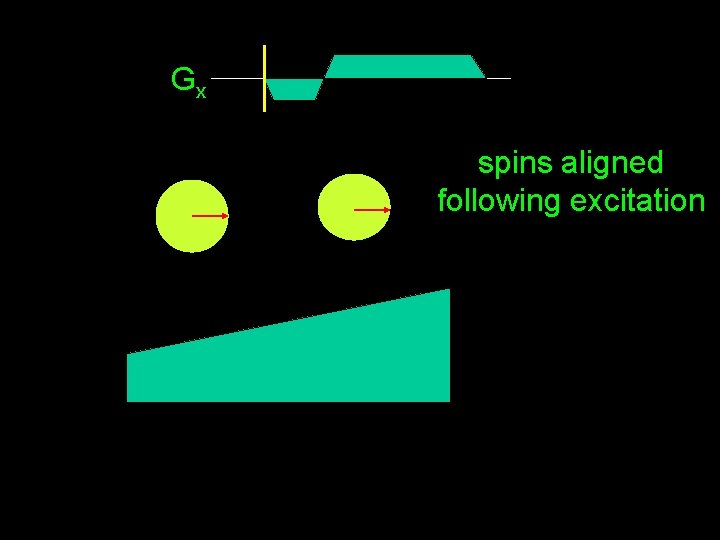
Gx spins aligned following excitation

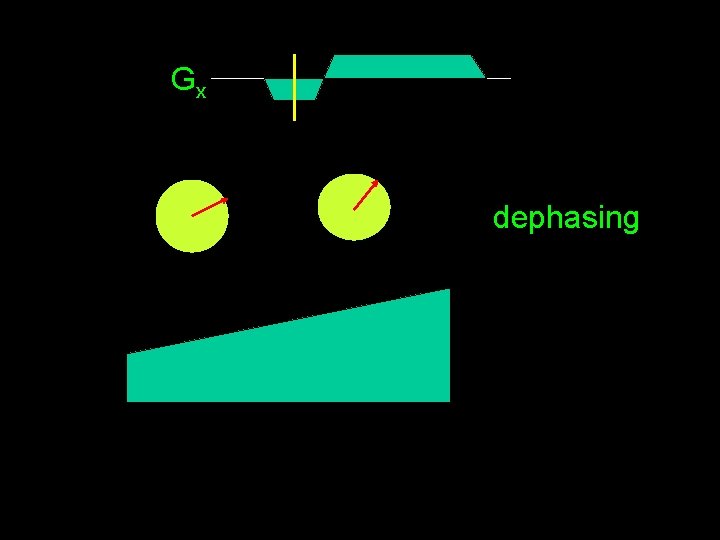
Gx dephasing

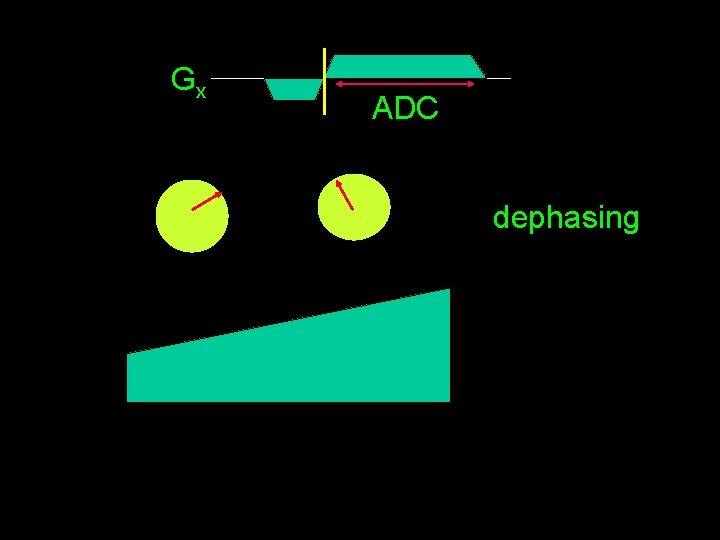
Gx ADC dephasing

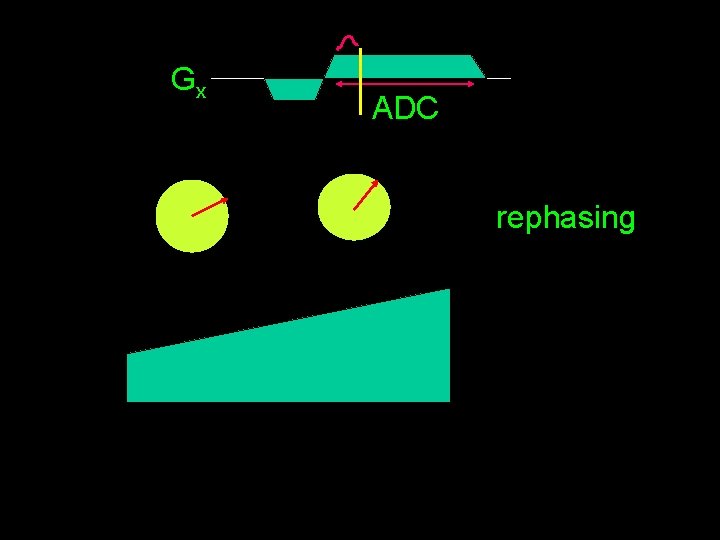
Gx ADC rephasing

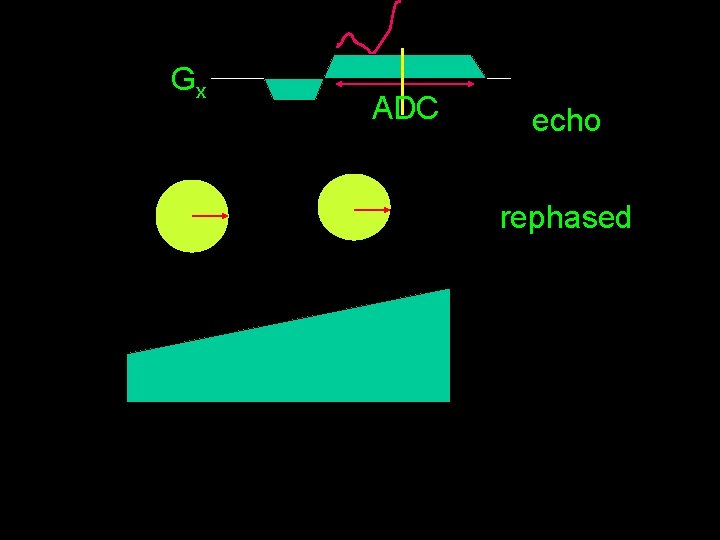
Gx ADC echo rephased

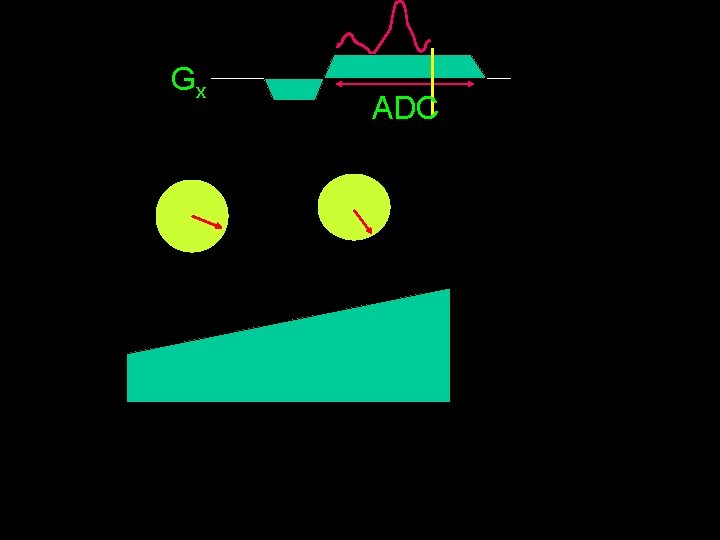
Gx ADC

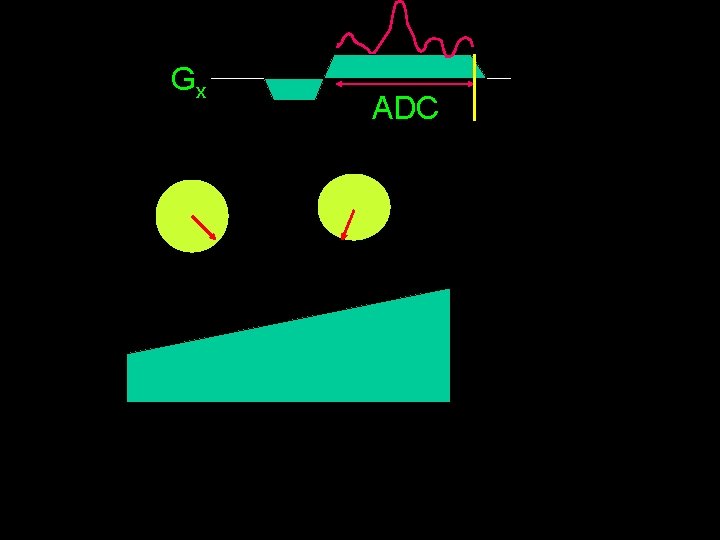
Gx ADC

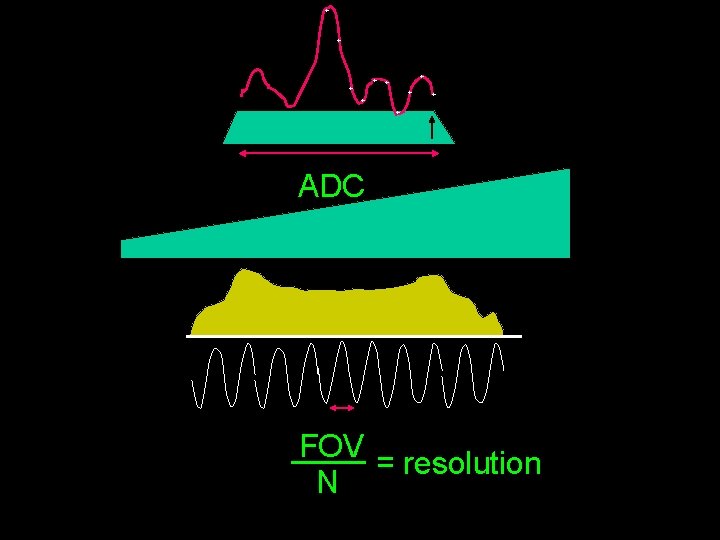
+ + + + + ADC FOV = resolution N

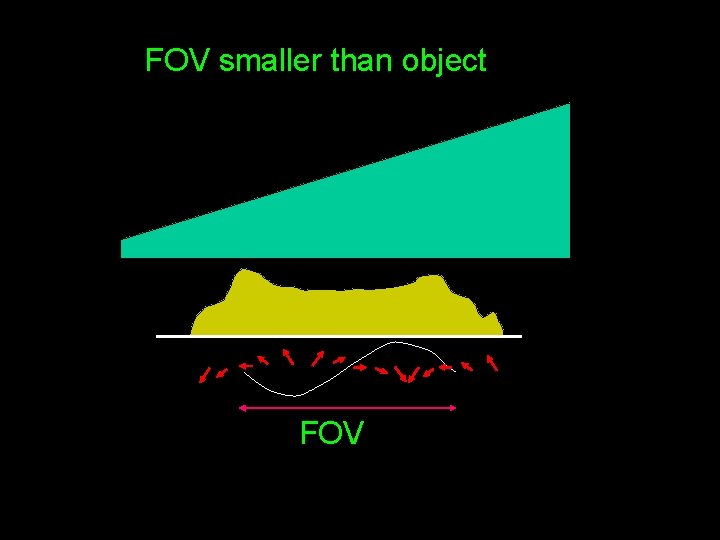
FOV smaller than object FOV

FOV

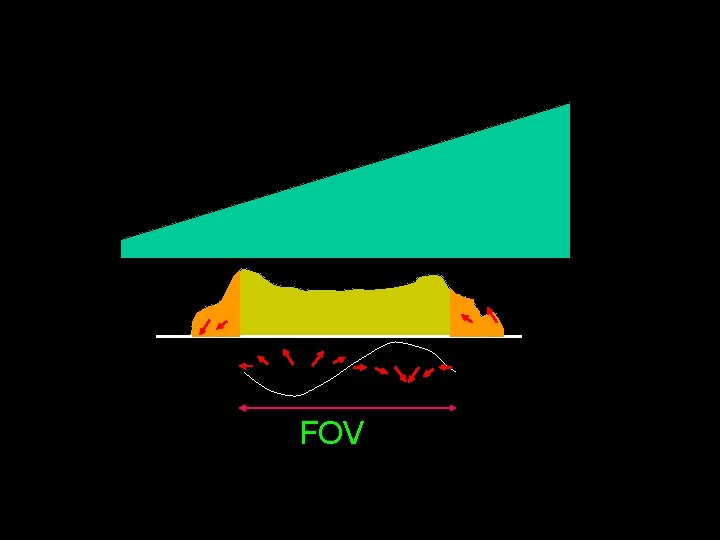
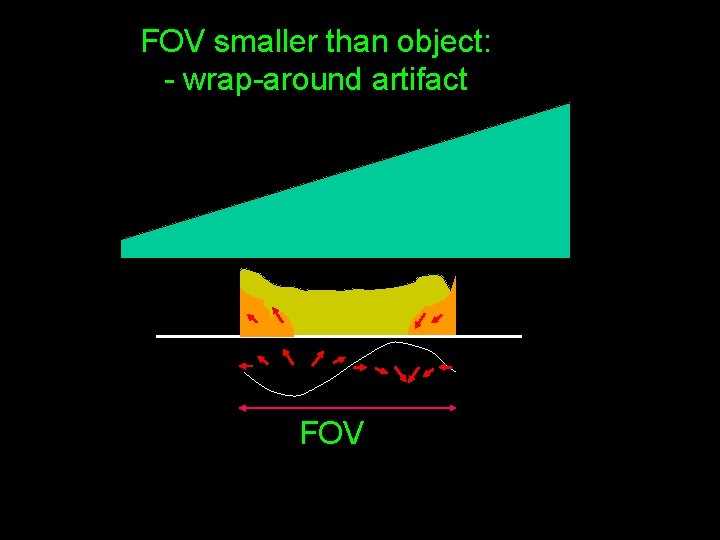
FOV smaller than object: - wrap-around artifact FOV

MR pulse sequence for 2 D rf Gz Gx Gy ADC time

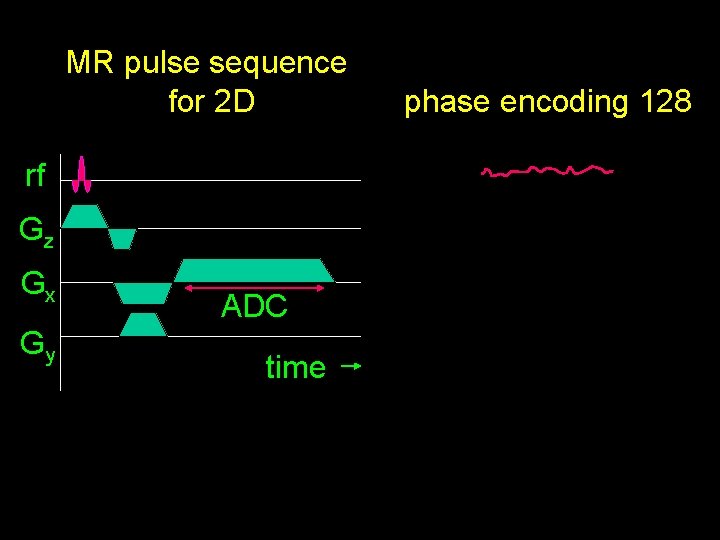
MR pulse sequence for 2 D rf Gz Gx Gy ADC time phase encoding 128

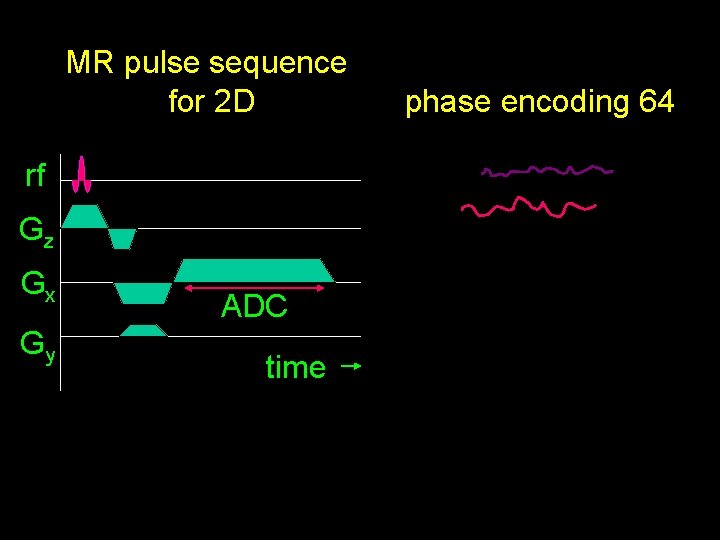
MR pulse sequence for 2 D rf Gz Gx Gy ADC time phase encoding 64

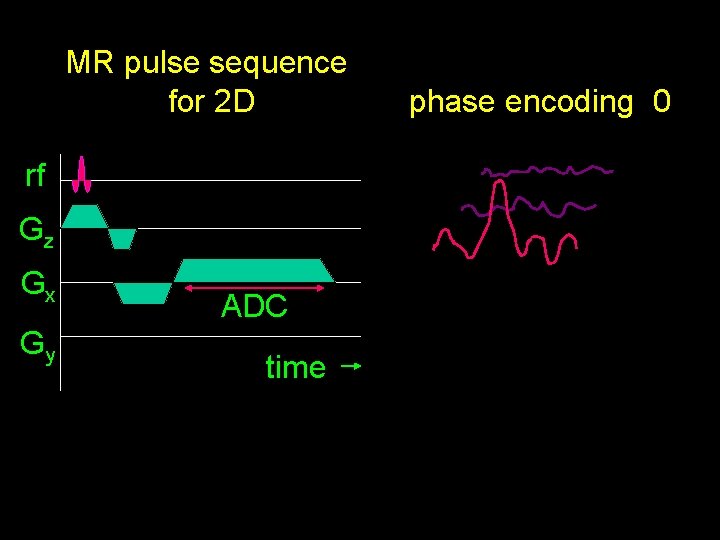
MR pulse sequence for 2 D rf Gz Gx Gy ADC time phase encoding 0

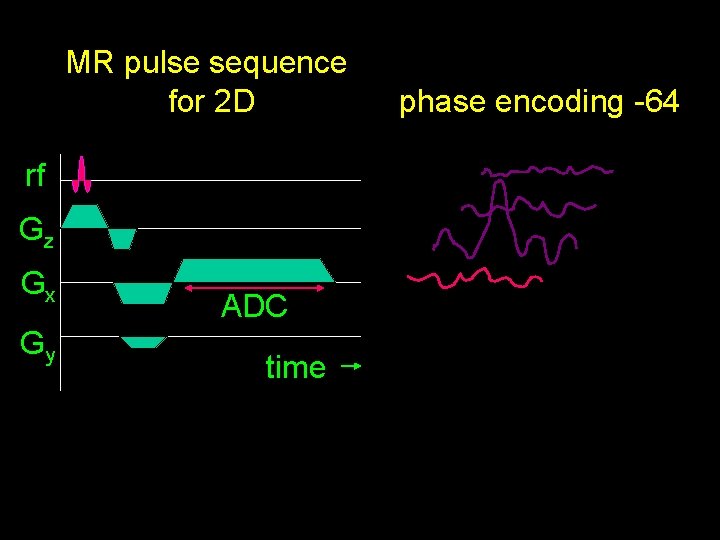
MR pulse sequence for 2 D rf Gz Gx Gy ADC time phase encoding -64

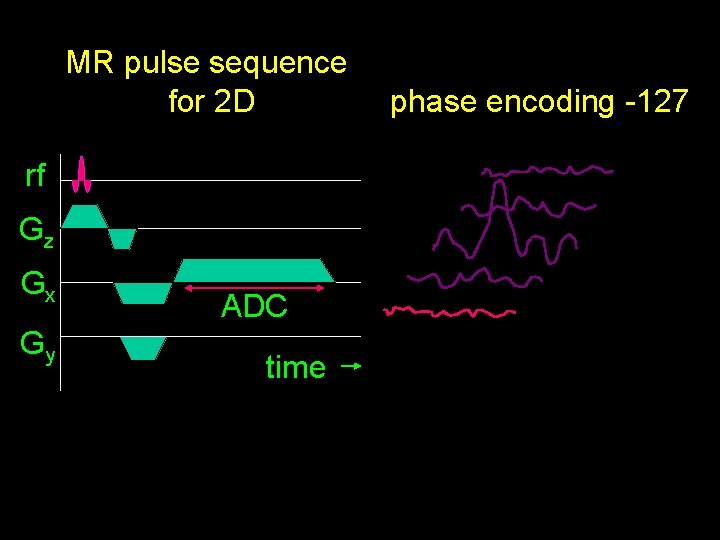
MR pulse sequence for 2 D rf Gz Gx Gy ADC time phase encoding -127

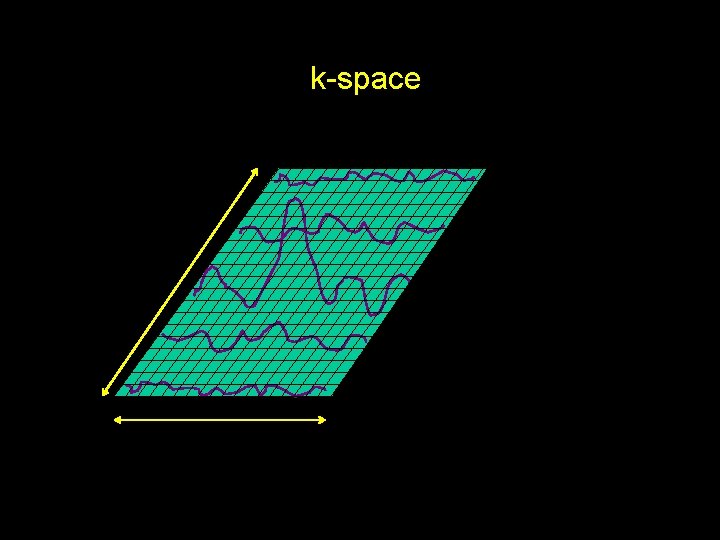
k-space

Fourier

Fourier transform(ed)

inner k-space Fourier transform overall contrast information

outer k-space Fourier transform edge information