Magnetic Flux Unit for flux is weber The

Magnetic Flux • Unit for flux is weber • The definition of 1 weber is the amount of flux that can produce an induced voltage of 1 V in a one turn coil if the flux reduce to zero with uniform rate. Magnetic Flux density B • Unit for magnetic flux density is Tesla • The definition of 1 tesla is the flux density that can produce a force of 1 Newton per meter acting upon a conductor carrying 1 ampere of current. Magnetic field strength H • Unit for magnetic field strength is Ampere/m • A line of force that produce flux

F = B l I newton Where F = force ; B = magnetic flux density ; l =the length of conductor and I = current in the conductor Where = magnetic flux ; B = magnetic flux density and A = area of cross-section Where H = magnetic field strength ; B = magnetic flux density and = permeability of the medium Permeability in free space o = B/H = 4 x 10 -7 H/m

Relative Permeability ( r) n Relative permeability is defined as a ratio of flux density produced in a material to the flux density produced in a vacuum for the same magnetic filed strength. Thus r = / o = r o = B/H or B = r o. H

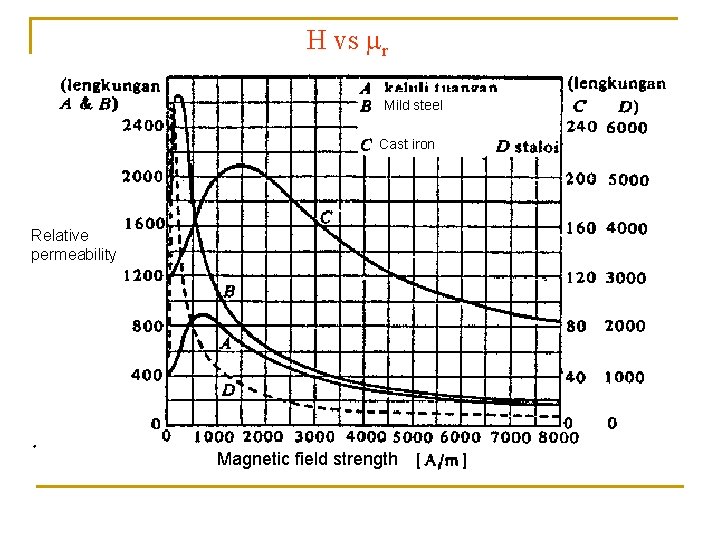
H vs r Mild steel Cast iron Relative permeability Magnetic field strength

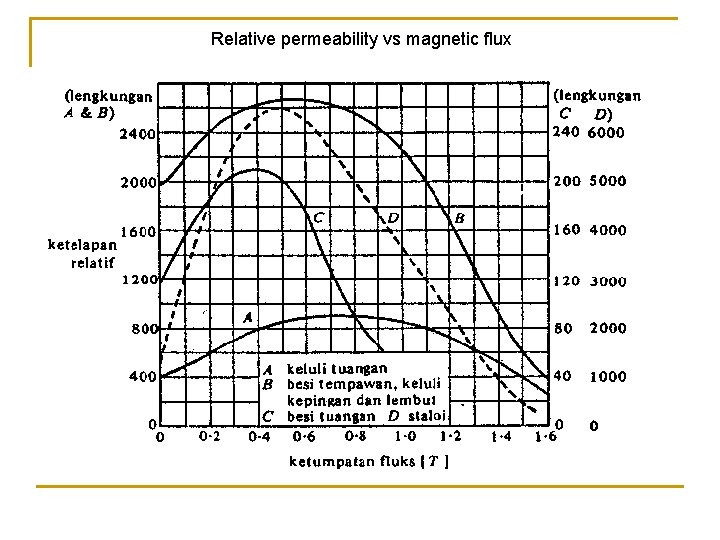
Relative permeability vs magnetic flux

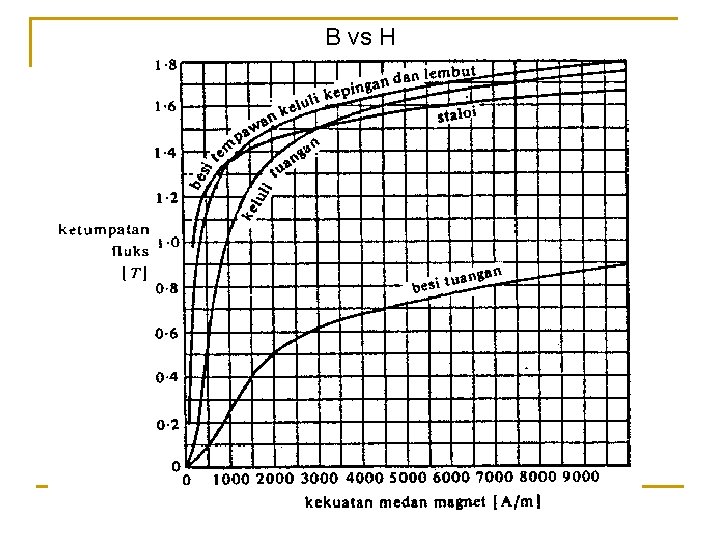
B vs H

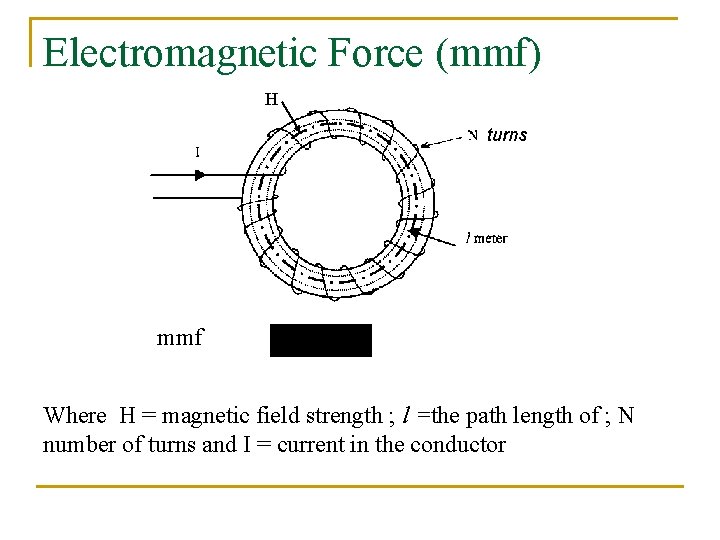
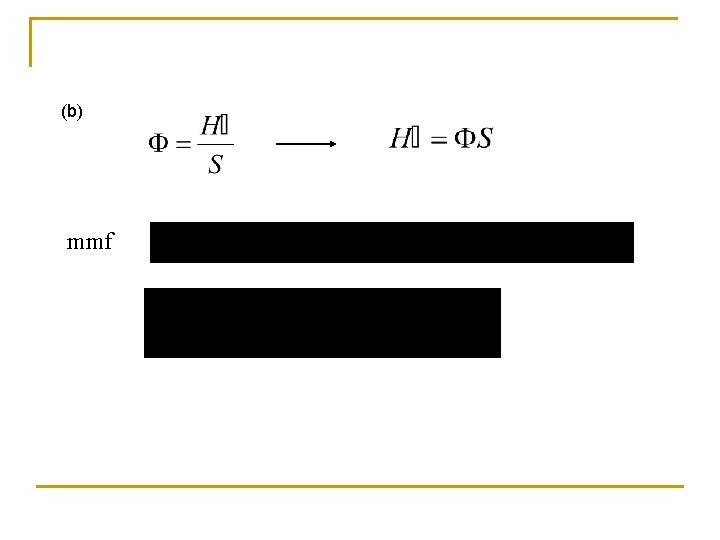
Electromagnetic Force (mmf) H turns mmf Where H = magnetic field strength ; l =the path length of ; N number of turns and I = current in the conductor

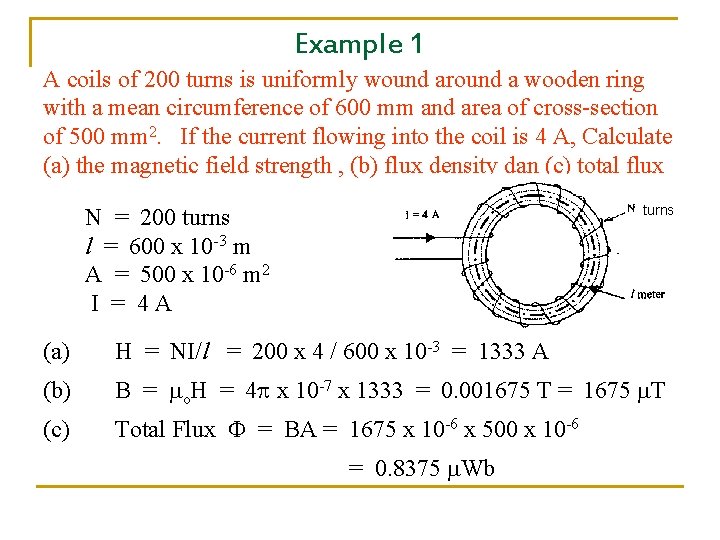
Example 1 A coils of 200 turns is uniformly wound around a wooden ring with a mean circumference of 600 mm and area of cross-section of 500 mm 2. If the current flowing into the coil is 4 A, Calculate (a) the magnetic field strength , (b) flux density dan (c) total flux turns N = 200 turns l = 600 x 10 -3 m A = 500 x 10 -6 m 2 I = 4 A (a) H = NI/l = 200 x 4 / 600 x 10 -3 = 1333 A (b) B = o. H = 4 x 10 -7 x 1333 = 0. 001675 T = 1675 T (c) Total Flux = BA = 1675 x 10 -6 x 500 x 10 -6 = 0. 8375 Wb

Reluctance ( S ) Ohm‘s law I = V/R [A] Where I =current; V=voltage and R=resistance And the resistance can be relate to physical parameters as R = l /A ohm Where =resistivity [ohm-meter], l= length in meter and A=area of cross-section [meter square] Analogy to the ohm‘s law V=NI=H l I= and R=S where

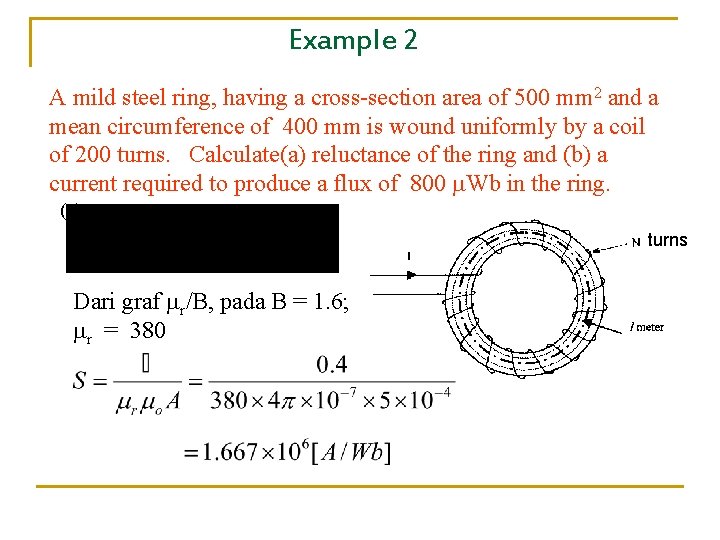
Example 2 A mild steel ring, having a cross-section area of 500 mm 2 and a mean circumference of 400 mm is wound uniformly by a coil of 200 turns. Calculate(a) reluctance of the ring and (b) a current required to produce a flux of 800 Wb in the ring. (a) turns Dari graf r/B, pada B = 1. 6; r = 380

(b) mmf

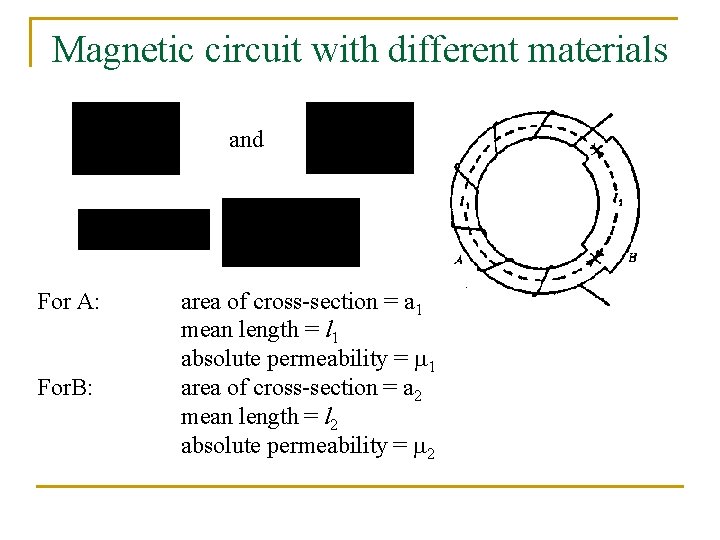
Magnetic circuit with different materials and For A: For. B: area of cross-section = a 1 mean length = l 1 absolute permeability = 1 area of cross-section = a 2 mean length = l 2 absolute permeability = 2

Mmf for many materials in series total mmf = HAl. A + HBl. B HA =magnetic strength in material A l. A=mean length of material A HB =magnetic strength in material B l. B=mean length of material B In general (m. m. f) = Hl

Example 3 A magnetic circuit comprises three parts in series, each of uniform cross-section area(c. s. a). They are : (a)A length of 80 mm and c. s. a 50 mm 2; (b)A length of 60 mm and c. s. a 90 mm 2; (c)An airgap of length 0. 5 mm and c. s. a 150 mm 2. A coil of 4000 turns is wound on part (b), and the flux density in the airgap is 0. 3 T. Assuming that all the flux passes through the given circuit, and that the relative permeability r is 1300, estimate the coil current to produce such a flux density.

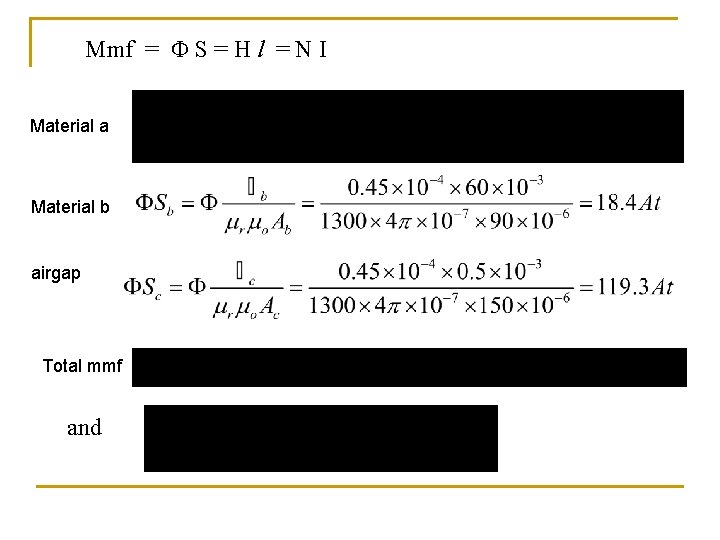
Mmf = S = H l = N I Material a Material b airgap Total mmf and

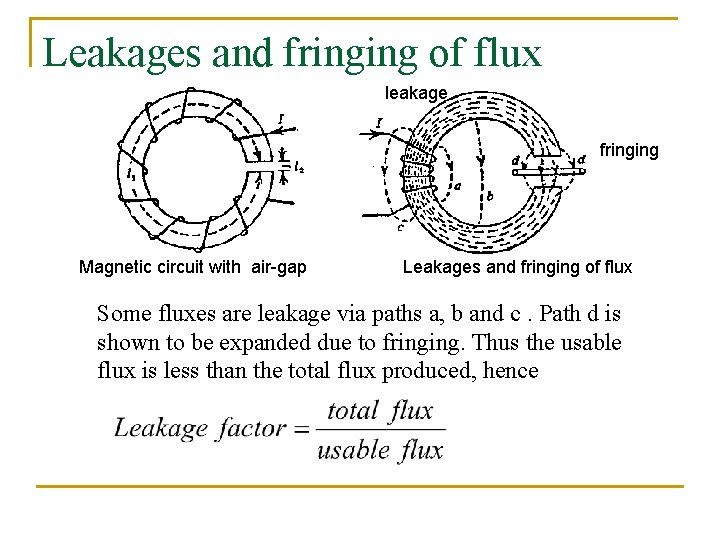
Leakages and fringing of flux leakage fringing Magnetic circuit with air-gap Leakages and fringing of flux Some fluxes are leakage via paths a, b and c. Path d is shown to be expanded due to fringing. Thus the usable flux is less than the total flux produced, hence

Example 4 A magnetic circuit as in Figure is made from a laminated steel. The breadth of the steel core is 40 mm and the depth is 50 mm, 8% of it is an insulator between the laminatings. The length and the area of the airgap are 2 mm and 2500 mm 2 respectively. A coil is wound 800 turns. If the leakage factor is 1. 2, calculate the current required to magnetize the steel core in order to produce flux of 0. 0025 Wb across the airgap.

92% of the depth is laminated steel, thus the area of cross section is AS = 40 x 50 x 0. 92 = 1840 mm 2=0. 00184 m

From the B-H graph, at B=1. 63 T, H=4000 AT/m mmf in the steel core = Hl = 4000 x 0. 6 = 2400 AT Total mmf. = 1592 + 2400 = 3992 AT NI = 3992/800 = 5 A

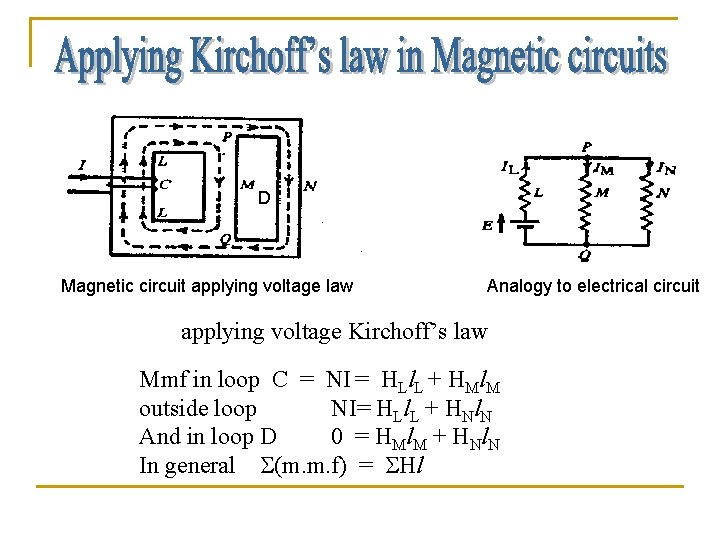
D Magnetic circuit applying voltage law Analogy to electrical circuit applying voltage Kirchoff’s law Mmf in loop C = NI = HLl. L + HMl. M outside loop NI= HLl. L + HNl. N And in loop D 0 = H Ml M + H Nl N In general (m. m. f) = Hl

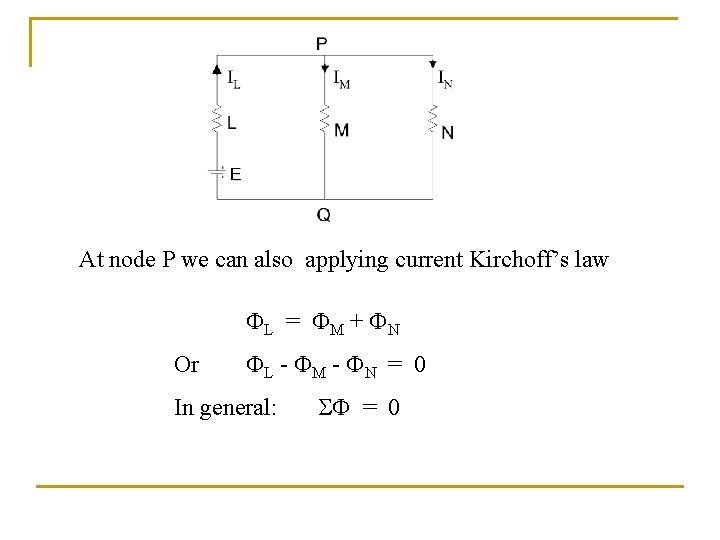
At node P we can also applying current Kirchoff’s law L = M + N Or L - M - N = 0 In general: = 0

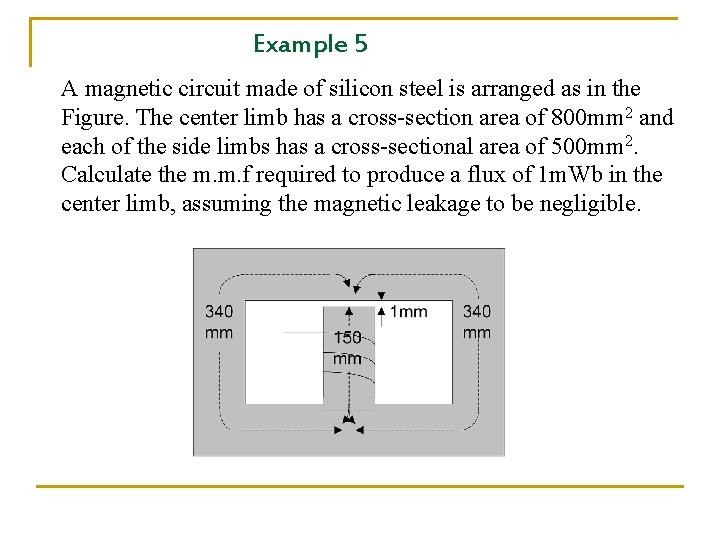
Example 5 A magnetic circuit made of silicon steel is arranged as in the Figure. The center limb has a cross-section area of 800 mm 2 and each of the side limbs has a cross-sectional area of 500 mm 2. Calculate the m. m. f required to produce a flux of 1 m. Wb in the center limb, assuming the magnetic leakage to be negligible.

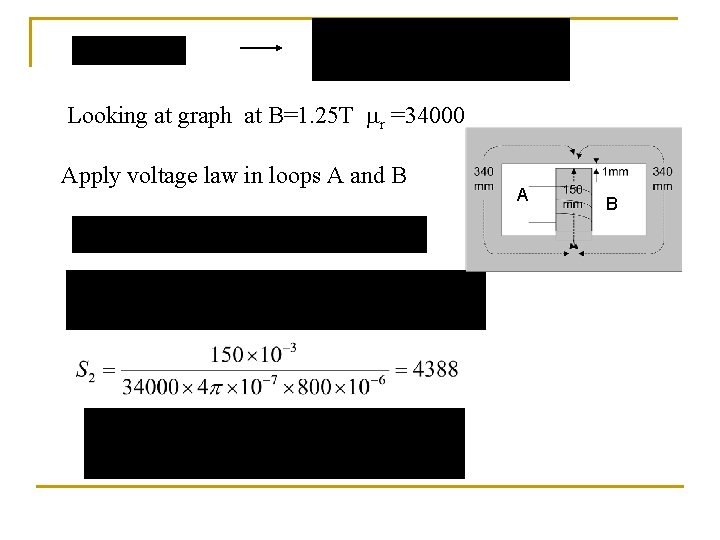
Looking at graph at B=1. 25 T r =34000 Apply voltage law in loops A and B A B

Since the circuit is symmetry A = B In the center limb , the flux is 1 m. Wb which is equal to 2 Therefore =0. 5 m. Wb A

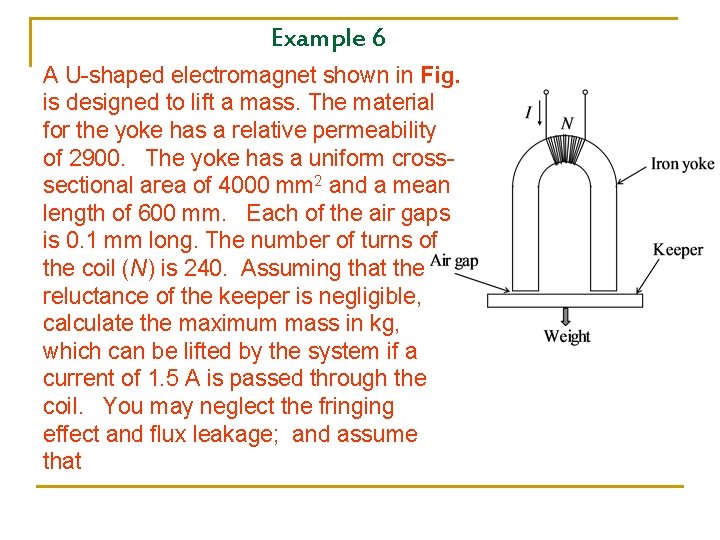
Example 6 A U-shaped electromagnet shown in Fig. is designed to lift a mass. The material for the yoke has a relative permeability of 2900. The yoke has a uniform crosssectional area of 4000 mm 2 and a mean length of 600 mm. Each of the air gaps is 0. 1 mm long. The number of turns of the coil (N) is 240. Assuming that the reluctance of the keeper is negligible, calculate the maximum mass in kg, which can be lifted by the system if a current of 1. 5 A is passed through the coil. You may neglect the fringing effect and flux leakage; and assume that

Calculation of maximum weight lifted by and electromagnet. Let the flux density in the air gap be For the air gap For the iron yoke

Total mmf; Since there are two air gaps;

Hysteresis loss Materials before applying m. m. f (H), the polarity of the molecules or structures are in random. After applying m. m. f (H) , the polarity of the molecules or structures are in one direction, thus the materials become magnetized. The more H applied the more magnetic flux (B )will be produced

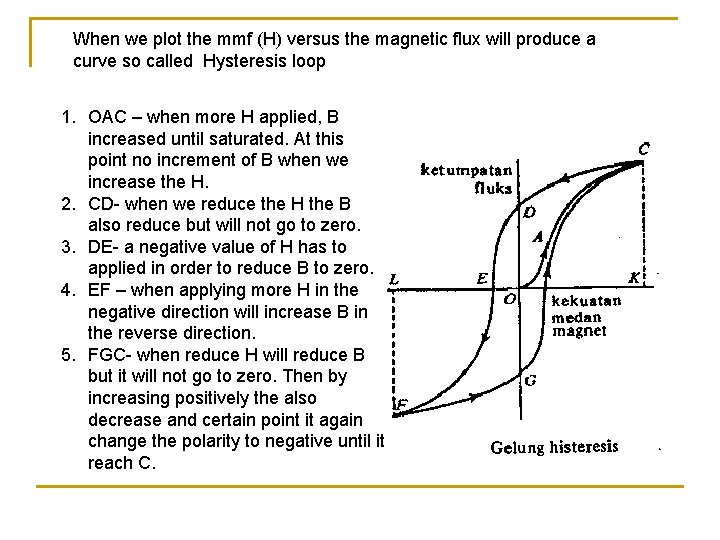
When we plot the mmf (H) versus the magnetic flux will produce a curve so called Hysteresis loop 1. OAC – when more H applied, B increased until saturated. At this point no increment of B when we increase the H. 2. CD- when we reduce the H the B also reduce but will not go to zero. 3. DE- a negative value of H has to applied in order to reduce B to zero. 4. EF – when applying more H in the negative direction will increase B in the reverse direction. 5. FGC- when reduce H will reduce B but it will not go to zero. Then by increasing positively the also decrease and certain point it again change the polarity to negative until it reach C.

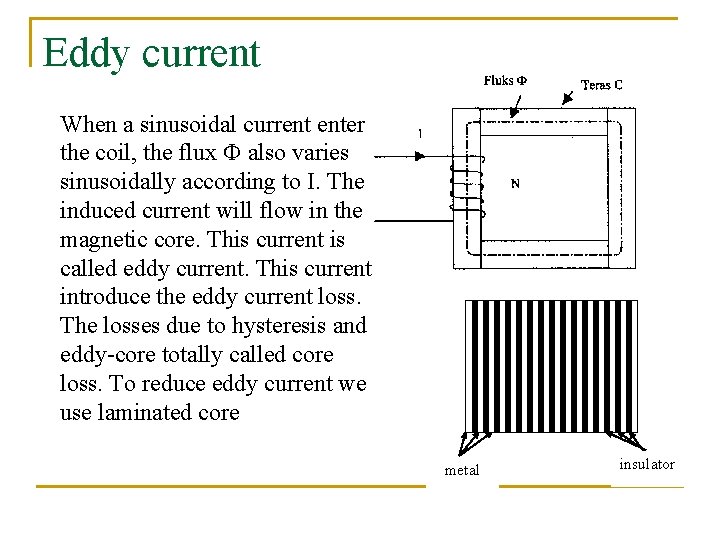
Eddy current When a sinusoidal current enter the coil, the flux also varies sinusoidally according to I. The induced current will flow in the magnetic core. This current is called eddy current. This current introduce the eddy current loss. The losses due to hysteresis and eddy-core totally called core loss. To reduce eddy current we use laminated core metal insulator