Todays agenda Magnetic Fields You must understand the

Today’s agenda: Magnetic Fields. You must understand the similarities and differences between electric fields and field lines, and magnetic fields and field lines. Magnetic Force on Moving Charged Particles. You must be able to calculate the magnetic force on moving charged particles. Magnetic Flux and Gauss’ Law for Magnetism. You must be able to calculate magnetic flux and recognize the consequences of Gauss’ Law for Magnetism. Motion of a Charged Particle in a Uniform Magnetic Field. You must be able to calculate the trajectory and energy of a charged particle moving in a uniform magnetic field.

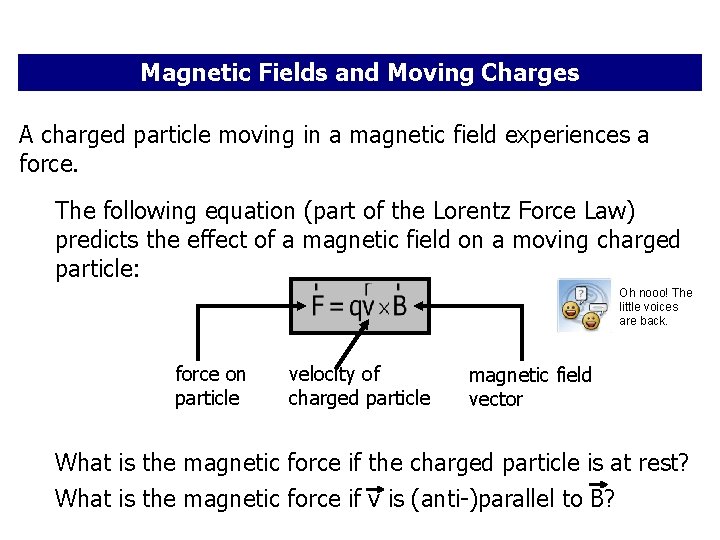
Magnetic Fields and Moving Charges A charged particle moving in a magnetic field experiences a force. The following equation (part of the Lorentz Force Law) predicts the effect of a magnetic field on a moving charged particle: Oh nooo! The little voices are back. force on particle velocity of charged particle magnetic field vector What is the magnetic force if the charged particle is at rest? What is the magnetic force if v is (anti-)parallel to B?

Vector notation conventions: is a vector pointing out of the paper/board/screen (looks like an arrow coming straight for your eye). is a vector pointing into the paper/board/screen (looks like the feathers of an arrow going away from eye).

Re Use right hand rule: a d fingers out in direction of v, thumb perpendicular to them w in ay untilgyour palm points in the direction of B rotate your hand i (or bend fingers through angle from v to B) to ssmallest n leof F ono+tcharge thumb points in direction ar a Your text presents two alternativen variations g (curl your fingers, th. There isoone imagine turning a right-handed screw). other o variation on the right hand rule. I’ll demonstrate all variations in i d s! lecture sooner or later. Direction of magnetic force--- still more variations: http: //hyperphysics. phy-astr. gsu. edu/hbase/magnetic/magfor. html

Complication: your Physics 1135 text uses the right hand rule shown in the figure, so we’ll use the same rule in Physics 2135. There a number of variations of this rule. Unfortunately, most of the Youtube videos I find say to use your palm for , your thumb for , and your outstretched fingers for This includes the MIT Open Courseware site. I’ll show you later that both ways are correct. I am going to use our textbook’s technique. You can use whatever works for you!

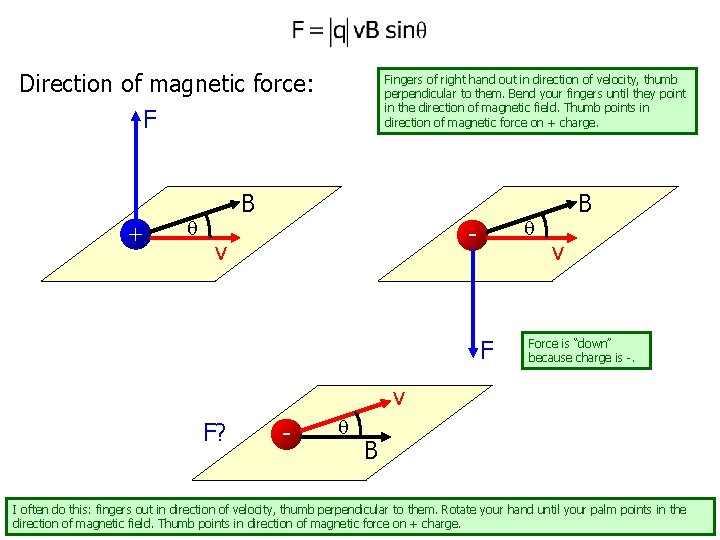
Direction of magnetic force: F + Fingers of right hand out in direction of velocity, thumb perpendicular to them. Bend your fingers until they point in the direction of magnetic field. Thumb points in direction of magnetic force on + charge. B - v F B v Force is “down” because charge is -. v F? - B I often do this: fingers out in direction of velocity, thumb perpendicular to them. Rotate your hand until your palm points in the direction of magnetic field. Thumb points in direction of magnetic force on + charge.

“Foolproof” technique for calculating both magnitude and direction of magnetic force. http: //www. youtube. com/watch? v=21 LWu. Y 8 i 6 Hw All of the right-hand rules are just techniques for determining the direction of vectors in the cross product without having to do any actual math.

^ Example: a proton is moving with a velocity v = v 0 j in a region ^ of uniform magnetic field. The resulting force is F = F 0 i. What is the magnetic field (magnitude and direction)? To be worked at the blackboard. Blue is +, red is -. Image from http: //www. mathsisfun. com/algebra/matrix-determinant. htm

^ Example: a proton is moving with a velocity v = v 0 j in a region ^ of uniform magnetic field. The resulting force is F = F 0 i. What is the magnetic field (magnitude and direction)?

^ Example: a proton is moving with a velocity v = v 0 j in a region ^ of uniform magnetic field. The resulting force is F = F 0 i. What is the magnetic field (magnitude and direction)? What is By? ? It could be anything. Not enough information is provided to find By. We can’t find the magnitude and direction of the magnetic field using only the information given!

^ Example: a proton is moving with a velocity v = v 0 j in a region ^ of uniform magnetic field. The resulting force is F = F 0 i. What is the minimum magnitude magnetic field that can be present? for a minimum magnitude magnetic field, so. . .

Homework Hint A charged particle moving along or opposite to the direction of a magnetic field will experience no magnetic force. Conversely, the fact that there is no magnetic force along some direction does not mean there is no magnetic field along or opposite to that direction. It’s OK to use if you know that v and B are perpendicular, or you are calculating a minimum field to produce a given force (understand why).

Alternative* view of magnetic field units. Remember, units of field are force per “something. ” *“Official” definition of units coming later.