Magnetic Force Strength of Magnetic Force A charged

Magnetic Force

Strength of Magnetic Force A charged particle moving in a magnetic field experiences a force that is perpendicular to BOTH the particle’s velocity and to the magnetic field itself.

Strength of Magnetic Force A charged particle moving in a magnetic field experiences a force that is perpendicular to BOTH the particle’s velocity and to the magnetic field itself. Lorentz Force Law: The magnitude of the magnetic force on a moving, charged particle is F = qv. B sin q (q is the angle between the charge’s velocity and the magnetic field)

F = qv. B sin q Sin 0, 180 = 0 If a charge has velocity in the same (or opposite) direction of the magnetic field, it experiences no force! Sin 90 = 1 A charge that has velocity perpendicular to the magnetic field experiences the greatest force!

Question? The three charges below have equal charge and speed, but are traveling in different directions in a uniform magnetic field. Which particle experiences the greatest magnetic force? 1 2 3 3 2 1 Same B F = q v B sin q

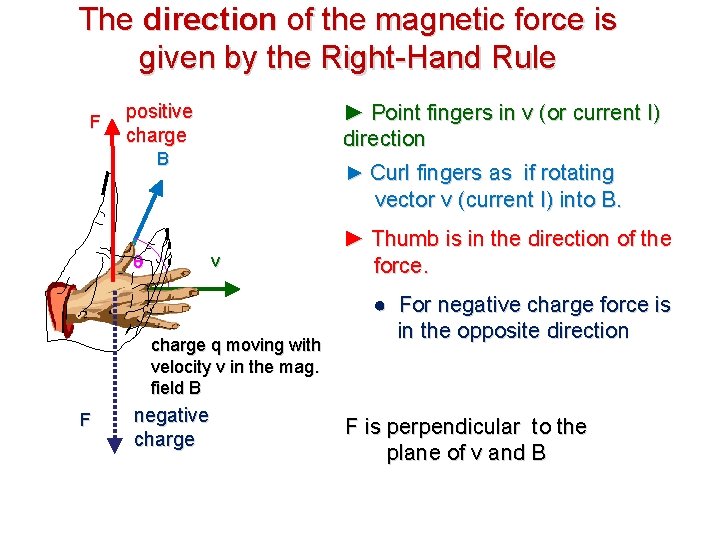
The direction of the magnetic force is given by the Right-Hand Rule F positive charge ► Point fingers in v (or current I) direction B ► Curl fingers as if rotating vector v (current I) into B. q v charge q moving with velocity v in the mag. field B F negative charge ► Thumb is in the direction of the force. ● For negative charge force is in the opposite direction F is perpendicular to the plane of v and B

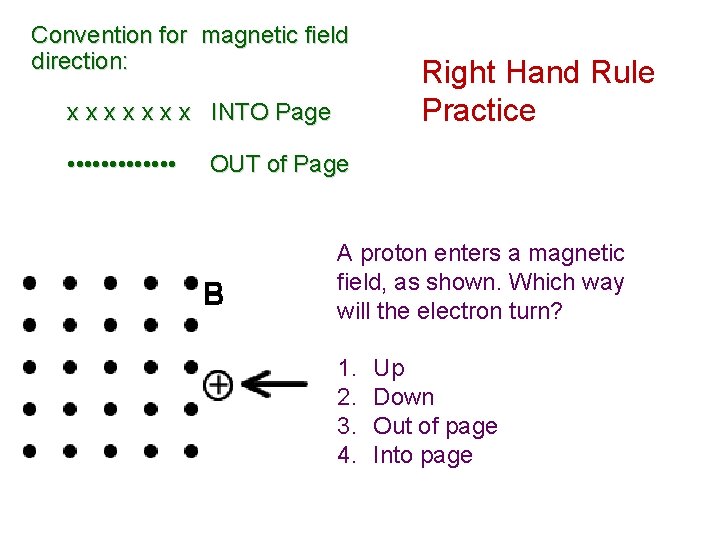
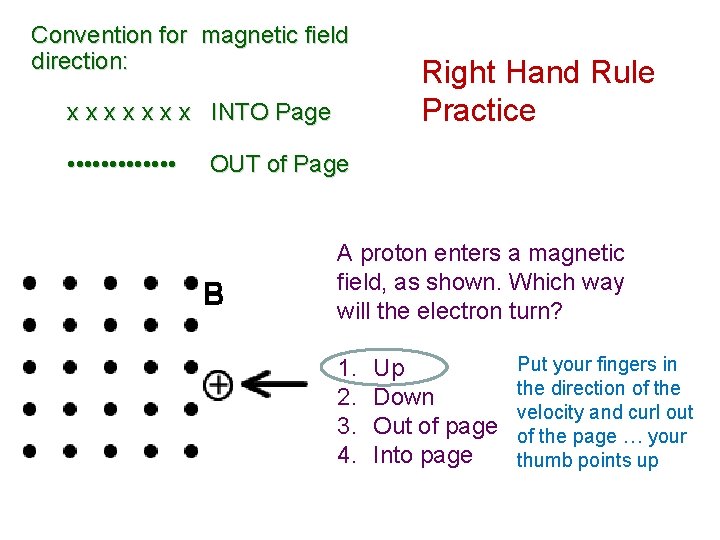
Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page A proton enters a magnetic field, as shown. Which way will the electron turn? 1. 2. 3. 4. Up Down Out of page Into page

Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page A proton enters a magnetic field, as shown. Which way will the electron turn? 1. 2. 3. 4. Up Down Out of page Into page Put your fingers in the direction of the velocity and curl out of the page … your thumb points up

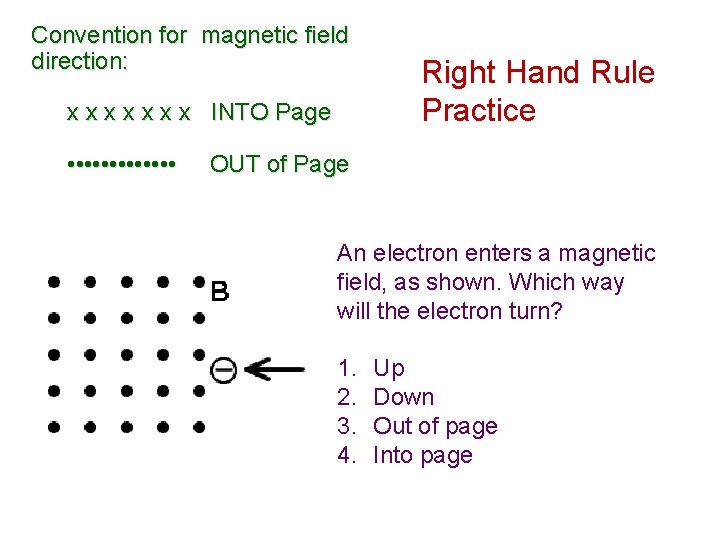
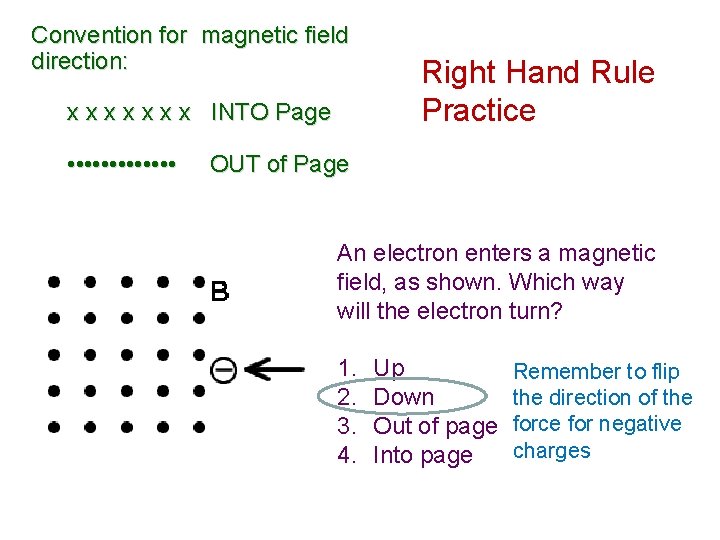
Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page An electron enters a magnetic field, as shown. Which way will the electron turn? 1. 2. 3. 4. Up Down Out of page Into page

Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page An electron enters a magnetic field, as shown. Which way will the electron turn? 1. 2. 3. 4. Up Down Out of page Into page Remember to flip the direction of the force for negative charges

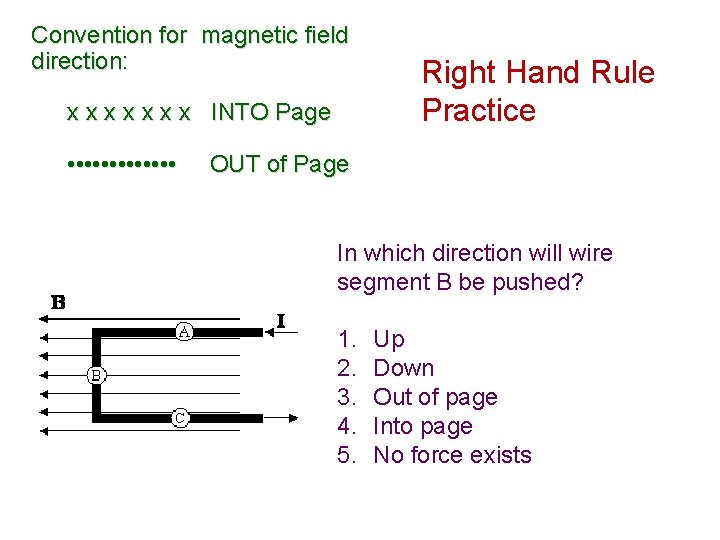
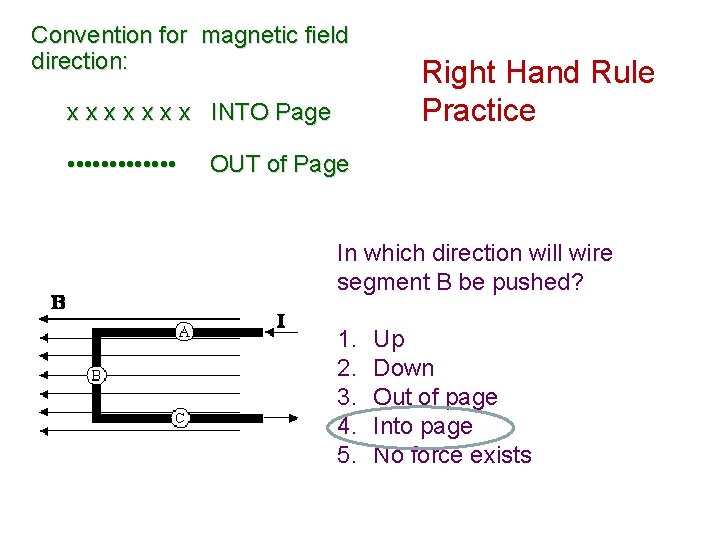
Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page In which direction will wire segment B be pushed? 1. 2. 3. 4. 5. Up Down Out of page Into page No force exists

Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page In which direction will wire segment B be pushed? 1. 2. 3. 4. 5. Up Down Out of page Into page No force exists

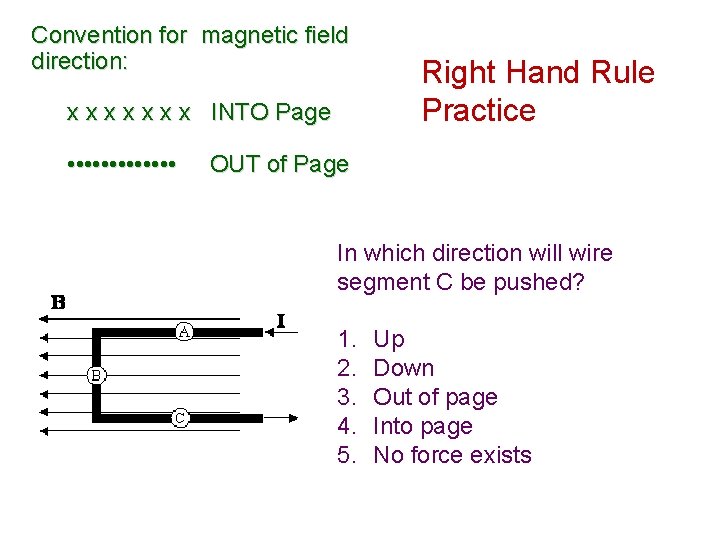
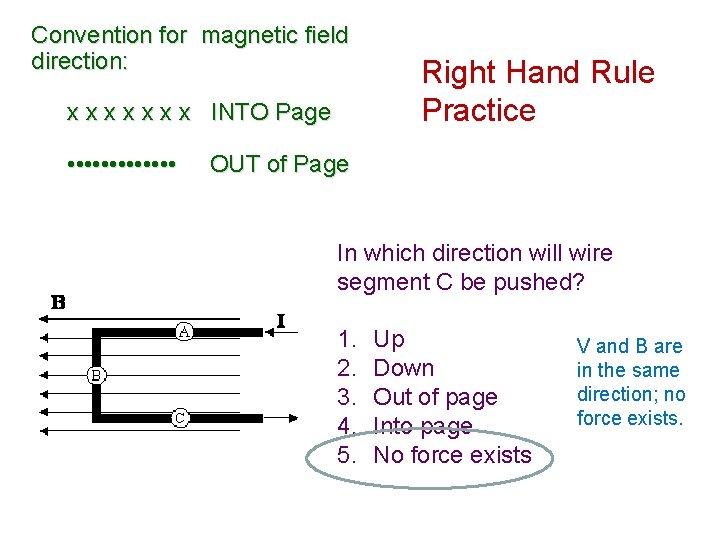
Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page In which direction will wire segment C be pushed? 1. 2. 3. 4. 5. Up Down Out of page Into page No force exists

Convention for magnetic field direction: x x x x INTO Page • • • • Right Hand Rule Practice OUT of Page In which direction will wire segment C be pushed? 1. 2. 3. 4. 5. Up Down Out of page Into page No force exists V and B are in the same direction; no force exists.

Magnitude of the magnetic field We define the magnitude of the magnetic field by measuring the force on a moving charge : B q v The SI unit of magnetic field is the Tesla (T), named after Nikola Tesla, a Croatian physicist. 1 T = 1 N·s/(C·m)

Magnetic Field & Magnetic Force Problems We do: What is the minimum magnetic field necessary to exert a 5. 4 X 10 -15 N force on an electron moving at 2. 1 X 107 m/s?

Magnetic Field & Magnetic Force Problems We do: What is the minimum magnetic field necessary to exert a 5. 4 X 10 -15 N force on an electron moving at 2. 1 X 107 m/s? B = F / qvsinθ B will be at a minimum when sin θ = 1 B = F / qv = 5. 4 X 10 -15 N / (1. 6 X 10 -19 C X 2. 1 X 107 m/s) B = 1. 61 X 10 -3 T

Magnetic Field & Magnetic Force Problems You do: What is the magnetic field necessary to exert a 5. 4 X 10 -15 N force on an electron moving at 2. 1 X 107 m/s if the magnetic field is at 45 degrees from the electron’s velocity?

Magnetic Field & Magnetic Force Problems You do: What is the magnetic field necessary to exert a 5. 4 X 10 -15 N force on an electron moving at 2. 1 X 107 m/s if the magnetic field is at 45 degrees from the electron’s velocity? B = F / qvsinθ = 5. 4 X 10 -15 N / (1. 6 X 10 -19 C X 2. 1 X 107 m/s X sin 45) B = 2. 3 X 10 -3 T.

Magnetic Field & Magnetic Force Problems We do and You do What is the magnitude of the magnetic force on a proton moving at 2. 5 X 105 m/s in a magnetic field of 0. 5 T … (a) …if the velocity and magnetic field are at right angles? (b) … if the velocity and magnetic field are at 30°? (c) … if the velocity is parallel to a magnetic field?

Magnetic Field & Magnetic Force Problems We do and You do What is the magnitude of the magnetic force on a proton moving at 2. 5 X 105 m/s in a magnetic field of 0. 5 T … (a) …if the velocity and magnetic field are at right angles? (b) … if the velocity and magnetic field are at 30°? (c) … if the velocity is parallel to a magnetic field? F = qv. Bsinθ , so (a) when θ = 90°, F = (1. 6 X 10 -19 C)(2. 5 X 105 m/s)(0. 5 T) = 2. 0 X 10 -14 N, (b) F = (2. 0 X 10 -14 N) sin 30° = 1. 0 X 10 -14 N, and (c) F = qv. B sin 0° = 0.

Comparison of Electric and Magnetic Forces Using your notes, and working in small groups (3 or less), compare the electric and magnetic forces in terms of: • • Magnitude Direction Work done Effect on charged particles

Comparison of Electric and Magnetic Forces The electric force: Felec = Eq q is always parallel to the direction of the electric field. q acts on a charged particle independent of the particle’s velocity The magnetic force: Fmag = qv. B sin q q is always perpendicular to the direction of the magnetic field q acts on a charged particle only when the particle is in motion (F=0 if v=0), and only q does work when moving if v and B do not point in the same or charge: opposite direction (sin 00 = sin 1800 = 0). The work, W = Fel d cosθ 1, is q Force is perpendicular to motion so the In the presence of magnetic field, the converted into kinetic / thermal work moving charged particle is deflected energy. done by magnetic force is zero. (dotted lines) W = Fmagd cosq 1 = 0 (cos 900 = 0). The electric field accelerates Change in kinetic energy of the