Electricity Magnetism Review of Coulombs Force Magnetic Fields

Electricity&… Magnetism Review of Coulomb`s Force, Magnetic Fields and Magnetic Force Lecture 22 Monday: 5 April 2004

Coulomb’s Law

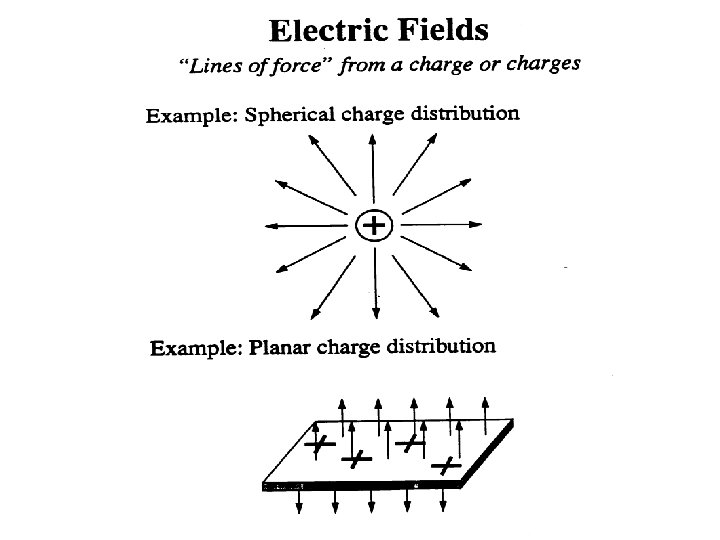
Electromagnetism · fundamental force · Interplay between electricity and magnetism · Produces electromagnetic waves (“light”) Electricity · Electric fields · Set up by electric charges F = q. E Magnetism · Magnetic fields · Set up by electric currents (moving charges) Fmag= qv x B, v parallel to B then Fmag = 0 F = Fel + Fmag = q. E + qv x B

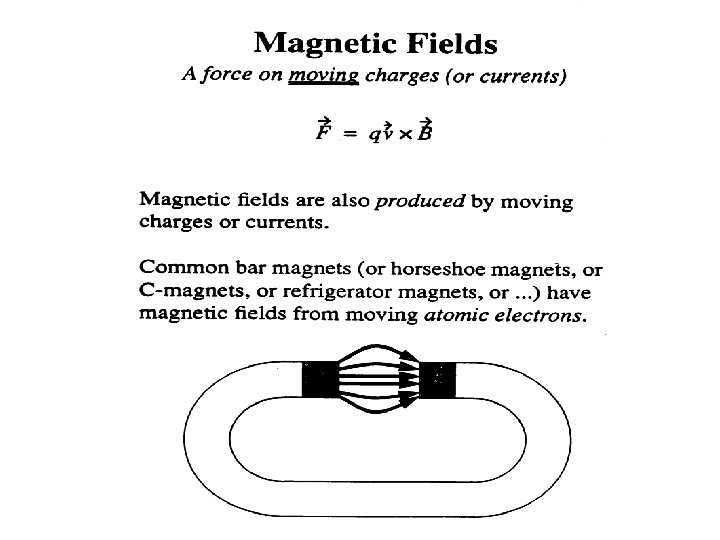
Interaction Forces Between Magnets • Like poles repel, and unlike poles attract. • Poles cannot be isolated. They occur only in pairs, as dipoles.

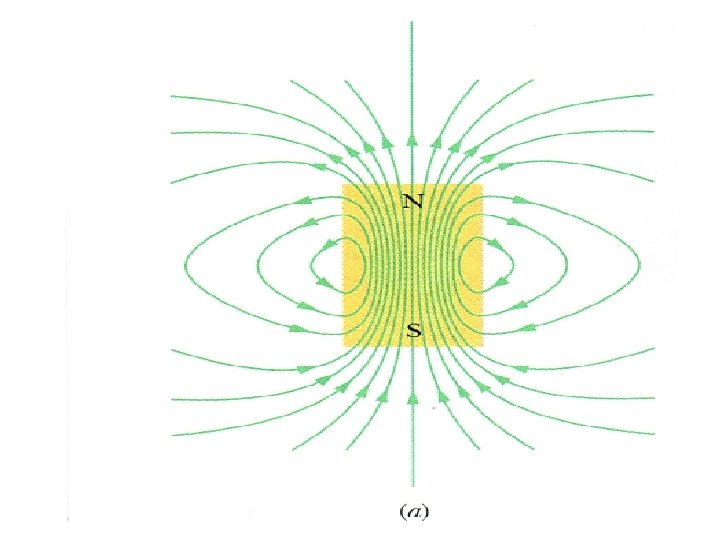
Magnetic Fields • Just as we found defining an electric field useful, we will find defining a magnetic field useful. • B is the symbol for the magnetic field. • Magnetic field lines run from north poles to south poles.

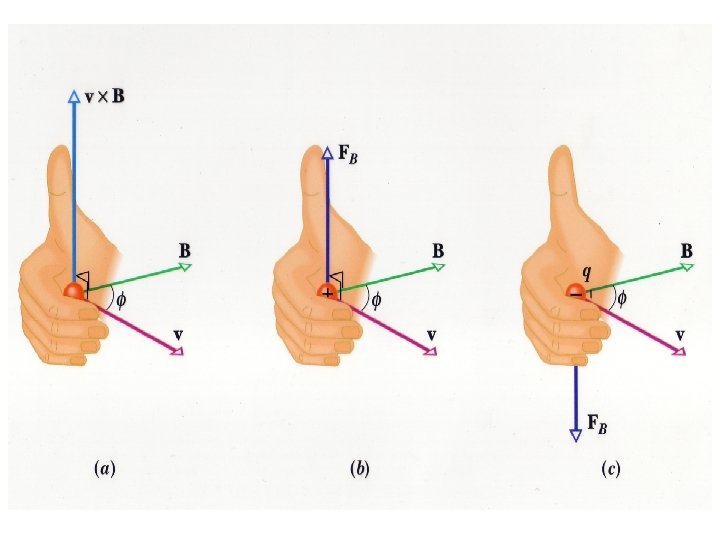
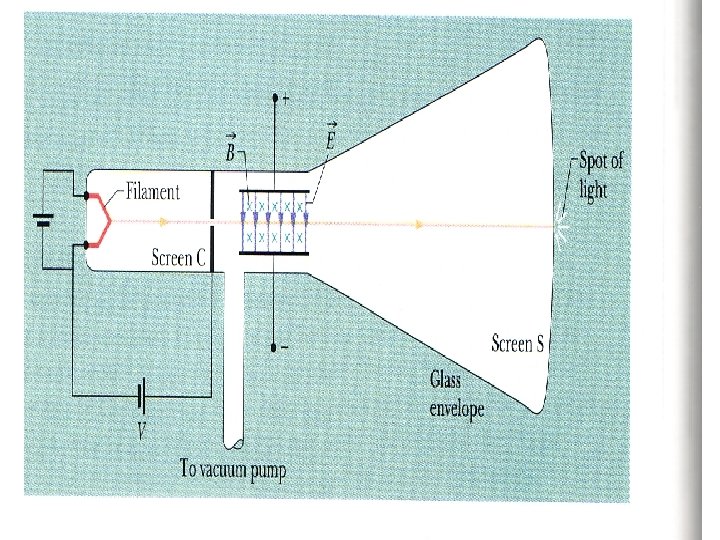
Charges in a Magnetic Field • Moving charges experience a force due to a magnetic field. FB = qv × B • Magnitude of FB is: FB = qv. B sin f • where f is the angle between v and B. • Direction is from the right hand rule.

Another Example

THE MAGNETIC FIELD • B is the symbol for the magnetic field. • Magnetic field lines run from north poles to south poles.

Charges in a Magnetic Field • The magnetic force on a moving charge is perpendicular to the direction of the magnetic field, and perpendicular to the direction of the velocity of the charge. • If a charge moves parallel to the direction of a magnetic field, it experiences no magnetic force.

A charged particle enters a uniform magnetic field perpendicular to the field… • Speed doesn’t change since acceleration is always perpendicular to the direction of motion. • Motion stays perpendicular to the field

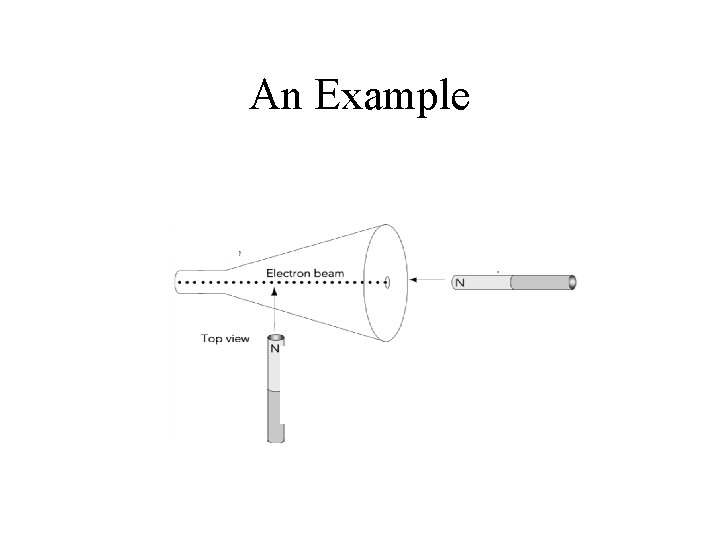
An Example

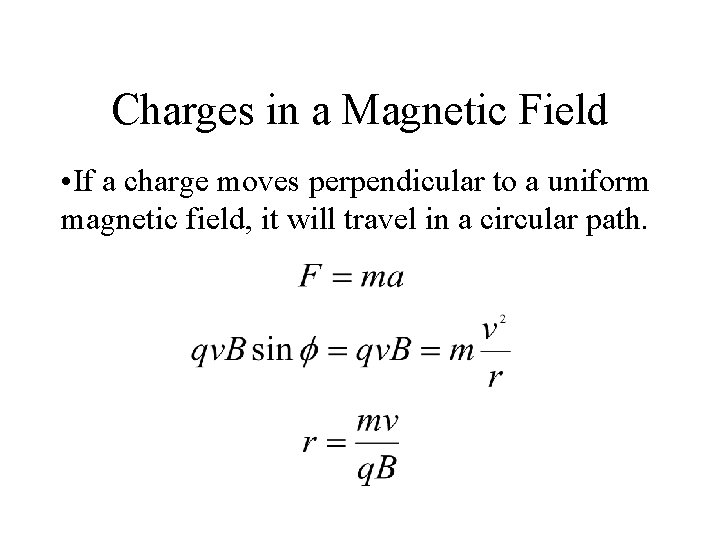
Charges in a Magnetic Field • If a charge moves perpendicular to a uniform magnetic field, it will travel in a circular path.

Application • Earth’s magnetic field shields us from incoming charged particles. However, since Earth’s magnetic field goes from the south pole to the north, particles can travel parallel to the field and enter the atmosphere near the poles. The “aurora” is the result.

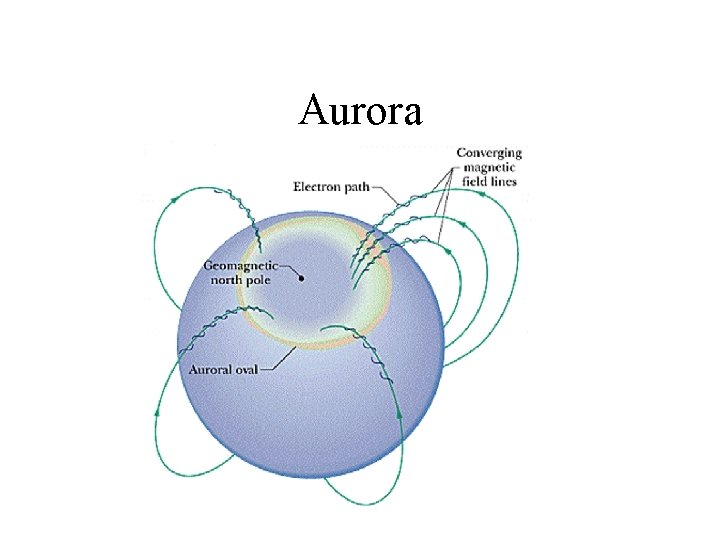
Aurora

Mass Spectrometer • The radius of the orbit of a charged particle depends on its mass. If we know its charge and speed, we can determine its mass from the radius of the orbit.

Mass Spectrometer

Mass Spectrometer • However, if v is not known, the system can still work, in terms of the accelerating potential V.

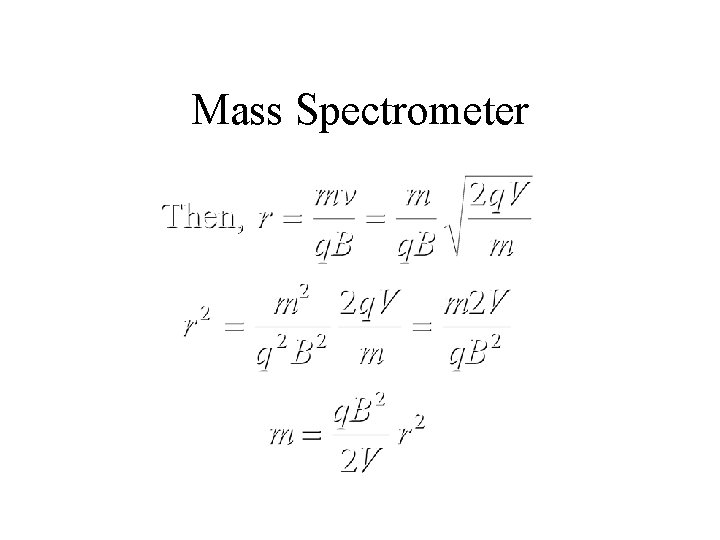
Mass Spectrometer

Frequency and Period

Angular Frequency • Frequency or period of a circular orbit in a magnetic field does not depend on radius.

Charges in a Magnetic Field • Moving charges experience a force due to a magnetic field. FB = qv × B • Magnitude of FB is: FB = qv. B sin f • where f is the angle between v and B. • Direction is from the right hand rule.

An Example