Chapter 28 Magnetic Force Fields 2 Applications Charged

Chapter 28 Magnetic Force & Fields (2)

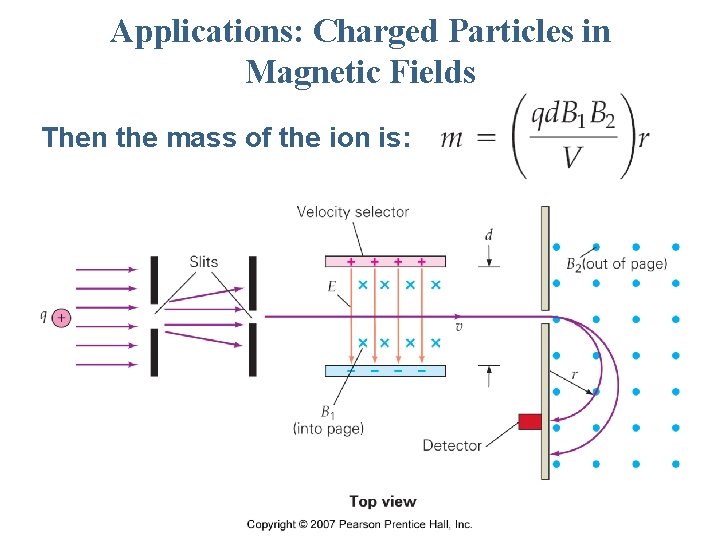
Applications: Charged Particles in Magnetic Fields A velocity selector consists of an electric and magnetic field at right angles to each other. Ions entering the selector will experience an electric force: and a magnetic force: These two forces will be opposite to each other.

Applications: Charged Particles in Magnetic Fields Given the values of the electric and magnetic fields, there will be a single velocity that will allow ions to pass through the selector undeflected. 1 1 But E = V/d, therefore:

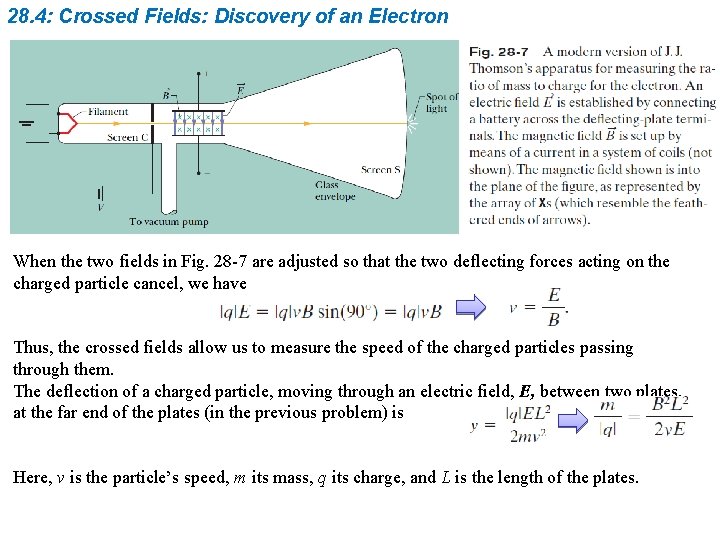
28. 4: Crossed Fields: Discovery of an Electron When the two fields in Fig. 28 -7 are adjusted so that the two deflecting forces acting on the charged particle cancel, we have Thus, the crossed fields allow us to measure the speed of the charged particles passing through them. The deflection of a charged particle, moving through an electric field, E, between two plates, at the far end of the plates (in the previous problem) is Here, v is the particle’s speed, m its mass, q its charge, and L is the length of the plates.

28. 4. 1. An electron is traveling due south in a region of space at a constant speed. What can you conclude from this situation regarding the presence any electric and/or magnetic fields? a) The electric field must be zero, but the magnetic field might be non-zero in the region. b) The magnetic field must be zero, but the electric field might be non-zero in the region. c) Both the electric and magnetic field might be non-zero, but they are perpendicular to each other in the region. d) Both the electric and magnetic field might be non-zero, but they point in opposite directions in the region. e) Both the electric and magnetic field must be zero in the region.

28. 4. 1. An electron is traveling due south in a region of space at a constant speed. What can you conclude from this situation regarding the presence any electric and/or magnetic fields? a) The electric field must be zero, but the magnetic field might be non-zero in the region. b) The magnetic field must be zero, but the electric field might be non-zero in the region. c) Both the electric and magnetic field might be non-zero, but they are perpendicular to each other in the region. d) Both the electric and magnetic field might be non-zero, but they point in opposite directions in the region. e) Both the electric and magnetic field must be zero in the region.

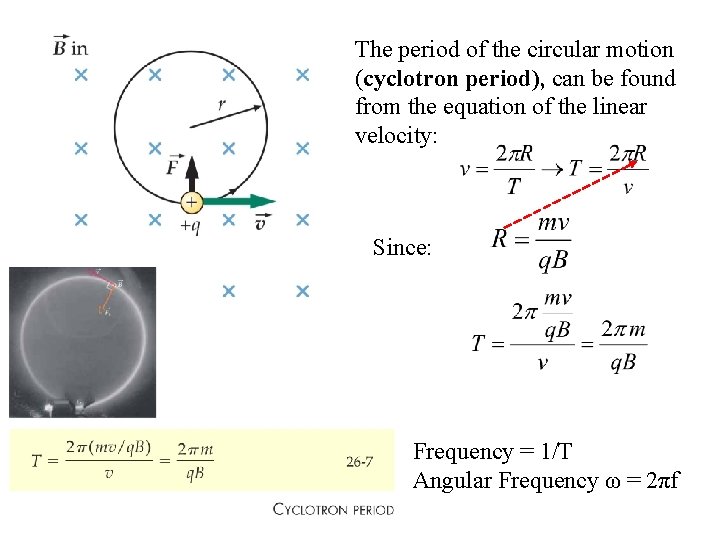
The period of the circular motion (cyclotron period), can be found from the equation of the linear velocity: Since: Frequency = 1/T Angular Frequency ω = 2πf

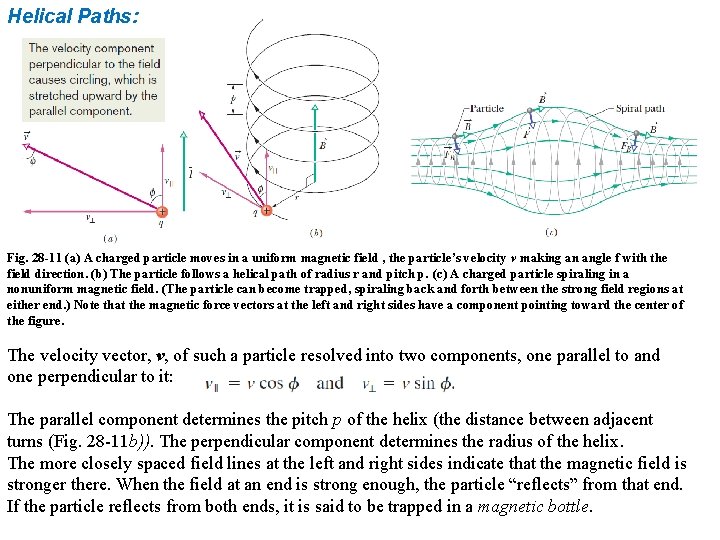
Helical Paths: Fig. 28 -11 (a) A charged particle moves in a uniform magnetic field , the particle’s velocity v making an angle f with the field direction. (b) The particle follows a helical path of radius r and pitch p. (c) A charged particle spiraling in a nonuniform magnetic field. (The particle can become trapped, spiraling back and forth between the strong field regions at either end. ) Note that the magnetic force vectors at the left and right sides have a component pointing toward the center of the figure. The velocity vector, v, of such a particle resolved into two components, one parallel to and one perpendicular to it: The parallel component determines the pitch p of the helix (the distance between adjacent turns (Fig. 28 -11 b)). The perpendicular component determines the radius of the helix. The more closely spaced field lines at the left and right sides indicate that the magnetic field is stronger there. When the field at an end is strong enough, the particle “reflects” from that end. If the particle reflects from both ends, it is said to be trapped in a magnetic bottle.

Example, Helical Motion of a Charged Particle in a Magnetic Field:

Applications: Charged Particles in Magnetic Fields Then the mass of the ion is:

Example, Uniform Circular Motion of a Charged Particle in a Magnetic Field:

Cyclotrons and Synchrotrons Suppose that a proton, injected by source S at the center of the cyclotron in Fig. 28 -13, initially moves toward a negatively charged dee. It will accelerate toward this dee and enter it. Once inside, it is shielded from electric fields by the copper walls of the dee; that is, the electric field does not enter the dee. The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in a circular path whose radius, which depends on its speed, is given by (r =mv/|q|B). Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed. Thus, the proton again faces a negatively charged dee and is again accelerated. This process continues, the circulating proton always being in step with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system. There a deflector plate sends it out through a portal. The frequency f at which the proton circulates in the magnetic field (and that does not depend on its speed) must be equal to the fixed frequency fosc of the electrical oscillator:

The Proton Synchrotron : At proton energies above 50 Me. V, the conventional cyclotron begins to fail. Also, for a 500 Ge. V proton in a magnetic field of 1. 5 T, the path radius is 1. 1 km. The corresponding magnet for a conventional cyclotron of the proper size would be impossibly expensive. In the proton synchrotron the magnetic field B, and the oscillator frequency fosc, instead of having fixed values as in the conventional cyclotron, are made to vary with time during the accelerating cycle. When this is done properly, (1) the frequency of the circulating protons remains in step with the oscillator at all times, and (2) the protons follow a circular—not a spiral—path. Thus, the magnet need extend only along that circular path, not over some 4 x 106 m 2. The circular path, however, still must be large if high energies are to be achieved. The proton synchrotron at the Fermi National Accelerator Laboratory (Fermilab) in Illinois has a circumference of 6. 3 km and can produce protons with energies of about 1 Te. V ( 1012 e. V).

Example, Accelerating a Charged Particle in a Synchrotron:

28. 7. 1. Ernest O. Lawrence, of the University of California, Berkeley, invented the cyclotron in 1929. A more modern version was completed in 1961 at the Lawrence-Livermore Laboratory that has a radius of 88 inches. What is the frequency of circular motion at the “ 88 -incher” if protons are circulating in a magnetic field of 0. 48 T? a) 1. 4 × 106 Hz b) 4. 5 × 106 Hz c) 7. 3 × 106 Hz d) 3. 6 × 105 Hz e) 9. 7 × 104 Hz

28. 7. 1. Ernest O. Lawrence, of the University of California, Berkeley, invented the cyclotron in 1929. A more modern version was completed in 1961 at the Lawrence-Livermore Laboratory that has a radius of 88 inches. What is the frequency of circular motion at the “ 88 -incher” if protons are circulating in a magnetic field of 0. 48 T? a) 1. 4 × 106 Hz b) 4. 5 × 106 Hz c) 7. 3 × 106 Hz d) 3. 6 × 105 Hz e) 9. 7 × 104 Hz

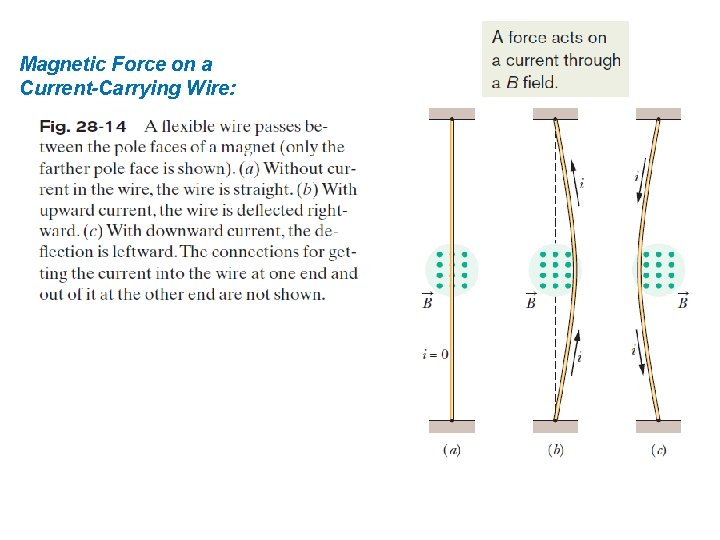
Magnetic Force on a Current-Carrying Wire:

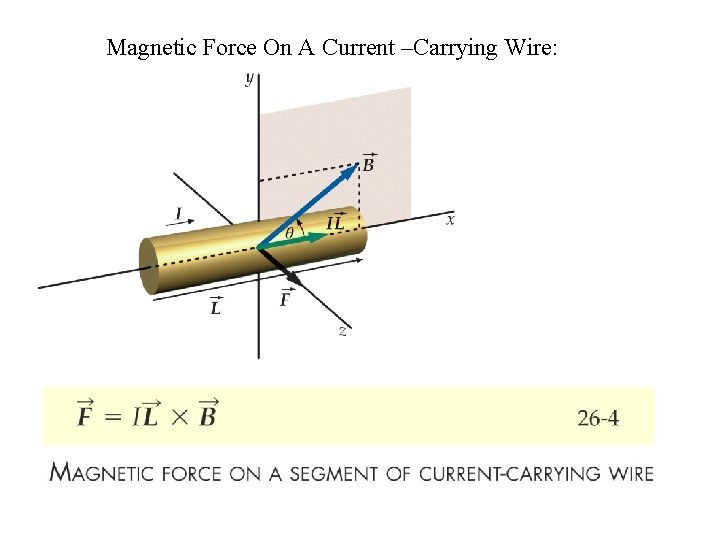
Magnetic Force on a Current-Carrying Wire: Consider a length L of the wire in the figure. All the conduction electrons in this section of wire will drift past plane xx in a time t =L/vd. Thus, in that time a charge will pass through that plane that is given by Here L is a length vector that has magnitude L and is directed along the wire segment in the direction of the (conventional) current. If a wire is not straight or the field is not uniform, we can imagine the wire broken up into small straight segments. The force on the wire as a whole is then the vector sum of all the forces on the segments that make it up. In the differential limit, we can write and we can find the resultant force on any given arrangement of currents by integrating Eq. 28 -28 over that arrangement.

Example, Magnetic Force on a Wire Carrying Current:

Magnetic Force on a Current • Consider a current-carrying wire in the N presence of a magnetic field B. • There will be a force on each of the charges moving in the wire. What will be the total force d. F on a length dl of the wire? • Suppose current is made up of n charges/volume each carrying charge q and moving with velocity v through a wire of cross-section A. • Force on each charge = • Total force = • Current = Þ Simpler: For a straight length of wire L carrying a current I, the force on it is: S

Magnetic Force On A Current –Carrying Wire:

Magnetic Force on a Current Loop • Consider loop in magnetic field as on right: If field is ^ to plane of loop, the net force on loop is 0! x x Fx – Force on top path cancels force x on bottom path (F = IBL) x x x – Force on right path cancels force on left path. (F = IBL) • If plane of loop is not ^ to field, there will be a non-zero torque on the loop! F x x x x x. I F x x x B x x F x B x F F.

Square Loop A square loop of wire is carrying current in the counterclockwise direction. There is a horizontal uniform magnetic field pointing to the right. 2) What is the force on section a-b of the loop? a) zero b) out of the page c) into the page 3) What is the force on section b-c of the loop? a) zero b) out of the page c) into the page 4) What is the net force on the loop? a) zero b) out of the page c) into the page

ab: Fab = 0 = Fcd since the wire is parallel to B. bc: Fbc = ILB RHR: I is up, B is to the right, so F points into the screen. By symmetry:

28. 8. 1. Three long, straight, identical wires are inserted one at a time into a magnetic field directed due east. Wire A carries a current of 2 A in the direction of 45 south of east. Wire B carries a current of 8 A, due north. Wire C carries a current of 10 A, due west. Rank the wires in terms of the magnitude of the magnetic force on each wire, with the largest force listed first and the smallest force listed last. a) A > B > C b) B > A > C c) C > B > A d) A > C > B e) B > C > A

28. 8. 1. Three long, straight, identical wires are inserted one at a time into a magnetic field directed due east. Wire A carries a current of 2 A in the direction of 45 south of east. Wire B carries a current of 8 A, due north. Wire C carries a current of 10 A, due west. Rank the wires in terms of the magnitude of the magnetic force on each wire, with the largest force listed first and the smallest force listed last. a) A > B > C b) B > A > C c) C > B > A d) A > C > B e) B > C > A

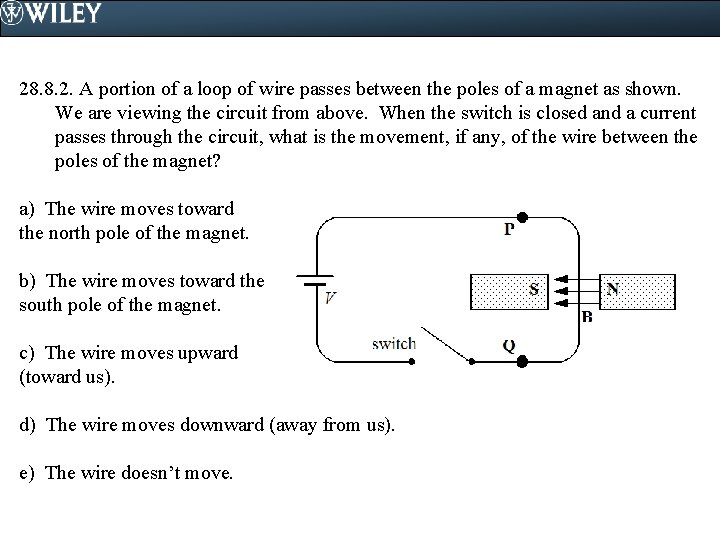
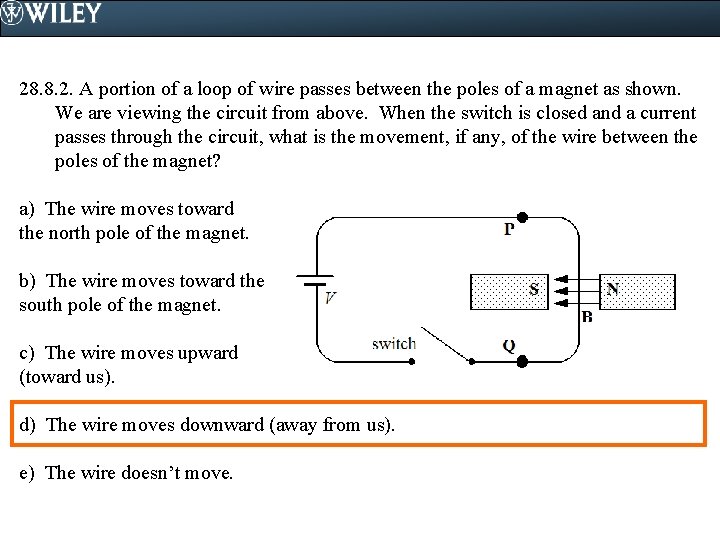
28. 8. 2. A portion of a loop of wire passes between the poles of a magnet as shown. We are viewing the circuit from above. When the switch is closed and a current passes through the circuit, what is the movement, if any, of the wire between the poles of the magnet? a) The wire moves toward the north pole of the magnet. b) The wire moves toward the south pole of the magnet. c) The wire moves upward (toward us). d) The wire moves downward (away from us). e) The wire doesn’t move.

28. 8. 2. A portion of a loop of wire passes between the poles of a magnet as shown. We are viewing the circuit from above. When the switch is closed and a current passes through the circuit, what is the movement, if any, of the wire between the poles of the magnet? a) The wire moves toward the north pole of the magnet. b) The wire moves toward the south pole of the magnet. c) The wire moves upward (toward us). d) The wire moves downward (away from us). e) The wire doesn’t move.

Magnetic Force • A current I flows in a wire which is formed in the shape of an isosceles right triangle as shown. A constant magnetic field exists in the -z direction. – What is Fy, net force on the wire in the y-direction? (a) Fy < 0 (b) Fy = 0 y B (c) Fy > 0 x x x x Lx x x x x x x

Magnetic Force • A current I flows in a wire which is formed in the shape of an isosceles right triangle as shown. A constant magnetic field exists in the -z direction. – What is Fy, net force on the wire in the y-direction? (a) Fy < 0 (b) Fy = 0 y B x x x x Lx x x (c) Fy > 0 • The forces on each segment are determined by: • From symmetry, Fx = 0 • For the y-component: 45˚ F 1 F 2 • Therefore: F 3 There is never a net force on a loop in a uniform field! x x x Lx x x x

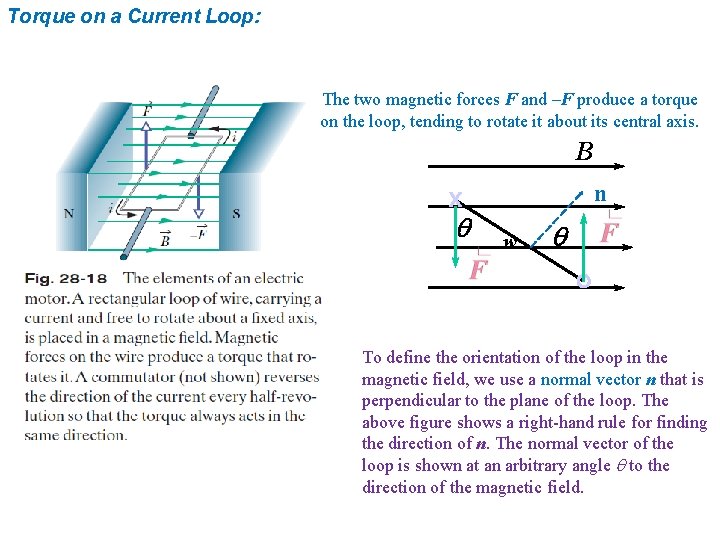
Torque on a Current Loop: The two magnetic forces F and –F produce a torque on the loop, tending to rotate it about its central axis. B n x q w q. To define the orientation of the loop in the magnetic field, we use a normal vector n that is perpendicular to the plane of the loop. The above figure shows a right-hand rule for finding the direction of n. The normal vector of the loop is shown at an arbitrary angle q to the direction of the magnetic field.

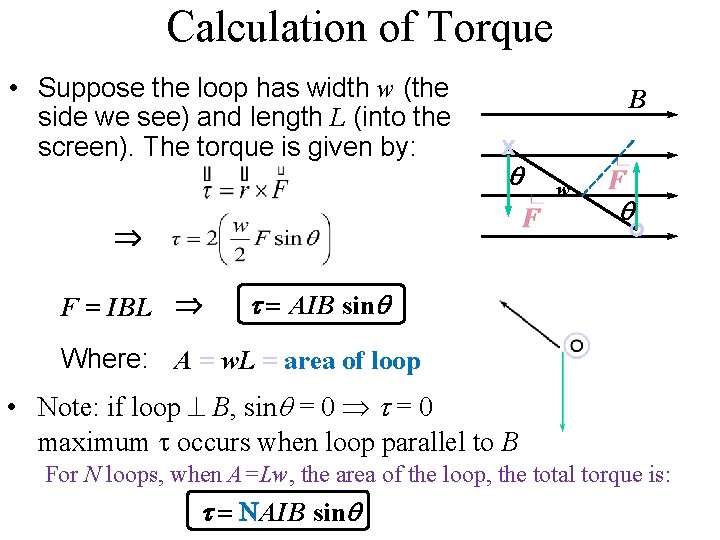
Calculation of Torque • Suppose the loop has width w (the side we see) and length L (into the screen). The torque is given by: B x q Þ F = IBL Þ w q. t = AIB sinq Where: A = w. L = area of loop • Note: if loop ^ B, sinq = 0 t = 0 maximum t occurs when loop parallel to B For N loops, when A=Lw, the area of the loop, the total torque is: t = NAIB sinq

Figure 28 -45 shows a wood cylinder of mass m = 0. 250 kg and length L = 0. 100 m, with N = 10. 0 turns of wire wrapped around it longitudinally, so that the plane of the wire coil contains the long central axis of the cylinder. The cylinder is released on a plane inclined at an angle θ to the horizontal, with the plane of the coil parallel to the incline plane. If there is a vertical uniform magnetic field of magnitude 0. 500 T, what is the least current i through the coil that keeps the cylinder from rolling down the plane t = NAi. B sinq f = mgsinθ fr = N 2 r. Li. Bsinq

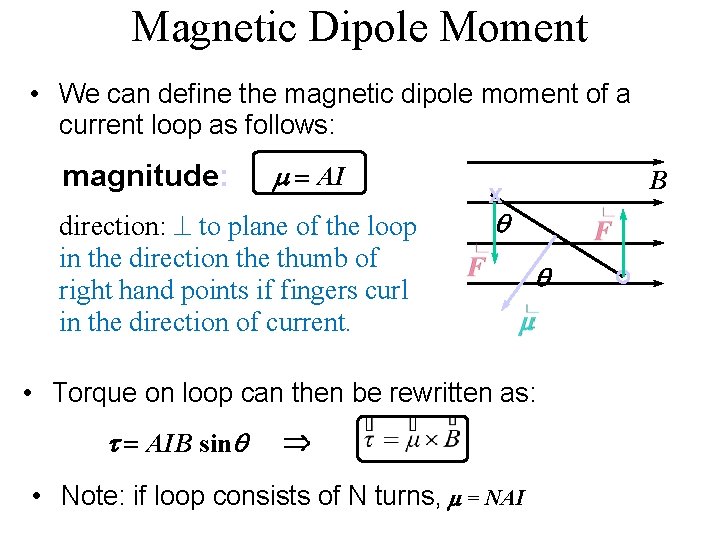
Magnetic Dipole Moment • We can define the magnetic dipole moment of a current loop as follows: magnitude: m = AI direction: ^ to plane of the loop in the direction the thumb of right hand points if fingers curl in the direction of current. B x q q • Torque on loop can then be rewritten as: t = AIB sinq Þ • Note: if loop consists of N turns, m = NAI .

The Magnetic Dipole Moment, m: From the above equations, one can see thatthe unit of m can be the joule per tesla (J/T), or the ampere–square meter.

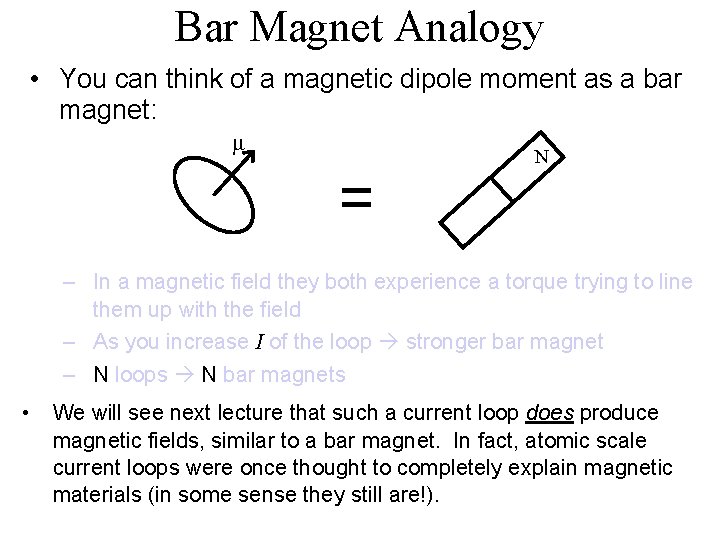
Bar Magnet Analogy • You can think of a magnetic dipole moment as a bar magnet: μ = N – In a magnetic field they both experience a torque trying to line them up with the field – As you increase I of the loop stronger bar magnet – N loops N bar magnets • We will see next lecture that such a current loop does produce magnetic fields, similar to a bar magnet. In fact, atomic scale current loops were once thought to completely explain magnetic materials (in some sense they still are!).

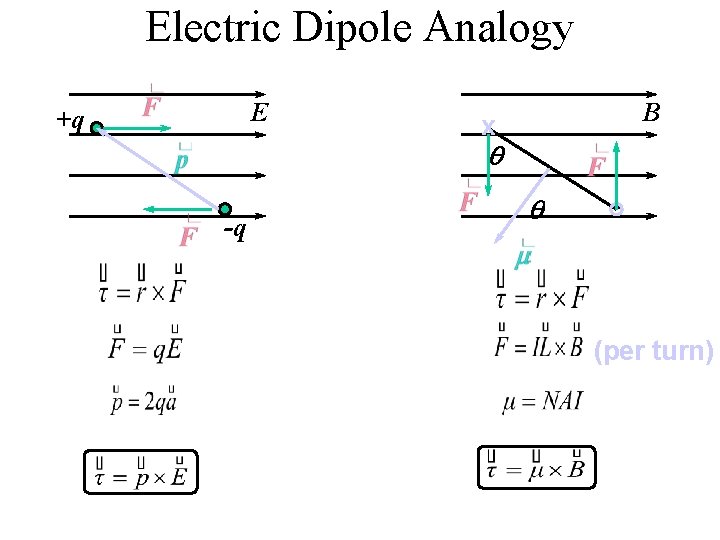
Electric Dipole Analogy E +q B x q . -q q . (per turn)

Square Loop A square loop of wire is carrying current in the counterclockwise direction. There is a horizontal uniform magnetic field pointing to the right. What is the net torque on the loop? a) zero b) up c) down d) out of the page e) into the page

The torque due to Fcb is up, since r (from the center of the loop) is to the right, and Fcb is into the page. Same goes for Fda. m points out of the page (curl your fingers in the direction of the current around the loop, and your thumb gives the direction of m). Use the RHR to find the direction of t to be up.

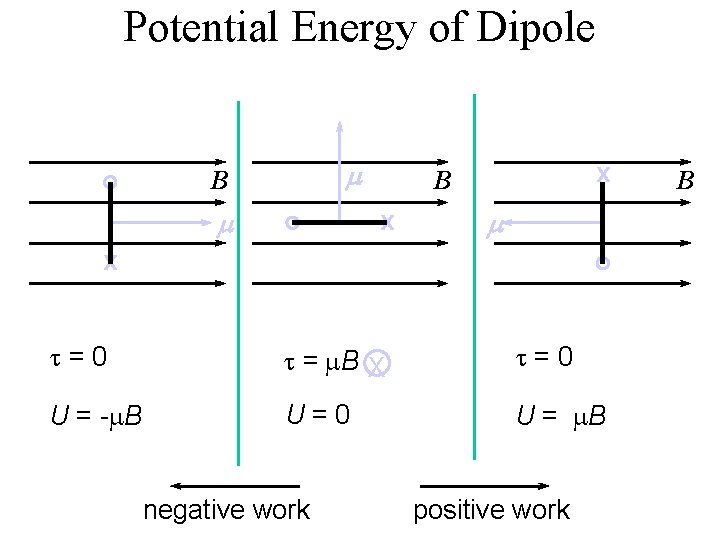
Potential Energy of Dipole • Work must be done to change the orientation of a dipole (current loop) in the presence of a magnetic field. B x q q • Define a potential energy U (with zero at position of max torque) corresponding to this work. Þ Therefore, Þ Þ .

Potential Energy of Dipole m B m x B x m x t=0 t = m. B X t=0 U = -m. B U=0 U = m. B negative work positive work B

Torque Two current carrying loops are oriented in a uniform magnetic field. The loops are nearly identical, except the direction of current is reversed. a) What direction is the torque on loop 1? a) clockwise b) counter-clockwise c) zero b) How does the torque on the two loops compare? a) τ1 > τ2 b) τ1 = τ2 c) τ1 < τ2 c) Which loop occupies a potential energy minimum, and is therefore stable? a) loop 1 b) loop 2 c) the same

Loop 1: m points to the left, so the angle between m and B is equal to 180º, hence t = 0. Loop 2: m points to the right, so the angle between m and B is equal to 0º, hence t = 0. Loop 1: U 1 = +m B Loop 2: U 2 = -m B U 2 is a minimum.

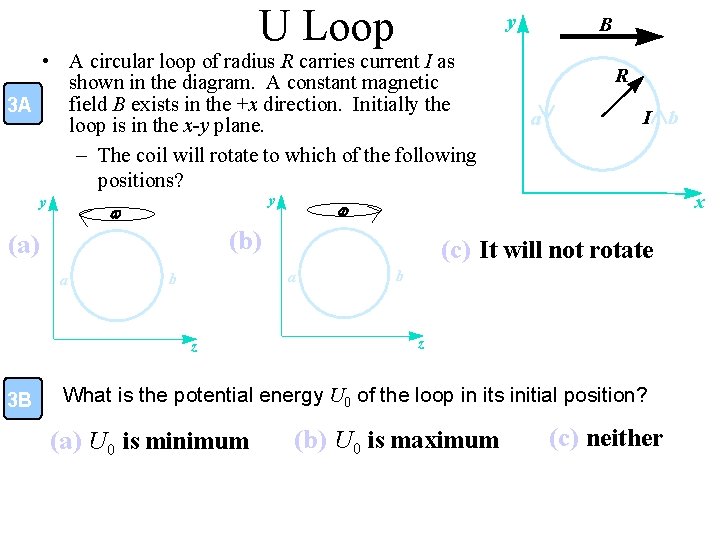
U Loop y • A circular loop of radius R carries current I as shown in the diagram. A constant magnetic field B exists in the +x direction. Initially the 3 A loop is in the x-y plane. – The coil will rotate to which of the following positions? y y w a z 3 B a I b x (c) It will not rotate a b R w (b) (a) B b z What is the potential energy U 0 of the loop in its initial position? (a) U 0 is minimum (b) U 0 is maximum (c) neither

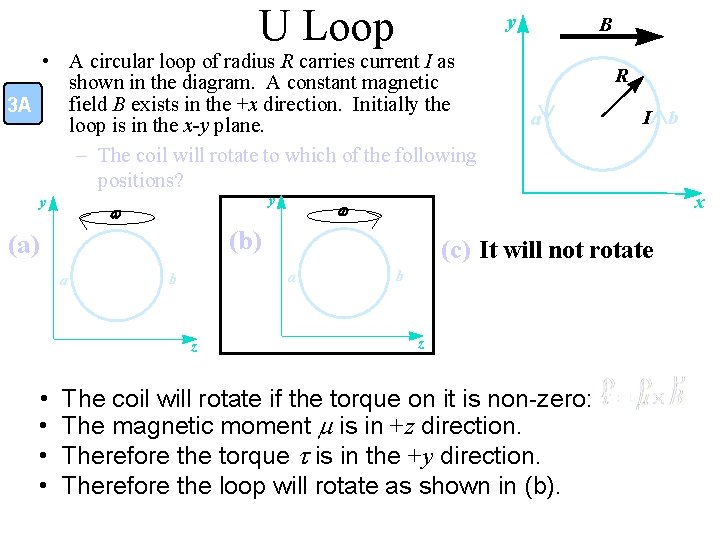
U Loop y • A circular loop of radius R carries current I as shown in the diagram. A constant magnetic field B exists in the +x direction. Initially the 3 A loop is in the x-y plane. – The coil will rotate to which of the following positions? y y w a z • • a I b (c) It will not rotate a b R w (b) (a) B b z The coil will rotate if the torque on it is non-zero: The magnetic moment m is in +z direction. Therefore the torque t is in the +y direction. Therefore the loop will rotate as shown in (b). x

U Loop • A circular loop of radius R carries current I as shown in the diagram. A constant magnetic field B exists in the +x direction. Initially the 3 B loop is in the x-y plane. – What is the potential energy U 0 of the loop in its initial position? (a) U 0 is minimum (b) U 0 is maximum y B R a I b x (c) neither – The potential energy of the loop is given by: – In its initial position, the loop’s magnetic moment vector points in the +z direction, so initial potential energy is ZERO – This does NOT mean that the potential energy is a minimum!!! – When the loop is in the y-z plane and its magnetic moment points in the same direction as the field, its potential energy is NEGATIVE and is in fact the minimum. – Since U 0 is not minimum, the coil will rotate, converting potential energy to kinetic energy!

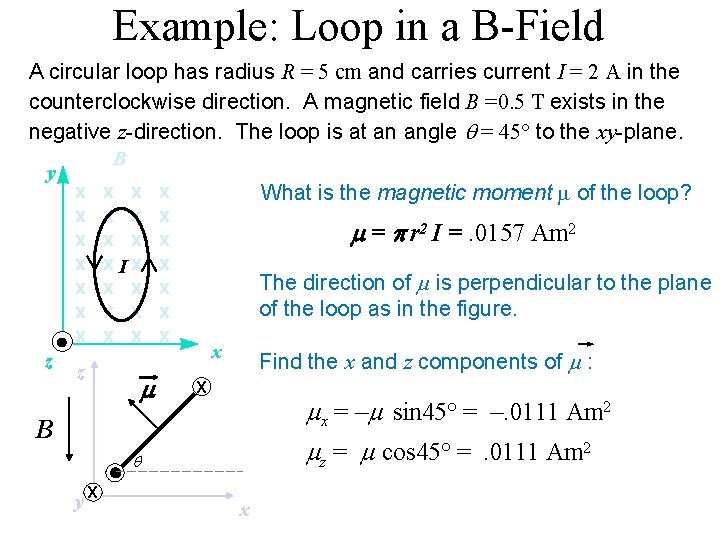
Example: Loop in a B-Field A circular loop has radius R = 5 cm and carries current I = 2 A in the counterclockwise direction. A magnetic field B =0. 5 T exists in the negative z-direction. The loop is at an angle q = 45 to the xy-plane. y z B x x x x z x x x x Ix x x x m What is the magnetic moment m of the loop? x x x x m = p r 2 I =. 0157 Am 2 The direction of m is perpendicular to the plane of the loop as in the figure. x Find the x and z components of m : X mx = –m sin 45 = –. 0111 Am 2 B mz = m cos 45 =. 0111 Am 2 q y X x