Chapter 2 The First Law Unit 5 state

















- Slides: 26

Chapter 2 The First Law Unit 5 state function and exact differentials Spring 2009

State function and Path function • State function a property that is independent of how a sample is prepared. example : T, P, U, H … • Path function a property that is dependent on the preparation of the state. depends on the path between the initial and final states example : W, q …

Example 2. 7 Calculating work, heat, and internal energy • Consider a perfect gas inside a cylinder fitted with a piston. Let the initial state be T, Vi and the final state be T, Vf. The change of state can be brought about in many ways, of which the two simplest are the following: Path 1, in which there is free expansion against zero external pressure; Path 2, in which there is reversible, isothermal expansion. Calculate w, q, and ∆U and DHfor each process.

Example 2. 7 • Path 1 isothermal free expansion Isothermal DU=0, DH=0 DU=q+w = 0 q=-w free expansion w = 0, q=0 • Path 2 isothermal reversible expansion Isothermal DU=0, DH=0 DU=q+w = 0 q=-w reversible expansion

Self Test 2. 8 • Calculate the values of q, w, and ∆U, DH for an irreversible isothermal expansion of a perfect gas against a constant nonzero external Irreversible isothermal expansion Isothermal DU=0, DH=0 DU=q+w = 0 q=-w Irreversible expansion w = - Pex DV , q= Pex DV

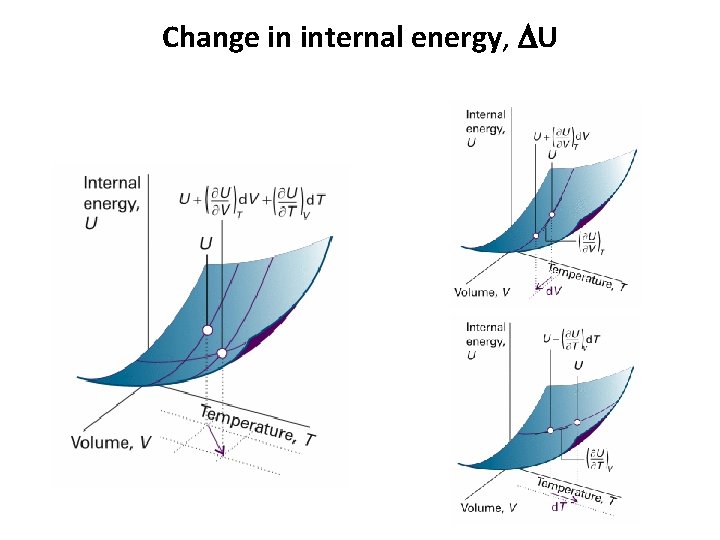
Change in internal energy, DU

Change in internal energy, DU Internal pressure Constant-pressure heat capacity

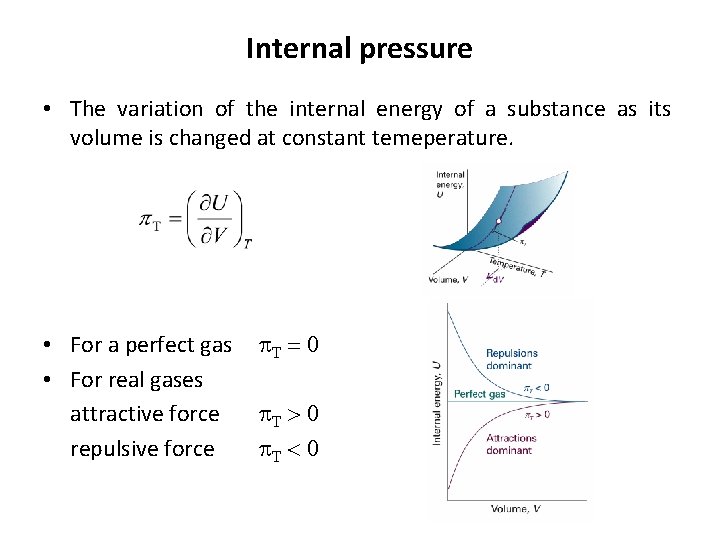
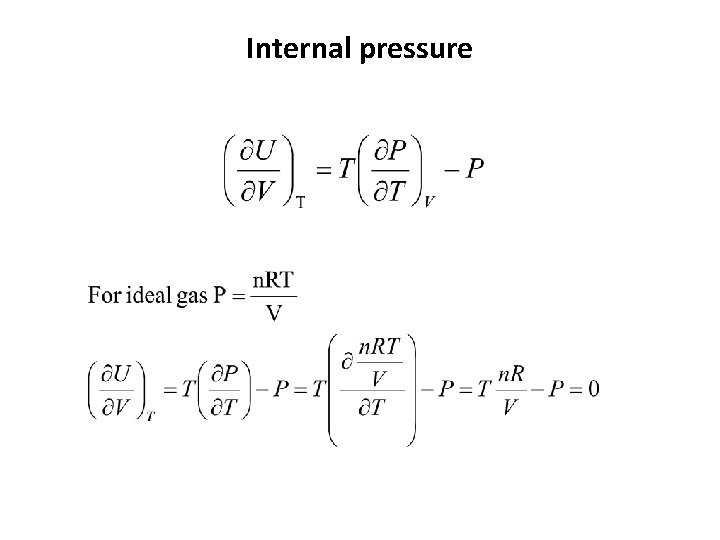
Internal pressure • The variation of the internal energy of a substance as its volume is changed at constant temeperature. • For a perfect gas p. T = 0 • For real gases attractive force p. T > 0 repulsive force p. T < 0

Internal pressure

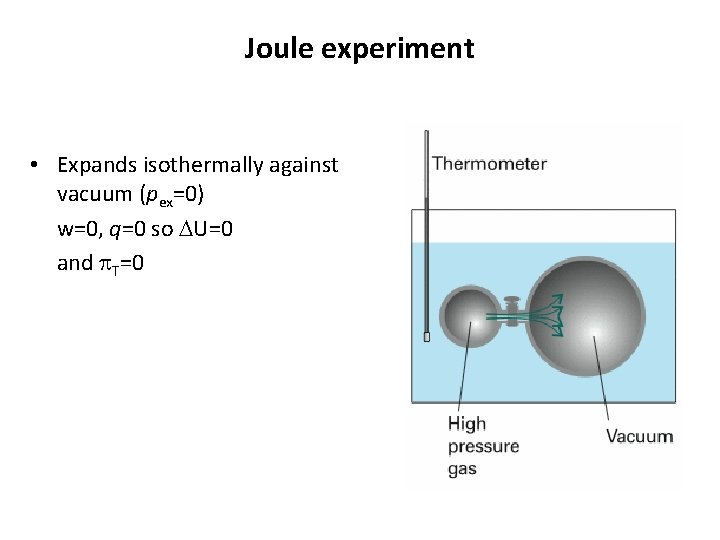
Joule experiment • Expands isothermally against vacuum (pex=0) w=0, q=0 so DU=0 and p. T=0

DU at constant pressure • Expansion coefficient (a): the fraction change in volume with a rise in temperature • Isothermal compressibility (k. T): the fractional change in volumewhen the pressure increases in small amount

E 2. 32 b • The isothermal compressibility of lead at 293 K is 2. 21 × 10− 6 atm− 1. Calculate the pressure that must be applied in order to increase its density by 0. 08 per cent.

Example 2. 8 Calculating the expansion coefficient of a gas Derive an expression for the expansion coefficient of a perfect gas.

DU at constant pressure • For perfect gas p. T = 0,

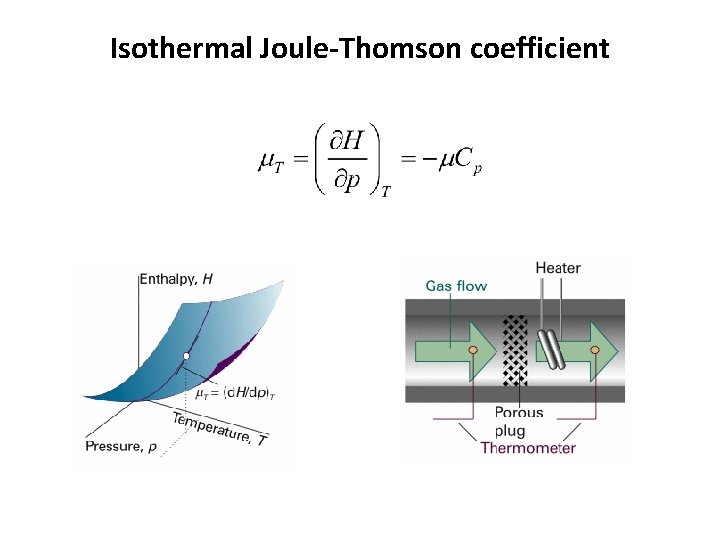
Change in enthalpy, DH (chain relation) Joule-Thomson coefficient m =

Joule-Thomson coefficient, m • A vapour at 22 atm and 5°C was allowed to expand adiabatically to a final pressure of 1. 00 atm; the temperature fell by 10 K. Calculate the Joule–Thomson coefficient, µ, at 5°C, assuming it remains constant over this temperature range.

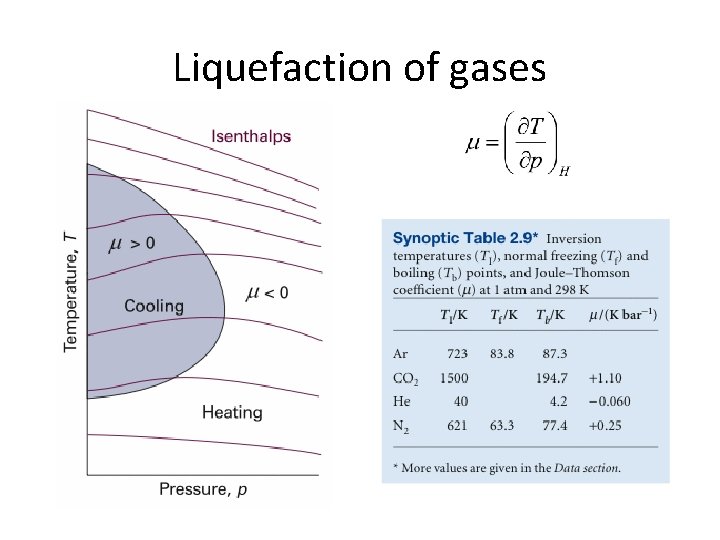
Joule-Thomson coefficient, m • For perfect gases m = 0 • For real gases m > 0 gas cools on expansion m < 0 gas heats on expansion • Inversion temperature

Exercise 2. 29 a • When a certain freon used in refrigeration was expanded adiabatically from an initial pressure of 32 atm and 0°C to a final pressure of 1. 00 atm, the temperature fell by 22 K. Calculate the Joule–Thomson coefficient, µ, at 0°C, assuming it remains constant over this temperature range.

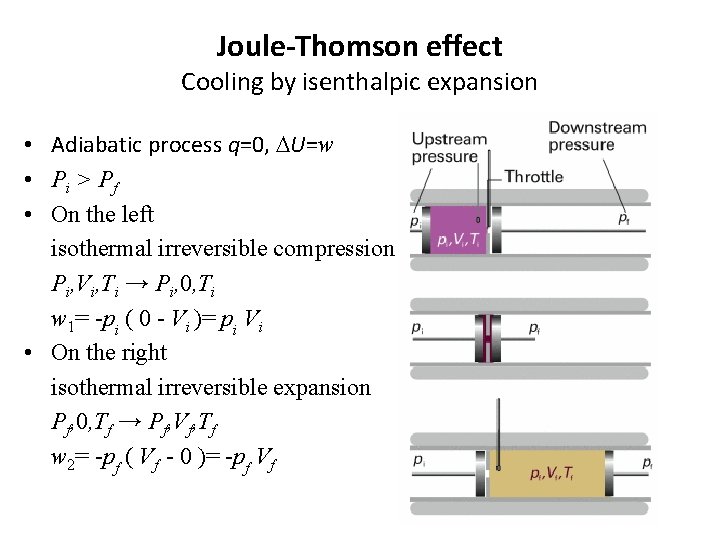
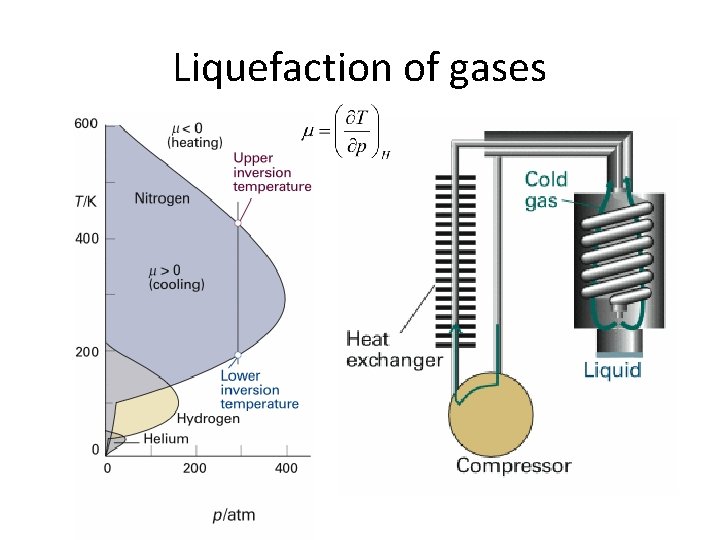
Joule-Thomson effect Cooling by isenthalpic expansion • Adiabatic process q=0, DU=w • Pi > P f • On the left isothermal irreversible compression Pi, Vi, Ti → Pi, 0, Ti w 1= -pi ( 0 - Vi )= pi Vi • On the right isothermal irreversible expansion Pf, 0, Tf → Pf, Vf, Tf w 2= -pf ( Vf - 0 )= -pf Vf

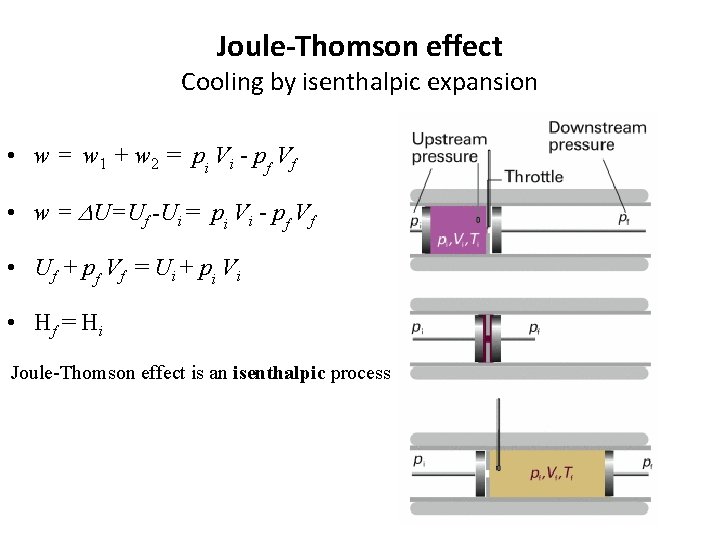
Joule-Thomson effect Cooling by isenthalpic expansion • w = w 1 + w 2 = pi Vi - pf Vf • w = DU=Uf -Ui = pi Vi - pf Vf • Uf + pf Vf = Ui + pi Vi • Hf = H i Joule-Thomson effect is an isenthalpic process

Isothermal Joule-Thomson coefficient

Liquefaction of gases

Liquefaction of gases

Review 1 • Define internal pressure p. T • Prove that, for ideal gas, p. T = 0

Review 2 • Define Expansion coefficient a • Define Isothermal compressibility k. T • Prove that for ideal gas a= 1/T k. T= 1/p

Review 3 • Define Joule-Thomsom coefficient • Prove that Joule-Thomson experiment is an isentahlpic process. • Explain the principle of using Joule-Thomson effect to liquefy gases.
 Newton's first law and second law and third law
Newton's first law and second law and third law Si unit of newton's first law
Si unit of newton's first law Steady flow process in thermodynamics
Steady flow process in thermodynamics V=k/p
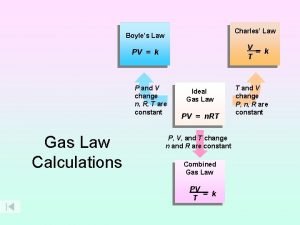
V=k/p Avogadro's law constant
Avogadro's law constant The fbla-pbl national center is located where?
The fbla-pbl national center is located where? Unit 6 review questions
Unit 6 review questions Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Tư thế worm breton là gì
Tư thế worm breton là gì Chúa sống lại
Chúa sống lại Kể tên các môn thể thao
Kể tên các môn thể thao Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Cong thức tính động năng
Cong thức tính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Phép trừ bù
Phép trừ bù độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi