Chapter 14 Recursion Copyright 2012 Pearson AddisonWesley All












![Recursive Binary Search on array[b: e] 1)Get the middle element array[m], m = (left-right)/2 Recursive Binary Search on array[b: e] 1)Get the middle element array[m], m = (left-right)/2](https://slidetodoc.com/presentation_image/6318ff5184ebfb26355716cdd3541d9c/image-17.jpg)
![Binary Search int r. Binary. Search(int sorted. Array[], int first, int last, int key) Binary Search int r. Binary. Search(int sorted. Array[], int first, int last, int key)](https://slidetodoc.com/presentation_image/6318ff5184ebfb26355716cdd3541d9c/image-18.jpg)





























































![Binary Search Problem Definition (cont. ) Pre and Postconditions for the function: //precondition: a[0] Binary Search Problem Definition (cont. ) Pre and Postconditions for the function: //precondition: a[0]](https://slidetodoc.com/presentation_image/6318ff5184ebfb26355716cdd3541d9c/image-85.jpg)






















- Slides: 115

Chapter 14 Recursion Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

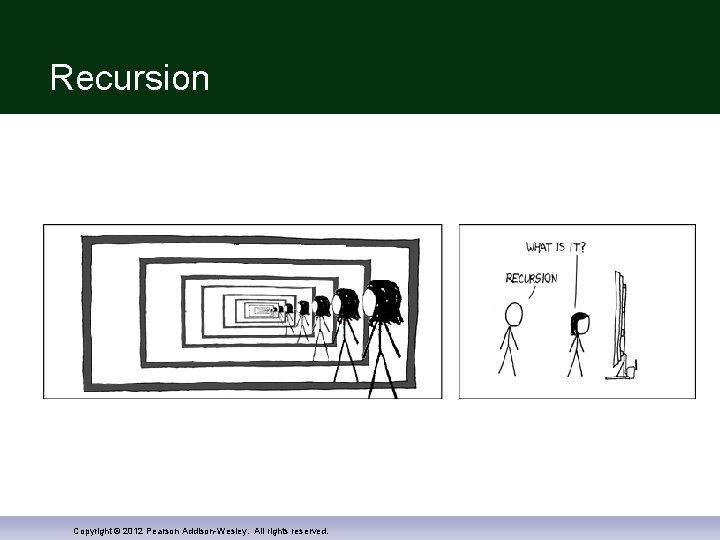
Recursion Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Nesting Dolls Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

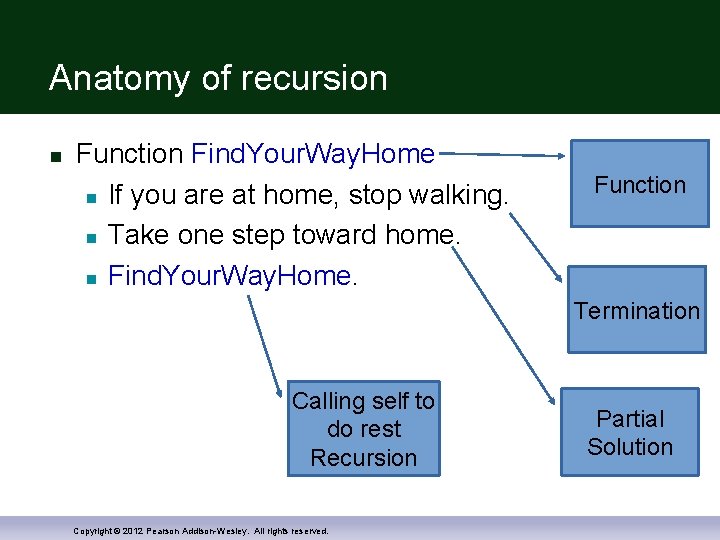
What is recursion? Recursion is the process of defining a problem (or the solution to a problem) in terms of (a simpler version of) itself. For example, we can define the operation Find. Your. Way. Home as: 1)If you are at home, stop walking. 2)Take one step toward home. 3)Find. Your. Way. Home. Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Anatomy of recursion Function Find. Your. Way. Home If you are at home, stop walking. Take one step toward home. Find. Your. Way. Home. Function Termination Calling self to do rest Recursion Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Partial Solution

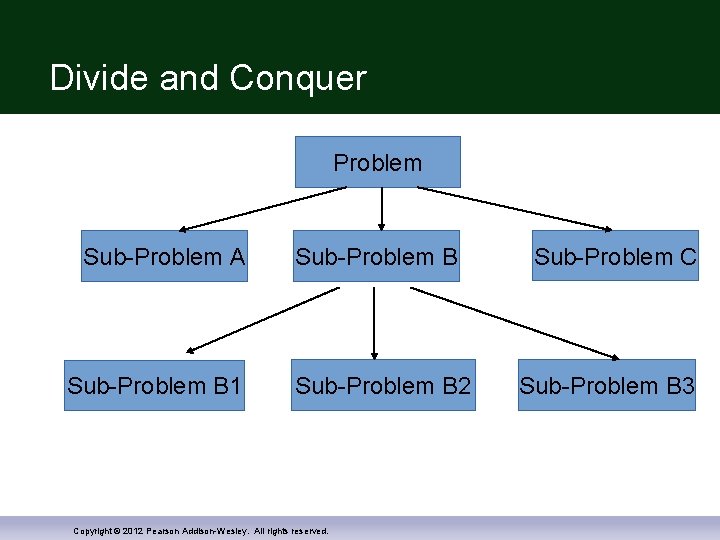
Divide and Conquer Problem Sub-Problem A Sub-Problem B 1 Sub-Problem B 2 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Sub-Problem C Sub-Problem B 3

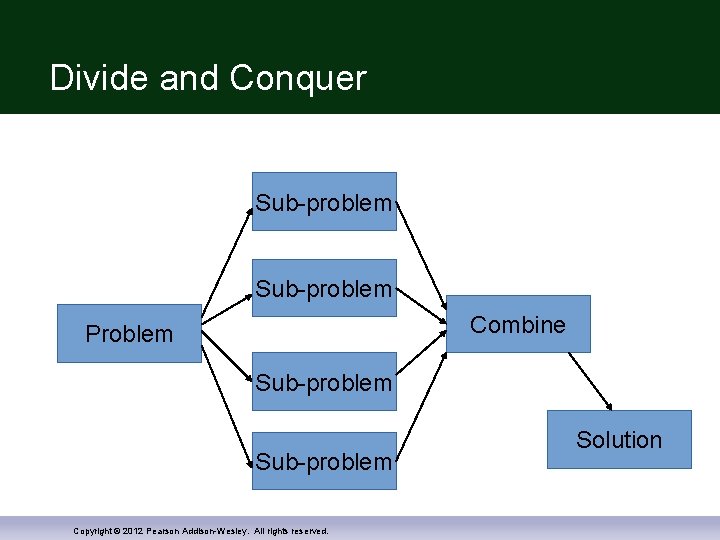
Divide and Conquer 1) Divide: Break the given problem into subproblems of the same type 2) Conquer: Recursively solve these subproblems 3) Combine: Appropriately combine the answers Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Divide and Conquer Sub-problem Combine Problem Sub-problem Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Solution

Example A heavy gold ring is baked in a loaf of bread – how can we find it with minimal cuts? ? Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Example A heavy gold ring is baked in a loaf of bread – how can we find it with minimal cuts? Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Example Left side heavier: Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Example Cut in half, check left side: Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Example Right side is heavier: Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Example This time it seems pretty even: Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Example Found it!: Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Recursive Divide and Conquer Ring Function Find. Ring(bread a_loaf) { Put bread on fulcrum to find the heavy half Cut bread in half If (found the. Ring) { return the. Ring; } return Find. Ring(heavy. Half); } Copyright © 2012 Pearson Addison-Wesley. All rights reserved.
![Recursive Binary Search on arrayb e 1Get the middle element arraym m leftright2 Recursive Binary Search on array[b: e] 1)Get the middle element array[m], m = (left-right)/2](https://slidetodoc.com/presentation_image/6318ff5184ebfb26355716cdd3541d9c/image-17.jpg)
Recursive Binary Search on array[b: e] 1)Get the middle element array[m], m = (left-right)/2 2)If the array[m] equals the searched value, return m 3)If (right<=left) return -1 (not found) 4)If the searched value < array[m] , do a binary search on array[left: m-1] 5)If the searched value < array[m], do a binary search on array[m+1: right] Copyright © 2012 Pearson Addison-Wesley. All rights reserved.
![Binary Search int r Binary Searchint sorted Array int first int last int key Binary Search int r. Binary. Search(int sorted. Array[], int first, int last, int key)](https://slidetodoc.com/presentation_image/6318ff5184ebfb26355716cdd3541d9c/image-18.jpg)
Binary Search int r. Binary. Search(int sorted. Array[], int first, int last, int key) { if (first <= last) { int mid = (first + last) / 2; if (key == sorted. Array[mid]) { return mid; { else if (key < sorted. Array[mid]) { return r. Binary. Search(sorted. Array, first, mid-1, key); { else { return r. Binary. Search(sorted. Array, mid+1, last, key); { Visualization { return -(first + 1); { Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

How Recursion Ends Eventually one of the recursive calls must not depend on another recursive call Recursive functions are defined as One or more cases where the task is accomplished by using recursive calls to do a smaller version of the task One or more cases where the task is accomplished without the use of any recursive calls These are called base cases or stopping cases Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 19

"Infinite" Recursion A function that never reaches a base case, in theory, will run forever In practice, the computer will often run out of resources and the program will terminate abnormally Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 20

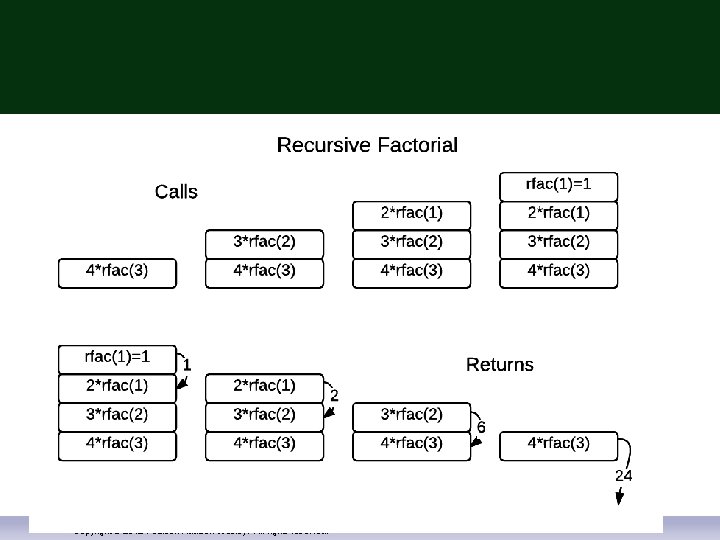
Factorials Iterative n! = n * (n-1) * (n-2) * … * 2 * 1 Recursive Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Factorial Iterative int ifac(int n) { int f=1; while (n>0) { f = f * n; n--; } return f; } Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Recursive int rfac(int n){ if (n==0) return 1; return (n*rfac(n-1)); } Tail Recursion

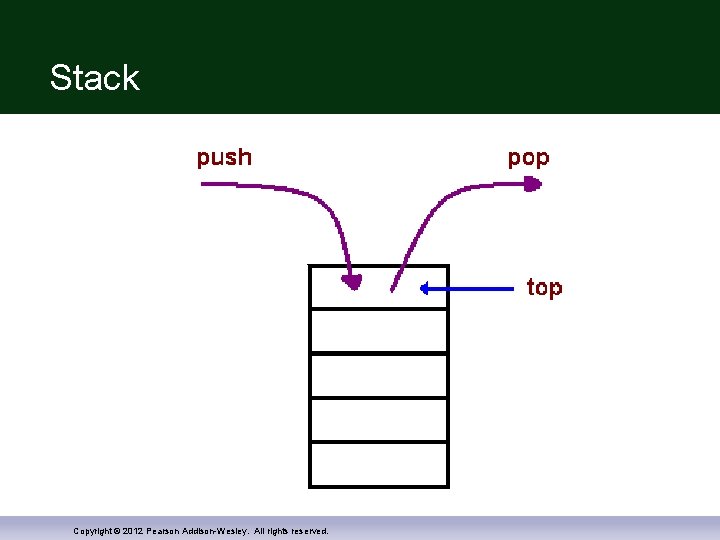
Stacks for Recursion Computers use a structure called a stack to keep track of recursion A stack is a memory structure analogous to a stack of paper To place information on the stack, write it on a piece of paper and place it on top of the stack To place more information on the stack, use a clean sheet of paper, write the information, and place it on the top of the stack To retrieve information, only the top sheet of paper can be read, and thrown away when it is no longer needed Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 23

Stack Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Last-in / First-out A stack is a last-in/first-out memory structure The last item placed is the first that can be removed Whenever a function is called, the computer uses a "clean sheet of paper" The function definition is copied to the paper The arguments are plugged in for the parameters The computer starts to execute the function body Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 25

Stacks and The Recursive Call When a function is called a new activation frame is created on the stack for that function – An activation frame keeps track of the state of the current function (local variables, current line being executed) When a function calls itself, the current activation frame remembers the current line, and a new activation frame is created for the new instance. When the recursive function returns, it's activation frame is discarded, and the result is returned to the calling function. Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 26

Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

The Stack and Ending Recursive Calls When a recursive function does not need to call itself further, but can compute the result locally. Called the base case or termination condition. This final instance of the function returns a value to the previous version, discarding the activation frame. It is a serious problem if the function never reaches a termination condition. Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 28

Stack Overflow Because each recursive call causes an activation frame to be placed on the stack infinite recursion can force the stack to grow beyond its limits to accommodate all the activation frames required The result is a stack overflow A stack overflow causes abnormal termination of the program Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 29

Recursion versus Iteration Any task that can be accomplished using recursion can also be done without recursion A non-recursive version of a function typically contains a loop or loops A non-recursive version of a function is usually called an iterative-version A recursive version of a function Usually runs slower Uses more storage May use code that is easier to write and understand Copyright © 2012 Pearson Addison-Wesley. All rights reserved. non Slide 14 - 30

The Euclidean algorithm, which computes the greatest common divisor of two integers, can be written recursively. Function definition: Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Greatest common divisor gcd(27, 9) = gcd(9, 27% 9) = gcd(9, 0) =9 Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Greatest common divisor int gcd(int x, int y) { if (y == 0) return x; return gcd(y, x%y); } Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Greatest common divisor gcd(111, 259) = gcd(259, 111% 259) = gcd(259, 111) = gcd(111, 259% 111) = gcd(111, 37) = gcd(37, 111% 37) = gcd(37, 0) = 37 Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

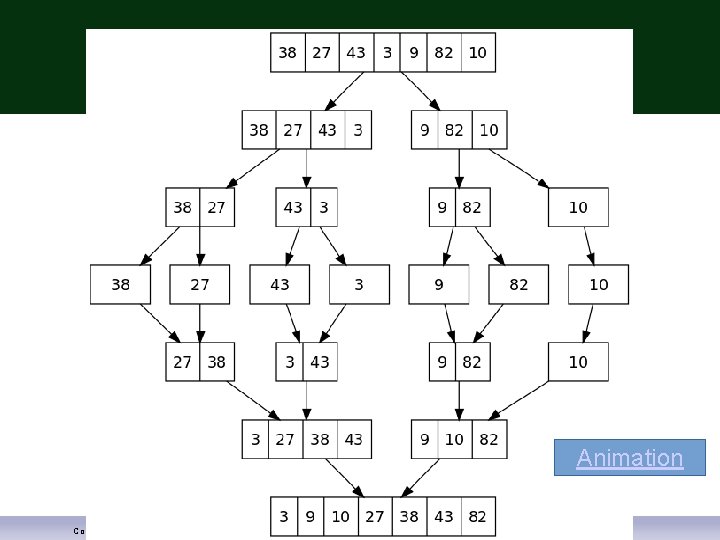
Merge Sort – Recursive Sorting Base Case: A list of length 1 or length 0 is already sorted Recursive Case: Split the list in half Recursively sort two halves Merge sorted halves together Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Animation Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Merge sort Example: Sample Code Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Recursion Towers of Hanoi Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

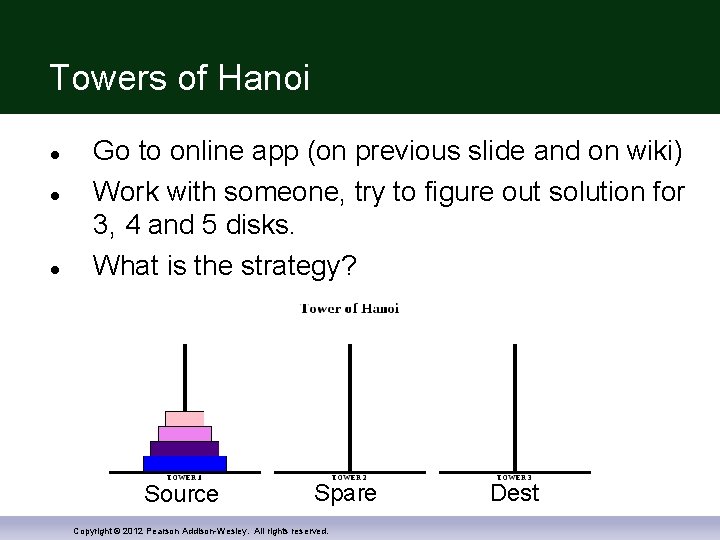
Towers of Hanoi The objective is to transfer the entire tower to one of the other pegs (the rightmost one in the applet below), moving only one disk at a time and never a larger one onto a smaller. Link Source Spare Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Dest

Towers of Hanoi Go to online app (on previous slide and on wiki) Work with someone, try to figure out solution for 3, 4 and 5 disks. What is the strategy? Source Spare Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Dest

Towers of Hanoi 1) Move the top N - 1 disks from Tower 1 to Tower 2 (using Tower 3 as an intermediary peg) 2) Move the bottom disk from Tower 1 to Tower 2 3) Move N - 1 disks from Tower 2 to Tower 3 (using Tower 1 as an intermediary peg) Source Spare Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Dest

Towers of Hanoi Solve(N, Source, Spare, Dest) if N is 0 exit else Solve(N - 1, Source, Dest, Spare) Move from Source to Dest Solve(N - 1, Spare, Source, Dest) Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Towers of Hanoi void hanoi(int disk. Size, int source, int spare, int dest) { if (disk. Size < 1) return; hanoi(disk. Size - 1, source, dest, spare); //Move the remaining disk to the destination peg. cout << "Move disk " << disk. Size; cout << " from peg " << source; cout << " to peg " << dest << endl; Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Towers of Hanoi int main() { //Move all 3 disks from peg 1 to peg 2 using //peg 2 as a temporary. hanoi(3, 1, 2, 3); return 0; } http: //ideone. com/a. Nf 6 Ot Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Towers of Hanoi complexity Can we compute the number of moves in general without actually doing it? Need to solve the “recurrence relation” Len TN be the minimum number of moves for N disks. 1 T 1 = 3 T 2 = 7 T 3 = 15 T 4 = Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Towers of Hanoi complexity Len TN be the minimum number of moves for N disks. T 1 = 1 T 2 = 3 T 3 = 7 The recursive solution involves moving twice (N - 1) disks from one peg to another and making one additional move in between. Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Towers of Hanoi complexity TN = TN-1 + TN-1 = 2 TN-1 + 1 Thus T 0 = 0 TN = 2 TN-1 + 1 for N > 0 Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Towers of Hanoi complexity T 0 = 0 TN = 2 TN-1 + 1 for N > 0 Let SN = TN + 1. Then S 0 = 1 and SN = TN + 1 = (2 TN-1 + 1) + 1 = 2 TN-1 + 2 = 2(TN-1 + 1) = 2 SN-1 SN = 2 SN-1, or it doubles each time. So TN = 2 N - 1 for N ≥ 0. Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

14. 1 Recursive Functions for Tasks Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Recursive Functions for Tasks A recursive function contains a call to itself When breaking a task into subtasks, it may be that the subtask is a smaller example of the same task Searching an array could be divided into searching the first and second halves of the array Searching each half is a smaller version of searching the whole array Tasks like this can be solved with recursive functions Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 50

Case Study: Vertical Numbers Problem Definition: void write_vertical( int n ); //Precondition: n >= 0 //Postcondition: n is written to the screen vertically // with each digit on a separate line Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 51

Case Study: Vertical Numbers Algorithm design: Simplest case: If n is one digit long, write the number Typical case: 1) Output all but the last digit vertically 2) Write the last digit Step 1 is a smaller version of the original task Step 2 is the simplest case Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 52

Case Study: Vertical Numbers (cont. ) The write_vertical algorithm: if (n < 10) { cout << n << endl; } else // n is two or more digits long { write_vertical(n with the last digit removed); cout << the last digit of n << endl; } Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 53

Case Study: Vertical Numbers (cont. ) Translating the pseudocode into C++ n / 10 returns n with the last digit removed n % 10 returns the last digit of n 124 / 10 = 12 124 % 10 = 4 Removing the first digit would be just as valid for defining a recursive solution It would be more difficult to translate into C++ Display 14. 1 ( 1 ) Display 14. 1 ( 2 ) Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 54

Tracing a Recursive Call write_vertical(123) if (123 < 10) { cout << 123 << endl; } Calls write_vertical(12) else // n is more than two digits resume { write_vertical(123/10); cout << (123 % 10) << endl; } Function call ends Output 3 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 55

Tracing write_vertical(12) if (12 < 10) { cout << 12 << endl; } Calls write_vertical(1) else // n is more than two digits resume { write_vertical(12/10); cout << (12 % 10) << endl; } Output 2 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Function call ends Slide 14 - 56

Tracing write_vertical(1) Simplest case is now true if (1 < 10) { cout << 1 << endl; Function call ends } Output 1 else // n is more than two digits { write_vertical(1/10); cout << (1 % 10) << endl; } Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 57

A Closer Look at Recursion write_vertical uses recursion Used no new keywords or anything "new" It simply called itself with a different argument Recursive calls are tracked by Temporarily stopping execution at the recursive call The result of the call is needed before proceeding Saving information to continue execution later Evaluating the recursive call Resuming the stopped execution Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 58

How Recursion Ends Eventually one of the recursive calls must not depend on another recursive call Recursive functions are defined as One or more cases where the task is accomplished by using recursive calls to do a smaller version of the task One or more cases where the task is accomplished without the use of any recursive calls These are called base cases or stopping cases Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 59

"Infinite" Recursion A function that never reaches a base case, in theory, will run forever In practice, the computer will often run out of resources and the program will terminate abnormally Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 60

Example: Infinite Recursion Function write_vertical, without the base case void new_write_vertical(int n) { new_write_vertical (n /10); cout << n % 10 << endl; } will eventually call write_vertical(0), which will call write_vertical(0), which will call write_vertical (0), … Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 61

Stacks for Recursion Computers use a structure called a stack to keep track of recursion A stack is a memory structure analogous to a stack of paper To place information on the stack, write it on a piece of paper and place it on top of the stack To place more information on the stack, use a clean sheet of paper, write the information, and place it on the top of the stack To retrieve information, only the top sheet of paper can be read, and thrown away when it is no longer needed Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 62

Last-in / First-out A stack is a last-in/first-out memory structure The last item placed is the first that can be removed Whenever a function is called, the computer uses a "clean sheet of paper" The function definition is copied to the paper The arguments are plugged in for the parameters The computer starts to execute the function body Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 63

Stacks and The Recursive Call When execution of a function definition reaches a recursive call Execution stops Information is saved on a "clean sheet of paper" to enable resumption of execution later This sheet of paper is placed on top of the stack A new sheet is used for the recursive call A new function definition is written, and arguments are plugged into parameters Execution of the recursive call begins Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 64

The Stack and Ending Recursive Calls When a recursive function call is able to complete its computation with no recursive calls The computer retrieves the top "sheet of paper" from the stack and resumes computation based on the information on the sheet When that computation ends, that sheet of paper is discarded and the next sheet of paper on the stack is retrieved so that processing can resume The process continues until no sheets remain in the stack Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 65

Activation Frames The computer does not use paper Portions of memory are used The contents of these portions of memory is called an activation frame The activation frame does not actually contain a copy of the function definition, but references a single copy of the function Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 66

Stack Overflow Because each recursive call causes an activation frame to be placed on the stack infinite recursion can force the stack to grow beyond its limits to accommodate all the activation frames required The result is a stack overflow A stack overflow causes abnormal termination of the program Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 67

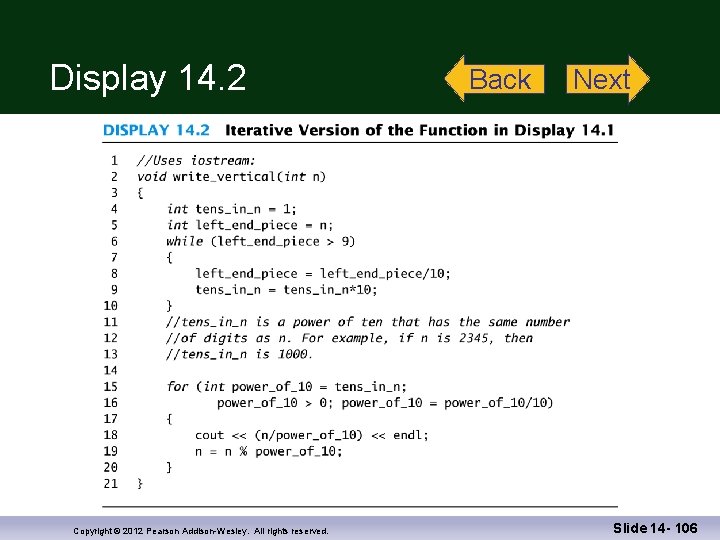
Recursion versus Iteration Any task that can be accomplished using recursion can also be done without recursion A nonrecursive version of a function typically contains a loop or loops A non-recursive version of a function is usually called an iterative-version A recursive version of a function Usually runs slower Uses more storage May use code that is easier to write and understand Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Display 14. 2 Slide 14 - 68

Section 14. 1 Conclusion Can you Identify a possible source of a stack overflow error? Write a recursive void-function with one parameter, a positive integer, that writes out that number of '*'s to the screen? Write write_vertical so the digits are output in reverse order? Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 69

14. 2 Recursive Functions for Values Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Recursive Functions for Values Recursive functions can also return values The technique to design a recursive function that returns a value is basically the same as what you have already seen One or more cases in which the value returned is computed in terms of calls to the same function with (usually) smaller arguments One or more cases in which the value returned is computed without any recursive calls (base case) Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 71

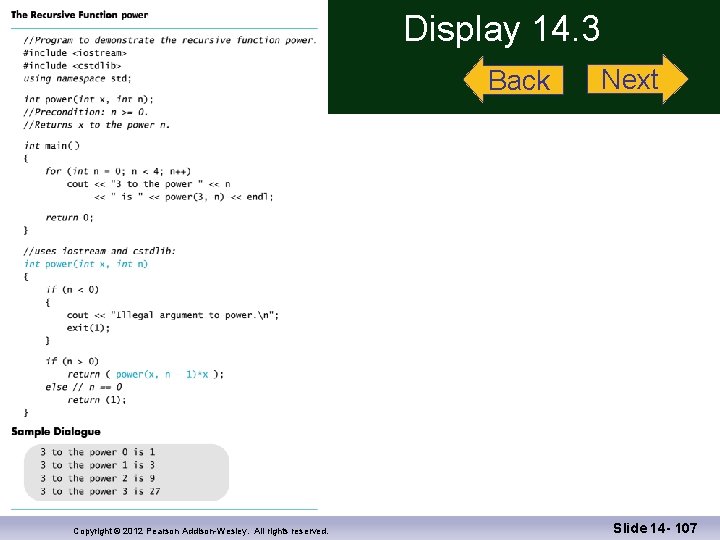
Program Example: A Powers Function To define a new power function that returns an int, such that int y = power(2, 3); places 23 in y Use this definition: Display 14. 3 xn = xn-1 * x Translating the right side to C++ gives: power(x, n-1) * x The base case: n = = 0 and power should return 1 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 72

Tracing power(2, 1) int power(2, 1) { Call to power(2, 0) … if (n > 0) resume return ( power(2, 1 -1) * 2); else 1 return (1); } return 2 Function Ends Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 73

Tracing power(2, 0) int power(2, 0) { … if (n > 0) return ( power(2, 0 -1) * 2); else return (1); Function call ends } 1 is returned Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 74

Tracing power(2, 3) Power(2, 3) results in more recursive calls: power( 2, 3 ) is power( 2, 2 ) * 2 Power( 2, 2 ) is power( 2, 1 ) * 2 Power( 2, 1 ) is power( 2, 0 ) * 2 Power ( 2, 0 ) is 1 (stopping case) See details in Display 14. 4 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 75

Section 14. 2 Conclusion Can you Determine the output of this function if called with rose(4)? int rose(int n) { if ( n <= 0) return 1; else return ( rose (n-1) * n); } Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 76

14. 3 Thinking Recursively Copyright © 2012 Pearson Addison-Wesley. All rights reserved.

Thinking Recursively When designing a recursive function, you do not need to trace out the entire sequence of calls If the function returns a value Check that there is no infinite recursion: Eventually a stopping case is reached Check that each stopping case returns the correct value For cases involving recursion: if all recursive calls return the correct value, then the final value returned is the correct value Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 78

Reviewing the power function There is no infinite recursion Notice that the second argument is decreased at each call. Eventually, the second argument must reach 0, the stopping case int power(int x, int n) { … if (n > 0) return ( power(x, n-1) * x); else return (1); } Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 79

Review of power (cont. ) Each stopping case returns the correct value power(x, 0) should return x 0 = 1 which it does int power(int x, int n) { … if (n > 0) return ( power(x, n-1) * x); else return (1); } Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 80

Review of power (cont. ) All recursive calls return the correct value so the final value returned is correct If n > 1, recursion is used. So power(x, n-1) must return xn-1 so power(x, n) can return xn-1 * n = xn which it does int power(int x, int n) { … if (n > 0) return ( power(x, n-1) * x); else return (1); } Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 81

Recursive void-functions The same basic criteria apply to checking the correctness of a recursive void-function Check that there is no infinite recursion Check that each stopping case performs the correct action for that case Check that for each recursive case: if all recursive calls perform their actions correctly, then the entire case performs correctly Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 82

Case Study: Binary Search A binary search can be used to search a sorted array to determine if it contains a specified value The array indexes will be 0 through final_index Because the array is sorted, we know a[0] <= a[1] <= a[2] <= … <= a[final_index] If the item is in the list, we want to know where it is in the list Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 83

Binary Search: Problem Definition The function will use two call-by-reference parameters to return the outcome of the search One, called found, will be type bool. If the value is found, found will be set to true. If the value is found, the parameter, location, will be set to the index of the value A call-by-value parameter is used to pass the value to find This parameter is named key Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 84
![Binary Search Problem Definition cont Pre and Postconditions for the function precondition a0 Binary Search Problem Definition (cont. ) Pre and Postconditions for the function: //precondition: a[0]](https://slidetodoc.com/presentation_image/6318ff5184ebfb26355716cdd3541d9c/image-85.jpg)
Binary Search Problem Definition (cont. ) Pre and Postconditions for the function: //precondition: a[0] through a[final_index] are // sorted in increasing order //postcondition: if key is not in a[0] - a[final_index] // found == false; otherwise // found == true Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 85

Binary Search Algorithm Design Our algorithm is basically: Look at the item in the middle If it is the number we are looking for, we are done If it is greater than the number we are looking for, look in the first half of the list If it is less than the number we are looking for, look in the second half of the list Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 86

Binary Search Algorithm Design (cont. ) Here is a first attempt at our algorithm: found = false; mid = approx. midpoint between 0 and final_index; if (key == a[mid]) { found = true; location = mid; } else if (key < a[mid]) search a[0] through a[mid -1] else if (key > a[mid]) search a[mid +1] through a[final_index]; Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 87

Binary Search Algorithm Design (cont. ) Since searching each of the shorter lists is a smaller version of the task we are working on, a recursive approach is natural We must refine the recursive calls Because we will be searching subranges of the array, we need additional parameters to specify the subrange to search We will add parameters first and last to indicate the first and last indices of the subrange Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 88

Binary Search Algorithm Design (cont. ) Here is our first refinement: found = false; mid = approx. midpoint between first and last; if (key == a[mid]) { found = true; location = mid; } else if (key < a[mid]) search a[first] through a[mid -1] else if (key > a[mid]) search a[mid +1] through a[last]; Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 89

Binary Search Algorithm Design (cont. ) We must ensure that our algorithm ends If key is found in the array, there is no recursive call and the process terminates What if key is not found in the array? At each recursive call, either the value of first is increased or the value of last is decreased If first ever becomes larger than last, we know that there are no more indices to check and key is not in the array Display 14. 5 The final pseudocode is shown in Display 14. 7 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 90

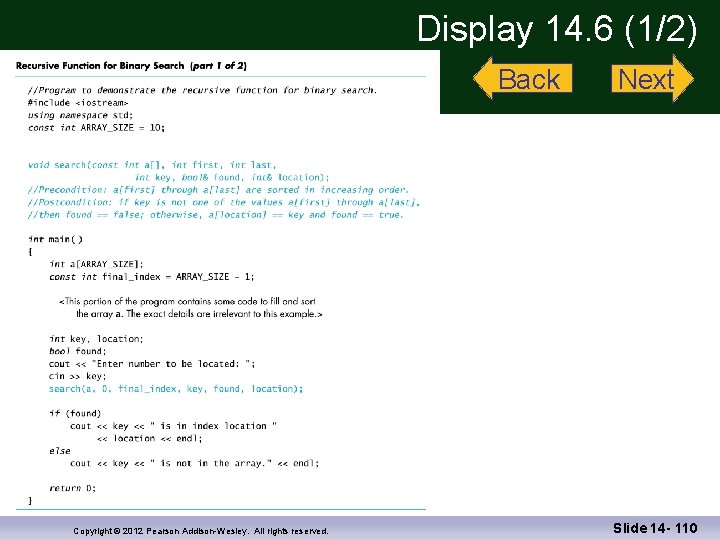
Binary Search Writing the Code Function search implements the algorithm: Function search interface: void search(const int a[ ], int first, int last, int key, bool& found, int& location); //precondition: a[0] through a[final_index] are // sorted in increasing order //postcondition: if key is not in a[0] - a[final_index] // found = = false; otherwise // found = = true Display 14. 6 (1) Display 14. 6 (2) Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 91

Binary Search Checking the Recursion There is no infinite recursion On each recursive call, the value of first is increased or the value of last is decreased. Eventually, if nothing else stops the recursion, the stopping case of first > last will be called Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 92

Binary Search Checking the Recursion (cont. ) Each stopping case performs the correct action If first > last, there are no elements between a[first] and a[last] so key is not in this segment and it is correct to set found to false If k == a[mid], the algorithm correctly sets found to true and location equal to mid Therefore both stopping cases are correct Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 93

Binary Search Checking the Recursion (cont. ) For each case that involves recursion, if all recursive calls perform their actions correctly, then the entire case performs correctly Since the array is sorted… If key < a[mid], key is in one of elements a[first] through a[mid-1] if it is in the array. No other elements must be searched…the recursive call is correct If key > a[mid], key is in one of elements a[mid+1] through a[last] if it is in the array. No other elements must be searched… the recursive call is correct Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 94

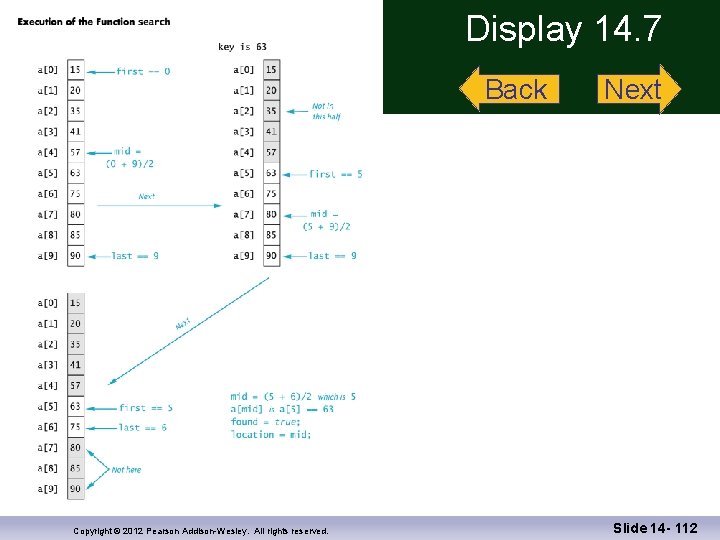
Binary Search Efficiency The binary search is extremely fast compared to an algorithm that checks each item in order The binary search eliminates about half the elements between a[first] and a[last] from consideration at each recursive call For an array of 100 items, the binary search never compares more than seven elements to the key For an array of 100 items, a simple serial search will average 50 comparisons and may do as many as 100! Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 95

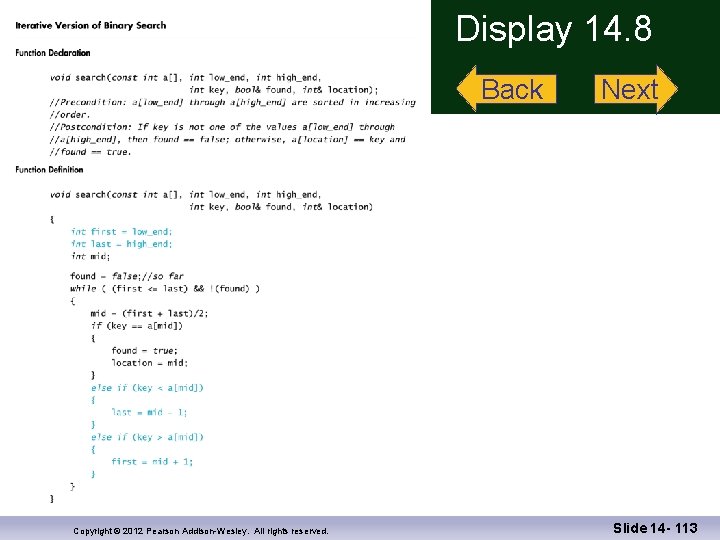
Binary Search An Iterative Version The iterative version of the binary search may be run faster on some systems The algorithm for the iterative version, shown in Display 14. 8, was created by mirroring the recursive function Even if you plan an iterative function, it may be helpful to start with the recursive approach Display 14. 8 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 96

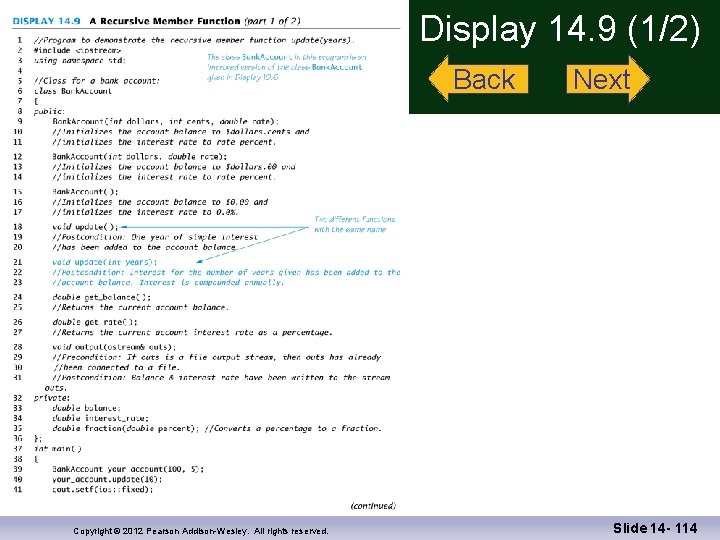
Program Example: A Recursive Member Function A member function of a class can be recursive The update function from class Bank. Account of Display 10. 6 is will be overloaded to create a recursive version Update adds interest for a specified number of years to an account balance Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 97

Class Bank. Account Function update uses one parameter, years, and the following algorithm: If the number of years is 1, then (// stopping case) call the other function named update If the number of years is greater than 1, then Make a recursive call to post years – 1 worth of interest then call the other update function for one year's interest Display 14. 9 (1) Display 14. 9 (2) Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 98

Function update Checking the Recursion There is no infinite recursion Each recursive call reduces the number of years by one until years is 1, a stopping case Each stopping case performs the correct action One stopping case is years == 1. It calls the other update function which was previously checked for correctness Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 99

Function update Checking the Recursion (cont. ) For the cases that involve recursion, if all recursive calls perform correctly, the entire case performs correctly: When years > 1, the recursive call correctly posts years – 1 worth of interest, then calls the other update function to post one additional year's interest. The other update function correctly posts interest for one year. Then the entire action for years > 1 will be correct. Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 100

Overloaded Functions There is no confusion (for the computer) between the two versions of update When the recursive version of update calls the version of update with no parameters, that is not a recursive call Only calls to the version of update with the exact same function declaration are recursive calls Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 101

Section 14. 3 Conclusion Can you Write a recursive function definition for the following function? int squares(int n); //Precondition: n >= 1 //Returns the sum of the squares of numbers 1 through n Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 102

Chapter 14 -- End Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Slide 14 - 103

Display 14. 1 (1/2) Back Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Next Slide 14 - 104

Display 14. 1 (2/2) Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Back Next Slide 14 - 105

Display 14. 2 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Back Next Slide 14 - 106

Display 14. 3 Back Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Next Slide 14 - 107

Display 14. 4 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Back Next Slide 14 - 108

Display 14. 5 Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Back Next Slide 14 - 109

Display 14. 6 (1/2) Back Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Next Slide 14 - 110

Display 14. 6 (2/2) Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Back Next Slide 14 - 111

Display 14. 7 Back Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Next Slide 14 - 112

Display 14. 8 Back Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Next Slide 14 - 113

Display 14. 9 (1/2) Back Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Next Slide 14 - 114

Display 14. 9 (2/2) Back Copyright © 2012 Pearson Addison-Wesley. All rights reserved. Next Slide 14 - 115
 To understand recursion you must understand recursion
To understand recursion you must understand recursion Dentist copyright 2012
Dentist copyright 2012 Copyright 2012
Copyright 2012 Copyright 2012
Copyright 2012 Copyright 2012
Copyright 2012 Pearson education 2012
Pearson education 2012 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc Olecranal region
Olecranal region Pearson education inc. 2012
Pearson education inc. 2012 Pearson 2012
Pearson 2012 Pearson education inc. 2012
Pearson education inc. 2012 2012 pearson education inc anatomy and physiology
2012 pearson education inc anatomy and physiology 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc Pearson education 2012
Pearson education 2012 Pearson education inc. 2012
Pearson education inc. 2012 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc 2012 pearson education inc
2012 pearson education inc 2017 pearson education inc
2017 pearson education inc 2017 pearson education inc
2017 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc 2009 pearson education inc
2009 pearson education inc 2018 pearson education inc
2018 pearson education inc 2014 pearson education inc
2014 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Copyright by pearson education inc. answers
Copyright by pearson education inc. answers 2008 pearson education inc
2008 pearson education inc Copyright 2005 pearson prentice hall inc
Copyright 2005 pearson prentice hall inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc Copyright pearson education inc
Copyright pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Copyright 2010 pearson education inc
Copyright 2010 pearson education inc Pearson education inc all rights reserved
Pearson education inc all rights reserved Copyright 2009 pearson education inc
Copyright 2009 pearson education inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc 2009 pearson education inc
2009 pearson education inc Copyright pearson education inc
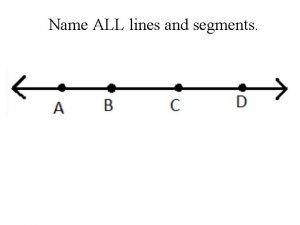
Copyright pearson education inc Draw three noncollinear points j k and l
Draw three noncollinear points j k and l Prentice hall publishing
Prentice hall publishing Pearson education 2011
Pearson education 2011 Pearson vue president
Pearson vue president Stress management for life 5th edition
Stress management for life 5th edition Pearson education inc publishing as pearson prentice hall
Pearson education inc publishing as pearson prentice hall Pearson education inc publishing as pearson prentice hall
Pearson education inc publishing as pearson prentice hall Copyright 2015 all rights reserved
Copyright 2015 all rights reserved Copyright 2015 all rights reserved
Copyright 2015 all rights reserved Dell all rights reserved copyright 2009
Dell all rights reserved copyright 2009 Copyright © 2018 all rights reserved
Copyright © 2018 all rights reserved Pearson education inc. all rights reserved
Pearson education inc. all rights reserved 2010 pearson education inc
2010 pearson education inc 2010 pearson education inc
2010 pearson education inc Vba recursion
Vba recursion Mamdm
Mamdm Recursive pronouns
Recursive pronouns What is recursion in language
What is recursion in language Eliminate left recursion calculator
Eliminate left recursion calculator Tail recursion
Tail recursion Indirect left recursion example
Indirect left recursion example Recursion error fanfic
Recursion error fanfic Iterative vs recursive
Iterative vs recursive Box trace recursion
Box trace recursion Recursion in mathematics
Recursion in mathematics What is recursion can be a powerful tool for solving?
What is recursion can be a powerful tool for solving? How recursion works in java
How recursion works in java Recursion google
Recursion google Recursion time complexity
Recursion time complexity Recursion in java
Recursion in java Linear recursion example
Linear recursion example Box trace recursion
Box trace recursion Ap computer science a recursion
Ap computer science a recursion Prolog recursion
Prolog recursion Box trace recursion
Box trace recursion Recursion time complexity
Recursion time complexity Mips recursion
Mips recursion Left recursion definition
Left recursion definition Recursive algorithm time complexity
Recursive algorithm time complexity Recursion matlab examples
Recursion matlab examples Generative recursion
Generative recursion What is recursion
What is recursion Recursion vs loop
Recursion vs loop Tail recursion in java
Tail recursion in java Recursion
Recursion Tail recursion in java
Tail recursion in java Mips recursion example
Mips recursion example Left recursion
Left recursion Using recursion in models and decision making sheet 3
Using recursion in models and decision making sheet 3 Telic recursion
Telic recursion Recursion tree examples
Recursion tree examples Similarities between iteration and recursion
Similarities between iteration and recursion Python recursion practice
Python recursion practice Recursion in assembly language 8086
Recursion in assembly language 8086 Drawing hands 1948
Drawing hands 1948 Application of recursion
Application of recursion What is inline function
What is inline function Recursive definition of odd positive integers
Recursive definition of odd positive integers Cs106b lectures
Cs106b lectures Selection sort python recursive
Selection sort python recursive Recursion
Recursion Recursion vs dynamic programming
Recursion vs dynamic programming Recursion
Recursion Recursion
Recursion Recursion
Recursion Dynamic programming recursion example
Dynamic programming recursion example