M C Escher Drawing Hands 1948 Recursion Dave

M. C. Escher: "Drawing Hands" (1948)

Recursion Dave Feinberg

Computation n n All computation consists of chugging along from state to state. . . There is a set of rules that tell us, given the current state, which state to go to next.

Arithmetic as Rewrite Rules n 2+3+4 5+4 9 n We stop when we reach a number. n n

Functions as New Rules def square(n): return n * n When we see: square(something) Rewrite it as: something * something

Functions as Rewrite Rules def square(n): return n * n n square(3) 3*3 9

Piecewise Functions f(n) = 1 n-1 f(4) 4 -1 3 if n = 1 if n > 1

In Python def f(n): if n == 1: return 1 else: return n - 1

This is just math, right? n n Difference between mathematical functions and computation functions. Computation functions must be effective. For example, we can define the square-root function as √x = the y such that y ≥ 0 and y² = x n This defines a valid mathematical function, but it doesn't tell us how to compute the square root of a given number.

Fancier Functions def f(n): return n + (n - 1) Find f(4)

Fancier Functions def f(n): return n + (n - 1) def g(n): return n + f(n - 1) Find g(4)

Fancier Functions def f(n): return n + (n - 1) def g(n): return n + f(n - 1) def h(n): return n + h(n - 1) Find h(4)

Recursion def h(n): return n + h(n - 1) n h is a recursive function, because it is defined in terms of itself.

Definition Recursion n See: "Recursion".

Recursion def h(n): return n + h(n - 1) h(4) 4 + h(3) 4 + 3 + h(2) 4 + 3 + 2 + h(1) 4 + 3 + 2 + 1 + h(0) 4 + 3 + 2 + 1 + 0 + h(-1) 4 + 3 + 2 + 1 + 0 + -1 + h(-2). . . Evaluating h leads to an infinite loop!

What you are thinking "Ok, recursion is bad. What's the big deal? "

Recursion def f(n): if n == 1: return 1 else: return f(n - 1) Find f(1) f(2) f(3) f(100)

Recursion def f(n): if n == 1: return 1 else: return f(n - 1) f(3 - 1) f(2 - 1) f(1) 1

Terminology def f(n): if n == 1: return 1 else: return f(n - 1) base case recursive case "Useful" recursive functions have: n at least one recursive case n at least one base case so that the computation terminates

Recursion def f(n): if n == 1: return 1 else: return f(n + 1) Find f(5) We have a base case and a recursive case. What's wrong?

Recursion The recursive case should call the function on a simpler input, bringing us closer and closer to the base case.

Recursion def f(n): if n == 0: return 0 else: return 1 + f(n - 1) Find f(0) f(1) f(2) f(100)

Recursion def f(n): if n == 0: return 0 else: return 1 + f(n - 1) f(3) 1 + f(2) 1 + f(1) 1 + 1 + f(0) 1+1+1+0 3

Factorial n 4! = 4 × 3 × 2 × 1 = 24

Factorial n Does anyone know the value of 9! n 362, 880 n Does anyone know the value of 10! n How did you know?

Factorial n 9! = 9× 8× 7× 6× 5× 4× 3× 2× 1 n 10! = 10 × 9! n n! = n × (n - 1)! n That's a recursive definition!

Factorial def fact(n): return n * fact(n - 1) fact(3) 3 × fact(2) 3 × 2 × fact(1) 3 × 2 × 1 × fact(0) 3 × 2 × 1 × 0 × fact(-1). . .

Factorial n What did we do wrong? n What is the base case for factorial?

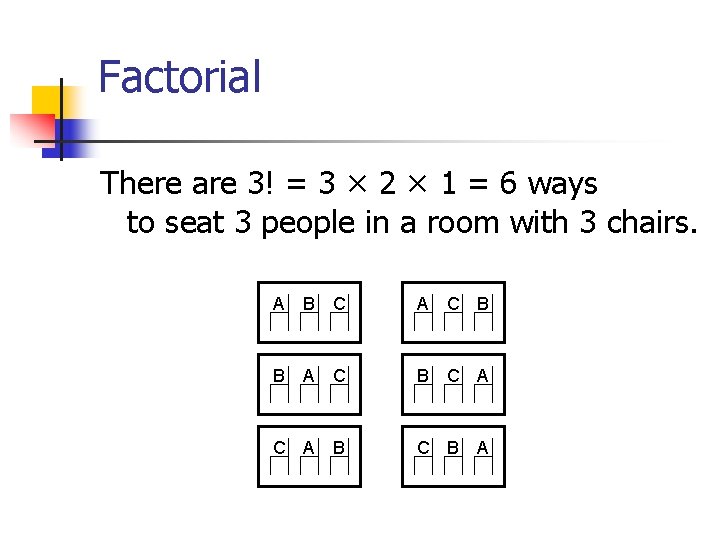
Factorial n! = # of ways to seat n people in a room with n chairs. How many ways are there to seat 3 people in a room with 3 chairs?

Factorial There are 3! = 3 × 2 × 1 = 6 ways to seat 3 people in a room with 3 chairs. A B C A C B B A C B C A B C B A

Factorial There are 2! = 2 × 1 = 2 ways to seat 2 people in a room with 2 chairs. A B B A

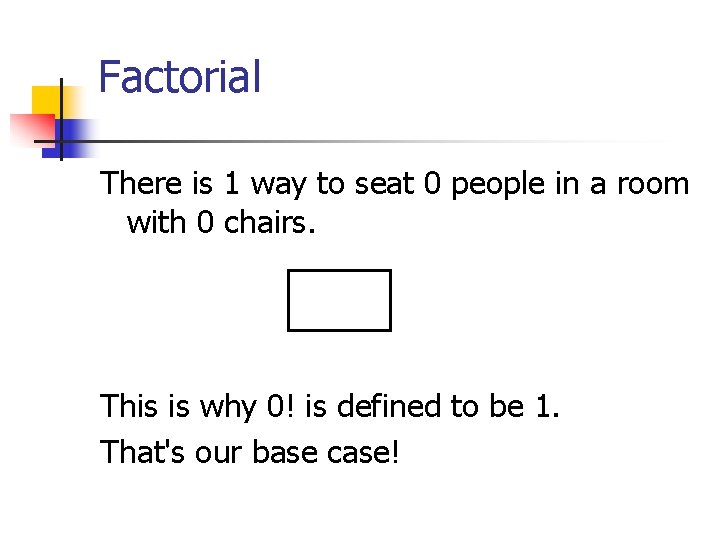
Factorial There is only 1! = 1 way to seat 1 person in a room with 1 chair. A How many ways are there to seat 0 people in a room with 0 chairs?

Factorial There is 1 way to seat 0 people in a room with 0 chairs. This is why 0! is defined to be 1. That's our base case!

Factorial def fact(n): if n == 0: return 1 else: return n * fact(n - 1) fact(3) 3 × fact(2) 3 × 2 × fact(1) 3 × 2 × 1 × fact(0) 3× 2× 1× 1 6

Writing Recursive Functions n n Write if. Why? Base case: Test for and handle simplest case. Recursive case: Call function on simpler input. Assume the recursive call works. How does it help us?

Honey Bees Drone: son of queen Queen: daughter of queen + drone (Worker: daughter of queen + drone)

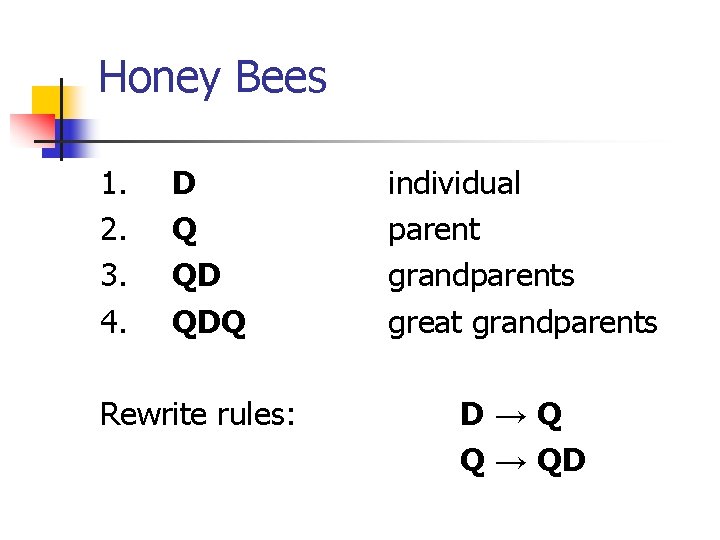
Honey Bees 1. 2. 3. 4. D Q QD QDQ Rewrite rules: individual parent grandparents great grandparents D→Q Q → QD

Honey Bees 1. D individual 2. Q parent 3. QD grandparents 4. QDQ great grandparents 5. QDQQD 6. QDQQDQDQ 7. QDQQDQQD How many in each generation?

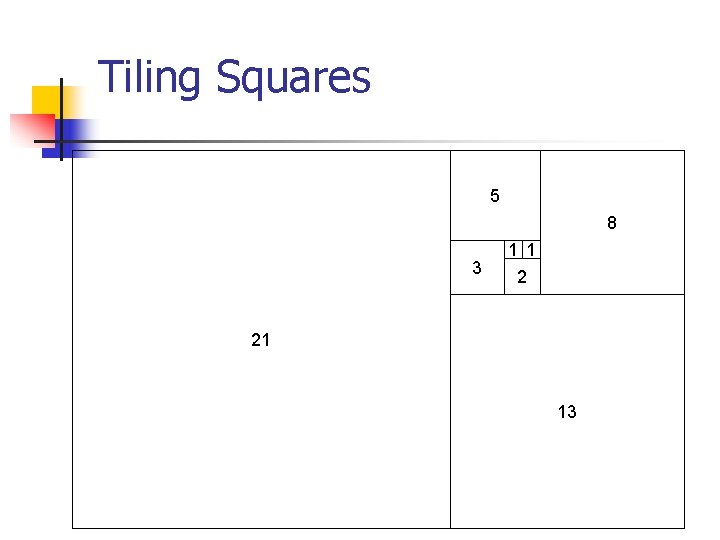
Honey Bees 1. 2. 3. 4. 5. 6. 7. It's D Q QD QDQQDQDQQDQQD the Fibonacci sequence! 1 1 2 3 5 8 13

Fibonacci In the Fibonacci sequence, each term = sum of previous 2 terms Let fib(n) be the nth term. Then, fib(n) = fib(n - 1) + fib(n - 2) The sequence is defined recursively!

Fibonacci def fib(n): return fib(n - 1) + fib(n - 2) Find fib(1) We need a base case!

Fibonacci def fib(n): if n == 1: return 1 else: return fib(n - 1) + fib(n - 2) Find fib(1) Find fib(2) How do we fix our function?

Fibonacci def fib(n): if n <= 2: return 1 else: return fib(n - 1) + fib(n - 2) Find fib(1) Find fib(2) Find fib(3)

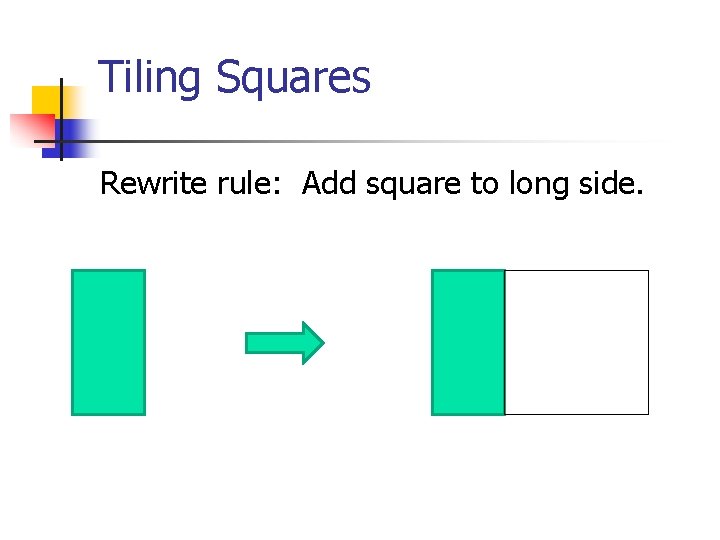
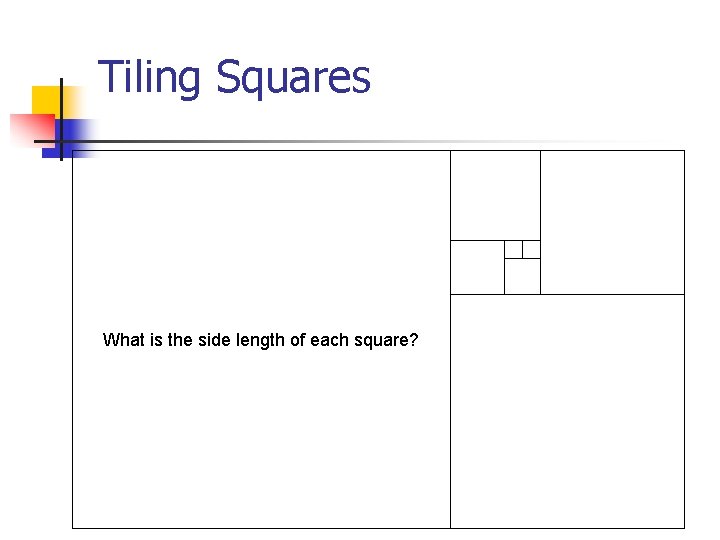
Tiling Squares Rewrite rule: Add square to long side.

Tiling Squares What is the side length of each square?

Tiling Squares 5 8 3 1 1 2 21 13

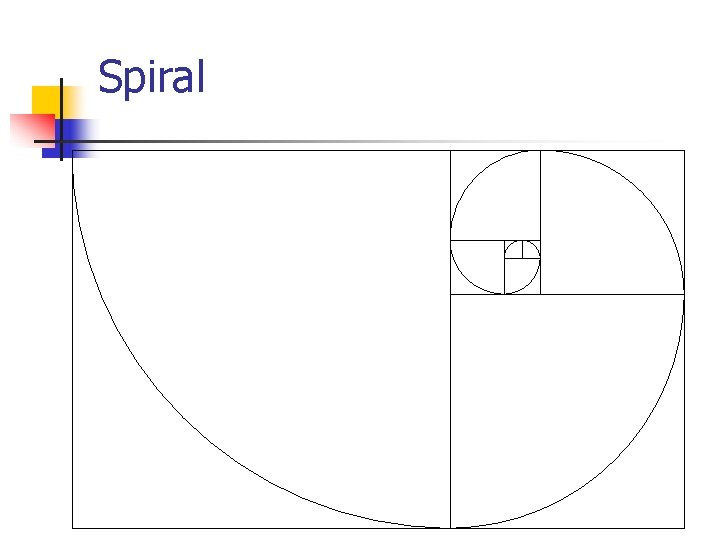
Spiral

Fibonacci 1 2 3 5 8 13 21 34 ÷ ÷ ÷ ÷ 1 = 2 = 3 = 5 = 8 = 13 = 21 = 1 2 1. 5 1. 666. . . 1. 625 1. 615. . . 1. 619. . .

Limit fib(n) What is the limit of fib(n - 1) as n approaches infinity? 1. 6180339887498948482. . . What's that called?

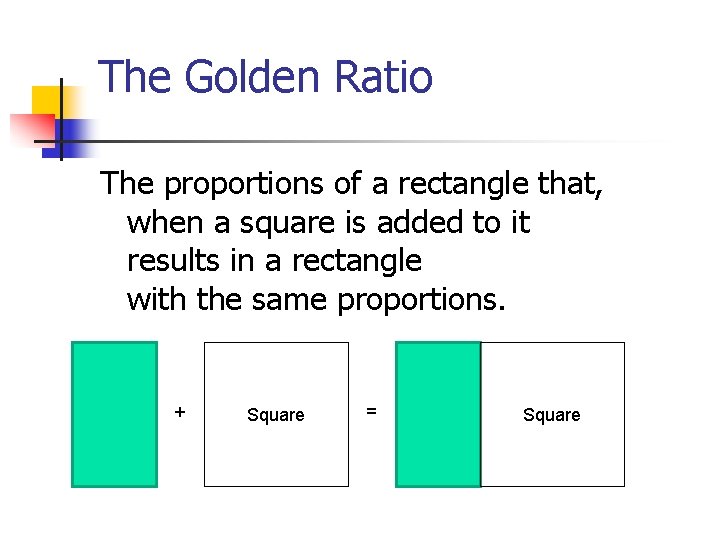
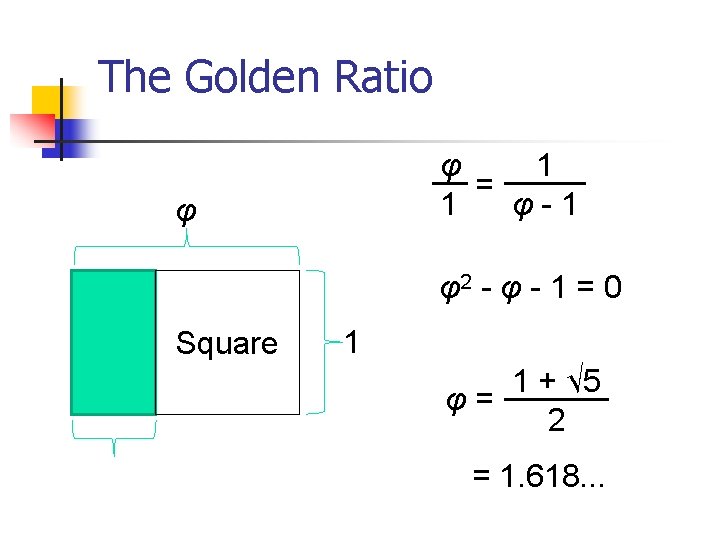
The Golden Ratio The proportions of a rectangle that, when a square is added to it results in a rectangle with the same proportions. + Square = Square

The Golden Ratio φ 1 = 1 φ-1 φ φ2 - φ - 1 = 0 Square 1 1 + √ 5 φ= 2 = 1. 618. . .

Fibonacci fib(n) = 1 n = 1, 2 fib(n-1) + fib(n-2) n > 2 φn - (1 - φ)n fib(n) = √ 5

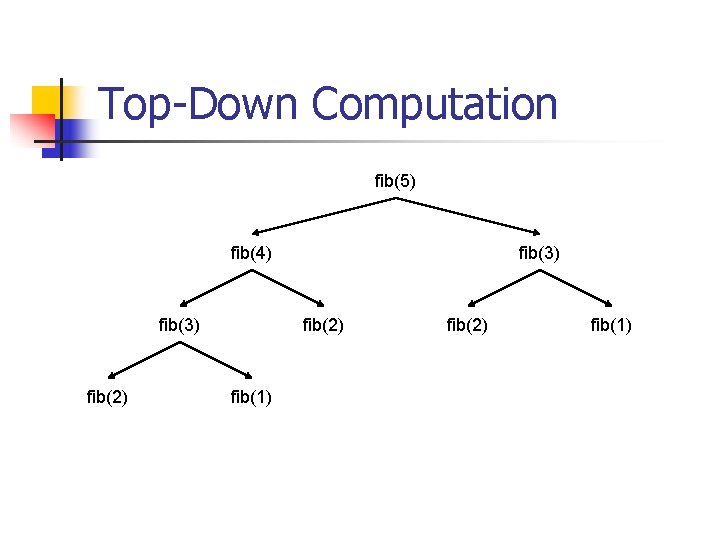
Top-Down Computation fib(5) fib(4) fib(3) fib(2) fib(1)

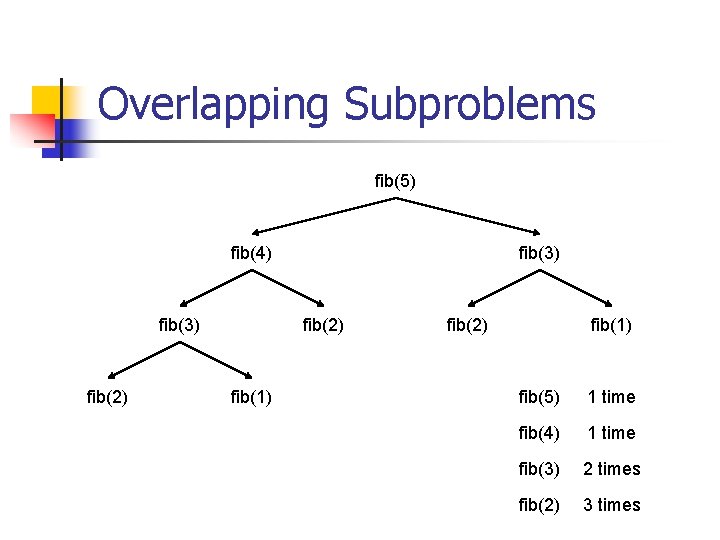
Overlapping Subproblems fib(5) fib(4) fib(3) fib(2) fib(1) fib(5) 1 time fib(4) 1 time fib(3) 2 times fib(2) 3 times

Bottom-Up Computation def fib(n): if n <= 2: return 1 else: return fib(n - 1) + fib(n - 2) To find fib(5), first find fib(1). . .

Bottom-Up Computation def fib(n): if n <= 2: return 1 else: return fib(n - 1) + fib(n - 2) n fib(n) 1 1 2 1 3 2 4 3 5 5

Worksheet! n Yay.

Why Recursion? n n n Why not just use for/while loops, instead of recursion? 1. It's good to know that you don't need for/while to program loops. 2. Many problems are easier to solve recursively than with for/while loops.

Merge Sort n If only 1 element: n n Do nothing. Otherwise: n n n Split the list in half. Merge sort each half. Merge the sorted halves.

Forestry n (Demo)

Forestry n n Problem: Identify contiguous green squares on the grid, and change their color. Story: We're determining which trees get burned down if a given tree catches fire.

Related Problems n using the "paint" tool to fill a region n clearing out the 0's in Minesweeper

Forest Fire n Let's Code!

Solving Recursively n n Key Idea: Change color of current location. Then recursively burn the 4 neighboring trees. Base Case: location is outside grid, or not green

The Code def burn(grid, row, col): if isvalid(grid, row, col): if getcolor(grid, row, col) == "green": setcolor(grid, row, col, "red") burn(grid, row - 1, col) burn(grid, row, col - 1) burn(grid, row, col + 1) burn(grid, row + 1, col)

Big Ideas n n n Comp Sci focuses on how to compute. Computation involves chugging along from state to state. Rewrite rules tell us what state to go to next. Recursive functions are defined in terms of themselves. Useful recursive functions have a base case(s) and a recursive case(s).