Lecture 15 Recursion Recursion l A recursive function

Lecture 15 Recursion

Recursion l A recursive function is a function that calls itself either directly, or indirectly through another function; it is an alternative to iteration l A recursive solution is generally less efficient in terms of system overhead, due to the overhead of extra function calls; however recursive functions – – l allow us to think of solutions to problems that may be recursive in nature allow us to work with data structures that are best accessed recursively A recursive problem Imagine a computer environment that does not support the multiplication operator (*), but it does support addition (+)

Multiplication using the + operator public int multiply (int m, int n) // IN: m and n, values to be multiplied // PRE: m and n are defined and n > 0 // POST: returns m * n // RETURNS: Product of m * n if n is positive; otherwise, returns m { if (n <= 1) return m; else return m + multiply (m, n - 1); }

Tracing the code l l Trace: In order to display multiply(6(m), 4(n)), we need to know and therefore call – 6 + multiply (6, 3) – in order to calculate this result we need to know and therefore call l 6 + multiply (6, 2) l in order to calculate this result we need to know – 6 + multiply (6, 1) l we know the result of multiply (6, 1) l because n = 1, 6 is returned to the calling function – 6 + 6 (returned) = 12 and is returned to the calling function l 6 + 12 (returned) = 18 and is returned to the calling function – 6 + 18 (returned) = 24 and is returned to the calling function in main() 24 is displayed notice the multiply() function was called 5 times

Algorithm of Recursive Functions l The recursive functions we will work with will generally consist of an if statement with the form shown below if the stopping case is reached // if (n <= 1) solve the problem // return m else reduce the problem using recursion // return m + multiply(m, n - 1 ) l Problems that lend themselves to recursive solution have the following characteristics – one or more simple cases of the problem (stopping cases) have a straightforward, non-recursive solution – For the other cases, there is a process (using recursion) for substituting one or more reduced cases of the problem closer to a stopping case – Eventually the problem can be reduced to stopping cases only

Factorial = 6! l A factorial is a number n such that n = n * (n-1) * (n - 2) * (n - 3) … (n - 2)) * ( n - (n -1)) * 1 or n = n * factorial(n - 1) l 6 factorial 6! = 6 * 5 * 4 * 3 * 2 * 1 l or recursively 6! = 6 * 5! -> 5 * 4! -> 4 * 3! -> 3 * 2! -> 2*1 stopping case) 1! = 1 by definition (the

int Factorial(int n) int Factorial (int n) // IN: n, value to find the factorial of // PRE: n is defined and n > 0 // POST: returns n! // RETURNS: Factorial of n is positive; otherwise, returns 1 { if (n <= 1) return 1; else return n * Factorial (n - 1); }

Head Recursion If the recursive call happens at the beginning of the code, then we have a case of head recursion Eg: public void foo(int n){ if (n>0) foo(n-1); System. out. println(n); }

Tail Recursion If the recursive call happens at the end of the code, then we have a case of tail recursion Eg: public void foo(int n){ if (n>0) System. out. println(n); foo(n-1); } Equivalent to running a loop Exercise: convert the code to an iterative loop

Tower of Hanoi Problem l l l Suppose we have 3 pegs named A, B and C We have 3 disks named (1 -largest, 2 -next, 3 smallest) in peg A. How do we move 3 pegs from A to C using B? – – l We can only move one disk at a time We cannot place a larger disk on the top of a smaller one Now how do we generalize this algorithm? B C A

A Recursive Algorithm l If you have one disk, then the problem is solved – l l If you have 2 disks how would you solve the problem? If you have n disks (n > 1) , then divide and conquer – – – l Move disk from source to destination Move (n-1) disks from source to intermediate Move one disk from source to destination Move (n-1) disks from intermediate to destination This gives us a very elegant solution

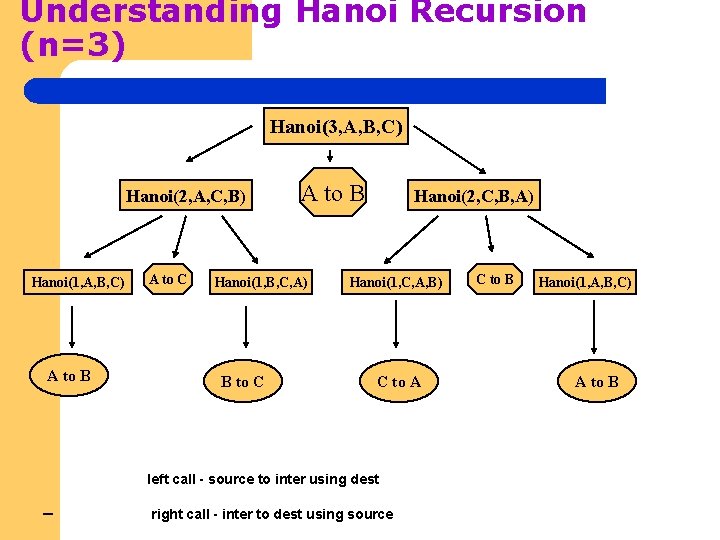
Tower of Hanoi Code // TOWER OF HANOI ALGORITHM public void hanoi(int n, char source, char dest, char inter) { if (n==1) System. out. println("move disk ” + n + " from “ +source+" to “+dest) ; else { hanoi(n-1, source, inter, dest); System. out. println (“move disk ”+ n + " from “+source+" to “+dest) ; hanoi(n-1, inter, dest, source); } l A=source, B=destination, C=intermediate B C A

Understanding Hanoi Recursion (n=3) Hanoi(3, A, B, C) Hanoi(2, A, C, B) Hanoi(1, A, B, C) A to B A to C A to B Hanoi(1, B, C, A) B to C Hanoi(2, C, B, A) Hanoi(1, C, A, B) C to A left call - source to inter using dest – right call - inter to dest using source C to B Hanoi(1, A, B, C) A to B