Recursion Chapter 7 Recursion Chapter Objectives To understand

Recursion Chapter 7: Recursion

Chapter Objectives • • To understand how to think recursively To learn how to trace a recursive method Show recursion is used in math formulas To learn how to write recursive algorithms and methods for searching arrays • To learn about recursive data structures and recursive methods for a Linked. List class • To understand how to use recursion to solve the Towers of Hanoi problem Chapter 7: Recursion 2

Chapter Objectives (continued) • To understand how to use recursion to process twodimensional images • To learn how to apply backtracking to solve search problems such as finding a path through a maze Chapter 7: Recursion 3

Recursive Thinking • Recursion is a problem-solving approach that can be used to generate simple solutions to certain kinds of problems that would be difficult to solve in other ways • Recursion splits a problem into one or more simpler versions of itself Chapter 7: Recursion 4

Recursive Thinking Chapter 7: Recursion 5

Recursive Algorithm • A given problem is a candidate for recursive solution if you can define a base case and a recursive case • Base case: There is at least one case, for a small value of n, that can be solved directly • Recursive case: A problem of a given size n can be split into one or more smaller versions of the same problem Chapter 7: Recursion 6

Steps to Design a Recursive Algorithm • Recognize the base case and provide a solution to it • Devise a strategy to • Split the problem into smaller versions of itself • Smaller versions must progress toward base case • Then to solve the original problem… • …combine the solutions of the smaller (or smallest) problems in such a way as to solve the problem Chapter 7: Recursion 7

Recursive Algorithm to Search Array • Given: Array of n elements, sorted in increasing order • Replace problem of searching n elements by problem of searching n/2 elements • To find target element… • Look at element in the middle • If middle element equals target, then done • Else if target is less than middle element • Repeat search on first half • Else (target is greater than middle element) • Repeat search on second half Chapter 7: Recursion 8

Recursive Algorithm to Search Array • Suppose we search for “ 7” in this array of 25 elements: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 8 9, 97 • Middle element is 41 • Since 7 is less than 41, repeat search using 1 st half: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 • Middle element is 13 • Since 7 is less then 13, repeat using 1 st half: 2, 3, 5, 7, 11 • Middle element is 5 • Chapter 7: Recursion 9

Recursive Algorithm to Search Array • If array is empty • Return -1 • Else if middle element matches target • Return subscript of element • Else if target is less than middle element • Recursively search first half of array • Else • Recursively search second half of array Chapter 7: Recursion 10

General Recursive algorithm • If the problem can be solved for current value of n • Solve it (base case) • Else • Recursively apply the algorithm to one or more problems with smaller value(s) of n (recursive case) Chapter 7: Recursion 11

Steps to Design Recursive Algorithm • In general… • A base case (small n) that can be solved directly • Problem of size n can be split into smaller version(s) of the same problem (recursive case) • To design a recursive algorithm, we must • Recognize base case, and provide solution to it • Devise a strategy to split problem into smaller versions of itself • Combine solutions to smaller problems so that large problem is solved correctly Chapter 7: Recursion 12

Recursive String Length Algorithm • How to find length of a string? • Lots of ways to do this • How about a recursive solution? • Length of empty string is 0 • Length of non-empty string is length of first character plus length of the “rest of the string” • That is, 1 + length of rest of the string • For example, length of “abcd” is 1 + length of “bcd” • And so on… Chapter 7: Recursion 13

Recursive String Length Algorithm Chapter 7: Recursion 14

Recursive String Length Algorithm • In Java public static int length(String str) { if (str == null || str. equals("")) return 0; else return 1 + length(str. substring(1)); } Chapter 7: Recursion 15

Run-Time Stack and Activation Frames • “Activation frame” pushed onto run-time stack • Run-time stack is like “scratch paper” • OS can save information (keep state) • For later use Chapter 7: Recursion 16

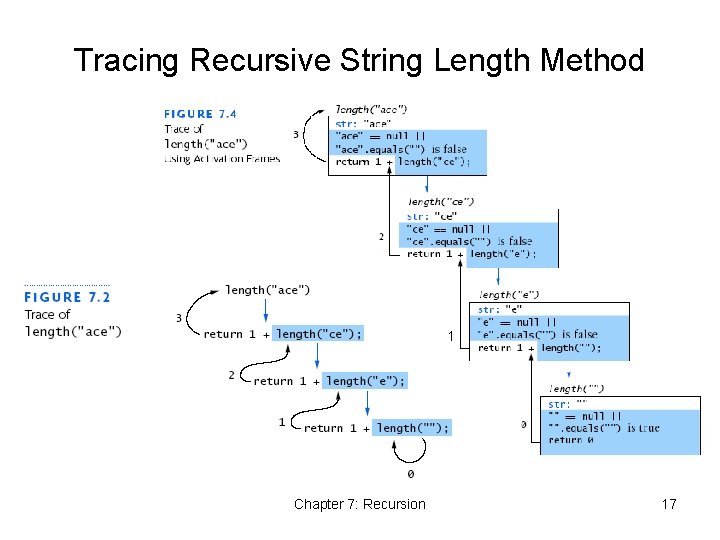
Tracing Recursive String Length Method 1 Chapter 7: Recursion 17

Proving that a Recursive Method is Correct • Proof by induction • Prove theorem is true for the base case • Show that if theorem is assumed true for n, then it must be true for n+1 • Proof of recursion is similar to induction • Verify that the base case is solved correctly • Verify that each recursive case progresses towards the base case • Verify that if all smaller problems are solved correctly, then the original problem is also solved correctly Chapter 7: Recursion 18

Prove Recursive String Length is Correct • Base case? • Empty string is of length 0 • Recursive case makes progress towards base case? • String gets smaller by 1 each time • Show that if smaller problem solved correctly, then original problem is solved correctly • Smaller problem: length(str. substring(1)) • If small problem correct, then length of original string is correct: 1 + length(str. substring(1)) Chapter 7: Recursion 19

Recursive Math Formulas • Mathematics has many naturally recursive formulas • Examples include: • Factorial • Powers • Greatest common divisor • Note that if recursive problem is too big, a stack overflow error will occur • Space available for run-time stack is limited Chapter 7: Recursion 20

Factorial • How do you pronounce “n!” ? • As you know, n! = n (n-1) (n-2) … 1 • And 0! = 1 • Recursive definition? • We have: n! = n (n-1)! • Can easily write a recursive method for factorial… Chapter 7: Recursion 21

Recursive Factorial Method Chapter 7: Recursion 22

Exponentiation • If n is a non-negative integer, xn is x times itself, n times • And x 0 = 1 • For example, 27 = 2 2 = 128 • Recursive definition? • We have: xn = x xn-1 • Can easily write recursive method… Chapter 7: Recursion 23

Recursive Exponentiation Method Chapter 7: Recursion 24

Recursion Versus Iteration • What is iteration? • A loop repetition condition determines whether to repeat the loop body or exit from the loop • In recursion, the condition tests for a base case • There are similarities between recursion and iteration • You can always write an iterative solution to a problem that is solvable by recursion • You are probably more familiar with iteration • So, why bother with recursion? • Recursive code often simpler than an iterative algorithm and thus easier to write, read, and debug Chapter 7: Recursion 25

Tail Recursion • “Tail recursion” or “last-line recursion” • Single recursive call, and it is last line of the method • All of the examples we have considered so far are examples of tail recursion • Easy to convert tail recursive method to iterative method • Example on the next slide… Chapter 7: Recursion 26

Iterative Factorial Method Chapter 7: Recursion 27

Efficiency of Recursion • Is recursion more or less efficient than iteration? • Recursive methods often slower than iteration: Why? • The overhead for loop repetition is smaller than the overhead for a method call and return • Recall, run-time stack • If it is easier to conceptualize an algorithm using recursion, then you should code it as a recursive method • The reduction in efficiency does not outweigh the advantage of readable code that is easy to debug Chapter 7: Recursion 28

Fibonacci Numbers • Fibonacci numbers developed to model rabbit population • Defined as fib 1 = 1, fib 2 = 1, fibn = fibn-1 + fibn-2 • The first several Fibonacci numbers are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, … • Easy to write a recursive method for Fibonacci numbers • See next slide… Chapter 7: Recursion 29

Inefficient Recursive Fibonacci Method Chapter 7: Recursion 30

Inefficient Recursive Fibonacci Method • Why is the obvious Fibonacci recursion inefficient? • Consider fibonacci(7) • Compute fibonacci(6) and fibonacci(5) • Then fibonacci(5), fibonacci(4) fibonacci(3) • Then fibonacci(4), fibonacci(3), fibonacci(2), fibonacci(1) • And so on… • Why is this inefficient? Chapter 7: Recursion 31

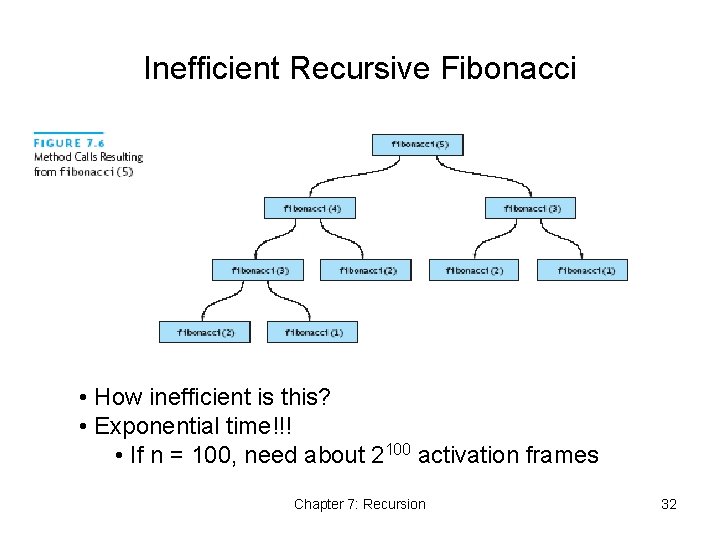
Inefficient Recursive Fibonacci • How inefficient is this? • Exponential time!!! • If n = 100, need about 2100 activation frames Chapter 7: Recursion 32

Efficient Recursive Fibonacci Method • An O(n) Fibonacci algorithm… • If we know current and previous Fibonacci numbers • Then next Fibonacci number is current + previous • Method fibo • 1 st argument is current Fibonacci (fib. Current) • 2 nd argument is previous Fibonacci (fib. Previous) • 3 rd argument is n • When n = 1, base case, so return fib. Current • Otherwise, return fibo(fib. Current + fib. Previous, fib. Current, n - 1) • Start by computing: fibo(1, 0, n) Chapter 7: Recursion 33

Efficient Recursive Fibonacci Method Chapter 7: Recursion 34

Efficient Recursive Fibonacci Method How efficient? Chapter 7: Recursion 35

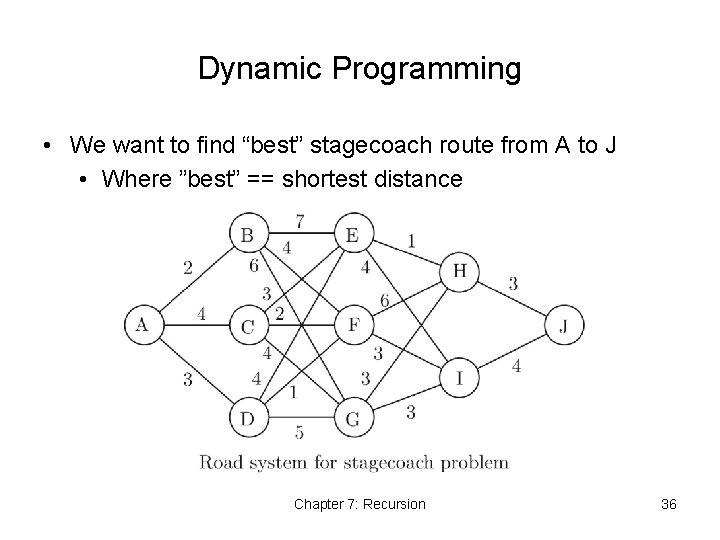
Dynamic Programming • We want to find “best” stagecoach route from A to J • Where ”best” == shortest distance Chapter 7: Recursion 36

Dynamic Programming • Let F(X) be shortest distance from A to X • Note that, for example, F(J) = min{F(H) + 3, F(I) + 4} • This provides a recursive method to find F(J)… Chapter 7: Recursion 37

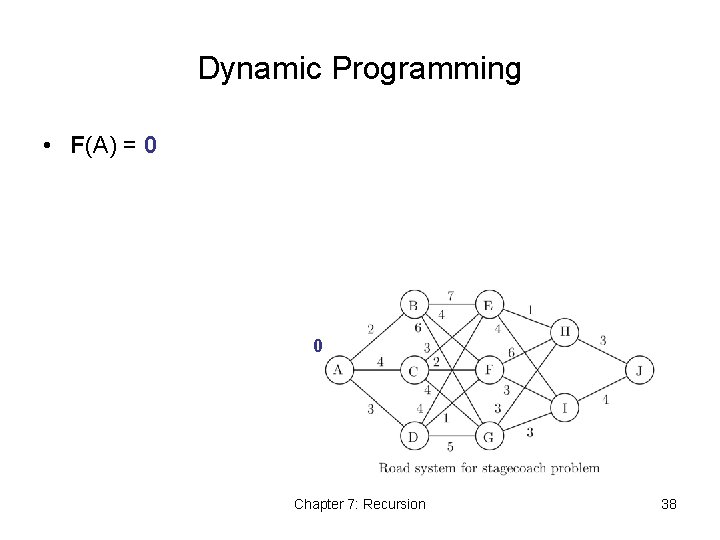
Dynamic Programming • F(A) = 0 0 Chapter 7: Recursion 38

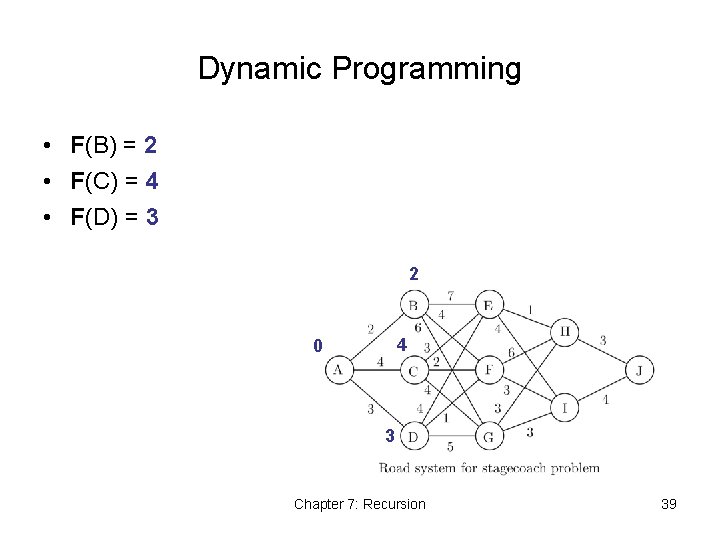
Dynamic Programming • F(B) = 2 • F(C) = 4 • F(D) = 3 2 4 0 3 Chapter 7: Recursion 39

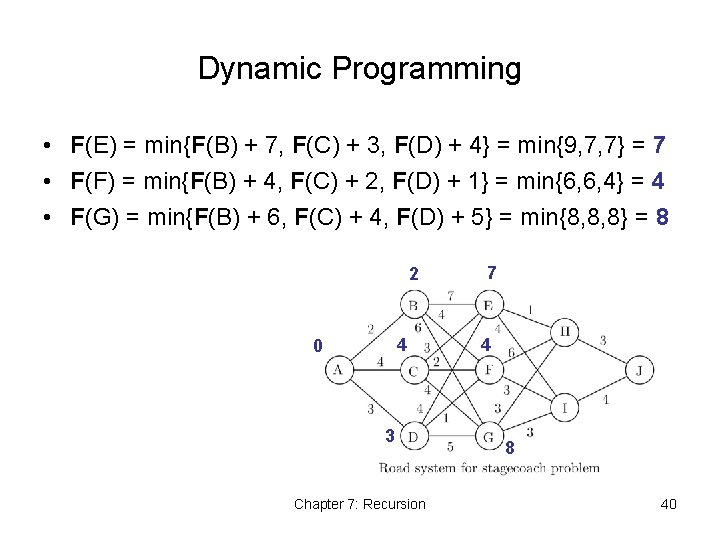
Dynamic Programming • F(E) = min{F(B) + 7, F(C) + 3, F(D) + 4} = min{9, 7, 7} = 7 • F(F) = min{F(B) + 4, F(C) + 2, F(D) + 1} = min{6, 6, 4} = 4 • F(G) = min{F(B) + 6, F(C) + 4, F(D) + 5} = min{8, 8, 8} = 8 2 4 0 3 Chapter 7: Recursion 7 4 8 40

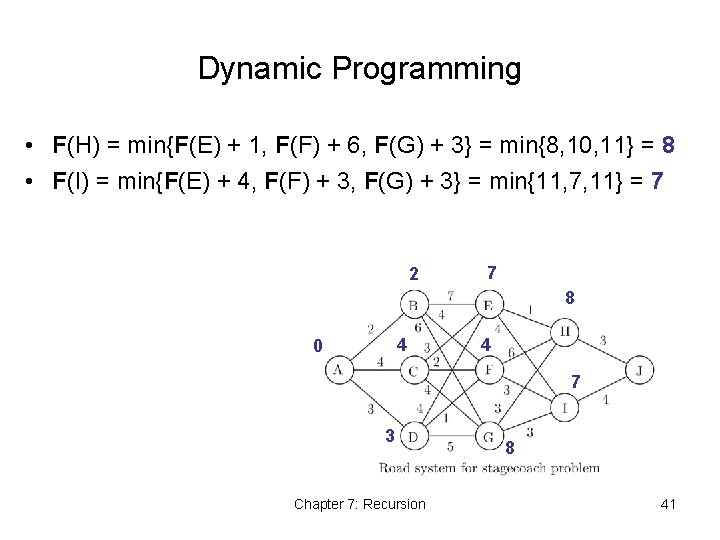
Dynamic Programming • F(H) = min{F(E) + 1, F(F) + 6, F(G) + 3} = min{8, 10, 11} = 8 • F(I) = min{F(E) + 4, F(F) + 3, F(G) + 3} = min{11, 7, 11} = 7 2 7 8 4 0 4 7 3 Chapter 7: Recursion 8 41

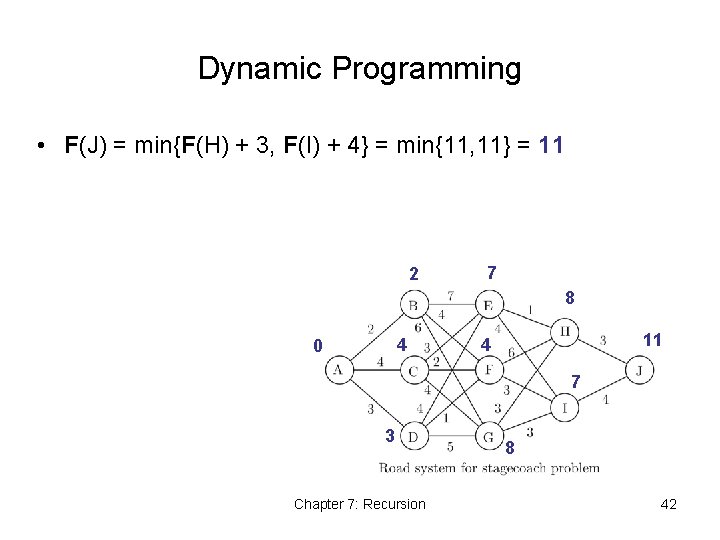
Dynamic Programming • F(J) = min{F(H) + 3, F(I) + 4} = min{11, 11} = 11 2 7 8 4 0 11 4 7 3 Chapter 7: Recursion 8 42

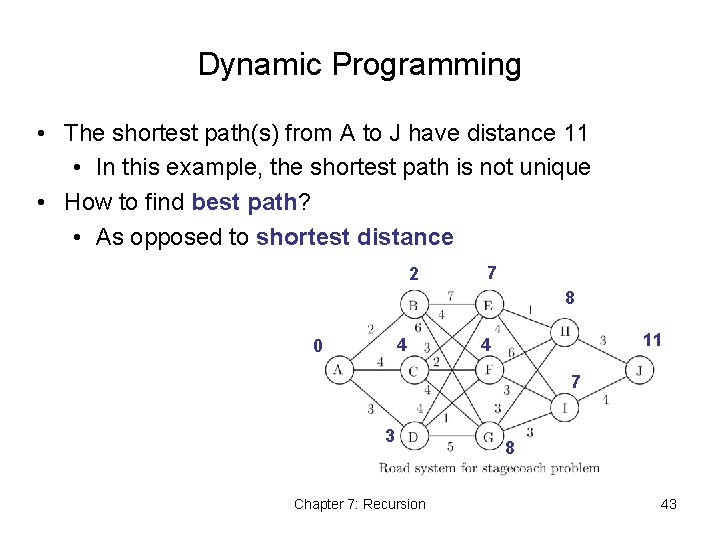
Dynamic Programming • The shortest path(s) from A to J have distance 11 • In this example, the shortest path is not unique • How to find best path? • As opposed to shortest distance 2 7 8 4 0 11 4 7 3 Chapter 7: Recursion 8 43

Recursive Array Search • Searching an array can be accomplished using recursion • Simplest way to search is a linear search • Examine one element at a time starting with the first element and ending with the last • Base case for recursive search is an empty array • Result is negative one • Another base case would be when the array element being examined matches the target • Recursive step is to search the rest of the array, excluding the element just examined Chapter 7: Recursion 44

Algorithm for Recursive Linear Array Search Chapter 7: Recursion 45

Implementation of Recursive Linear Search Chapter 7: Recursion 46

Design of a Binary Search Algorithm • Binary search can be performed only on an array that has been sorted • We assume array is in increasing order • Stop cases • The array is empty • Element being examined matches the target • Check the middle element for a match with the target • Throw away the half of the array • Throw away the half that the target cannot be in Chapter 7: Recursion 47

Binary Search Algorithm Chapter 7: Recursion 48

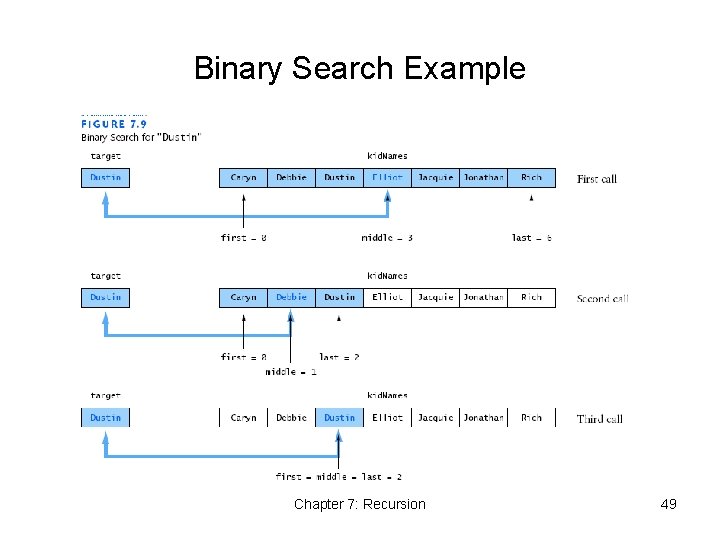
Binary Search Example Chapter 7: Recursion 49

Implementation of Binary Search Chapter 7: Recursion 50

Implementation of Binary Search Chapter 7: Recursion 51

Efficiency of Binary Search • At each recursive call we eliminate half the array elements from consideration • O(log 2 n) Chapter 7: Recursion 52

Comparable Interface • Classes that implement the Comparable interface must define a compare. To method that enables its objects to be compared in a standard way • Compare. To allows you to define ordering of elements Chapter 7: Recursion 53

Method Arrays. binary. Search • Java API class Arrays contains a binary. Search method • Can be called with sorted arrays of primitive types or with sorted arrays of objects • If the objects in the array are not mutually comparable or if the array is not sorted, the results are undefined • If there are multiple copies of the target value in the array, there is no guarantee which one will be found • Throws Class. Cast. Exception if the target is not comparable to the array elements Chapter 7: Recursion 54

Recursive Data Structures • Computer scientists often encounter data structures that are defined recursively • Trees (Chapter 8) are defined recursively • Linked list can be described as a recursive data structure • Recursive methods useful for processing recursive data structures • The first language developed for artificial intelligence research was a recursive language called LISP • “LISt Processing” language Chapter 7: Recursion 55

Recursive Definition of a Linked List • A non-empty linked list is a collection of nodes where each node references another linked list consisting of the nodes that follow it in the list • The last node references an empty list • A linked list is empty, or it contains a node, called the list head, that stores data and a reference to a linked list Chapter 7: Recursion 56

Recursive Size Method Chapter 7: Recursion 57

Recursive to. String Method Chapter 7: Recursion 58

Recursive Replace Method Chapter 7: Recursion 59

Recursive Add Method Chapter 7: Recursion 60

Recursive Remove Method Chapter 7: Recursion 61

Recursive Remove Method Chapter 7: Recursion 62

Problem Solving with Recursion • Will look at two problems • Towers of Hanoi • Counting cells in a blob Chapter 7: Recursion 63

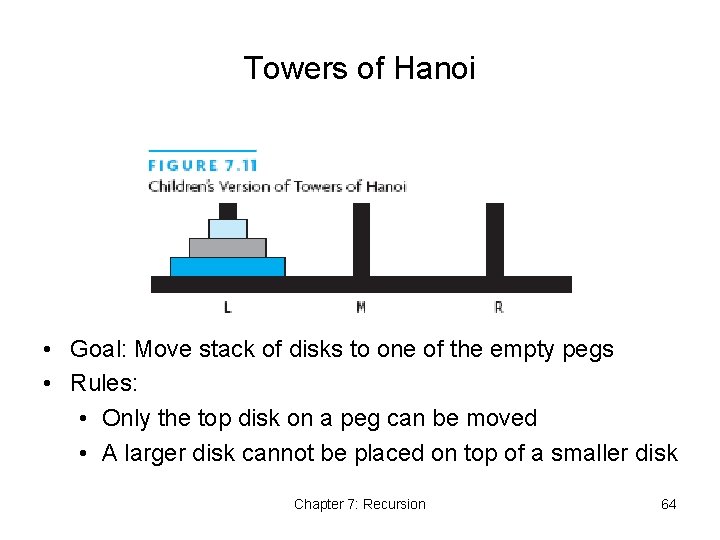
Towers of Hanoi • Goal: Move stack of disks to one of the empty pegs • Rules: • Only the top disk on a peg can be moved • A larger disk cannot be placed on top of a smaller disk Chapter 7: Recursion 64

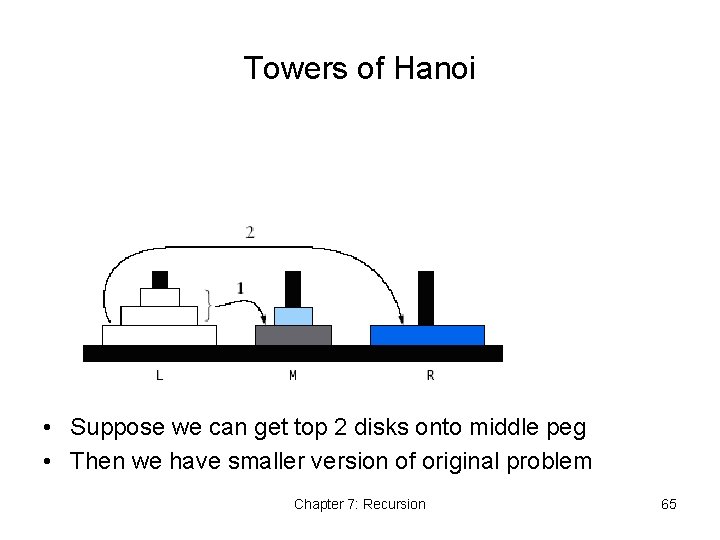
Towers of Hanoi • Suppose we can get top 2 disks onto middle peg • Then we have smaller version of original problem Chapter 7: Recursion 65

Towers of Hanoi Chapter 7: Recursion 66

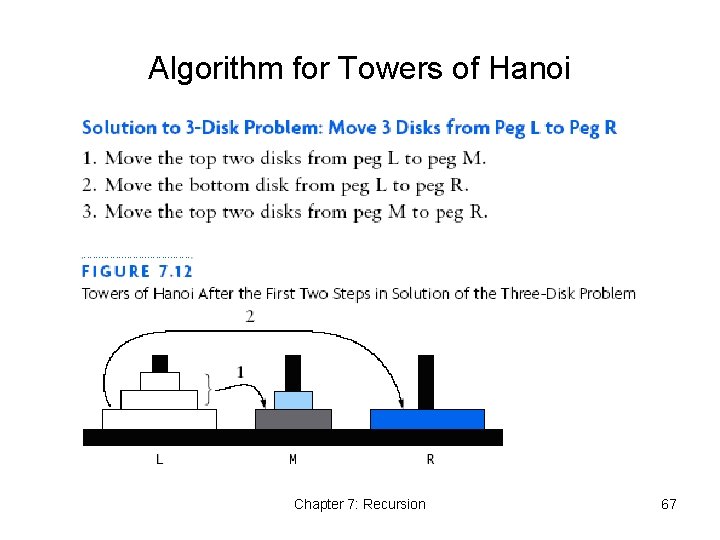
Algorithm for Towers of Hanoi Chapter 7: Recursion 67

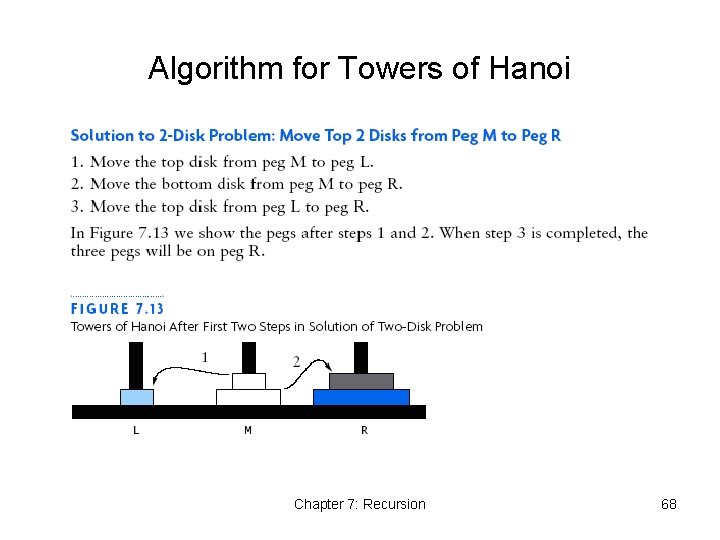
Algorithm for Towers of Hanoi Chapter 7: Recursion 68

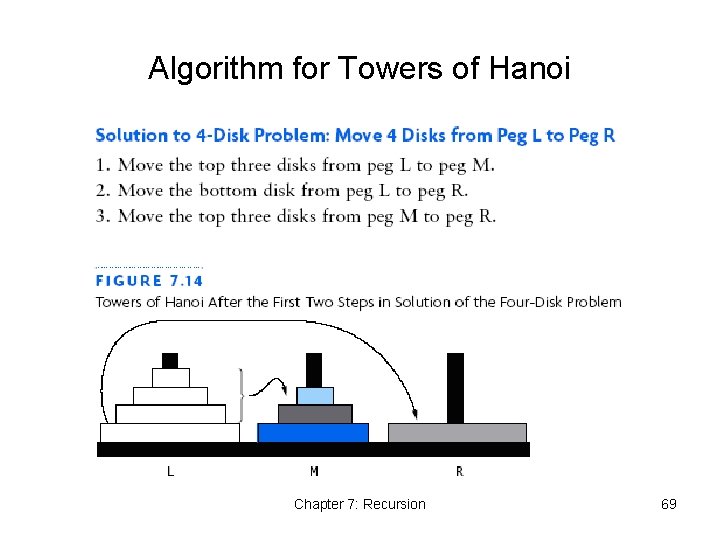
Algorithm for Towers of Hanoi Chapter 7: Recursion 69

Recursive Algorithm for Towers of Hanoi Chapter 7: Recursion 70

Recursive Towers of Hanoi Chapter 7: Recursion 71

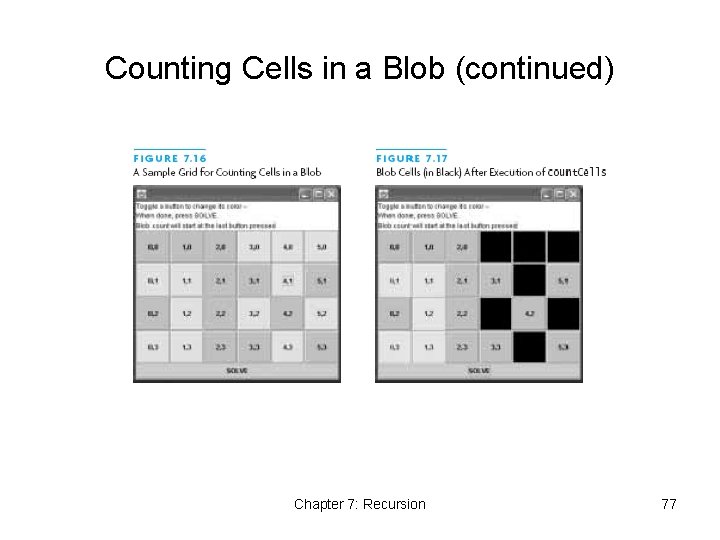
Counting Cells in a Blob • Consider how we might process an image that is presented as a two-dimensional array of color values • Information in the image may come from • X-Ray • MRI • Satellite imagery • Etc. • Goal is to determine the size of any area in the image that is considered abnormal because of its color values Chapter 7: Recursion 72

Counting Cells in a Blob (continued) Chapter 7: Recursion 73

Counting Cells in a Blob (continued) Chapter 7: Recursion 74

Implementation Chapter 7: Recursion 75

Implementation (continued) Chapter 7: Recursion 76

Counting Cells in a Blob (continued) Chapter 7: Recursion 77

Backtracking • Backtracking is an approach to implementing systematic trial and error in a search for a solution • An example is finding a path through a maze • If you are attempting to walk through a maze, you will probably walk down a path as far as you can go • Eventually, you will reach your destination or you won’t be able to go any farther • If you can’t go any farther, you will need to retrace your steps • Backtracking is a systematic approach to trying alternative paths and eliminating them if they don’t work Chapter 7: Recursion 78

Backtracking • Never try the exact same path more than once, and you will eventually find a solution path if one exists • Problems that are solved by backtracking can be described as a set of choices made by some method • Recursion allows us to implement backtracking in a relatively straightforward manner • Each activation frame is used to remember the choice that was made at that particular decision point • A program that plays chess may involve some kind of backtracking algorithm Chapter 7: Recursion 79

Backtracking Chapter 7: Recursion 80

Recursive Algorithm for Finding Maze Path Chapter 7: Recursion 81

Maze Path Implementation Chapter 7: Recursion 82

Maze Path Implementation Chapter 7: Recursion 83

Maze Path Implementation Chapter 7: Recursion 84

Recursion Java Code • http: //www. cs. sjsu. edu/~stamp/CS 46 B/other/recursion/ Chapter 7: Recursion 85

Chapter Review • A recursive method has a standard form • To prove that a recursive algorithm is correct, you must • Verify that the base case is recognized and solved correctly • Verify that each recursive case makes progress toward the base case • Verify that if all smaller problems are solved correctly, then the original problem must also be solved correctly • The run-time stack uses activation frames to keep track of argument values and return points during recursive method calls Chapter 7: Recursion 86

Chapter Review • Mathematical Sequences and formulas that are defined recursively can be implemented naturally as recursive methods • Recursive data structures are data structures that have a component that is the same data structure • Towers of Hanoi and counting cells in a blob can both be solved with recursion • Backtracking is a technique that enables you to write programs that can be used to explore different alternative paths in a search for a solution Chapter 7: Recursion 87