Recursion Recursion Slide 2 Recursion Recursion Slide 3

Recursion

Recursion / Slide 2 Recursion *

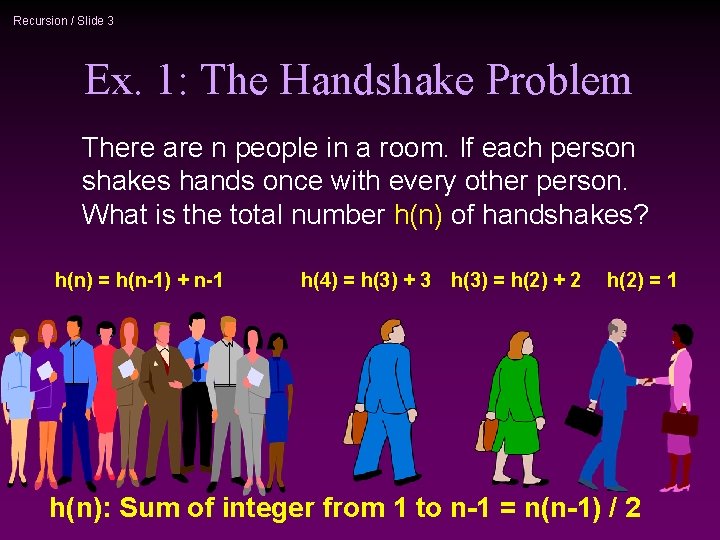
Recursion / Slide 3 Ex. 1: The Handshake Problem There are n people in a room. If each person shakes hands once with every other person. What is the total number h(n) of handshakes? h(n) = h(n-1) + n-1 h(4) = h(3) + 3 h(3) = h(2) + 2 h(2) = 1 h(n): Sum of integer from 1 to n-1 = n(n-1) / 2

Recursion / Slide 4 Recursion * In some problems, it may be natural to define the problem in terms of the problem itself. * Recursion is useful for problems that can be represented by a simpler version of the same problem. * Example: the factorial function 6! = 6 * 5 * 4 * 3 * 2 * 1 We could write: 6! = 6 * 5!

Recursion / Slide 5 Example 2: factorial function In general, we can express the factorial function as follows: n! = n * (n-1)! Is this correct? Well… almost. The factorial function is only defined for positive integers. So we should be a bit more precise: n! = 1 n! = n * (n-1)! (if n is equal to 1) (if n is larger than 1)

Recursion / Slide 6 factorial function int fac(int numb){ if(numb<=1) return 1; else return numb * fac(numb-1); } recursion means that a function calls itself

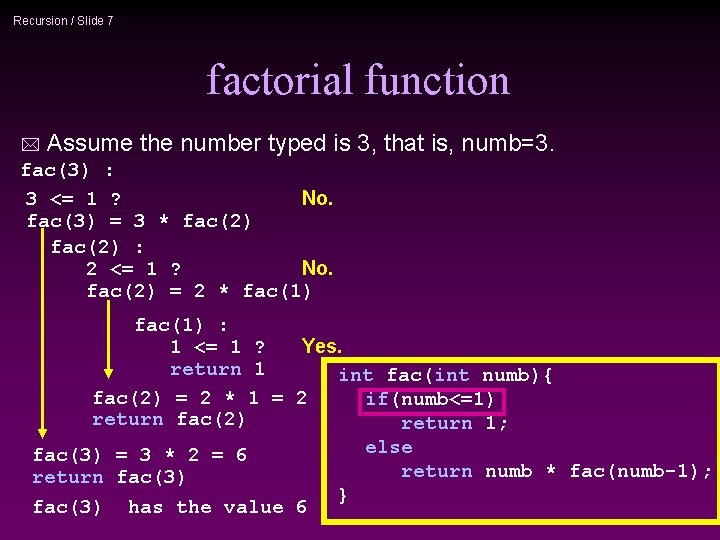
Recursion / Slide 7 factorial function * Assume the number typed is 3, that is, numb=3. fac(3) : 3 <= 1 ? No. fac(3) = 3 * fac(2) : 2 <= 1 ? No. fac(2) = 2 * fac(1) : 1 <= 1 ? Yes. return 1 int fac(int numb){ fac(2) = 2 * 1 = 2 if(numb<=1) return fac(2) return 1; else fac(3) = 3 * 2 = 6 return numb * fac(numb-1); return fac(3) } fac(3) has the value 6

Recursion / Slide 8 factorial function For certain problems (such as the factorial function), a recursive solution often leads to short and elegant code. Compare the recursive solution with the iterative solution: Recursive solution Iterative solution int fac(int numb){ if(numb<=1) int product=1; return 1; while(numb>1){ else product *= numb; return numb*fac(numb-1); numb--; } } return product; }

Recursion / Slide 9 Recursion We must always make sure that the recursion bottoms out: *A recursive function must contain at least one non-recursive branch. * The recursive calls must eventually lead to a non-recursive branch.

Recursion / Slide 10 Example 3: Fibonacci numbers //Calculate Fibonacci numbers using recursive function. //A very inefficient way, but illustrates recursion well int fib(int number) { if (number == 0) return 0; if (number == 1) return 1; return (fib(number-1) + fib(number-2)); }

Recursion / Slide 11

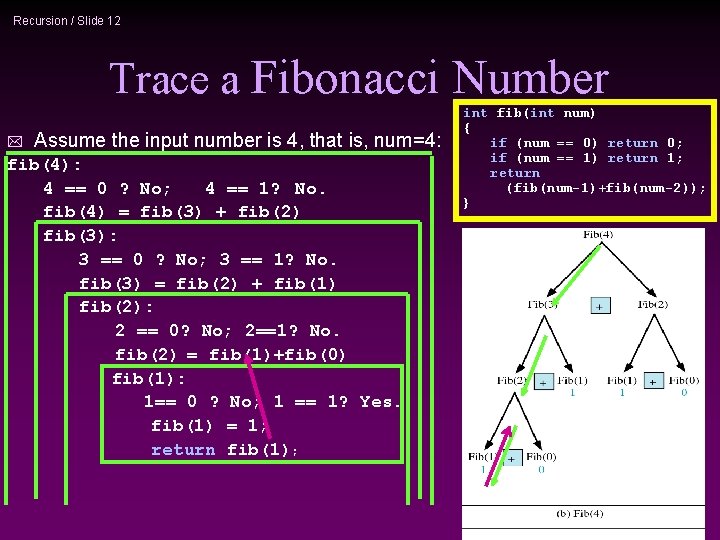
Recursion / Slide 12 Trace a Fibonacci Number * Assume the input number is 4, that is, num=4: fib(4): 4 == 0 ? No; 4 == 1? No. fib(4) = fib(3) + fib(2) fib(3): 3 == 0 ? No; 3 == 1? No. fib(3) = fib(2) + fib(1) fib(2): 2 == 0? No; 2==1? No. fib(2) = fib(1)+fib(0) fib(1): 1== 0 ? No; 1 == 1? Yes. fib(1) = 1; return fib(1); int fib(int num) { if (num == 0) return 0; if (num == 1) return 1; return (fib(num-1)+fib(num-2)); }

Recursion / Slide 13 Trace a Fibonacci Number fib(0): 0 == 0 ? Yes. fib(0) = 0; return fib(0); fib(2) = 1 + 0 = 1; return fib(2); fib(3) = 1 + fib(1): 1 == 0 ? No; 1 == 1? Yes fib(1) = 1; return fib(1); fib(3) = 1 + 1 = 2; return fib(3)

Recursion / Slide 14 Trace a Fibonacci Number fib(2): 2 == 0 ? No; 2 == 1? No. fib(2) = fib(1) + fib(0) fib(1): 1== 0 ? No; 1 == 1? Yes. fib(1) = 1; return fib(1); fib(0): 0 == 0 ? Yes. fib(0) = 0; return fib(0); fib(2) = 1 + 0 = 1; return fib(2); fib(4) = fib(3) + fib(2) = 2 + 1 = 3; return fib(4);

Recursion / Slide 15 Example 4: Fibonacci number w/o recursion //Calculate Fibonacci numbers iteratively //much more efficient than recursive solution int fib(int n) { int f[100]; f[0] = 0; f[1] = 1; for (int i=2; i<= n; i++) f[i] = f[i-1] + f[i-2]; return f[n]; }

Recursion / Slide 16 Example 3: Fibonacci numbers

Recursion / Slide 17 Recursion General Form * How to write recursively? int recur_fn(parameters){ if(stopping condition) return stopping value; // other stopping conditions if needed return function of recur_fn(revised parameters) }

Recursion / Slide 19 Recursive Solution

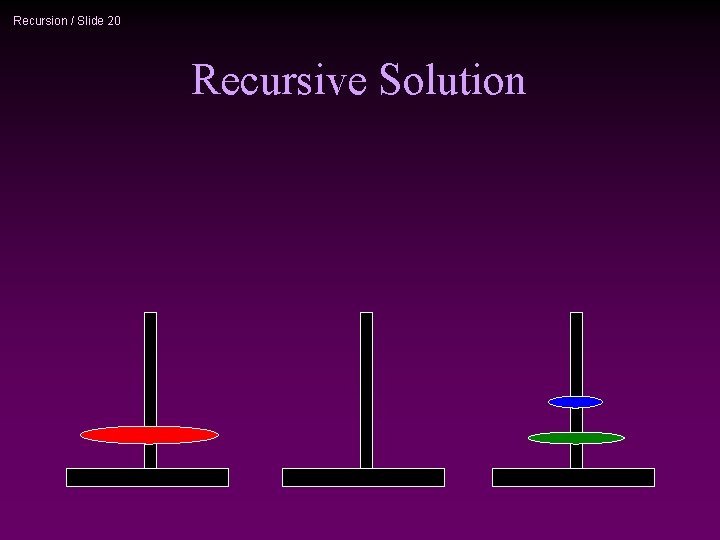
Recursion / Slide 20 Recursive Solution

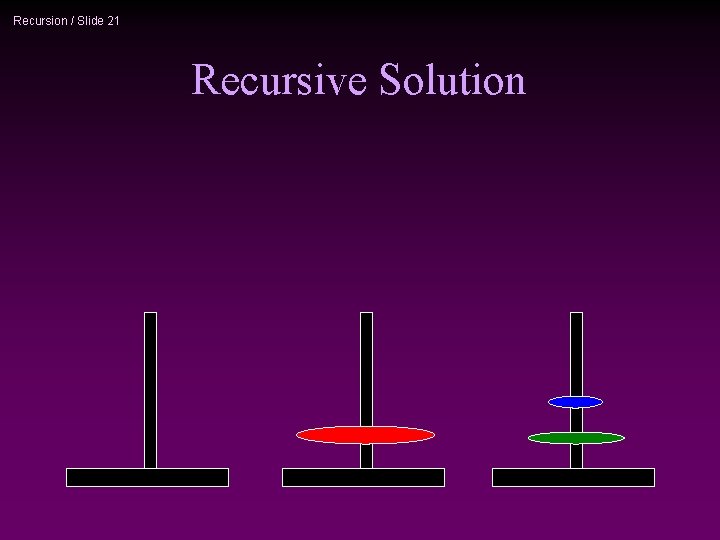
Recursion / Slide 21 Recursive Solution

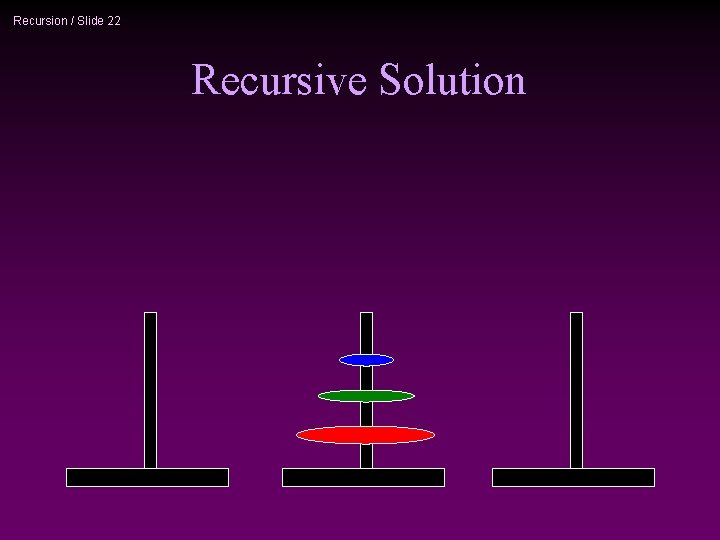
Recursion / Slide 22 Recursive Solution

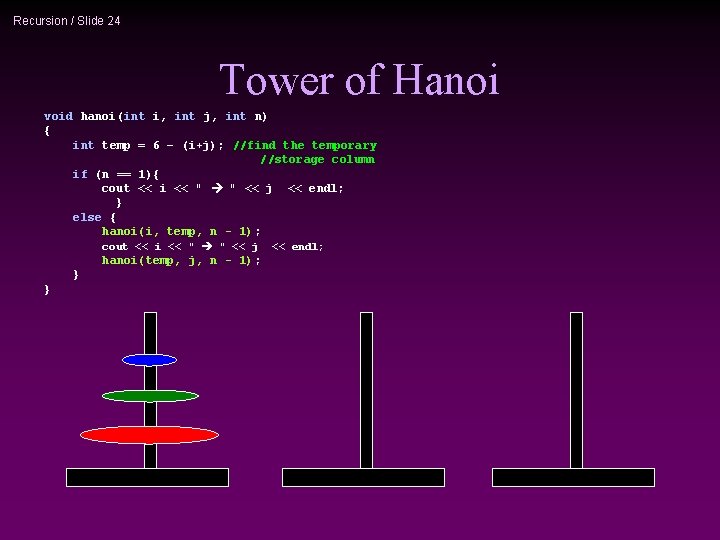
Recursion / Slide 23 Towers of Hanoi i+j+temp =1+2+3= 6 => temp =6 -(i+j) void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

Recursion / Slide 24 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

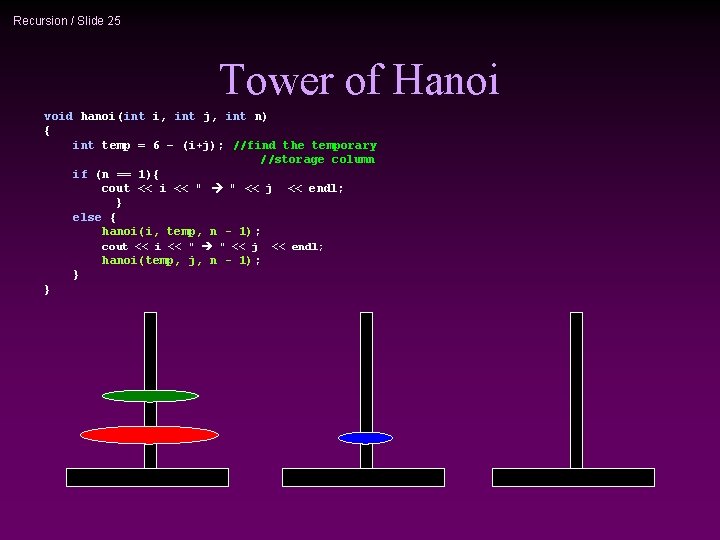
Recursion / Slide 25 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

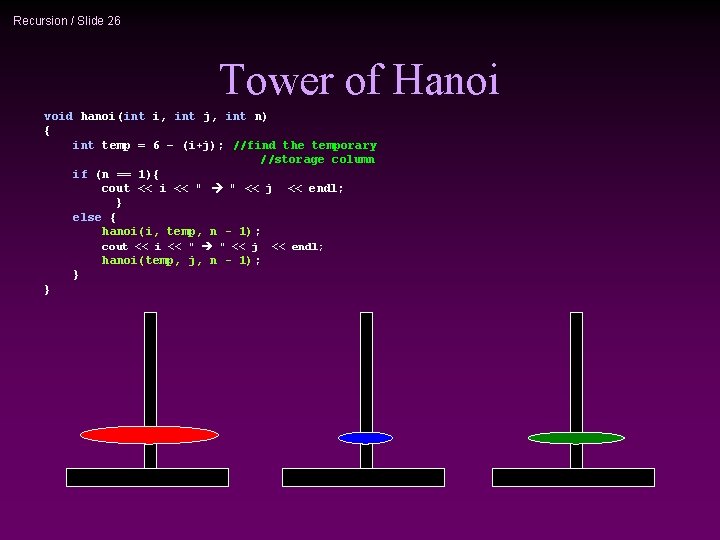
Recursion / Slide 26 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

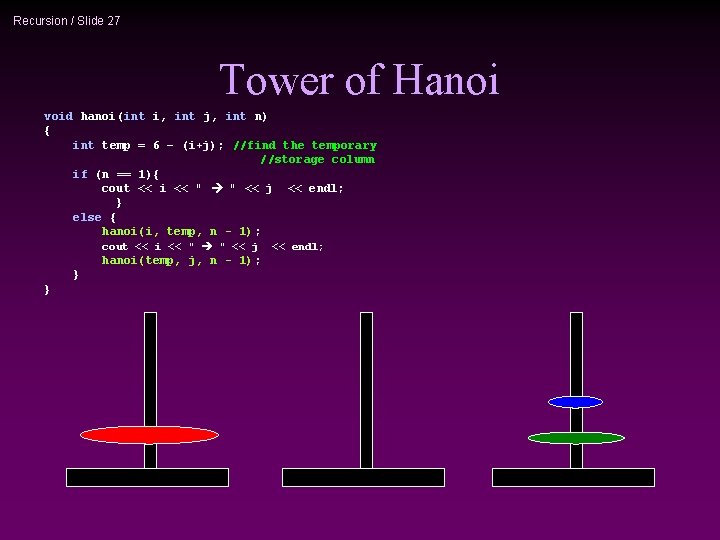
Recursion / Slide 27 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

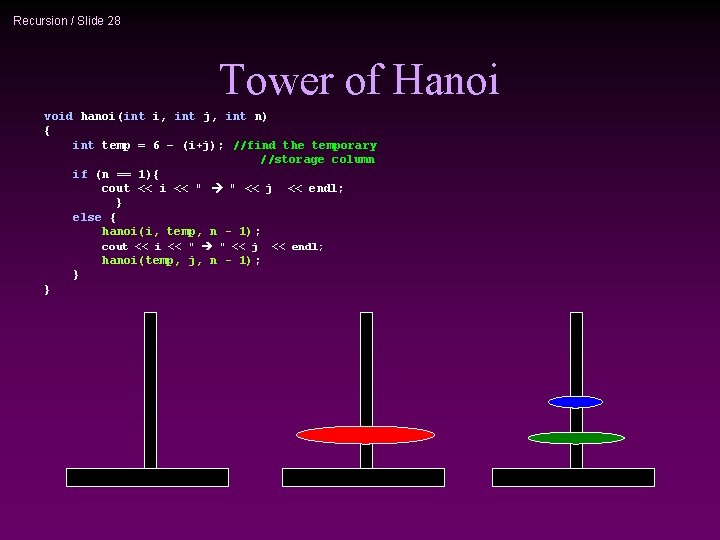
Recursion / Slide 28 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

Recursion / Slide 29 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

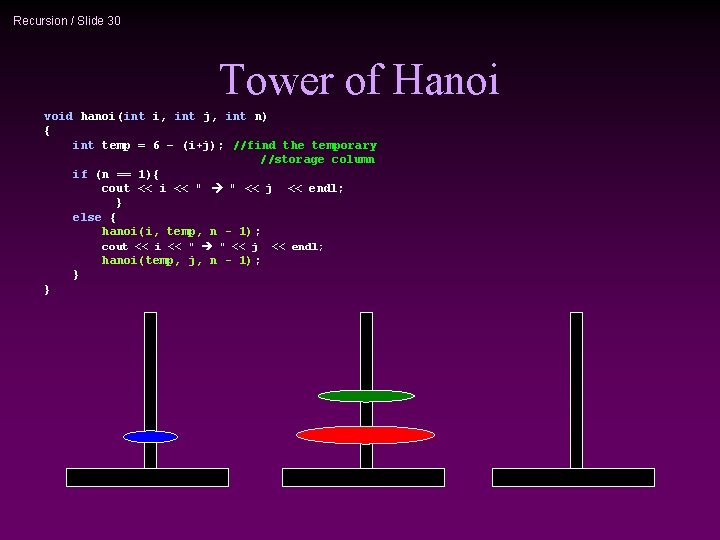
Recursion / Slide 30 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

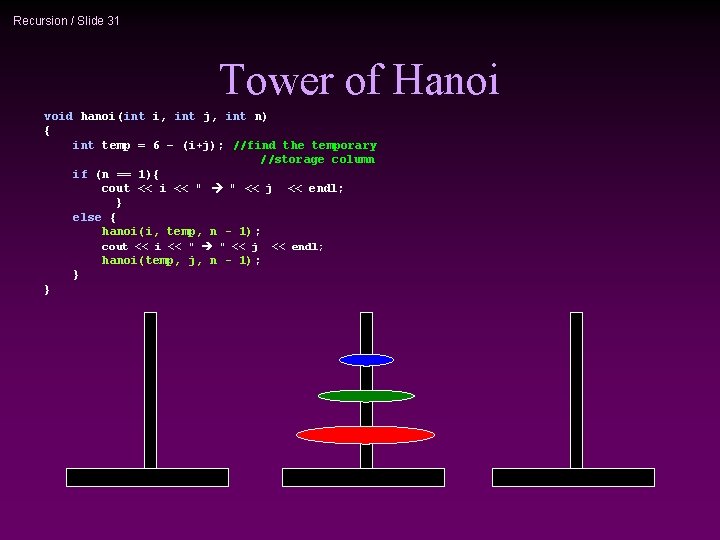
Recursion / Slide 31 Tower of Hanoi void hanoi(int i, int j, int n) { int temp = 6 – (i+j); //find the temporary //storage column if (n == 1){ cout << i << " " << j << endl; } else { hanoi(i, temp, n - 1); cout << i << " " << j hanoi(temp, j, n - 1); } } << endl;

Recursion / Slide 38 Solving Recursive Functions *

Recursion / Slide 39 Solving Recursive Functions *

Recursion / Slide 40 Solving Recursive Functions *

Recursion / Slide 41 Solving Recursive Functions *

Recursion / Slide 42 Solving Recursive Functions *

Recursion / Slide 43 Solving Recursive Functions * ﺩﻭ ﻣﺘﻤﺎیﺰ ﻫﺴﺘﻨﺪ ﺩﻭﺑﻪ

Recursion / Slide 45 Solving Recursive Functions * ﺩﻭ ﻣﺘﻤﺎیﺰ ﻫﺴﺘﻨﺪ ﺩﻭﺑﻪ Ex: -

Recursion / Slide 47 Solving Recursive Functions ﺩﺭﺧﺖﻫﺎی ﺑﺎﺯگﺸﺘی 4 ﻗﻀیﻪ ﺍﺳﺎﺳی 5 -

Recursion / Slide 50 Recursion-tree method • A recursion tree models the costs (time) of a recursive execution of an algorithm. • The recursion tree method is good for generating guesses for the substitution method. Solve T(n) = T(n/4) + T(n/2) + n 2:

Recursion / Slide 51 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2:

Recursion / Slide 52 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: T(n)

Recursion / Slide 53 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: n 2 T(n/4) T(n/2)

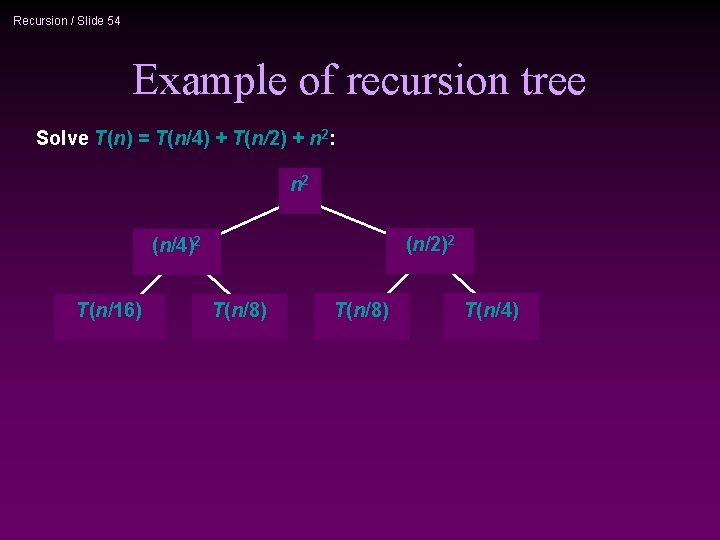
Recursion / Slide 54 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/2)2 (n/4)2 T(n/16) T(n/8) T(n/4)

Recursion / Slide 55 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/2)2 (n/4)2 … (n/16)2 Q(1) (n/8)2 (n/4)2

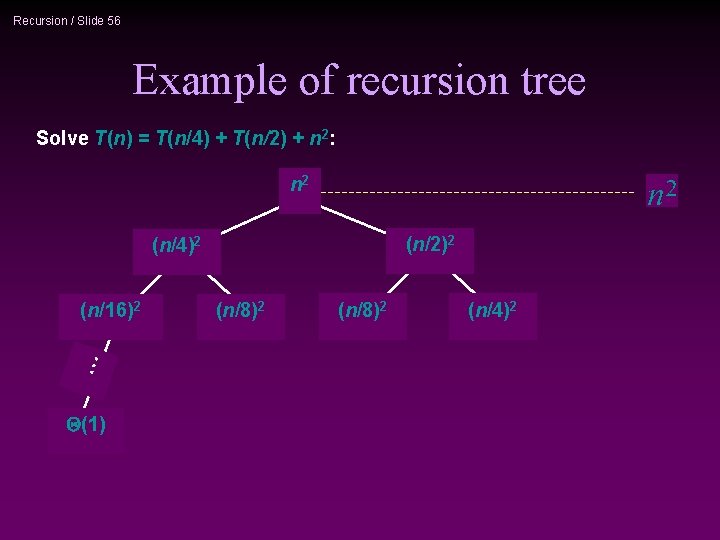
Recursion / Slide 56 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/2)2 (n/4)2 … (n/16)2 Q(1) (n/8)2 (n/4)2

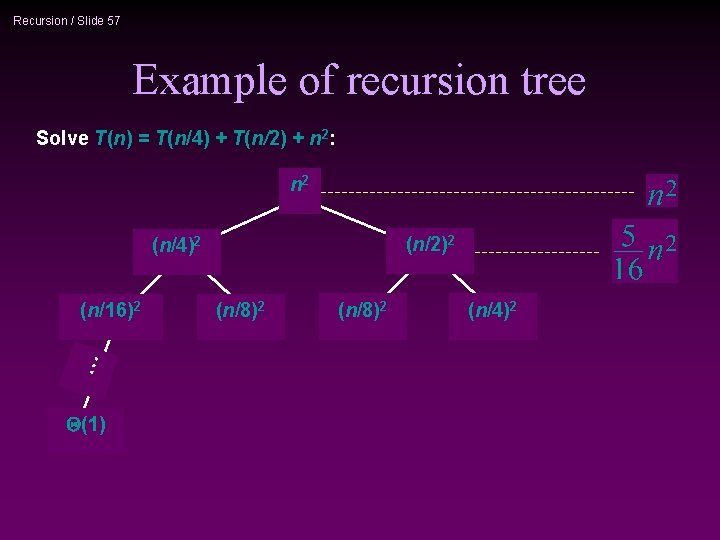
Recursion / Slide 57 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/2)2 (n/4)2 … (n/16)2 Q(1) (n/8)2 (n/4)2

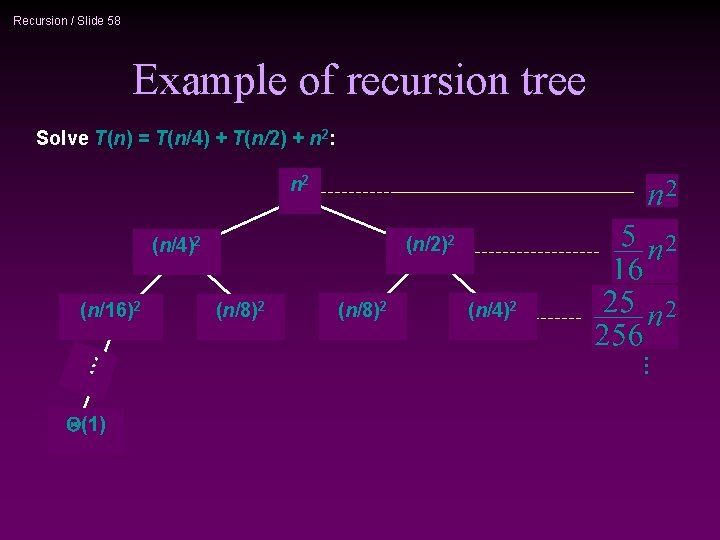
Recursion / Slide 58 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/2)2 … (n/16)2 Q(1) (n/8)2 (n/4)2 … (n/4)2

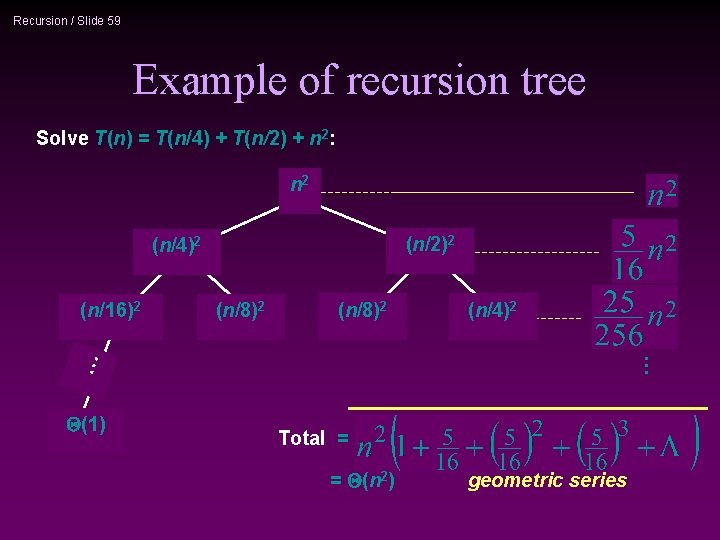
Recursion / Slide 59 Example of recursion tree Solve T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/2)2 (n/4)2 (n/8)2 (n/4)2 … (n/8)2 … (n/16)2 Q(1) Total = = Q(n 2) geometric series

Recursion / Slide 60 Remember: geometric series for x ¹ 1 for |x| < 1

Recursion / Slide 61 The master method applies to recurrences of the form T(n) = a T(n/b) + f (n) , where a ³ 1, b > 1, and f is asymptotically positive.

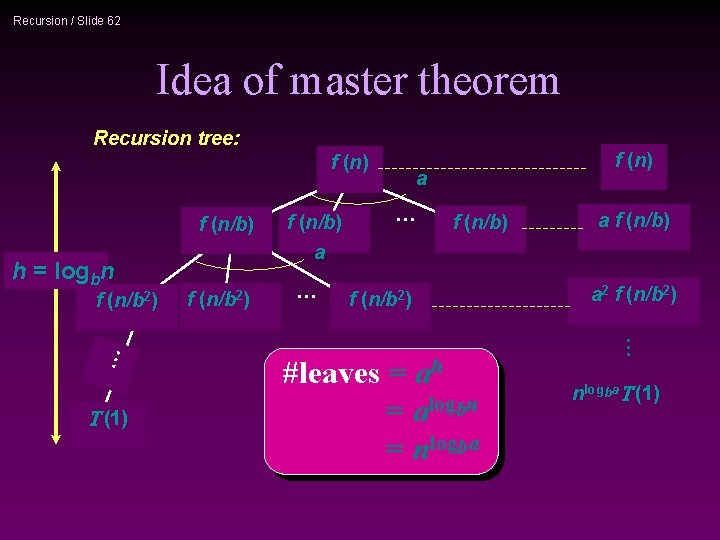
Recursion / Slide 62 Idea of master theorem Recursion tree: f (n/b) h = logbn … f (n/b 2) T (1) f (n/b 2) f (n/b) a … f (n/b) f (n/b 2) #leaves = ah = alogbn = nlogba a f (n/b) a 2 f (n/b 2) … f (n) nlogba. T (1)

Recursion / Slide 63 Three common cases Compare f (n) with nlogba: 1. f (n) = O(nlogba – e) for some constant e > 0. • f (n) grows polynomially slower than nlogba (by an ne factor). Solution: T(n) = Q(nlogba).

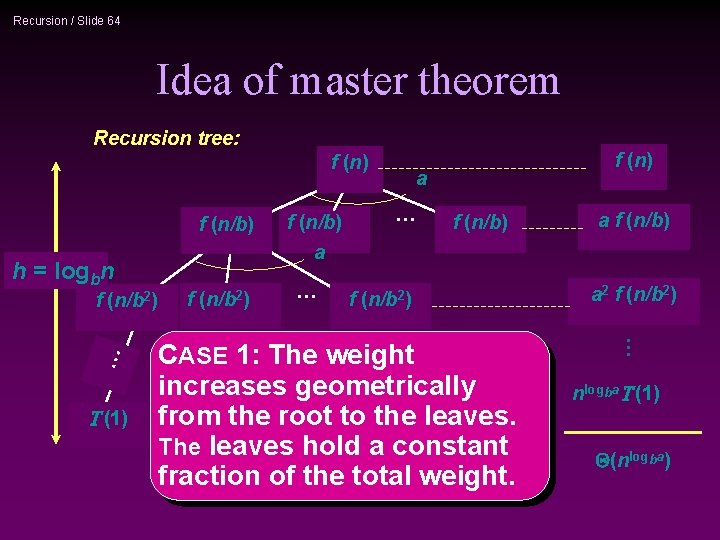
Recursion / Slide 64 Idea of master theorem Recursion tree: f (n/b) h = logbn … f (n/b 2) T (1) f (n/b 2) f (n/b) a … f (n/b) f (n/b 2) CASE 1: The weight increases geometrically from the root to the leaves. The leaves hold a constant fraction of the total weight. a f (n/b) a 2 f (n/b 2) … f (n) nlogba. T (1) Q(nlogba)

Recursion / Slide 65 Three common cases Compare f (n) with nlogba: 2. f (n) = Q(nlogba lgkn) for some constant k ³ 0. • f (n) and nlogba grow at similar rates. Solution: T(n) = Q(nlogba lgk+1 n).

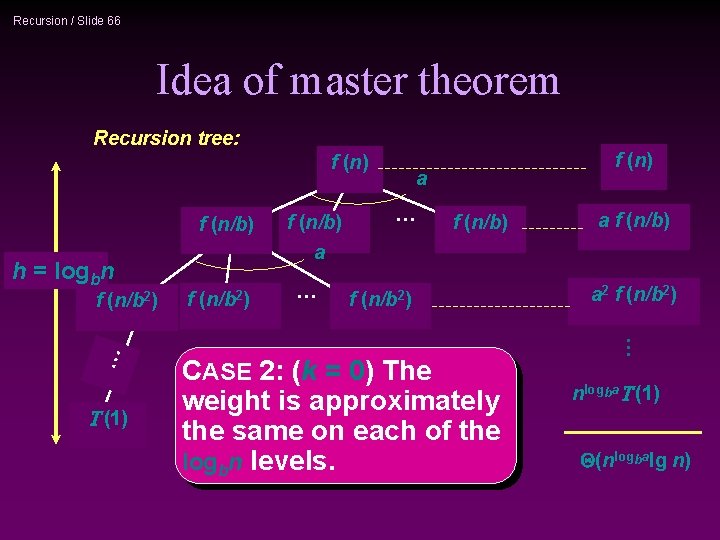
Recursion / Slide 66 Idea of master theorem Recursion tree: f (n/b) … a … f (n/b) f (n/b 2) … h = logbn f (n/b) a f (n) CASE 2: (k = 0) The weight is approximately the same on each of the logbn levels. T (1) f (n/b 2) a f (n/b) a 2 f (n/b 2) … f (n) nlogba. T (1) Q(nlogbalg n)

Recursion / Slide 67 Three common cases (cont. ) Compare f (n) with nlogba: 3. f (n) = W(nlogba + e) for some constant e > 0. • f (n) grows polynomially faster than nlogba (by an ne factor), and f (n) satisfies the regularity condition that a f (n/b) £ c f (n) for some constant c < 1. Solution: T(n) = Q( f (n) ).

Recursion / Slide 68 Idea of master theorem Recursion tree: f (n) f (n/b) h = logbn T (1) f (n/b 2) … a … f (n/b) f (n/b 2) a f (n/b) a 2 f (n/b 2) … … f (n/b 2) f (n/b) a f (n) CASE 3: The weight decreases geometrically from the root to the leaves. The root holds a constant fraction of the total weight. nlogba. T (1) Q( f (n))

Recursion / Slide 69 Examples Ex. T(n) = 4 T(n/2) + n a = 4, b = 2 nlogba = n 2; f (n) = n. CASE 1: f (n) = O(n 2 – e) for e = 1. T(n) = Q(n 2). Ex. T(n) = 4 T(n/2) + n 2 a = 4, b = 2 nlogba = n 2; f (n) = n 2. CASE 2: f (n) = Q(n 2 lg 0 n), that is, k = 0. T(n) = Q(n 2 lg n).

Recursion / Slide 70 Examples Ex. T(n) = 4 T(n/2) + n 3 a = 4, b = 2 nlogba = n 2; f (n) = n 3. CASE 3: f (n) = W(n 2 + e) for e = 1 and 4(cn/2)3 £ cn 3 (reg. cond. ) for c = 1/2. T(n) = Q(n 3). Ex. T(n) = 4 T(n/2) + n 2/lg n a = 4, b = 2 nlogba = n 2; f (n) = n 2/lg n. Master method does not apply. In particular, for every constant e > 0, we have ne = w(lg n).

Recursion / Slide 72 Examples int combin (int n, int k) if (k==0 || k==n) return 1; return combin(n-1, k-1) + combin(n-1, k); ﺗﺎ ﺟﻤﻊ 5 1 ﺗﺎ 6

Recursion / Slide 73 Examples int combin (int n, int k) if (k==0 || k==n) return 1; return combin(n-1, k-1) + combin(n-1, k);

Recursion / Slide 74 Examples int combin (int n, int k) if (k==0 || k==n) return 1; return combin(n-1, k-1) + combin(n-1, k);

Recursion / Slide 75 Examples int combin (int n, int k) if (k==0 || k==n) return 1; return combin(n-1, k-1) + combin(n-1, k);