CHAPITRE II LES SYSTEMES CRISTALLINS 1 ELEMENTS DE

CHAPITRE II LES SYSTEMES CRISTALLINS

1 - ELEMENTS DE SYMETRIE Depuis plus de 150 ans, les cristallographes classent les différents cristaux en relation avec la symétrie de leur forme extérieure. Cette régularité des formes est une conséquence de rôle joué par les éléments de symétrie du cristal. On les divisent en deux catégories: - Les éléments de symétrie d’orientation qui décrivent l’ensemble de la géométrie du polyèdre que constitue le cristal macroscopique. - Les éléments de symétrie de position qui sont relatifs à la structure périodique du cristal microscopique.

1 -1: ELEMENTS D’ORIENTATION Un élément de symétrie d’orientation est un opérateur qui amène un point F à une position d’un point-équivalent B. Il y a 2 catégories d’éléments de symétrie d’orientation: * Opérateurs directes An qui sont des axes de rotation d’un angle a=2 p/n, (n=1, 2, 3, 4, 6). On les symbolise par n. A 1 s’appelle l’identité *Opérateurs inverses n qui font correspondre à un point son image obtenue par inversion par rapport au centre de symétrie C après avoir subie une rotation n. 1 : simple inversion par rapport au centre de symétrie C 2 : réflexion par rapport à un plan, est désignée sous le nom de miroir et symbolisée par m.

1 -2: ELEMENTS DE POSITION Les éléments de position caractérisent les translations de période t. On distingue 2 catégories d’éléments de symétrie de position * Les axes hélicoïdaux: qui combinent une opération de rotation n suivie d’une translation de vecteur t parallèle à l’axe An. * Les plans de glissement: qui commandent une opération de symétrie par rapport à un plan de type m suivie d’une translation t parallèlement à ce plan.

2 -LES 7 SYSTEMES CRISTALLINS L’association des symétries 1, 2, 3, 4, 6, 1, et m conduit à 7 combinaisons possibles donnant 7 systèmes cristallins. Réseau triclinique (a=b=c et a=b=g=90°) Réseau monoclinique (a=b=c et a=g=90° et b=90°) Réseau orthorhombique (a=b=c et a=b=g=90°) Réseau quadratique (a=b=c et a=b=g=90°) Réseau rhomboédrique (a=b=c et a=b= g=90°) Réseau hexagonal (a=b=c , a=b=90° et g=120°) Réseau cubique (a=b=c et a=b=g=90°)

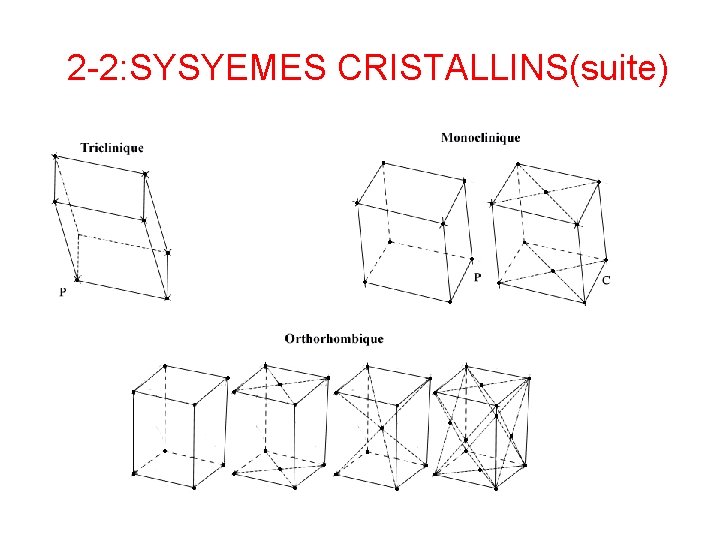
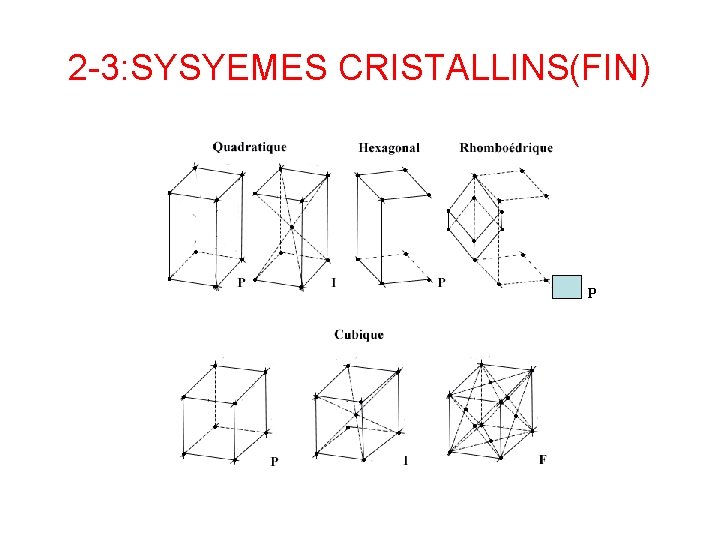
2 -1: SYSTEMES CRISTALLIN (SUITE) Modes de Mailles de Bravais a montré qu’on peut compléter les mailles primitives par des nœuds supplémentaires et obtenir des mailles multiples de même symétrie. Aux 7 mailles primitives P, on associé 7 mailles multiples obtenues en plaçant: - un nœud au centre des bases de la maille : maille C - un nœud au centre du volume de la maille : maille I - un nœud au centre de chaque face de la maille : maille F On peut créer ainsi 7 mailles multiples qui, ajoutées aux 7 mailles primitives constituent les 14 mailles de Bravais.

2 -2: SYSYEMES CRISTALLINS(suite)

2 -3: SYSYEMES CRISTALLINS(FIN) P

3 - EMPILEMENT COMPACT DE SPHÈRES IDENTIQUES. CONVENTIONS Dans le modèle proposé, les atomes (ou les ions) sont considérés comme des sphères identiques, strictement régulières et infiniment dures. Si on veut placer, de façon aussi compacte que possible, des sphères identiques dans un espace à une dimension, il convient de les juxtaposer de telle manière qu'elles se touchent. C'est à dire que si D est la distance entre leurs centres respectifs et R leur rayon alors D = 2 R.

CONVENTIONS (suite 1) Dans l'espace à 2 dimensions, dimensions on place une 3ème sphère tangente à ses deux voisines. Les trois centres définissent un triangle équilatéral. Cette figure est reproduite à l'infini dans son plan. Dans un espace à 3 dimensions, dimensions il faut ensuite placer une couche identique à la précédente dont chaque sphère est tangente à celles de la première couche.

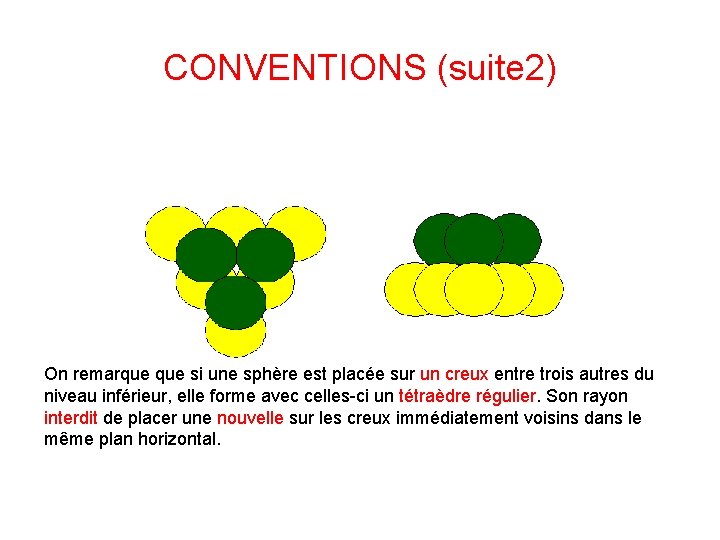
CONVENTIONS (suite 2) On remarque si une sphère est placée sur un creux entre trois autres du niveau inférieur, elle forme avec celles-ci un tétraèdre régulier. Son rayon interdit de placer une nouvelle sur les creux immédiatement voisins dans le même plan horizontal.

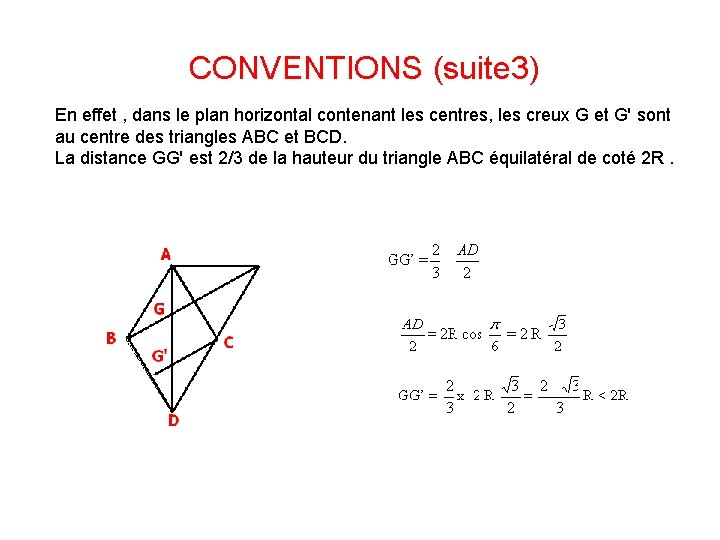
CONVENTIONS (suite 3) En effet , dans le plan horizontal contenant les centres, les creux G et G' sont au centre des triangles ABC et BCD. La distance GG' est 2/3 de la hauteur du triangle ABC équilatéral de coté 2 R.

CONVENTIONS (suite 4) Une difficulté se produit quand il faut placer une troisième couche de sphères. Les creux ne sont pas identiques, car il peuvent être repérés par leur position relative à la première couche (en jaune, dite couche A). Nous allons représenter par des sphères rouges celles de la 2ème couche appelée couche B. Les motifs de la 3ème couche (en jaune aussi) sont à la verticale des sphères de la couche A. On aura un empilement ABAB…

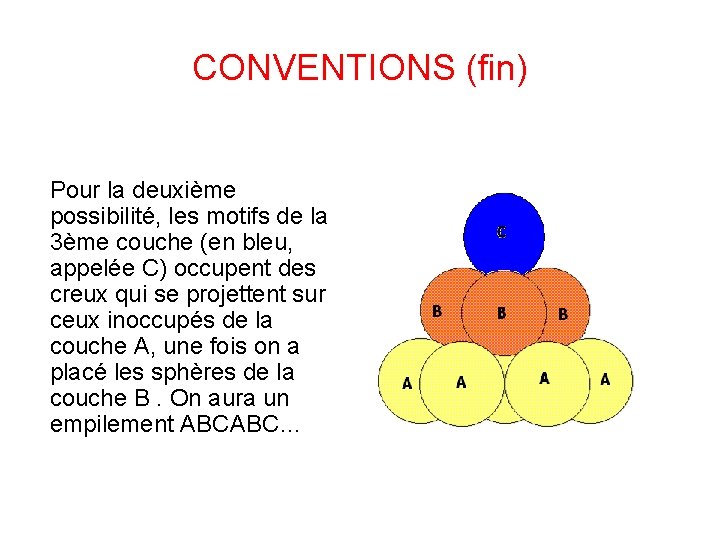
CONVENTIONS (fin) Pour la deuxième possibilité, les motifs de la 3ème couche (en bleu, appelée C) occupent des creux qui se projettent sur ceux inoccupés de la couche A, une fois on a placé les sphères de la couche B. On aura un empilement ABCABC…

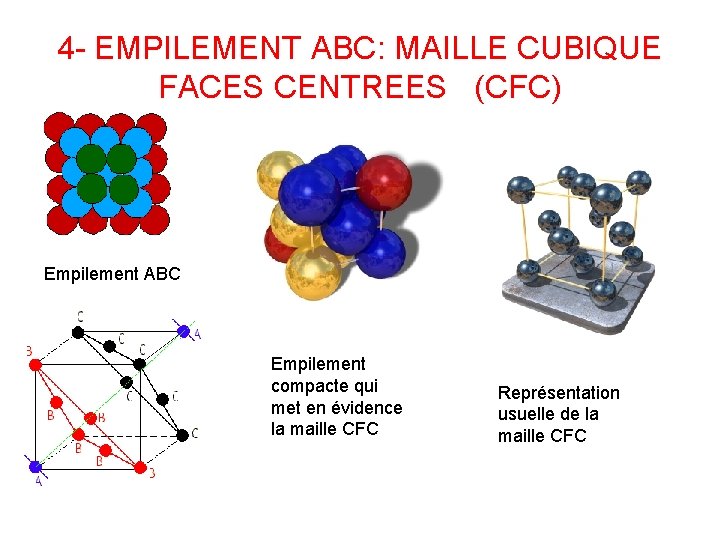
4 - EMPILEMENT ABC: MAILLE CUBIQUE FACES CENTREES (CFC) Empilement ABC Empilement compacte qui met en évidence la maille CFC Représentation usuelle de la maille CFC

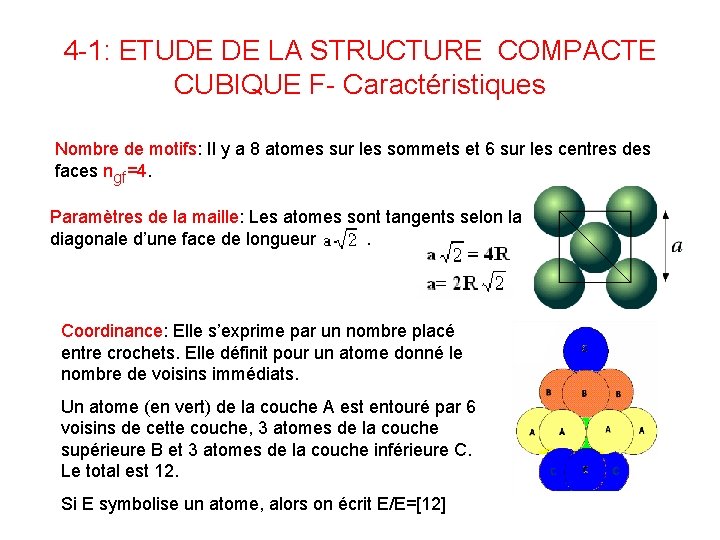
4 -1: ETUDE DE LA STRUCTURE COMPACTE CUBIQUE F- Caractéristiques Nombre de motifs: Il y a 8 atomes sur les sommets et 6 sur les centres des faces ngf=4. Paramètres de la maille: Les atomes sont tangents selon la diagonale d’une face de longueur. Coordinance: Elle s’exprime par un nombre placé entre crochets. Elle définit pour un atome donné le nombre de voisins immédiats. Un atome (en vert) de la couche A est entouré par 6 voisins de cette couche, 3 atomes de la couche supérieure B et 3 atomes de la couche inférieure C. Le total est 12. Si E symbolise un atome, alors on écrit E/E=[12]

ETUDE DE LA STRUCTURE COMPACTE CUBIQUE F- Caractéristiques(suite) Compacité : On la désigne par C et elle est définie par le rapport entre le volume occupé par les atomes à l’intérieur d’une maille et le volume de cette dernière.

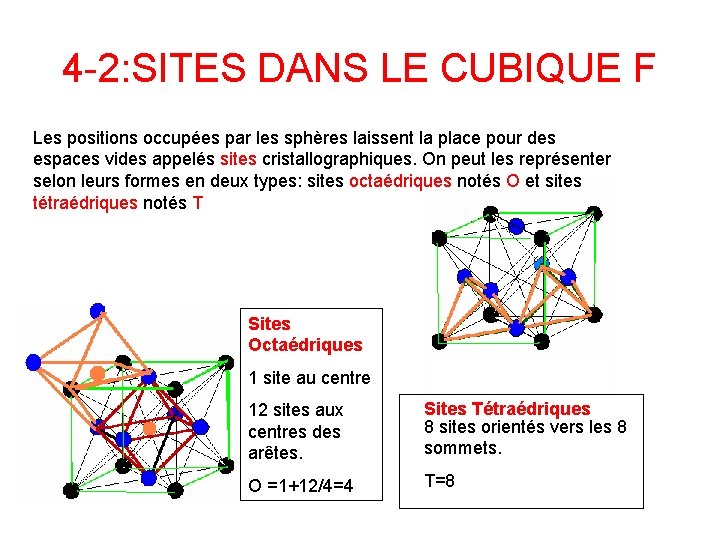
4 -2: SITES DANS LE CUBIQUE F Les positions occupées par les sphères laissent la place pour des espaces vides appelés sites cristallographiques. On peut les représenter selon leurs formes en deux types: sites octaédriques notés O et sites tétraédriques notés T Sites Octaédriques 1 site au centre 12 sites aux centres des arêtes. Sites Tétraédriques 8 sites orientés vers les 8 sommets. O =1+12/4=4 T=8

SITES DANS LE CUBIQUE F(suite) ** Le rayon maximum r. O d’une sphère susceptible de s’insérer dans un site octaédrique est tel que la nouvelle sphère est tangente à 2 sphères de rayon R placées sur 2 sommets d’une arête de longueur a: 2(R+r. O) = a = Ce qui donne r. O = = 0, 414 R ** Le rayon maximum r. T d’une sphère susceptible de s’insérer dans un site tétraédrique est tel que la nouvelle sphère est tangente à la sphère de rayon R d’un sommet et se place au centre du tétraèdre qui est situé à 3/4 de la hauteur relativement sommet. On rappelle que la hauteur représente la distance entre les plans contenant les sphères A et B (ou B et C)/ Elle est égale au 1/3 de la grande diagonale. (R+r. T) = Ce qui donne r. T = = = 0, 225 R

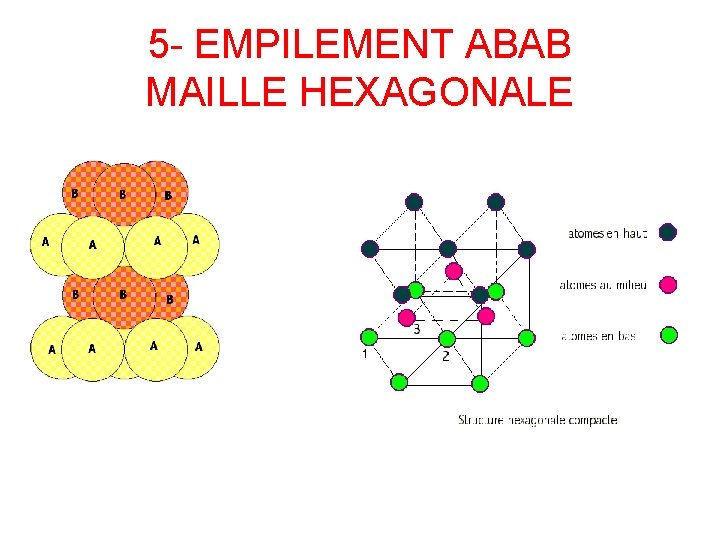
5 - EMPILEMENT ABAB MAILLE HEXAGONALE

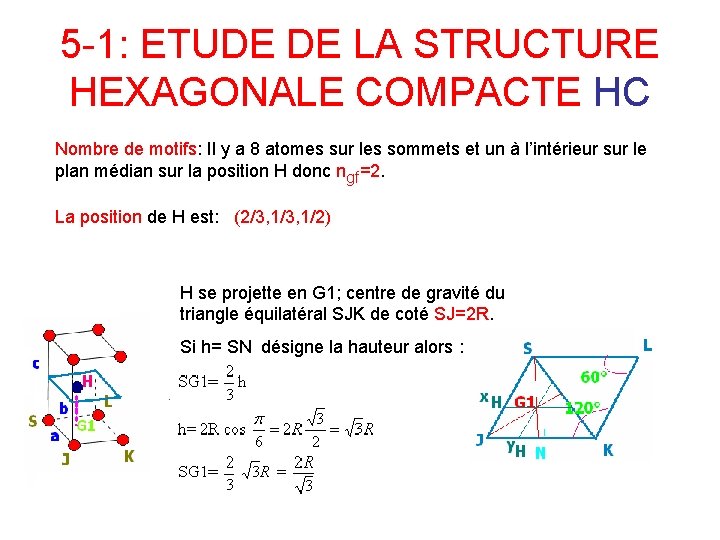
5 -1: ETUDE DE LA STRUCTURE HEXAGONALE COMPACTE HC Nombre de motifs: Il y a 8 atomes sur les sommets et un à l’intérieur sur le plan médian sur la position H donc ngf=2. La position de H est: (2/3, 1/2) H se projette en G 1; centre de gravité du triangle équilatéral SJK de coté SJ=2 R. Si h= SN désigne la hauteur alors :

ETUDE DE LA STRUCTURE HEXAGONALE COMPACTE HC(suite) HJKS est un tétraèdre régulier de coté 2 R. Dans le triangle SG 1 H rectangle en G 1 on a : La maille HC sera caractérisée par deux paramètres : ah=2 R et Ch=2 HG 1 Leur rapport est une constante caractéristique du réseau HC et vaut:

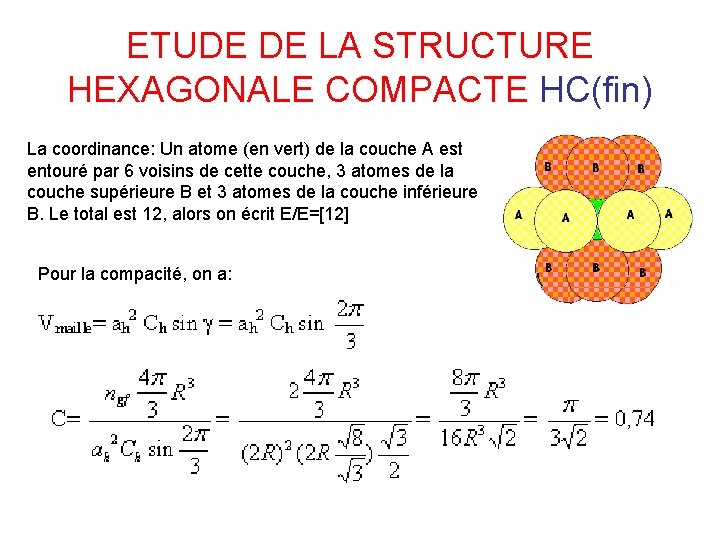
ETUDE DE LA STRUCTURE HEXAGONALE COMPACTE HC(fin) La coordinance: Un atome (en vert) de la couche A est entouré par 6 voisins de cette couche, 3 atomes de la couche supérieure B et 3 atomes de la couche inférieure B. Le total est 12, alors on écrit E/E=[12] Pour la compacité, on a:

5 -2: SITES TETRAEDRIQUES DANS UN EMPILLEMENT COMPACTE HEXAGONAL Les sites tétraédriques sont formés par 2 types différents: * 2 tétraèdres pointant sur l’atome intérieur de la couche B de la maille élémentaire et dont la base est formée par trois atomes d’une base. Ils se situent sur la verticale passant le sommet (Type B) à la distance 1/4 par rapport à la base (Type A). Leurs coordonnées sont (2/3, 1/8 ou 7/8). Il comptent pour 2 par maille.

SITES TETRAEDRIQUES DANS UN EMPILLEMENT COMPACTE HEXAGONAL (Suite) * 8 tétraèdres formés par les 3 atomes voisins de la couche B et pointant chacun vers un sommet de la maille élémentaire. Le site se place sur une arête à la distance 3/4 par rapport à la base; càd aux coordonnées (O ou a, 3/8 ou 5/8). Ils comptent pour 8*1/4 càd 2. Il y a au total 4 sites tétraédriques par maille hexagonale compacte T=4

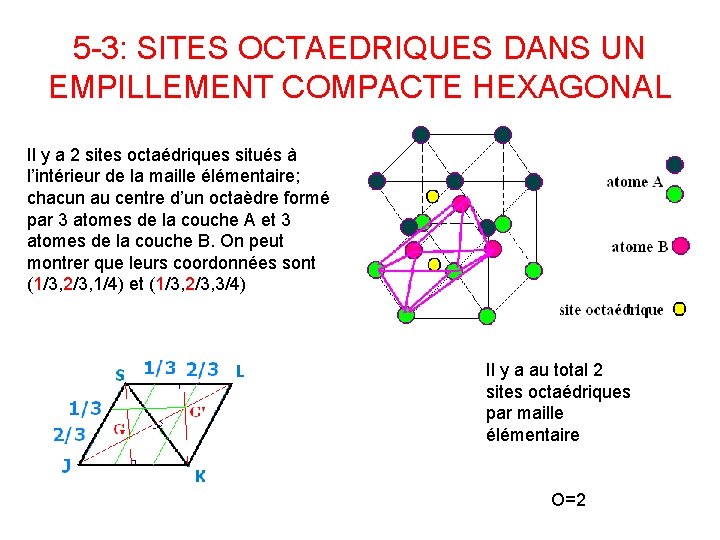
5 -3: SITES OCTAEDRIQUES DANS UN EMPILLEMENT COMPACTE HEXAGONAL Il y a 2 sites octaédriques situés à l’intérieur de la maille élémentaire; chacun au centre d’un octaèdre formé par 3 atomes de la couche A et 3 atomes de la couche B. On peut montrer que leurs coordonnées sont (1/3, 2/3, 1/4) et (1/3, 2/3, 3/4) Il y a au total 2 sites octaédriques par maille élémentaire O=2

PROJECTION COTEE C’est une façon commode de représenter les structures simples en projection sur un plan particulier de la maille. On n’indique la coordonnée réduite de l’atome suivant la direction de projection (la cote), les deux autres sont lues directement sur le plan de la projection. Il est usuel d’indiquer aussi l’origine.