APPUNTI DI GEOMETRIA ANALITICA DELLA RETTA Prima parte

APPUNTI DI GEOMETRIA ANALITICA DELLA RETTA Prima parte

RETTE PARTICOLARI • Rette verticali: hanno equazione • Rette orizzontali: hanno equazione • In particolare: asse Y • In particolare: asse X delle ascisse y=0 delle ordinate x=0 • Rette del semipiano di • Rette del semipiano inferiore: y=k con sinistra: x=k con k<0 (II e III quadrante) k<0 (III e IV quadrante) • Rette del semipiano di • Rette del semipiano destra: x=k con k>0 (I e superiore: y=k con IV quadrante) k>0 (I e II quadrante)

LUNGHEZZA DI SEGMENTI PARTICOLARI • Segmento verticale di estremi • Differenza, in valore assoluto, fra le coordinate che cambiano valore (le ordinate dei due estremi) • Nella formula, poiché i valori assoluti di un argomento o del suo opposto sono uguali… è indifferente l’ordine! • Segmento orizzontale di estremi • Differenza, in valore assoluto, fra le coordinate che cambiano valore (le ascisse dei due estremi) • Nella formula, poiché i valori assoluti di un argomento o del suo opposto sono uguali… è indifferente l’ordine!

RETTE OBLIQUE L’equazione contiene entrambe le variabili in essa: • m è il COEFFICIENTE ANGOLARE e controlla l’inclinazione della retta corrispondente (è definito dal rapporto retta) dove A e B sono due qualunque punti della • q è il TERMINE NOTO e rappresenta l’ordinata del punto in cui la retta corrispondente interseca l’asse delle ordinate (infatti la coppia di valori (0, q) soddisfa l’equazione data)

Se m=0 l’equazione rappresenta una retta orizzontale N. B. non è possibile descrivere rette verticali con questa equazione • Se m<0 l’equazione rappresenta una retta • DECRESCENTE • che forma, con la direzione X positiva UN ANGOLO OTTUSO • Se m>0 l’equazione rappresenta una retta • CRESCENTE • che forma, con la direzione X positiva UN ANGOLO ACUTO

CONDIZIONE DI APPARTENENZA DI UN PUNTO AD UNA RETTA • • • Un punto appartiene ad una retta se le sue coordinate ne soddisfano l’equazione, cioè se, sostituite rispettivamente l’ascissa alla variabile x e l’ordinata alla variabile y, danno luogo ad un’identità (uguaglianza sempre vera) Es: data la retta 2 x-y=4 nel piano, il punto appartiene alla retta, infatti: è un’identità, mentre il punto non le appartiene, per analogo motivo

Trovare l’equazione di una retta passante per un P assegnato e di m assegnato Si deve usare la formula: • Ad es. punto P(-1, 8) e m=-3 la retta ha equazione: y-8=-3(x+1) cioè: y=-3 x+5 • Punto T(0, -6) e m=5 la retta ha equazione: y+6=5(x-0) cioè: y=5 x-6 • Punto S(0, 2) e m=0 la retta ha equazione: • (y-2)=0(x-0) cioè: y=2

• Se q=0 la retta passa per l’origine degli assi cartesiani • Condizione di parallelismo fra rette: • due rette parallele distinte hanno lo stesso coefficiente angolare e diverso termine noto • Due rette parallele coincidenti hanno lo stesso coefficiente angolare e lo stesso termine noto • Condizione di perpendicolarità fra rette: due rette sono perpendicolari se i loro coefficienti angolari sono antireciproci

FASCIO IMPROPRIO • E’ UN INSIEME DI INFINITE RETTE PARALLELE FRA LORO • La caratteristica comune a tali rette è la DIREZIONE quindi il coefficiente angolare • Non vi sono punti in comune fra ogni retta e le altre • L’equazione è: dove è una costante

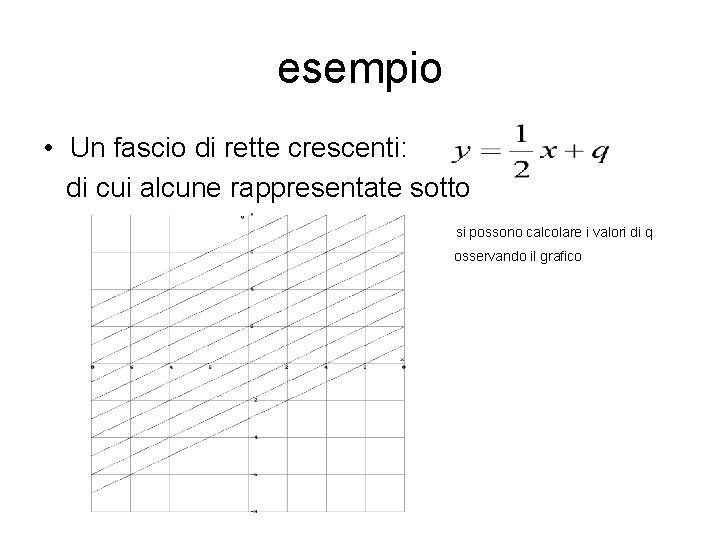
esempio • Un fascio di rette crescenti: di cui alcune rappresentate sotto si possono calcolare i valori di q osservando il grafico

FASCIO PROPRIO • E’ UN INSIEME DI INFINITE RETTE AVENTI UN PUNTO (il centro del fascio) IN COMUNE • La caratteristica comune a tali rette è tale punto, mentre varia la DIREZIONE quindi il coefficiente angolare • L’equazione è: dove è una costante

esempio • Un fascio di rette di centro C(-4, 2): di cui alcune rappresentate sotto si può notare come i valori di q dipendano da m, esplicitando y

Se si tiene l’equazione in forma implicita : ax+by+c=0 a, b, c numeri reali • Se è nullo il coefficiente di y: b=0 => si ottiene l’equazione di una retta verticale • Se è nullo il coefficiente di x: a=0 => si ottiene l’equazione di una retta orizzontale • Se è nullo solo il termine noto c=0 => si ottiene una retta passante per l’origine • Se i tre coefficienti sono diversi da zero => si ottiene una generica retta obliqua non passante per l’origine • N. B. quest’equazione descrive tutti i tipi di rette del piano, al variare del valore dei coefficienti a, b, c

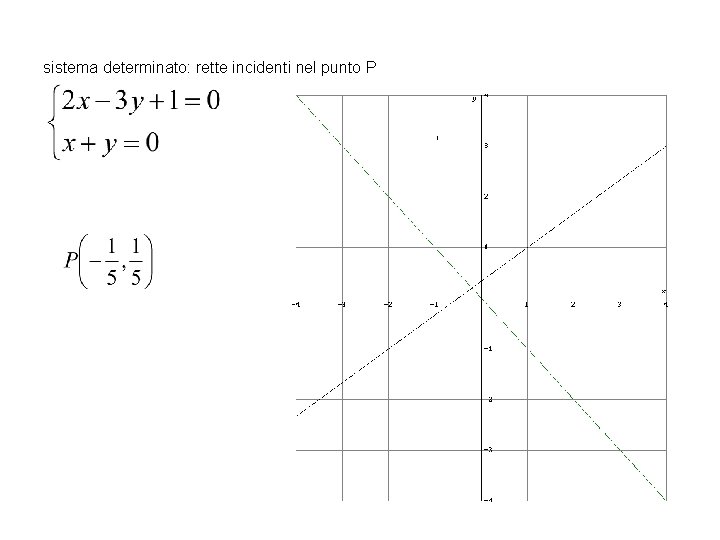
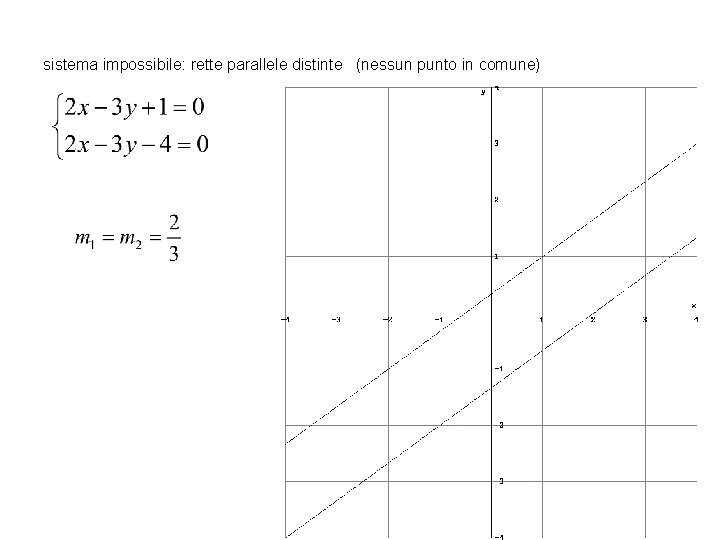
Dato un sistema lineare di due equazioni in due incognite • Se allora le rette corrispondenti alle due equazioni del sistema sono incidenti (o secanti) e il sistema è DETERMINATO • Se allora le rette corrispondenti alle due equazioni del sistema sono parallele distinte e il sistema è IMPOSSIBILE • Se allora le rette corrispondenti alle due equazioni del sistema sono parallele COINCIDENTI (SOVRAPPOSTE) e il sistema è INDETERMINATO

sistema determinato: rette incidenti nel punto P

sistema impossibile: rette parallele distinte (nessun punto in comune)

sistema indeterminato: rette parallele sovrapposte (tutti i punti in comune)

PUNTO MEDIO DI UN SEGMENTO • Dato un segmento AB le coordinate del punto medio M si trovano così: • Se è noto l’estremo A e il punto medio M, è possibile determinare le coordinate dell’estremo incognito B con la formula: (naturalmente è analogo se l’estremo noto è B e quello incognito è A!)

ASSE DI UN SEGMENTO • Per determinare l’asse di un segmento di cui siano noti gli estremi, è possibile procedere con la definizione. (vedi oltre: metodo 1) • ASSE DI UN SEGMENTO è LA RETTA PERPENDICOLARE AL PUNTO MEDIO DEL SEGMENTO • Oppure considerare l’asse come un luogo di punti. (vedi oltre: metodo 2) • ASSE DI UN SEGMENTO è IL LUOGO DI TUTTI E SOLI I PUNTI EQUIDISTANTI DAGLI ESTREMI DEL SEGMENTO

Metodo 1: Usando la definizione • Si trova il punto medio M del segmento (vedi diapo n. 18) • Si trova la pendenza del segmento (attenzione: non interessa l’equazione completa del segmento, ma basta la sua inclinazione!) • Si scrive l’equazione della retta perpendicolare (vedi diapo n. 8) al segmento AB e passante per il suo punto medio M (retta per un punto assegnato e di coefficiente angolare noto, vedi diapo n. 7)

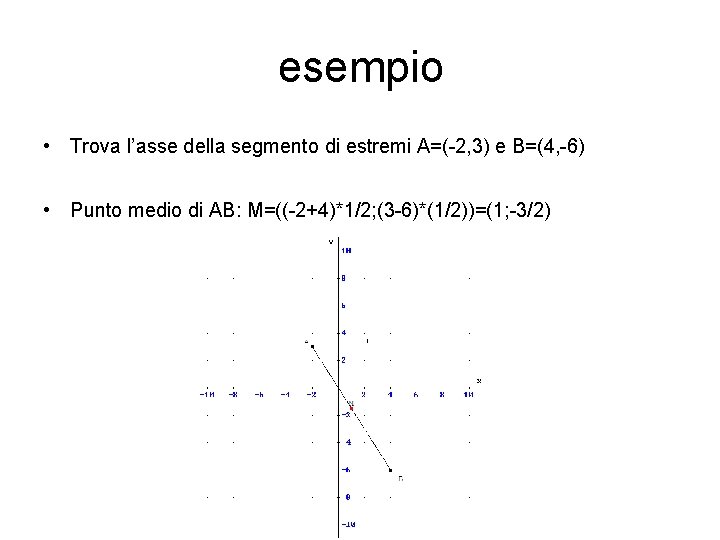
esempio • Trova l’asse della segmento di estremi A=(-2, 3) e B=(4, -6) • Punto medio di AB: M=((-2+4)*1/2; (3 -6)*(1/2))=(1; -3/2)

• Pendenza di AB: vedi diapo n. 4 • m=(-6 -3)/(4+2)=-9/6=-3/2 (infatti è decrescente; si può controllare contando i quadretti!!) • Pendenza m della retta perpendicolare (m antireciproco, vedi diapo n. 8) m asse=2/3 • Formula della retta per un punto e di m dato: y-(-3/2))=2/3(x-1) e cioè: y=2/3 x-13/6 che è l’equazione dell’asse di AB

Disegno

Metodo 2: Usando la definizione • Si utilizza il fatto che, se P(x, y) è un generico punto dell’asse di AB, allora la distanza PA è uguale alla distanza PB. • È questo è vero anche per i loro quadrati:

• Si scrive la distanza punto-punto fra P(x, y) e A, al quadrato • Si scrive la distanza punto-punto fra P(x, y) e B, al quadrato • Si eseguono i calcoli che permettono di eliminare “i quadrati” delle variabili • Si ottiene l’equazione di una retta che rappresenta l’asse del segmento AB

esempio • Trova l’asse della segmento di estremi A=(-2, 3) e B=(4, -6) • Distanza al quadrato fra P e A: • Distanza al quadrato fra P e B: • Eguagliando le distanze e sviluppando i quadrati: • semplificando si trova: y=2/3 x-13/6 che è l’equazione dell’asse di AB

BISETTRICE DI UN ANGOLO • • • Sapendo che la bisettrice di un angolo è il luogo di tutti e soli i punti equidistanti dai lati dell’angolo (dimostrare per esercizio!!) se sono note le equazioni delle rette lati di tale angolo, è possibile, mediante la formula della distanza punto- retta, scrivere l’equazione per trovare la bisettrice; Il punto è il generico punto P(x, y) della bisettrice e le rette da cui si calcola la distanza sono, appunto, i lati. È utile ricordare che Il modo in cui “si tolgono” i simboli di valore assoluto, è strettamente legato a quale delle due bisettrici si deve trovare: infatti, poiché due rette incidenti formano 4 angoli (opposti al vertice ed uguali a coppie fra loro), le bisettrici sono due!