La retta sul piano cartesiano Ogni retta sul

La retta sul piano cartesiano Ogni retta sul piano cartesiano è caratterizzata da una specifica equazione a seconda della posizione che ha rispetto agli assi. Le equazioni di tutte le rette sono di 1° grado, a una o due variabili (x e y). Rette parallele agli assi cartesiani y = q (q x = p (p 0) 0) Rette passanti per l’origine degli assi y = mx Rette generiche y = mx + q

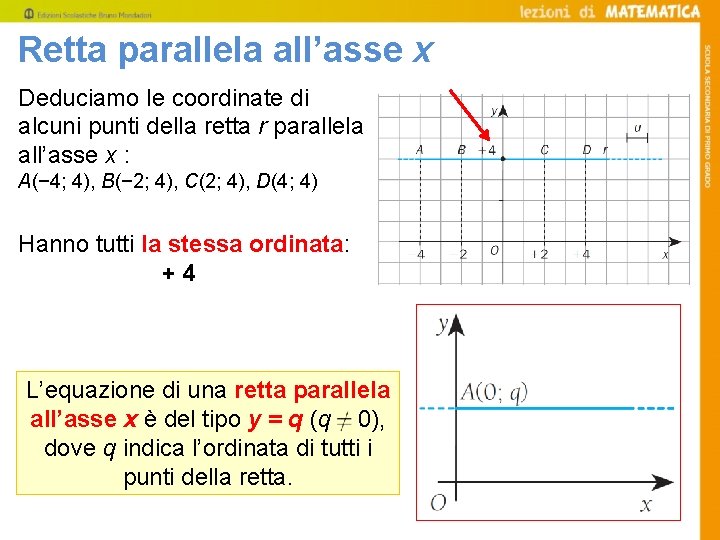
Retta parallela all’asse x Deduciamo le coordinate di alcuni punti della retta r parallela all’asse x : A(− 4; 4), B(− 2; 4), C(2; 4), D(4; 4) Hanno tutti la stessa ordinata: +4 L’equazione di una retta parallela all’asse x è del tipo y = q (q 0), dove q indica l’ordinata di tutti i punti della retta.

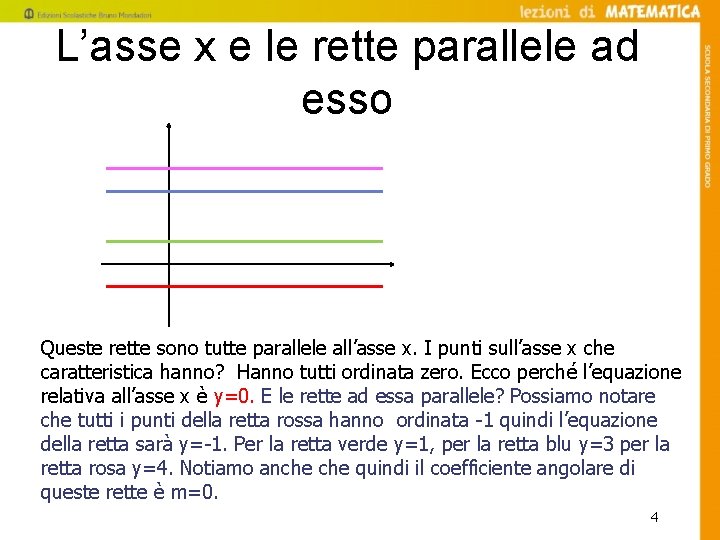
L’asse x e le rette parallele ad esso Queste rette sono tutte parallele all’asse x. I punti sull’asse x che caratteristica hanno? Hanno tutti ordinata zero. Ecco perché l’equazione relativa all’asse x è y=0. E le rette ad essa parallele? Possiamo notare che tutti i punti della retta rossa hanno ordinata -1 quindi l’equazione della retta sarà y=-1. Per la retta verde y=1, per la retta blu y=3 per la retta rosa y=4. Notiamo anche quindi il coefficiente angolare di queste rette è m=0. 4

L’asse y e le rette parallele ad esso Queste rette sono tutte parallele all’asse y. I punti sull’asse y che caratteristica hanno? Hanno tutti l’ascissa zero. Ecco perché l’equazione relativa all’asse y è x=0. e le rette ad essa parallele? Possiamo notare che tutti i punti della retta rossa hanno ascissa -2 quindi l’equazione della retta sarà x=-2. per la retta verde x=2, per la retta blu x=4 per la retta rosa x=6. Notiamo anche il coefficiente angolare di queste 5 rette è m=∞.

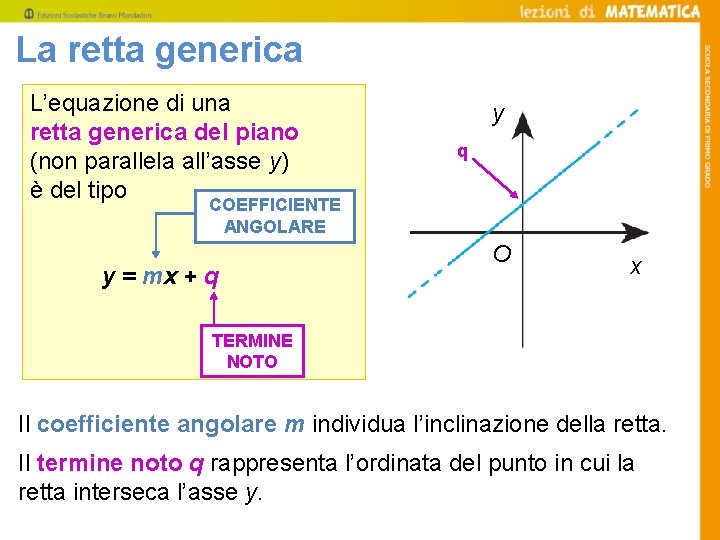
La retta generica L’equazione di una retta generica del piano (non parallela all’asse y) è del tipo y q COEFFICIENTE ANGOLARE y = mx + q O x TERMINE NOTO Il coefficiente angolare m individua l’inclinazione della retta. Il termine noto q rappresenta l’ordinata del punto in cui la retta interseca l’asse y.

Il coefficiente angolare m Il coefficiente angolare è strettamente legato alla misura dell’angolo che la retta forma con il semiasse orientato positivamente delle ascisse 7

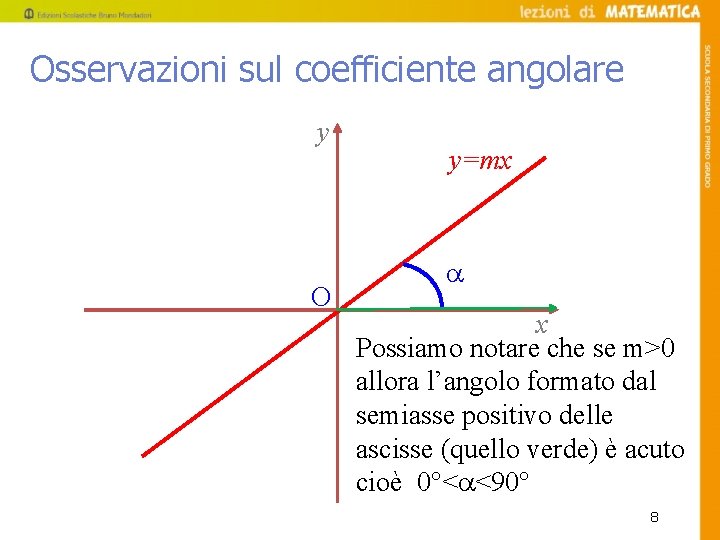
Osservazioni sul coefficiente angolare y O y=mx x Possiamo notare che se m>0 allora l’angolo formato dal semiasse positivo delle ascisse (quello verde) è acuto cioè 0°< <90° 8

Quando l’angolo è ottuso… y y=mx O Possiamo notare che se m<0 allora l’angolo formato dal semiasse positivo delle ascisse (quello verde) è ottuso cioè 90°< <180° x 9

Alcuni esempi • La retta s è parallela all’asse x. Per scrivere la sua equazione consideriamo l’ordinata di uno solo dei suoi punti: B(0; − 1). L’equazione della retta s è: y = − 1 Il valore assoluto dell’ordinata è la misura della distanza della retta dall’asse x: Prova tu • Traccia sulla retta y = − 1 dell’esempio un qualsiasi punto diverso da B: quali sono le sue coordinate? C (. . . . ) 1 Quanto misura la sua distanza dalla retta? d. . .

Retta parallela all’asse y Deduciamo le coordinate di alcuni punti della retta t parallela all’asse y : A(3; 2), B(3; 1), C(3; − 1), D(3; − 2) Hanno tutti la stessa ascissa: +3

Alcuni esempi • La retta s è parallela all’asse y. Per scrivere la sua equazione utilizziamo l’ascissa di uno solo dei suoi punti: A(- ; 0) 23 L’equazione della retta s è: x = - 23 Il valore assoluto dell’ascissa è la misura della distanza della retta dall’asse y: Prova tu • Rappresenta nel piano cartesiano il punto P (4; 2), la retta r passante per P e parallela all’asse x e la retta s, passante per P e parallela all’asse y. Scrivi l’equazione di ognuna delle due rette.

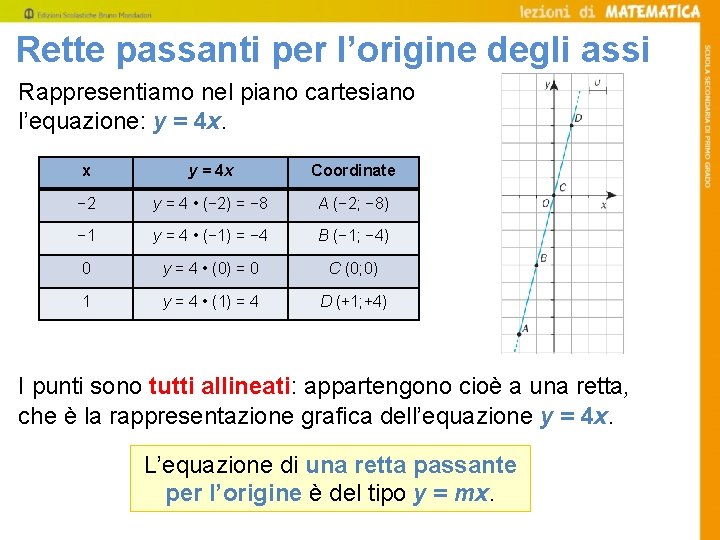
Rette passanti per l’origine degli assi Rappresentiamo nel piano cartesiano l’equazione: y = 4 x. x y = 4 x Coordinate − 2 y = 4 • (− 2) = − 8 A (− 2; − 8) − 1 y = 4 • (− 1) = − 4 B (− 1; − 4) 0 y = 4 • (0) = 0 C (0; 0) 1 y = 4 • (1) = 4 D (+1; +4) I punti sono tutti allineati: appartengono cioè a una retta, che è la rappresentazione grafica dell’equazione y = 4 x. L’equazione di una retta passante per l’origine è del tipo y = mx.

Disegniamo una retta Rappresentiamo nel piano cartesiano l’equazione: y = 2 x − 1 x y = 2 x − 1 Coordinate − 2 y = 2 • (− 2) − 1 = − 5 A (− 2; − 5) − 1 y = 2 • (− 1) − 1= − 3 B (− 1; − 3) 0 y = 2 • (0) − 1 = -1 C (0; − 1) + 1 2 1 y = 2 • (+ 1 )− 1=0 2 y = 2 • (1) − 1 = 1 D (+ 1 ; 0) 2 E (+1; +1) Rappresentando i punti A, B, C, D, E nel piano cartesiano e unendoli, otteniamo una retta non passante per l’origine O.

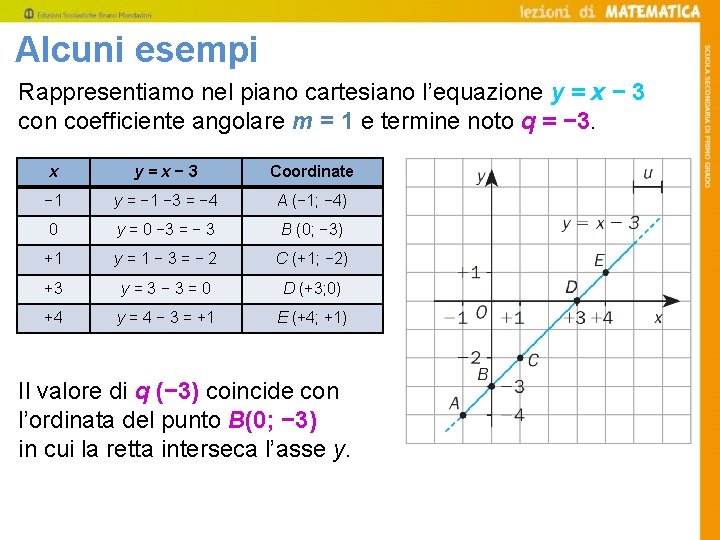
Alcuni esempi Rappresentiamo nel piano cartesiano l’equazione y = x − 3 con coefficiente angolare m = 1 e termine noto q = − 3. x y=x− 3 Coordinate − 1 y = − 1 − 3 = − 4 A (− 1; − 4) 0 y = 0 − 3 = − 3 B (0; − 3) +1 y=1− 3=− 2 C (+1; − 2) +3 y=3− 3=0 D (+3; 0) +4 y = 4 − 3 = +1 E (+4; +1) Il valore di q (− 3) coincide con l’ordinata del punto B(0; − 3) in cui la retta interseca l’asse y.

Prova tu • Rappresenta nel piano cartesiano la retta di equazione y = x + 2. In quale punto interseca l’asse y ? ……. . . B(0; 2) x y = x +2 Coordinate

Su e giù per la scala mobile… Una scala mobile parte e si muove con una velocità costante di 2 m/s. La legge del suo moto rettilineo uniforme è: s=v • t =2 • t È una funzione di proporzionalità diretta e il suo dominio è R+. Il grafico è una semiretta. Dopo 3 secondi dalla partenza, quanti metri ha percorso la scala mobile? ……………. . 6 m

Esercitati • Completa con i termini e i simboli ascissa, ordinata, x, y. L’equazione di una retta: parallela all’asse. . . . è del tipo y = q, dove q indica x ordinata l’. . . . di tutti i punti della retta; parallela all’asse. . . . è del tipo x = p, dove p indica y ascissa l’. . . . di tutti i punti della retta. • Riconosci tra le seguenti equazioni quelle che rappresentano rette parallele all’asse x e rette parallele all’asse y. a) y = 7 x b) y = 7 c) x = 7 d) y = x + 7 e) x = 5 f) y = 1 7 parallela asse x: b, f parallela asse y: c, e

Esercitati • Stabilisci se le seguenti affermazioni sono vere o false e correggi quelle false. Data l’equazione di una retta passante per l’origine… x il suo coefficiente angolare è m = y (x, y V F 0) x se m > 0 allora giace nel III quadrante x se m < 0 allora giace nel II e nel IV quadrante x • Scrivi l’equazione e disegna una retta passante per l’origine e che giace: nel I e nel III quadrante: . . nel II e nel IV quadrante: . . Correzione m= y x

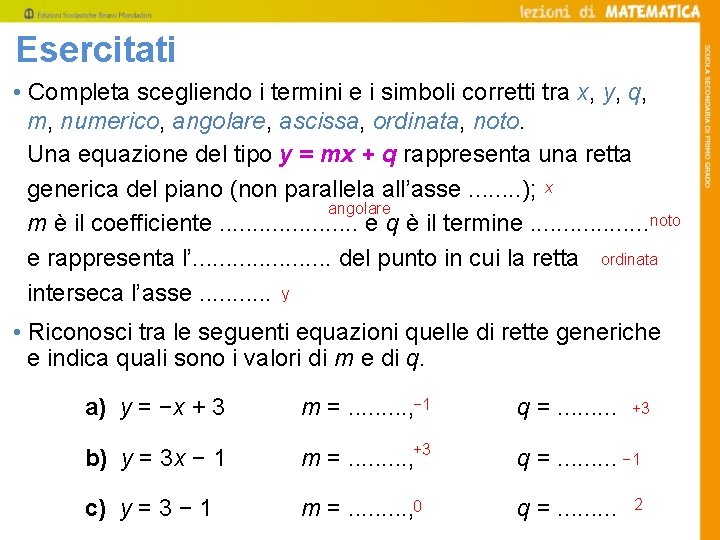
Esercitati • Completa scegliendo i termini e i simboli corretti tra x, y, q, m, numerico, angolare, ascissa, ordinata, noto. Una equazione del tipo y = mx + q rappresenta una retta generica del piano (non parallela all’asse. . . . ); x angolare m è il coefficiente. . . . . e q è il termine. . . . noto e rappresenta l’. . . . . del punto in cui la retta ordinata interseca l’asse. . . y • Riconosci tra le seguenti equazioni quelle di rette generiche e indica quali sono i valori di m e di q. a) y = −x + 3 m =. . , − 1 q =. . b) y = 3 x − 1 m =. . , +3 q =. . − 1 c) y = 3 − 1 m =. . , 0 q =. . +3 2

• • • Esercitazione web n° 2 Esercitazione web n° 3 Esercitazione web n° 5 Esercitazione web n° 7 Esercitazione web n° 9 Ogni giorno vi darò compiti per la lezione seguente…. . Chi si ama mi segua!!