ASCISSA SOPRA UNA RETTA Sia data una retta

ASCISSA SOPRA UNA RETTA Sia data una retta r, si fissi: 1) Un verso positivo di percorrenza 2) Un punto O detto Origine 3) Un segmento u detto unità di misura O r- u r+ r

ASSE DELLE ASCISSE • Preso un punto P sull’asse delle ascisse, a P si può sempre associare x. P R, ovvero la misura del segmento OP, presa col segno + (-) se P appartiene al semiasse positivo (negativo) x. P è chiamata ascissa di P • Viceversa, x R ! P r : x= x. P. • Esiste una corrispondenza biunivoca tra numeri reali e punti della retta.

COORDINATE CARTESIANE NEL PIANO Date 2 rette r 1 e r 2 non parallele ed incidenti nel punto O, si fissi su ciascuna: 1) Un verso positivo di percorrenza 2) Una unità di misura Si ottiene così un sistema di riferimento cartesiano Ortogonale / obliquo Monometrico / dimetrico

COORDINATE CARTESIANE NEL PIANO • Si dimostra che ad ogni punto P del piano si può associare una coppia ordinata P=(x, y) II I IV

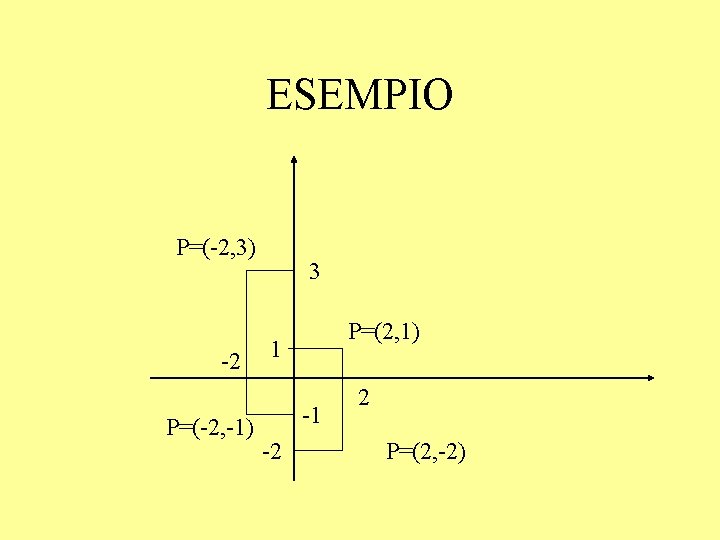
ESEMPIO P=(-2, 3) -2 P=(-2, -1) 3 P=(2, 1) 1 -1 -2 2 P=(2, -2)

ANGOLO • Prendiamo due semirette a e b aventi la stessa origine, il piano resta diviso in due parti, ciascuna delle quali viene detta angolo.

ANGOLO ORIENTATO • Verso positivo di rotazione antiorario b + a a b

ARCO • La parte di circonferenza compresa tra i lati dell’angolo. B A

SISTEMI DI MISURA DI ANGOLI • SESSAGESIMALE: grado sessagesimale = la 360 a parte dell’angolo giro. • CENTESIMALE: grado centesimale = la 400 a parte dell’angolo giro • RADIANTE

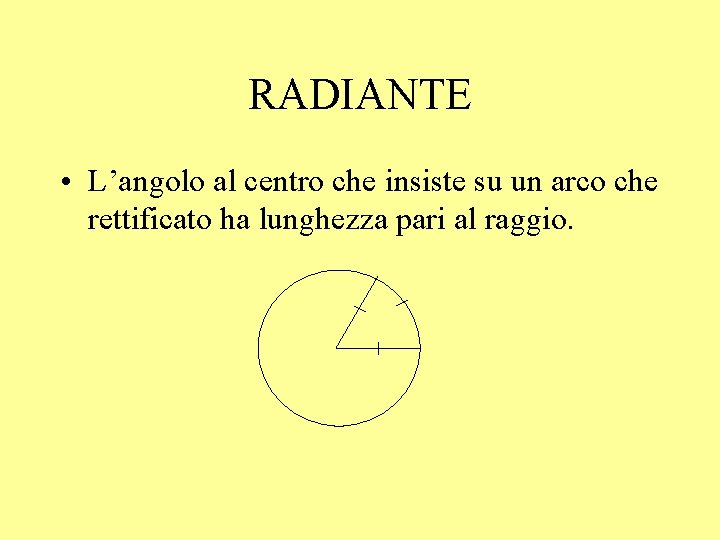
RADIANTE • L’angolo al centro che insiste su un arco che rettificato ha lunghezza pari al raggio.

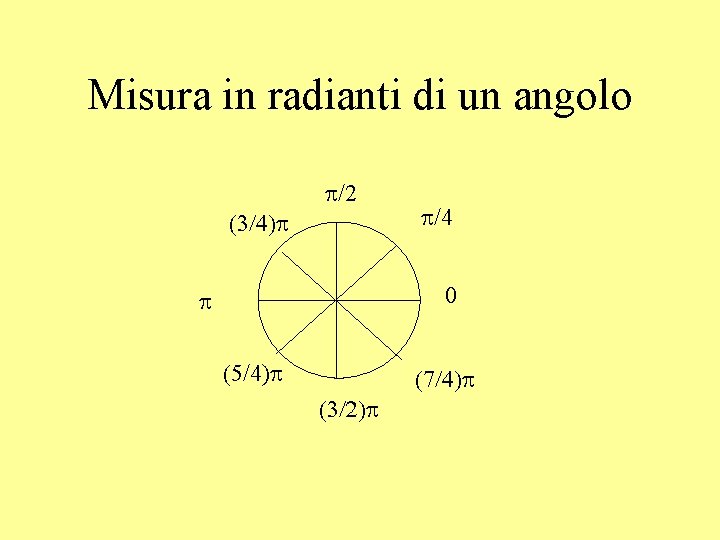
Misura in radianti di un angolo • È uguale alla misura dell’arco diviso il raggio: • Angolo giro = 2 pr / r = 2 p • Angolo piatto = pr / r = p • Angolo retto = p/2

Misura in radianti di un angolo p/2 (3/4)p p/4 0 p (5/4)p (7/4)p (3/2)p

Misura in radianti di un angolo (4/6)p p/2 (5/6)p p/6 0 p (11/6)p (7/6)p (8/6)p (2/6)p (3/2)p (10/6)p

Misura in radianti di un angolo • Per passare dal sistema sessagesimale a quello radiante: 360 : 2 p = as : ar Ex: 360 : 2 p = 20 : ar ar = p/9

CIRCONFERENZA GONIOMETRICA • Fissato nel piano un sistema di riferimento cartesiano, la circonferenza con raggio 1 e centro nell’origine è detta circonferenza y goniometrica. A=(1, 0) x

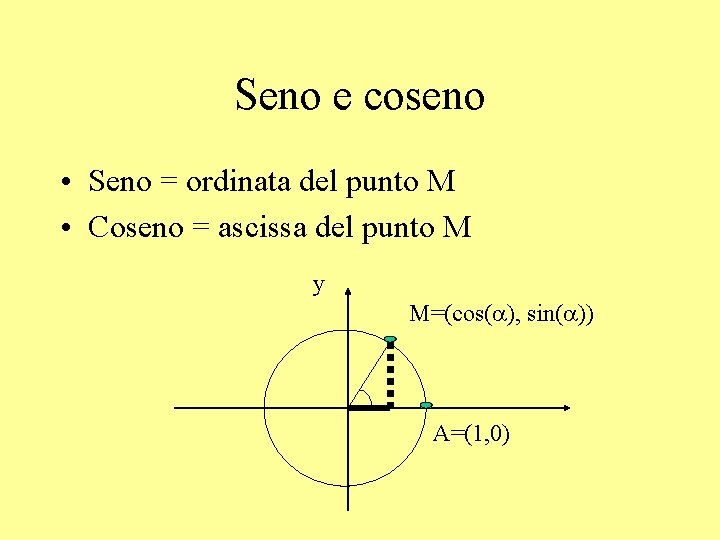
Seno e coseno • Seno = ordinata del punto M • Coseno = ascissa del punto M y M=(cos(a), sin(a)) A=(1, 0)

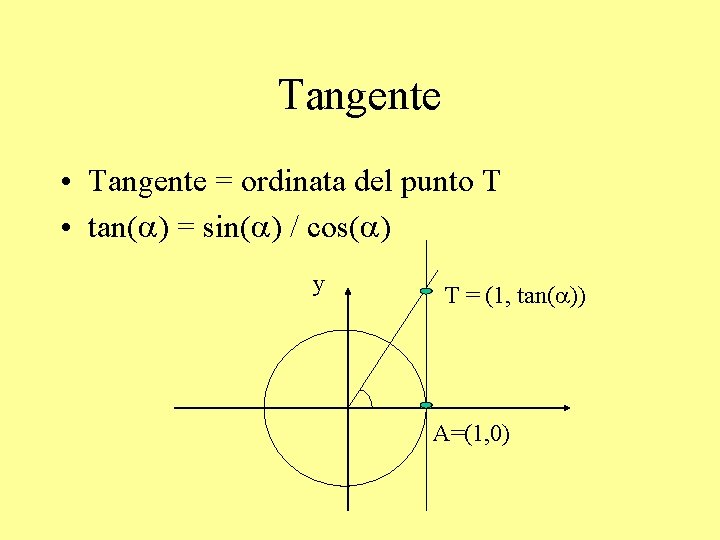
Tangente • Tangente = ordinata del punto T • tan(a) = sin(a) / cos(a) y T = (1, tan(a)) A=(1, 0)

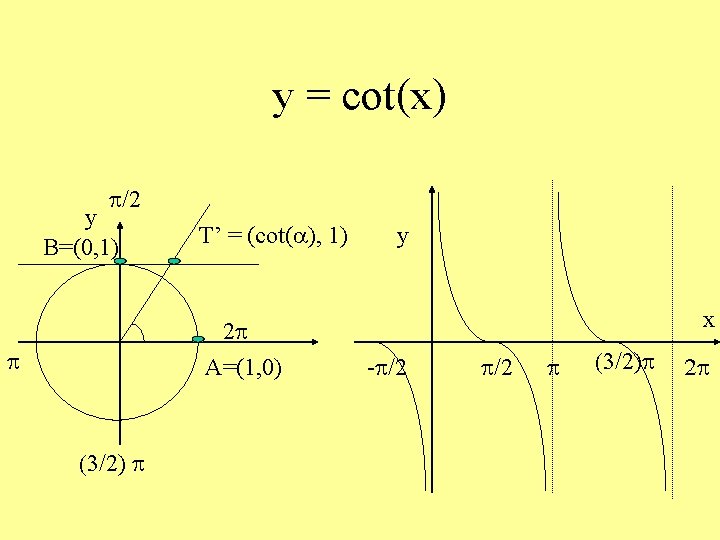
Cotangente = ascissa del punto T’ cot(a) = 1 / tan(a) = cos(a) / sin(a) y B=(0, 1) T’ = (cot(a), 1) A=(1, 0)

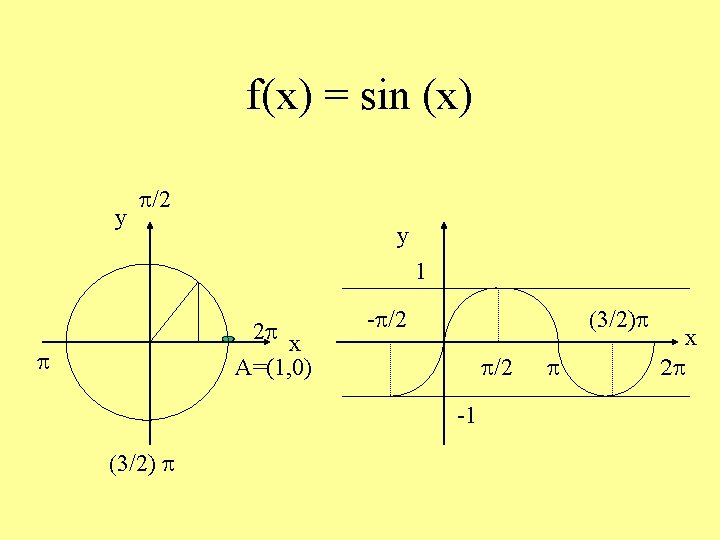
f(x) = sin (x) y p/2 y 1 2 p x A=(1, 0) p (3/2)p -p/2 -1 (3/2) p p x 2 p

Funzione seno • Dominio R • Codominio [-1, 1] • Periodica di periodo 2 p

y = cos (x) y p/2 y 2 p x A=(1, 0) p (3/2) p -p/2 p (3/2)p x

Funzione coseno • Dominio R • Codominio [-1, 1] • Periodica di periodo 2 p

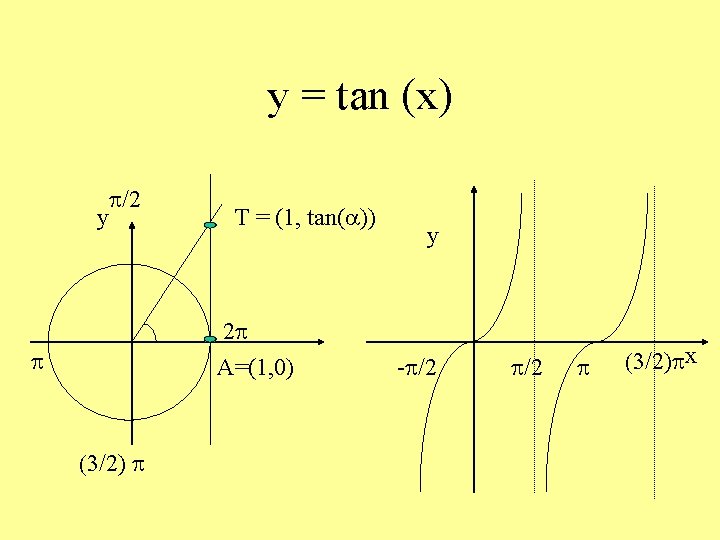
y = tan (x) p/2 y T = (1, tan(a)) 2 p A=(1, 0) p (3/2) p y -p/2 p (3/2)px

Funzione tangente • Dominio = R p/2 + kp k Z • Codominio = R • Periodica di periodo p

y = cot(x) p/2 y B=(0, 1) T’ = (cot(a), 1) 2 p A=(1, 0) p (3/2) p y x -p/2 p (3/2)p 2 p

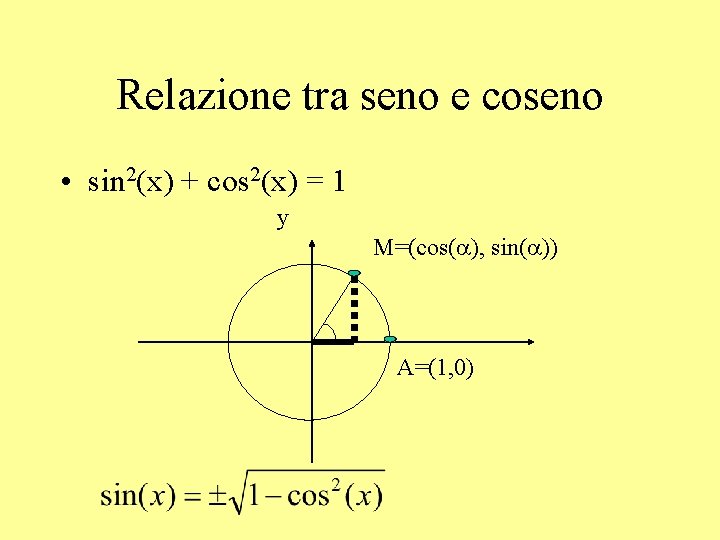
Relazione tra seno e coseno • sin 2(x) + cos 2(x) = 1 y M=(cos(a), sin(a)) A=(1, 0)

Relazione tra seno e coseno • Esempi: cos (x) = ½ x [0, p/2]

Relazione tra seno, coseno e tangente • sin 2(x) + cos 2(x) = 1

Relazione tra seno, coseno e tangente • sin(x) = tan(x) cos(x)

Valori in archi particolari : p/6

Valori in archi particolari: p/3

Valori in archi particolari: p/4

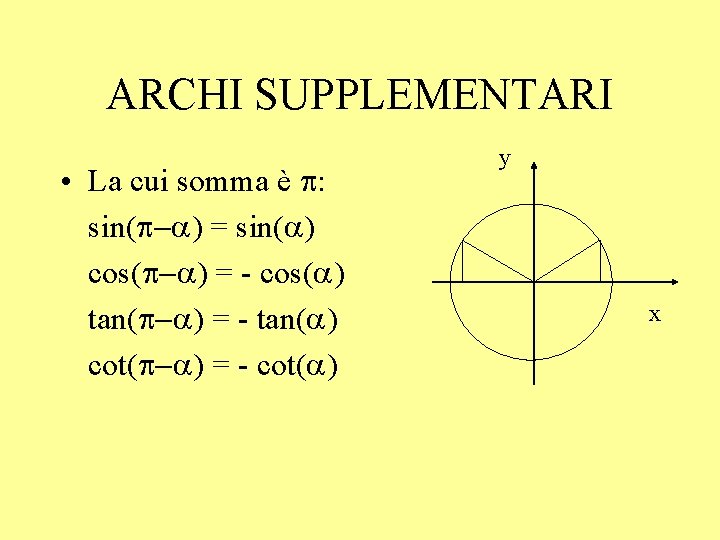
ARCHI SUPPLEMENTARI • La cui somma è p: sin(p-a) = sin(a) cos(p-a) = - cos(a) tan(p-a) = - tan(a) cot(p-a) = - cot(a) y x

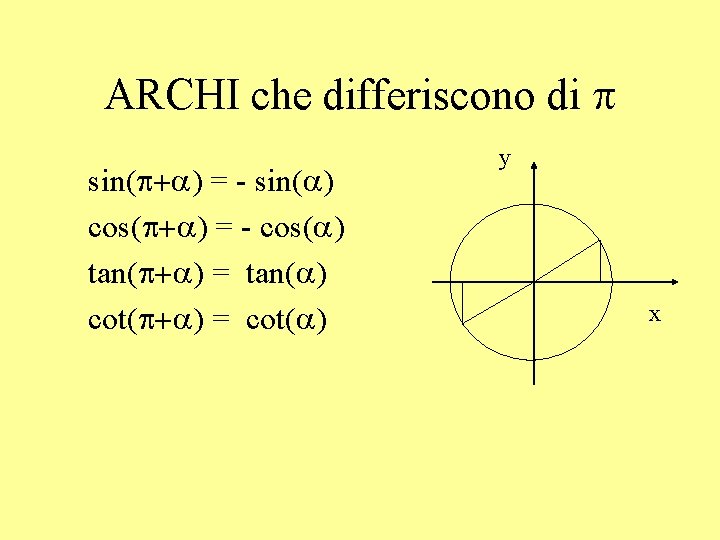
ARCHI che differiscono di p sin(p+a) = - sin(a) cos(p+a) = - cos(a) tan(p+a) = tan(a) cot(p+a) = cot(a) y x

ARCHI la cui somma è 2 p sin(2 p-a) = - sin(a) cos(2 p-a) = cos(a) tan(2 p-a) = - tan(a) cot(2 p-a) = - cot(a) y x

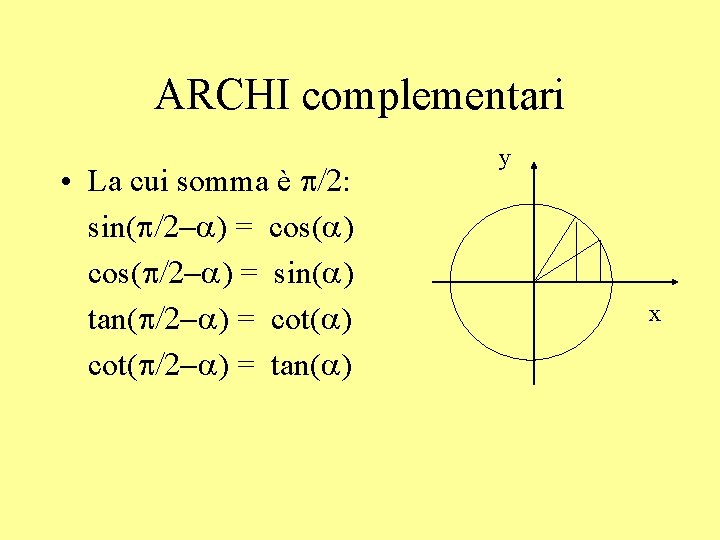
ARCHI complementari • La cui somma è p/2: sin(p/2 -a) = cos(a) cos(p/2 -a) = sin(a) tan(p/2 -a) = cot(a) cot(p/2 -a) = tan(a) y x

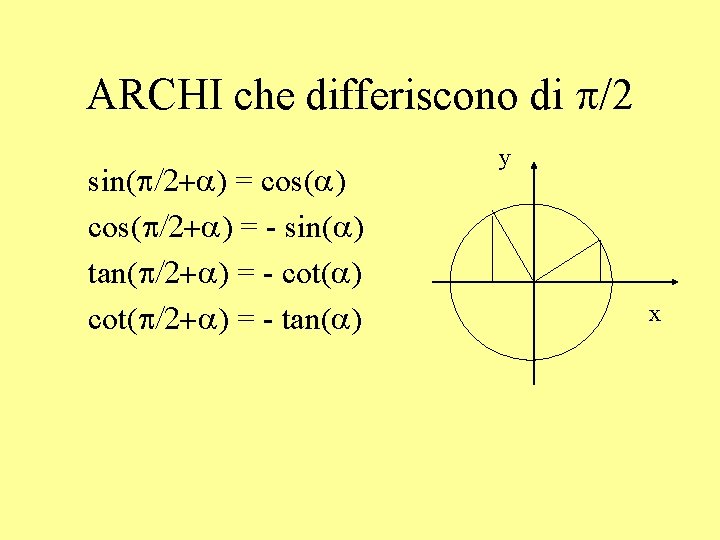
ARCHI che differiscono di p/2 sin(p/2+a) = cos(a) cos(p/2+a) = - sin(a) tan(p/2+a) = - cot(a) cot(p/2+a) = - tan(a) y x

EQUAZIONI GONIOMETRICHE • Equazioni in cui le variabili compaiono come argomento di funzioni goniometriche. sin(x) = a cos(x) = a |a| >1 impossibile a=1 1 soluzione fondamentale a= -1 1 soluzione fondamentale -1< a < 1 2 soluzioni fondamentali

EQUAZIONI GONIOMETRICHE tan(x) = a cot(x) = a Mai impossibile 1 soluzione fondamentale

ESEMPI sin(x) = ½ x 1 = p/6 + 2 kp x 2 = (5/6) p + 2 kp x 1 = p/4 + 2 kp x 2 = (7/4) p + 2 kp

ESEMPI • tan(x) = 1 x = p/4 + kp • cot(x) = -1 x = (3/4)p + kp