Aplicaciones del Modelo de Variograma Aplicaciones v Definir

















![Ø Calculados los valores de las matrices [ C] y [ D], el objetivo Ø Calculados los valores de las matrices [ C] y [ D], el objetivo](https://slidetodoc.com/presentation_image_h/aa74ea05769acebbcad3422941d72bae/image-22.jpg)




- Slides: 27

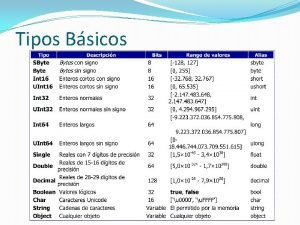
Aplicaciones del Modelo de Variograma

Aplicaciones v Definir la variabilidad de un yacimiento. a) Concepto de soporte b) Varianza de dispersión (c/distintos soportes) c) Varianza de estimación v Estimación de leyes por Kriging

v Soporte: es el término que se usa en la geoestadística para describir el volumen en función del cual se define una ley. v A medida que aumenta el tamaño de la muestra (o del soporte de la muestra), la varianza de las leyes resultantes disminuye. v El cambio en la varianza debido al cambio en el volumen se denomina la relación volumen-varianza. v Existe un tamaño mínimo de bloque se puede seleccionar ya sea como mineral o estéril. El tamaño del bloque se denomina la unidad minera selectiva o UMS. v A medida que <<UMS la varianza aumenta.

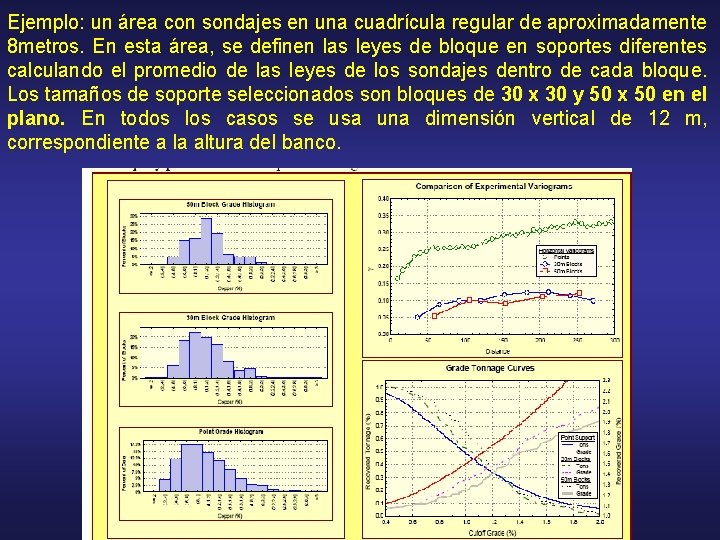
Ejemplo: un área con sondajes en una cuadrícula regular de aproximadamente 8 metros. En esta área, se definen las leyes de bloque en soportes diferentes calculando el promedio de las leyes de los sondajes dentro de cada bloque. Los tamaños de soporte seleccionados son bloques de 30 x 30 y 50 x 50 en el plano. En todos los casos se usa una dimensión vertical de 12 m, correspondiente a la altura del banco.

Conclusión • ¡NO SE PUEDE ASEVERAR LAS RESERVAS EXPLOTABLES DE UN PROYECTO SIN FIJAR UN TAMAÑO DE SOPORTE¡

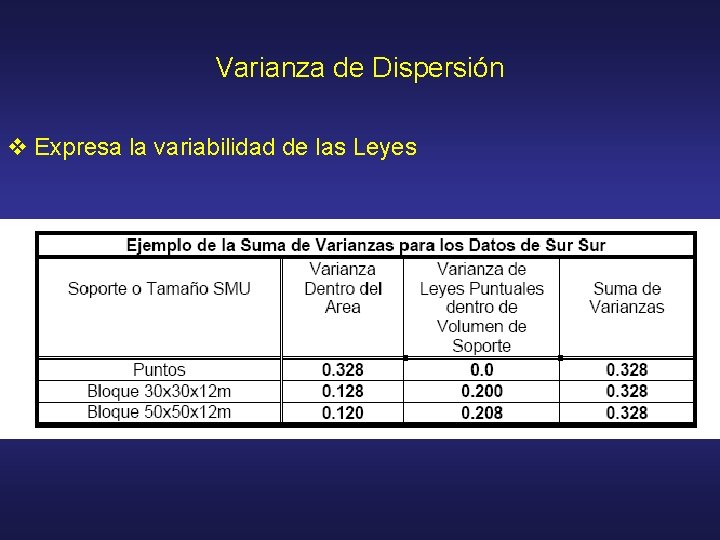
Varianza de Dispersión v Expresa la variabilidad de las Leyes

D 2 (0 / A ) = D 2 (v / A ) + D 2(0 / v ) • • D 2 : Varianza 0 : Muestras puntuales V: Bloques A : Area Varianza de las muestras puntuales en un área = Varianza de los Bloques del área + Varianza de las muestras puntuales en los bloques

Se demostró que la Varianza disminuye al aumentar el tamaño del soporte v El modelo de variograma se puede usar para predecir la varianza de leyes en un soporte de cualquier tamaño dentro de cualquier volumen. v. v vi es reemplazado por las leyes de los datos individuales y el término m es reemplazado por la ley media del bloque y la varianza de dispersión se interpreta como la varianza de las leyes de muestra dentro del bloque.

v En la primera expresión, la diferencia al cuadrado media se computa en todos los pares de puntos que definen el volumen v. v Los términos en esta expresión se pueden expandir (véase J. Sullivan, 1998) para mostrar: .

Se puede ver de la similitud de ambas expresiones que la varianza de dispersión de las leyes de muestra dentro de un volumen es igual al medio de la función de variograma en función del volumen. Se puede escribir matemáticamente: • Basado en esta relación se puede expresar cualquier varianza de dispersión en términos de la función de variograma

Varianza de Estimación v Mientras que la varianza de dispersión expresa la variabilidad de las leyes, la varianza de estimación expresa la variabilidad asociada con una estimación o, en otras palabras, expresa la varianza de los errores de estimación. v La varianza de estimación es una medida de la dispersión de los errores aleatorios, ya que se requiere que el estimador no tenga ningún sesgo y, por lo tanto, el error sistemático será cero. v Se puede definir la varianza de estimación para cualquier tipo lineal de estimador, no solamente para el estimador de kriging. v La característica relevante del estimador de kriging es que el kriging proporciona el estimador (ponderador) que minimiza la varianza de estimación. Así que, la varianza de estimación será más pequeña cuando se aplica el kriging.

Tipos de errores Sistemáticos y Aleatorios La precisión describe el error aleatorio o las fluctuaciones en torno al valor verdadero mientras que la exactitud describe el error sistemático o el sesgo.

v El error de estimación para un punto (E), será la diferencia entre Z*, (la verdadera ley del punto), y la Ley (Zx) que es resultado de su cálculo a través de leyes xi afectados por un coeficiente Ki. • Ε = Z* - Zx = Z* - (xi. Ki ) v Si el estimador no tiene sesgo (error sistemático nulo), la distribución de los errores debería seguir una distribución normal. v El estimador usado tiene la forma : donde los representan las ponderaciones asignadas a cada dato. La única restricción para las ponderaciones es que sumen uno,

v La varianza de estimación va a depender de las distancias estadísticas (Y), promedio entre los datos y el bloque. Puesto que el modelo de variograma es una función creciente, el error de estimación aumenta o diminuye con las distancias desde las muestras al centro del bloque. (es lo que expresa el 1 er término de la fórmula). v El segundo término de la expresión involucra el promedio de la función del variograma entre las ubicaciones de las muestras. Este término es negativo, así que la varianza de estimación disminuye a medida que este término aumenta (datos distanciados). Si los datos se encuentran agrupados, las muestras básicamente investigarán el mismo punto en el espacio y, como consecuencia, mucha de la información se hará redundante (aumenta la varianza de estimación). v El tercer término examina el promedio de la función del variograma dentro del bloque mismo. A medida que aumenta el tamaño del bloque, también aumenta ese término, reduce la varianza de estimación.

MÉTODO GEOESTADÍSTICO KRIGEADO

• La geoestadística ofrece un método de estimación de reservas, usando el variograma, llamado krigeado. Se utiliza en la evaluación de yacimientos para estimar el valor de una variable regionalizada, en un punto o en un bloque, a partir del uso de factores de ponderación. • El método se caracteriza por ser el mejor estimador lineal, insesgado de la variable. • Mejor: por que los factores de ponderación se determinan de tal forma, que la varianza de estimación es mínima. • Lineal: por que es una combinación lineal de la información. • Insesgado: por que en promedio el error es nulo.

Krigeado Puntual • Método de Cálculo: primero hay que determinar los factores de ponderación, para obtener el valor de la variable. • Estos factores se calculan a partir de un sistema de ecuaciones, en que las incógnitas para resolver se obtienen a partir del variograma. • Variable buscada←Z *=∑ W x Z → variables dadas ↓ • Ponderador a determinar • ↓ • [ C ]. [ W ] =[ D ] • C = varianza de los puntos conocidos (en función de la distancia). • D = varianza de los puntos conocidos y el punto a estimar.

• Resumiendo las ecuaciones están formadas por tres tipos de componentes: • A) Los factores de ponderación (W). • B) Los factores que multiplican a W ; Yh de variables conocidas. • C) Los valores de Y 0 del punto cuestión y los conocidos. • La diferencia con inverso a la distancia es que en el Krig. Se utilizan las distancias estadísticas, no la geométricas. Ø Con efecto pepita puro : no se puede usar Krig. Ø Con efecto pepita >>: aumenta la varianza del Krig. Ø Con alcance >>: disminuye la varianza del Krig.

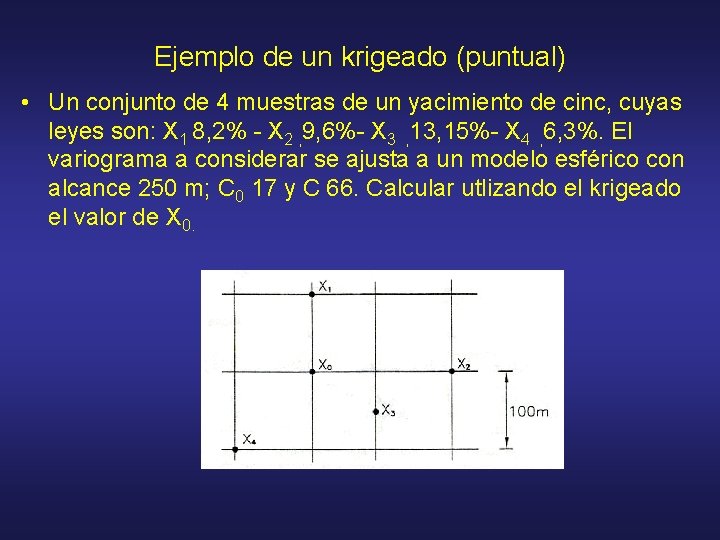
Ejemplo de un krigeado (puntual) • Un conjunto de 4 muestras de un yacimiento de cinc, cuyas leyes son: X 1 8, 2% - X 2 , 9, 6%- X 3 , 13, 15%- X 4 , 6, 3%. El variograma a considerar se ajusta a un modelo esférico con alcance 250 m; C 0 17 y C 66. Calcular utlizando el krigeado el valor de X 0.

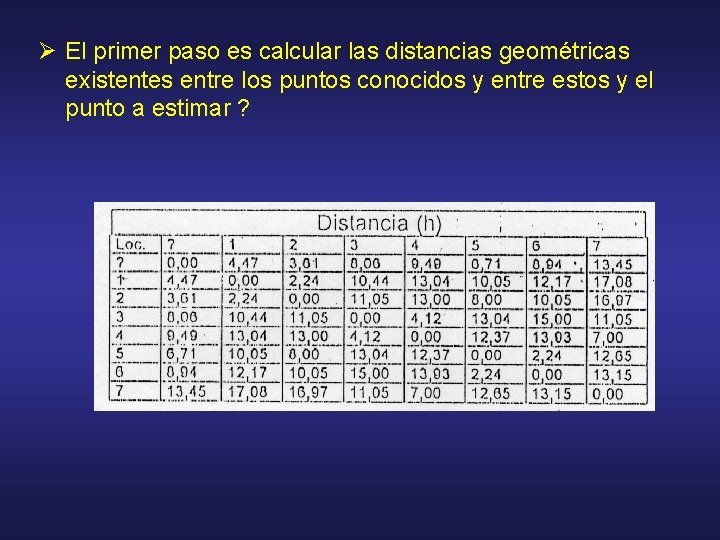
Ø El primer paso es calcular las distancias geométricas existentes entre los puntos conocidos y entre estos y el punto a estimar ?

Ø Luego con el modelo de Varianza o Covariaza (λ-C) y la tabla de distancias, se calculan las matrices [ C] y [ D]. Se transforman las distancias geométricas en estadísticas.
![Ø Calculados los valores de las matrices C y D el objetivo Ø Calculados los valores de las matrices [ C] y [ D], el objetivo](https://slidetodoc.com/presentation_image_h/aa74ea05769acebbcad3422941d72bae/image-22.jpg)
Ø Calculados los valores de las matrices [ C] y [ D], el objetivo es obtener los valores de los ponderadores W, que es la incógnita, para eso debe calcularse la matriz inversa de C ► C -1

Ø El siguiente paso para obtener los ponderadores W, es multiplicar cada lado de la ecuación por C -1. ØW = C -1 x D

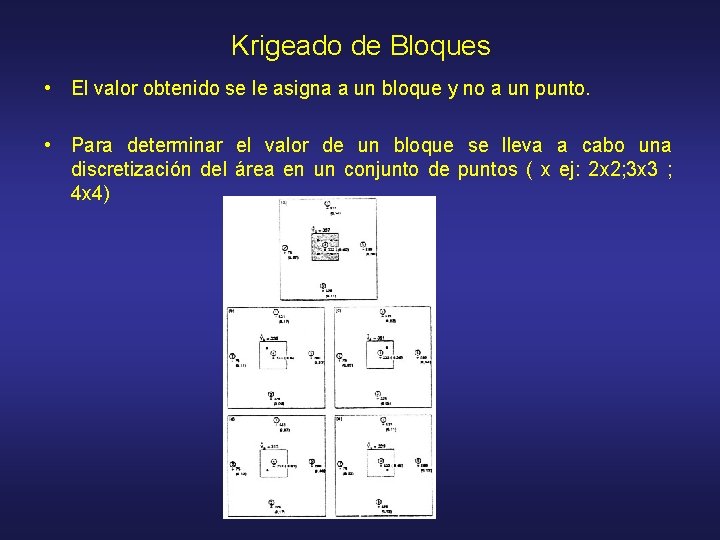
Krigeado de Bloques • El valor obtenido se le asigna a un bloque y no a un punto. • Para determinar el valor de un bloque se lleva a cabo una discretización del área en un conjunto de puntos ( x ej: 2 x 2; 3 x 3 ; 4 x 4)

• Los valores que se obtienen con el krigeado, llevan los correspondientes valores de la varianza de estimación, lo que permite hacer un estudio de la bondad de estimación. • Estos valores pueden ser interpolados y confeccionar un mapa de isovarianzas. • Annels (1991), propone establecer diferentes tipos de reservas en base a los valores de varianza del krigeado. • • Varianza 0 -0, 0075 -0, 0135 >0, 0135 - Categoría Reservas probables Reservas posibles Reservas inferidas

• El resultado se puede proporcionar por bloques o bien por isolíneas a partir de los bloques. • Para el cálculo de reserva de cada bloque, se deberá multiplicar su superficie x potencia x densidad. • Las reservas totales se pueden determinar: • Estimando el tonelaje y el error de estimación. • Estimando la ley media y el error de estimación.

Bibliografía • Bustillo Revuelta, M. y López Jimeno, C. , 1997: Manual de evaluación y diseño de explotaciones mineras. Madrid. ISBN 84 -921708 -2 -4. • ANNELS, A. E. (1991). Mineral deposit evaluation. A practical approach. Ed. Chapman & Hall, London. • TULCANAZA, E. (1992). Técnicas geoestadísticas y criterios técnicoeconómicos para la estimación y evaluación de yacimientos mineros. . E. Tulcanaza, Santiago, Chile. • Jeff Sullivan 1998. Curso Geoestadística para Minería. Codelco Santiago d e Chile.
 Anisotropia zonal
Anisotropia zonal Trabajo virtual estructuras
Trabajo virtual estructuras Definir variables en c
Definir variables en c Objetivo de relaciones interpersonales
Objetivo de relaciones interpersonales Pontos complanares
Pontos complanares Definir el alcance de un proyecto
Definir el alcance de un proyecto Como definir un plano
Como definir un plano Definir weblog
Definir weblog 8 remedios naturales temperancia
8 remedios naturales temperancia Horizontal
Horizontal El arco reflejo
El arco reflejo Comment definir le mode epg et regler le timeshift?
Comment definir le mode epg et regler le timeshift? Definir huidizo
Definir huidizo Definir oxydant
Definir oxydant Definir
Definir Definir
Definir Definir esquivo
Definir esquivo Boom hispanoamericano
Boom hispanoamericano Définir les objectifs de communication
Définir les objectifs de communication Definir
Definir Vendedor dominante hostil
Vendedor dominante hostil Définir pluriculturel
Définir pluriculturel Como se mide
Como se mide Problemas de sueño y dolor al padecer cáncer
Problemas de sueño y dolor al padecer cáncer Aplicaciones del cloro
Aplicaciones del cloro Aplicaciones del principio de pascal
Aplicaciones del principio de pascal Interpretacion geometrica de valor absoluto
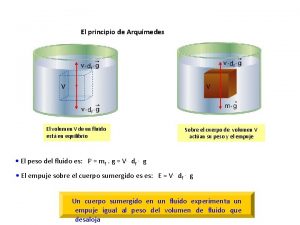
Interpretacion geometrica de valor absoluto Aplicaciones de principio de arquimedes
Aplicaciones de principio de arquimedes