Algorithms for Lattice QCD with Dynamical Fermions A

Algorithms for Lattice QCD with Dynamical Fermions A D Kennedy University of Edinburgh Lattice 2004, Fermilab

Testimonial …The lattice conferences have had a steady diet of spectroscopy and matrix element calculations from these projects. But this year there seemed to be a pause. I think many people have decided that they just cannot push the quark masses down far enough to be interesting, and have gone back to studying (I expect to get a lot of unhappy algorithms. mail about this sentence. ) Tom De. Grand hep-ph/0312241 Algorithms for Lattice QCD 2

Numerical Simulations under Battlefield Conditions: I Algorithms for Lattice QCD 3

Numerical Simulations under Battlefield Conditions: II 4 No continuum limit 4 Two lattice spacings or fewer 4 Autocorrelations ignored 4 Depend on the physics anyhow 4 Naïve volume scaling 4 V for R algorithm 4 V 5/4 for HMC 4 Dynamical quarks 4 No valence mass 4 Two or three flavours 4 CAVEAT EMPTOR! 4 4 4 S Gottlieb (MILC) hep-lat/0402030 K Jansen (tml. QCD and χLF) R Mawhinney (Columbia and RBRC) CP-PACS hep-lat/0404014 CP-PACS and JLQCD Nucl. Phys. B 106 (2002) 195 -196 Algorithms for Lattice QCD 4

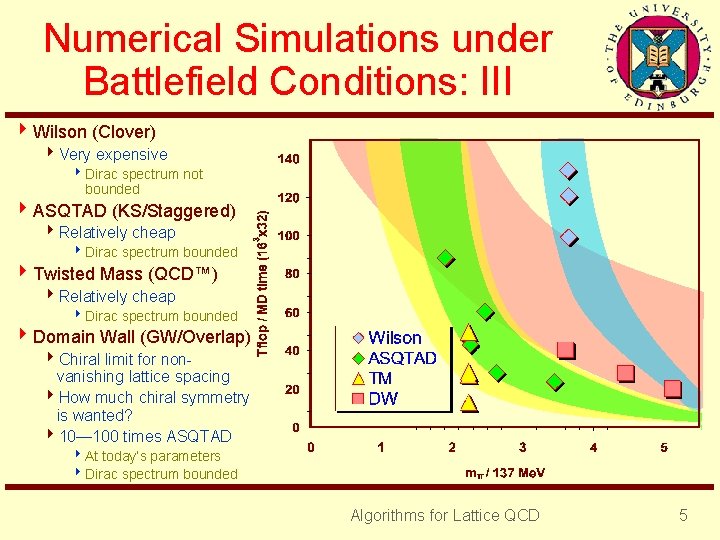
Numerical Simulations under Battlefield Conditions: III 4 Wilson (Clover) 4 Very expensive 8 Dirac spectrum not bounded 4 ASQTAD (KS/Staggered) 4 Relatively cheap 8 Dirac spectrum bounded 4 Twisted Mass (QCD™) 4 Relatively cheap 8 Dirac spectrum bounded 4 Domain Wall (GW/Overlap) 4 Chiral limit for nonvanishing lattice spacing 4 How much chiral symmetry is wanted? 410— 100 times ASQTAD 8 At today’s parameters 8 Dirac spectrum bounded Algorithms for Lattice QCD 5

Why Locality? 4 If a QFT is local then… 4 Cluster decomposition 4(Perturbative) Renormalisability 8 Power counting 8 Universality 8 Improvement 4…otherwise 4 Who knows? Algorithms for Lattice QCD 6

Locality 4 A “wavefunction” is obtained by applying a lattice Dirac operator to a point source 4 A QFT is ultralocal if the wavefunction has “compact support, ” 4 A QFT is local if the wavefunction has “fast decrease, ” Algorithms for Lattice QCD 7

Is 1/2 M Finite Volume Local? Improvement Lattice Spacing 4 [1] B Bunk, M Della Morte, K Jansen & F Knechtli hep-lat/0403022 4 [2, 3] A Hart and E Müller hep-lat/0406030 4 S Dürr & C Hoebling hep-lat/0311002 Algorithms for Lattice QCD 8

Hidden Locality 4 It is easy to transform a manifestly local theory into an equivalent but non-manifestly local form… 4 We use this freedom to replace fermion fields with a non-manifestly local fermion determinant 4 To introduce a pseudofermion representation 4 To simulate the square root of a determinant 4…but in general a non-local theory has no reason to be equivalent to a local one Algorithms for Lattice QCD 9

Fewer Staggered “Tastes” 4 Staggered quarks come in four degenerate tastes 4 det(M) in functional integral 4 det(M)1/2 for two tastes 8 Generate gauge configurations with square root weight using R, PHMC, or RHMC algorithms 4 Is this a local field theory? 8 local M’ such that det(M’) = det(M 1/2)? 8 Must use M’ for valence quarks too for a consistent unitary theory 4 Mixed action computations? 4 4 taste valence + 2 taste sea 4 Unitarity? (same disease as quenched) 4 Which are the physical valence states? Algorithms for Lattice QCD 10

Why Fat Links? 4 Construct good sources & sinks 4 Better overlap with ground state 4 Spatial smearing 4 Suppress UV fluctuations 4 Improved actions for dynamical computations Algorithms for Lattice QCD 11

Fat Links: Buyer’s Guide 4 DBW 2 4 HYP 4 APE 4 Stout 4 FLIC 4 Lüscher-Weiss 4 Iwasaki 4 Symanzik Algorithms for Lattice QCD 12

Fat Links: Dynamical FLIC 4 Molecular dynamics with fat links 4 Fat links appear to work better when projected back onto the SU(3) group manifold 4 Let V be the usual APE smeared link 4 Iterative projection to U satisfying is not differentiable 4 Define instead 4 This is now (almost) differentiable 4 W Kamleh, D B Leinweber & A G Williams hep-lat/0403019 Algorithms for Lattice QCD 13

Stout Links 4 Even more differentiable 4 Let V be a suitably smeared link 4 Define , where T means the traceless antihermitian part (i. e. , projection onto the Lie algebra) 4 This is now differentiable 4 But it does not look too much like projection (except for ) 4 C Morningstar & M Peardon hep-lat/0311018 Algorithms for Lattice QCD 14

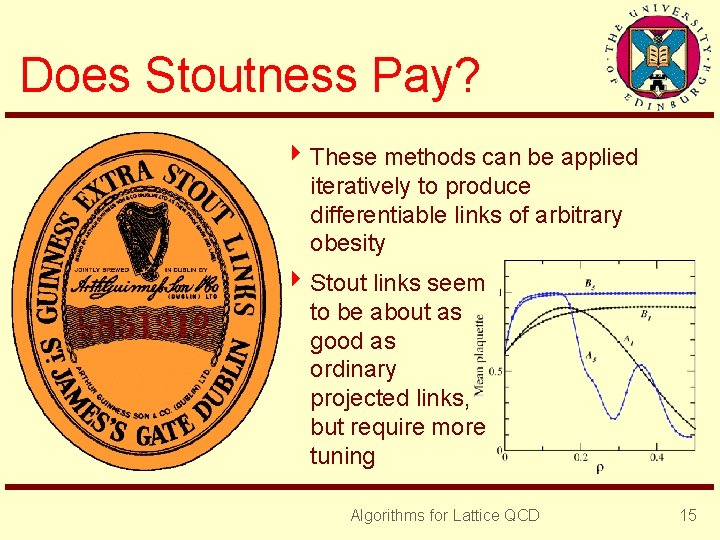
Does Stoutness Pay? 4 These methods can be applied iteratively to produce differentiable links of arbitrary obesity 4 Stout links seem to be about as good as ordinary projected links, but require more tuning Algorithms for Lattice QCD 15

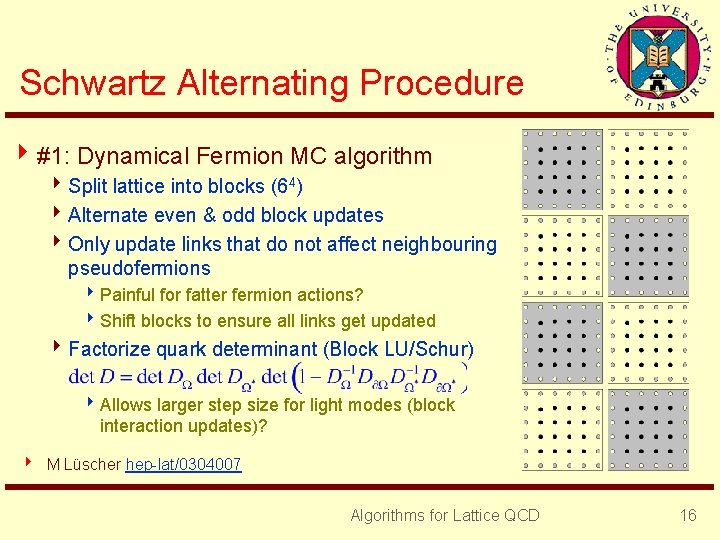
Schwartz Alternating Procedure 4 #1: Dynamical Fermion MC algorithm 4 Split lattice into blocks (64) 4 Alternate even & odd block updates 4 Only update links that do not affect neighbouring pseudofermions 8 Painful for fatter fermion actions? 8 Shift blocks to ensure all links get updated 4 Factorize quark determinant (Block LU/Schur) 8 Allows larger step size for light modes (block interaction updates)? 4 M Lüscher hep-lat/0304007 Algorithms for Lattice QCD 16

SAP Preconditioner 4#2: Preconditioner for linear solver 4 Use GCR or FGMRES solver 4 Accurate block solves not required 84 block MR steps, 5 Schwarz cycles 4 Parallelises easily 8 Especially on coarse-grained architectures such as PC clusters 4 Reduces condition number by preconditioning high frequency modes 4 M Lüscher hep-lat/0310048 Algorithms for Lattice QCD 17

R Algorithm 4 Inexact algorithm 4 Distribution has errors of O( 2) 4 Clever combination of nonreversibility and area nonpreservation 4 Asymptotic expansion in 4 Results for large do not just correspond to a renormalisation of the parameters 4 C. f. , perturbation theory is also asymptotic (or worse) 4 C. f. , “improvement” expansion in the cut-off a (lattice spacing) is also asymptotic 8 Scaling for highly-improved theories breaks down at smaller values of a 4 independent of volume 4 But probably so for HMC too, because of instability 4 S Gottlieb, W Liu, D Toussaint, R Renken, & R Sugar Phys. Rev. D 35: 2531 -2542, 1987 Algorithms for Lattice QCD 18

PHMC and RHMC 4 Use polynomial or rational function approximation for action 4 Approximate action suffices for MD 4 Accurate action need for acceptance 4 Functions on matrices 4 Defined for a Hermitian matrix by diagonalisation 4 H = UDU -1 4 f(H) = f(UDU -1) = U f(D)U -1 4 Polynomials and rational functions do not require diagonalisation 4 Hm + Hn = U( Dm + Dn) U -1 4 H -1 = U D -1 U – 1 4 T Takaishi & Ph de Forcrand hep-lat/9608093 4 R Frezzotti & K Jansen hep-lat/9702016 4 A D Kennedy, I Horváth, & S Sint hep-lat/9809092 4 M Clark & A D Kennedy hep-lat/0309084 Algorithms for Lattice QCD 19

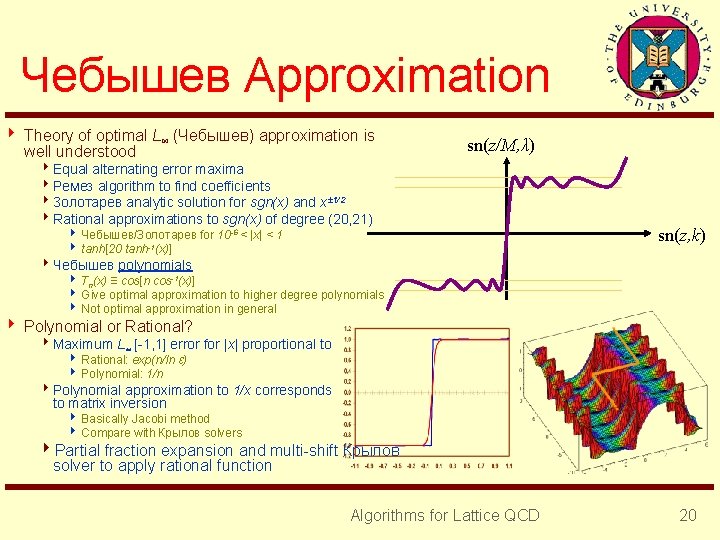
Чебышев Approximation 4 Theory of optimal L∞ (Чебышев) approximation is well understood sn(z/M, λ) 4 Equal alternating error maxima 4 Ремез algorithm to find coefficients 4 Золотарев analytic solution for sgn(x) and x± 1/2 4 Rational approximations to sgn(x) of degree (20, 21) 8 Чебышев/Золотарев for 10 -6 < |x| < 1 8 tanh[20 tanh-1(x)] sn(z, k) 4 Чебышев polynomials 8 Tn(x) ≡ cos[n cos-1(x)] 8 Give optimal approximation to higher degree polynomials 8 Not optimal approximation in general 4 Polynomial or Rational? 4 Maximum L∞ [-1, 1] error for |x| proportional to 8 Rational: exp(n/ln ε) 8 Polynomial: 1/n 4 Polynomial approximation to 1/x corresponds to matrix inversion 8 Basically Jacobi method 8 Compare with Крылов solvers 4 Partial fraction expansion and multi-shift Крылов solver to apply rational function Algorithms for Lattice QCD 20

Instability of Symplectic Integrators 4 Symmetric symplectic integrator 4 Leapfrog 8 Exactly reversible… 8…up to rounding errors 4 Ляпунов exponent 4 >0 8 Chaotic equations of motion 8 when exceeds critical value c 8 Instability of integrator 4 c depends on quark mass 4 4 4 C Liu, A Jaster, & K Jansen hep-lat/9708017 R Edwards, I Horváth, & A D Kennedy hep-lat/9606004 B Joó et al. (UKQCD) hep-lat/0005023 Algorithms for Lattice QCD 21

Multipseudofermions 4 We want to evaluate a functional integral including the fermionic determinant det M 4 We write this as a bosonic functional integral over a pseudofermion field with kernel M-1: 4 We are introducing extra noise into the system by using a single pseudofermion field to sample this functional integral 4 This noise manifests itself as fluctuations in the force exerted by the pseudofermions on the gauge fields 4 This increases the maximum fermion force 4 This triggers the integrator instability 4 This requires decreasing the integration step size 4 A better estimate is det M = [det M 1/n]n 4 Algorithms for Lattice QCD 22

Reduction of Maximum Force 4 Hasenbusch trick 4 Wilson fermion action M=1 - H 4 Introduce the quantity M’=1 - ’H 4 Use the identity M = M’(M’-1 M) 4 Write the fermion determinant as det M = det M’ det (M’-1 M) 4 Separate pseudofermion for each determinant 4 Tune ’ to minimise the cost 4 Easily generalises 4 More than two pseudofermions 4 Wilson-clover action 4 M Hasenbusch hep-lat/0107019 Algorithms for Lattice QCD 23

RHMC Force Reduction 4 Use RHMC technique to implement nth root for multipseudofermions 4 Use partial fractions & multishift for nth root 4 No tuning required 4 Cost proportional to condition number (M) 4 Maximum force reduction 4 Condition number (r(M))= (M)1/n 4 Force reduced by factor n (M)(1/n)-1 4 Increase step size to instability again 4 Cost reduced by a factor of n (M)(1/n)-1 4 Optimal value nopt ln (M) 4 So optimal cost reduction is (e ln ) / 4 Cannot reduce exact (mean) force 4 A D Kennedy & M Clark Algorithms for Lattice QCD 24

Reducing δH fluctuations 4 If 4 Follow trajectory U 0 →U 2 with step size δτ/2 4 If probability accept U 2 with 4 Otherwise reject (stay at U 0) 4 How much does this help if we are hitting the integrator instability? 4 Things only get worse if we are not yet in equilibrium 4 M Lüscher & R Sommer Algorithms for Lattice QCD 25

Old Integrator Tricks 4 Sexton-Weingarten 4 Split MD Hamiltonian into parts 8 Boson and fermion actions 4 Construct symmetric symplectic integrator with larger steps for more expensive (fermion) part 8 Use BCH formula 4 Helps if step size limited by cheaper (boson) part 4 Unfortunately, becomes less useful as m. Q → 0 4 D Weingarten & J Sexton Nucl. Phys. Proc. Suppl. 26, 613 -616 (1992) Algorithms for Lattice QCD 26

Dynamical Chiral Fermions 4 Conventions 4 We shall work in Euclidean space with Hermitian matrices 4 We shall write 4 We shall take all Dirac operators to be 5 Hermitian Algorithms for Lattice QCD 27

On-shell chiral symmetry 4 Is it possible to have chiral symmetry on the lattice without doublers if we only insist that the symmetry holds on shell? 4 Such a transformation should be of the form (Lüscher) 4 For it to be a symmetry the Dirac operator must be invariant 4 For a small transformation this implies that 4 Which is the Ginsparg-Wilson relation Algorithms for Lattice QCD 28

Neuberger’s operator: I 4 We can find a solution of the Ginsparg-Wilson relation as follows 4 Let the lattice Dirac operator to be of the form 4 This satisfies the GW relation if 4 And it must also have the correct continuum limit 4 Both of these conditions are satisfied if we define (Neuberger) Algorithms for Lattice QCD 29

Neuberger’s operator: II 4 There are many other possible solutions 4 Use another Dirac operator within Neuberger’s operator 4 The discontinuity is necessary 4 We are only considering vector-like theories 4 Chiral theories with unpaired Weyl fermions can be discretised on the lattice, but getting the phase of the fermion measure correct is critical 4 Simulating such theories is a much harder problem Algorithms for Lattice QCD 30

Into Five Dimensions 4 5 D formulation of overlap 4 Continued fraction representation 4 Relation between Domain Wall & Overlap formulations 4 Gauge fields are only four dimensional 4 Construct fifth dimensional transfer matrix T 4 Integrate out bulk pseudofermion fields 8 Jacobian cancelled by Pauli-Villars fields 4 Construct effective four dimensional Hamiltonian (Cayley transform) 4 Gives Higham approximation to Neuberger operator 4 Truncated Overlap for which 4 Optimal Domain Wall using Золотарев approximation 4 4 4 H Neuberger hep-lat/9806025 A Boriçi, A D Kennedy, B Pendleton, U Wenger hep-lat/0110070 A Boriçi hep-lat/9909057, hep-lat/9912040, hep-lat/0402035 R Edwards & U Heller hep-lat/0005002 T-W Chiu hep-lat/0209153 , hep-lat/0211032, hep-lat/0303008 Algorithms for Lattice QCD 31

Overlap Algorithms 4 many formulations of overlap fermions 4 All satisfy GW relation 4 Equivalent in continuum limit 8 Different lattice Dirac operators within sgn function 8 Different approximations to sgn function 8 Presumably also true for perfect actions 4 Trade-off between speed and amount of chirality 4 Choice of inversion algorithm 8 Inner-outer Krylov iterations 8 Various five dimensional formulations 8 Several possible preconditioners Algorithms for Lattice QCD 32

Dynamical Overlap 4 Fodor, Katz, & Szabó: dynamical overlap on ridiculously small lattices 4 Reflection & refraction 4 Brower, Originos, & Neff: Interpolate between DW & Truncated Overlap 4 Topology change in chiral limit? 4 van der Eshof et al. : Preconditioners, flexible inverters 4 NIC/DESY: Inverter tests for QCD™ & overlap 4 Z Fodor, S Katz, and K Szabó hep-lat/0311010 4 R Brower, K Originos, & H Neff 4 van der Eshof et al. hep-lat/0202025, hep-lat/0311025, hep-lat/0405003 Algorithms for Lattice QCD 33

Other Topics 4 Keh-Fei Liu & Andrei Alexandru 4 Noisy non-vanishing baryon number density on tiny lattices 4 Shailesh Chandrasekharan 4 Strong coupling algorithm for QCD 8 Strong coupling, but chiral limit Algorithms for Lattice QCD 34

The Future: Faster Monte Carlo Algorithms for Lattice QCD 35