Workshop on Dynamical Systems and Computation Dynamical Systems

Workshop on Dynamical Systems and Computation Dynamical Systems for Extreme Eigenspace Computations Maziar Nikpour UCL Belgium 1

Workshop on Dynamical Systems and Computation Co-workers Iven M. Y. Mareels Jonathan H. Manton University of Melbourne, Australia. Vadym Adamyan Odessa State University, Ukraine. Uwe Helmke University of Wurzberg, Germany. 2

Problem Workshop on Dynamical Systems and Computation • For Hermitian matrices (A, B), with B > 0; find the non-trivial solutions (l, x) of with the smallest or largest generalised eigenvalues l. n – size of matrices (A, B) k – no. of desired generalised eigenvalue/eigenvector pairs. 3

Workshop on Dynamical Systems and Computation Outline • Introduction • Motivation • Brief history of literature • • • Penalty function approach Gradient flow Convergence Discrete-time Algorithms Applications Conclusions 4

Workshop on Dynamical Systems and Computation Motivation • Signal Processing • Telecommunications • Control • Many others… 5

Brief History of Problem • Numerical Linear Algebra Literature Workshop on Dynamical Systems and Computation – Methods for general A and B: • QZ algorithm, Moler and Stewart 1973. (what MATLAB does when you type ‘eig’) – Methods for large and sparse A, B. • Trace minimisation method, Sameh & Wisiniewski, 1981. • Engineering Literature • Methods largely for computing largest/smallest generalised evs adaptively • Mathew and Reddy 1998 (inflation approach, special case of approach in this work). • Strobach, 2000 (tracking algorithms). 6

Brief History of Problem • Dynamical systems literature Workshop on Dynamical Systems and Computation – Brockett flow – Oja • Above approaches cannot be adapted to the Generalised Eigenvalue problem without manipulating A and/or B. • Recent paper by Manton et al. presents an approach that can… 7

Penalty Function Approach Workshop on Dynamical Systems and Computation • The minimisation of the following cost can lead to algorithms for computing extreme generalised evs. 8

Dynamical Systems for Numerical Computations Workshop on Dynamical Systems and Computation Gradient descent like flows on a cost function. Discretisation of flows. Efficient numerical algorithms. 9

Examples Workshop on Dynamical Systems and Computation • Power flow: • Oja subspace flow: • Brockett flow: 10

Contributions Workshop on Dynamical Systems and Computation • Gradient flow on f(A, B) • Discretisation of Gradient Flow – Steepest Descent – Conjugate Gradient • Stochastic minor/principal component tracking algorithms • The case B = I, and Z real has already been treated. (see Manton et al. 2003). Extending the domain to the complex matrices complicates the analysis substantially… Allowing B to be any p. d. matrix expands the range of applications… 11

Gradient Flow Workshop on Dynamical Systems and Computation • Main Result: For almost all initial conditions, solutions of converge to a single point in the stable invariant set of the flow. 12

Gradient Flow Workshop on Dynamical Systems and Computation • The stable invariant set is: 13

Critical Points of f(A, B) Workshop on Dynamical Systems and Computation • Hessian of f(A, B) is degenerate at critical points, N. B. • Proposition: 14

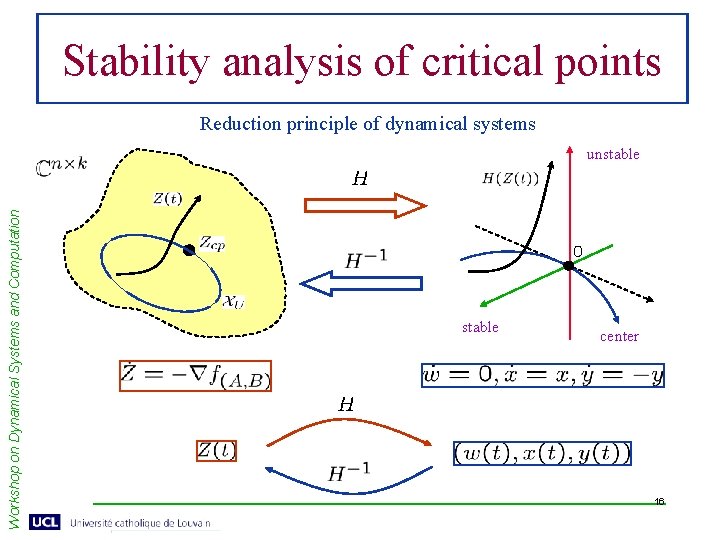
Workshop on Dynamical Systems and Computation Stability analysis of critical points • Linear stability analysis will not suffice. • Use center manifold theorem at each c. p. • Proposition: Why? Nullspace of hessian of cost func. = Tangent space of critical subman. 15

Stability analysis of critical points Reduction principle of dynamical systems Workshop on Dynamical Systems and Computation unstable center 16

Workshop on Dynamical Systems and Computation Stability analysis of critical points • Main result follows…. • Proposition: level sets are compact => flow converges to one of the critical components. • Center manifold thm. + reduction principle => converge to a single point on a critical component. • Converges to stable invariant set for an open dense set of initial conditions. 17

Workshop on Dynamical Systems and Computation Remarks • Conditions used in proof => f(A, B) is a Morse-Bott function => solutions converge to a single point instead of a set (see Helmke & Moore, 1994). • Also f(A, B) is a real analytic function (Cn x k considered as a real vector space) => convergence to a single point (Lojasiewicz, 1984). 18

Further Remarks Workshop on Dynamical Systems and Computation • Generalised eigenvectors not unique but convergence to particular g. evs can be achieved by the following flow in reduced dimensions: where trunc{X} denotes X with imaginary components of diagonal set to 0. Flow converges to an element of critical component with real diagonal elements. 19

Systems of Flows Workshop on Dynamical Systems and Computation • Consider the system of cost functions: 20

Systems of Flows Workshop on Dynamical Systems and Computation • System of partial gradient descent flows allows the possibility to add or take away components without affecting the computation of others • Proposition: Z(t) converges to smallest generalised eigenvalues for a generic initial condition. 21

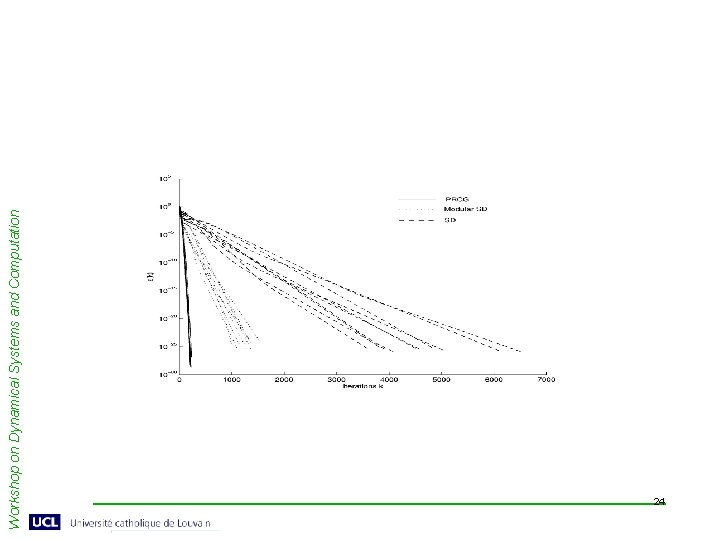
Discrete-time algorithms Workshop on Dynamical Systems and Computation • Since flow evolves on a Euclidean space – discretisation is not complicated: • Steepest descent: • Conjugate gradient 22

Workshop on Dynamical Systems and Computation Discrete-time algorithms • Can solve the Hermitian definite GEVP without any factorisation or manipulation of A or B. • Only matrix – small matrix multiplications are required. • Suitable for cases where A and B are large and sparse. • Conjugate gradient algorithm – superlinear convergence but no increase in order of computational complexity. • Complexity O(n 2 k). • Exact line search can be performed. 23

Workshop on Dynamical Systems and Computation 24

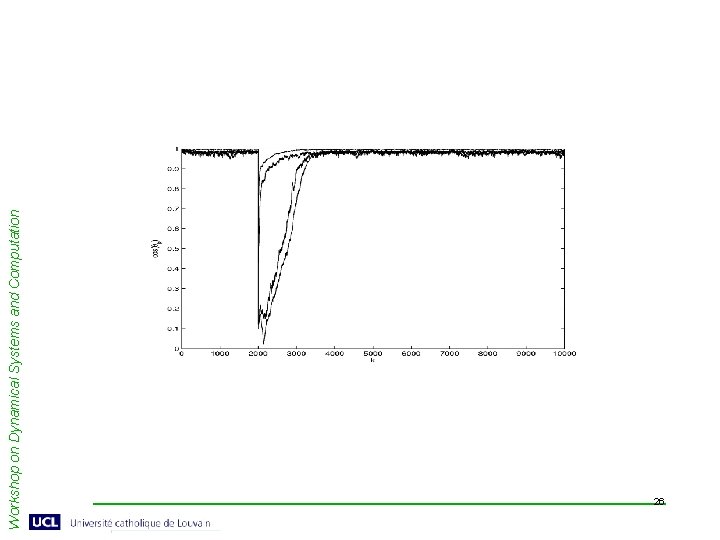
Discrete-time algorithms Workshop on Dynamical Systems and Computation • Tracking algorithm: - signal plus noise model • O(nk 2) complexity when Rnn = I. 25

Workshop on Dynamical Systems and Computation 26

Workshop on Dynamical Systems and Computation Conclusion • Proposing and deriving convergence theory of a gradient flow for solving GEVP. • Modular system of flows. • Discretisation: CG and SD algorithms. • Application to Minor component tracking. 27

Workshop on Dynamical Systems and Computation Questions 28