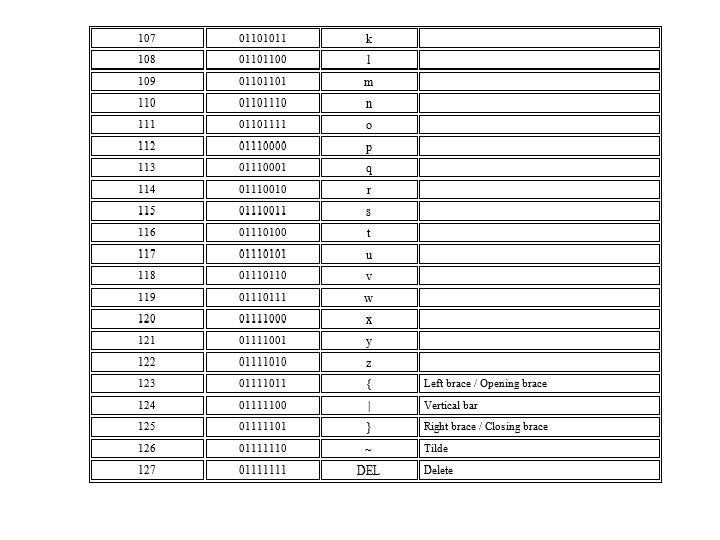
AES exercices AES Advanced Encryption Standard standard de


![Le groupe commutatif GF(28) Par définition, GF(28) = F 2[X] / P = Proposition: Le groupe commutatif GF(28) Par définition, GF(28) = F 2[X] / P = Proposition:](https://slidetodoc.com/presentation_image_h/2b744e2458061464de844b377ef463a7/image-3.jpg)


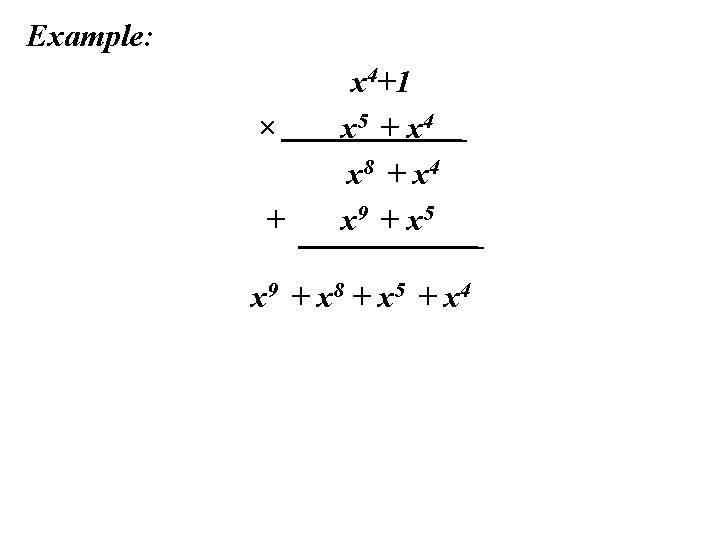






![• la matrice(Add. Roundkey[0]) St : = St ⊕ T. = 49 72 • la matrice(Add. Roundkey[0]) St : = St ⊕ T. = 49 72](https://slidetodoc.com/presentation_image_h/2b744e2458061464de844b377ef463a7/image-22.jpg)



- Slides: 29

AES exercices

AES (Advanced Encryption Standard ) « standard de chiffrement avancé » C’est un algorithme de chiffrement symétrique par bloc.
![Le groupe commutatif GF28 Par définition GF28 F 2X P Proposition Le groupe commutatif GF(28) Par définition, GF(28) = F 2[X] / P = Proposition:](https://slidetodoc.com/presentation_image_h/2b744e2458061464de844b377ef463a7/image-3.jpg)
Le groupe commutatif GF(28) Par définition, GF(28) = F 2[X] / P = Proposition: K[X]/P[X] est un corps si et seulement si P est irréductible dans K[X]

AES • L’addition = XOR • La multiplication = une multiplication modulo 11 B (x 8+x 4+x 3+x+1)

Multiplication in GF(28) Can be accomplished by first multiplying each term of the second polynomial with all of the terms of the first polynomial. Each of these products should be added together. If the degree of the new polynomial is greater than 7, then it must be reduced modulo some irreducible polynomial. In the case of AES, the irreducible polynomial is x 8+x 4+x 3+x+1
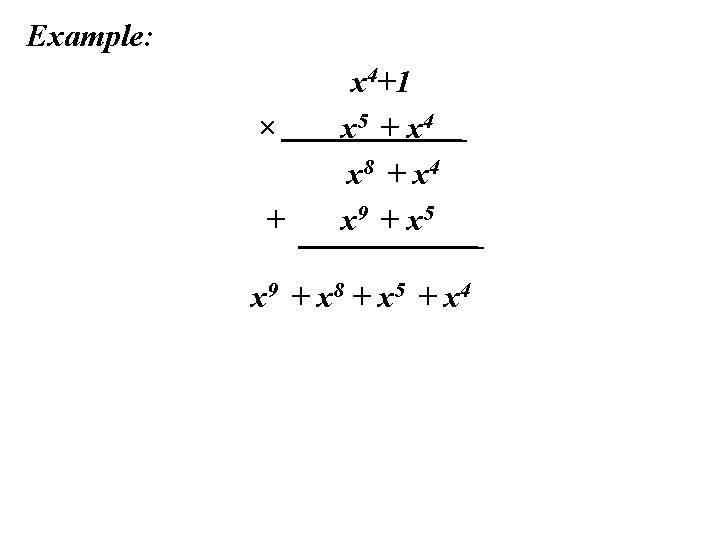
Example: × + x 4+1 x 5 + x 4 x 8 + x 4 x 9 + x 5 x 9 + x 8 + x 5 + x 4

x 9 + x 8 + x 5 + x 4 Since the degree of the result is greater than 7, then we must reduce it modulo x 8+x 4+x 3+x+1 This can be accomplished by multiplying the polynomial by xi− 8, where i is the degree of the polynomial that is to be reduced. In our example, we perform: x 9 + x 8 + x 5 + x 4 + x 9 + x 5 + x 4 + x 2 + x x 8 + x 2 + x 8+x 4+x 3+x+1 x 4+x 3+x 2+1

Therefore: × x 4+1 x 5 + x 4+x 3+x 2+1 Or: (0001)2 × (00110000)2 = (00011101)2 Or: (11)16 × (30)16 = (1 D)16

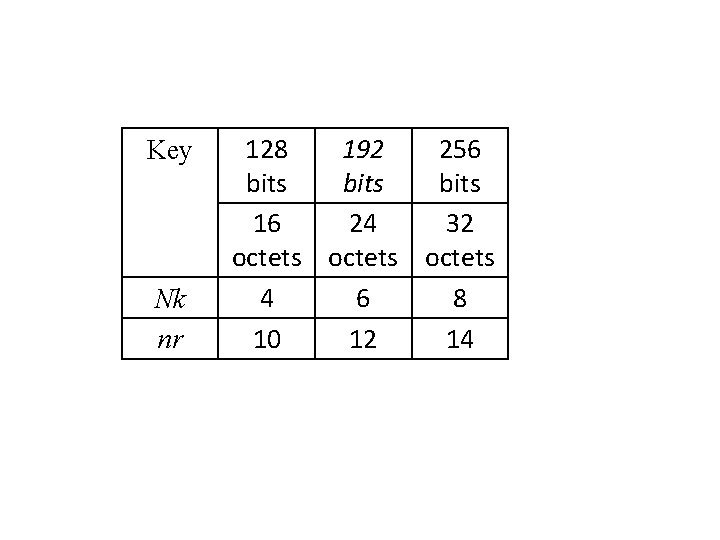
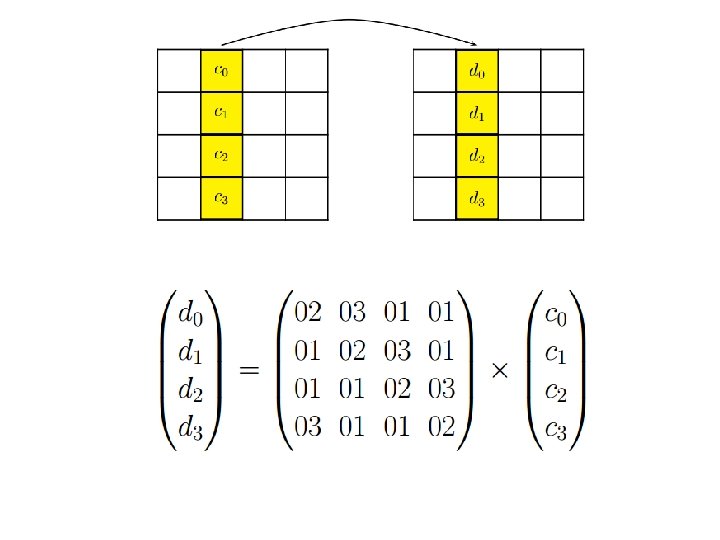
On découpes les données et les clés en octets et on les place dans des tableaux. Exemple:

Key Nk nr 128 192 256 bits 16 24 32 octets 4 6 8 10 12 14



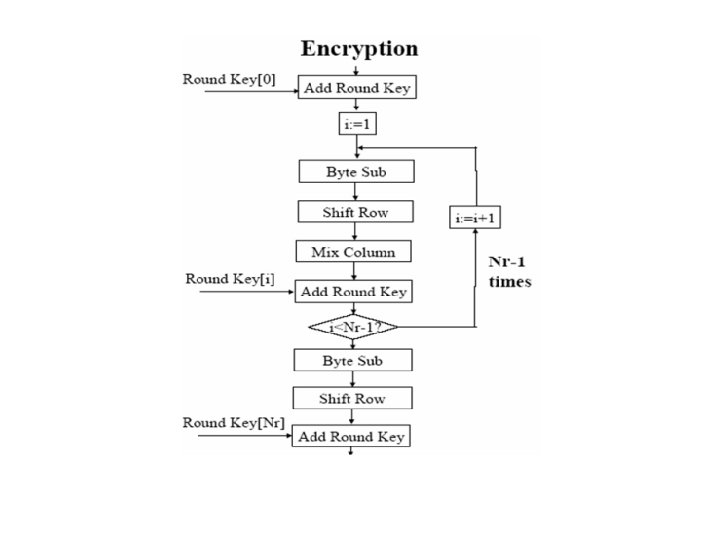
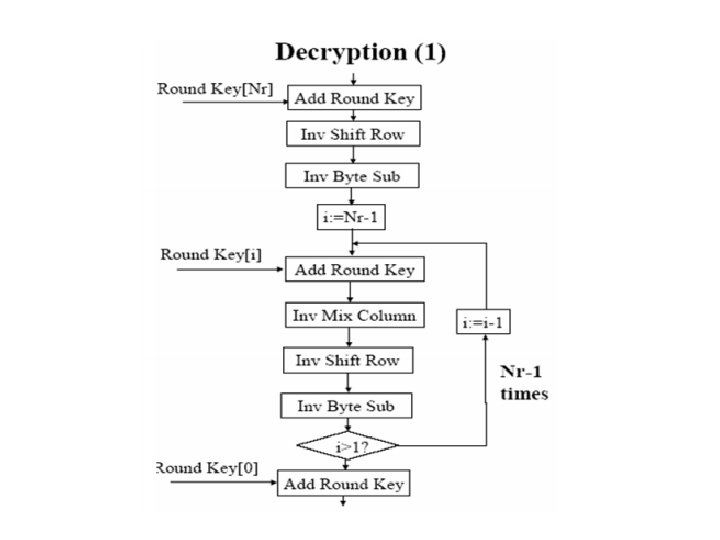
• Texte clair: Informatique GL. • Clé : Post-graduation( blanc) Calculer: la matrice(Add. Roundkey[0]) Pour Round 1: - la matrice Sub. Bytes. - la matrice Shift. Rows. - la première colonne de la matrice Mix. Colums.

Solution







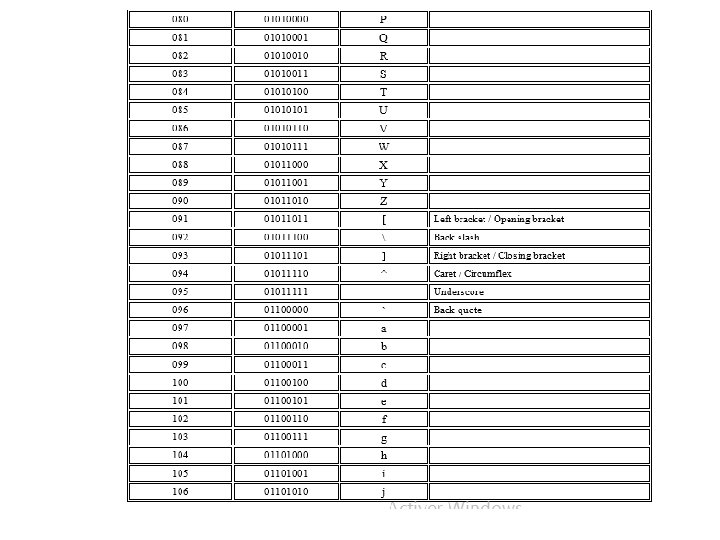
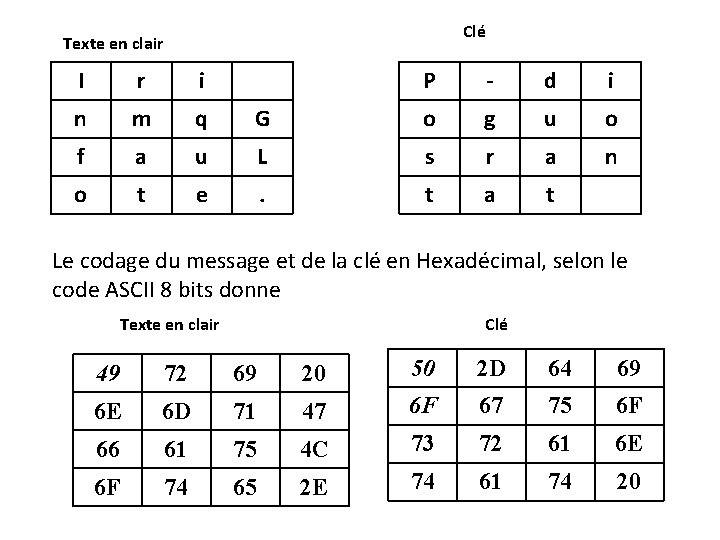
Clé Texte en clair I r i n m q f a o t P - d i G o g u o u L s r a n e . t a t Le codage du message et de la clé en Hexadécimal, selon le code ASCII 8 bits donne Texte en clair Clé 49 72 69 20 50 2 D 64 69 6 E 6 D 71 47 6 F 67 75 6 F 66 61 75 4 C 73 72 61 6 E 6 F 74 65 2 E 74 61 74 20
![la matriceAdd Roundkey0 St St T 49 72 • la matrice(Add. Roundkey[0]) St : = St ⊕ T. = 49 72](https://slidetodoc.com/presentation_image_h/2b744e2458061464de844b377ef463a7/image-22.jpg)
• la matrice(Add. Roundkey[0]) St : = St ⊕ T. = 49 72 69 20 50 2 D 64 69 6 E 6 D 71 47 6 F 67 75 6 F 66 61 75 4 C 73 72 61 6 E 6 F 74 65 2 E 74 61 74 20 ⊕ 19 5 F 0 D 49 01 0 A 04 28 15 13 14 22 1 B 15 11 0 E


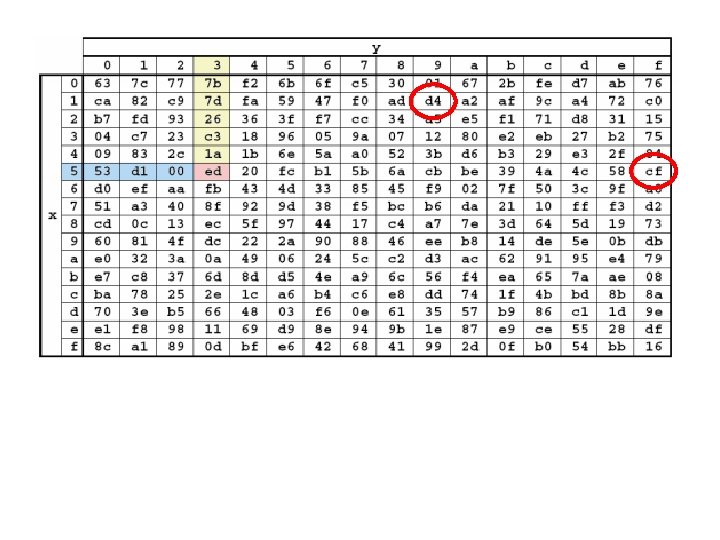
La matrice Sub. Bytes correspondante D 4 CF D 7 3 B 7 C 67 F 2 34 59 7 D FA 93 AF 59 82 AB

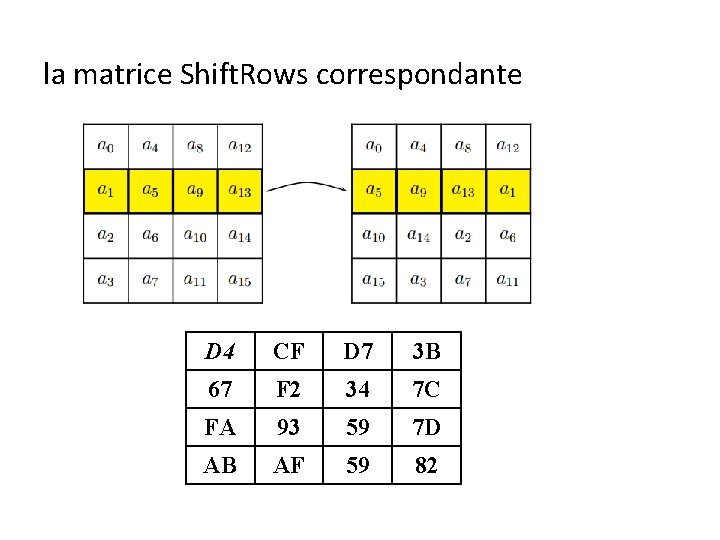
la matrice Shift. Rows correspondante D 4 CF D 7 3 B 67 F 2 34 7 C FA 93 59 7 D AB AF 59 82

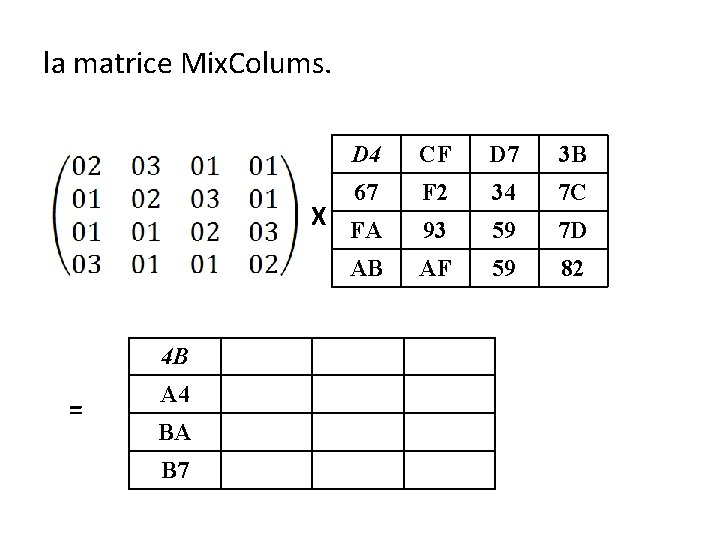
Mix. Columns


la matrice Mix. Colums. D 4 CF D 7 3 B 67 F 2 34 7 C 93 59 7 D AF 59 82 X FA AB {02. d 4} {03. 67} {01. fa} {01. ab} = 4 b

la matrice Mix. Colums. D 4 CF D 7 3 B 67 F 2 34 7 C 93 59 7 D AF 59 82 X FA AB 4 B = A 4 BA B 7