AES Advanced Encryption Standard Origins of AES In

AES Advanced Encryption Standard

Origins of AES • In 1999, NIST issued a new standard that is said 3 DES, – 168 -bit key length – Algorithm is the same as DES • 3 DES had drawbacks – Algorithm is sluggish in software – Only uses 64 -bit block size

Origins of AES (2) • In 1997, NIST issued a calls for proposals for the new Advanced Encryption Standard (AES) – security strength >= 3 DES – improved efficiency – must be a symmetric block cipher (128 -bit) – key lengths of 128, 192, and 256 bits

Evolution of AES • The Previous algorithms like DES were not secure enough after the inclusion of fastest computing technologies. • AES has key sizes of 128, 192 and 256 bits which were higher than that of previous one. • No method exists to break the AES key even if a key is found @ 1 second, it would still take 149 trillion years to crack the 128 -bit AES key.

AES Evaluation Criteria • Criteria used by NIST to evaluate potential candidates – Initial Criteria: • Security • Cost • Algorithm characteristics – Final Criteria: • General Security • Software Implementations • Restricted-space environments • Flexibility • Hardware Implementations • Attacks on Implementations • Encryption vs. Decryption • Key agility

Rounds of Evaluation • First round of evaluation – 15 proposed algorithms accepted • Second round – 5 proposed algorithms accepted • Final Standard - November 2001 – Rijndael selected as AES algorithm • Created by Dr. Joan Daemen and Dr. Vincent Rijmen

What makes Rijndael stand out? • The Symmetric and parallel structure • gives implementers a lot of flexibility • Has not allowed effective cryptanalytic attacks. • Well adapted to modern processors • Pentium • RISC and parallel processors • Suited for Smart cards • Flexible in dedicated hardware

AES Formation • AES uses Block Cipher technique • A block cipher is a type of symmetric-key encryption algorithm that transforms a fixed-length block of plaintext (unencrypted text) data into a block of Cipher text (encrypted text) data of the same length

AES Requirements • Symmetric Cipher • Block size must be at least 128 bits; keys of 128, 192 and 256 must be applicable. • It should resist to all known methods of cryptanalysis • No Propriety • Design simplicity • Speed and code Compactness on a wide range of platforms.

Expand Key Inverse shift rows Mix Columns Inverse mix cols w[4, 7] . . . Add round key Inverse sub bytes Inverse shift rows Substitute Bytes Round 9 Inverse sub bytes Shift Rows Add round key Shift Rows . . . Mix Columns Inverse mix cols Add Round Key Round 10 Add round key w[36, 39] Add round key Substitute Bytes Inverse sub bytes Shift Rows Inverse shift rows Add Round Key Ciphertext Round 9 Round 1 Substitute Bytes w[0, 3] w[40, 43] Add round key Ciphertext Round 1 Add round key Round 10 Plaintext

Basic Operations • • • The Rijndael Algorithm is a block cipher that encrypt blocks of 128, 192, or 256 bits. Uses symmetric keys of 128, 192 or 256 bits. It consists of an initial round (Add. Round. Key), and r standard rounds, r is 10, 12 or 14 depending on the block and key length. The first r-1 rounds are similar and they consist of 4 transformations, called – – Byte. Sub (Substitution Bytes) Shift. Row (Shift Rows) Mix. Column (multiply columns) Add. Round. Key (XOR by key ) The last round have only the transformations – Byte. Sub – Shift. Row – Add. Round. Key

Details Terms used

Algorithm Parameters, Symbols, and Functions

Working of Algorithm • The number of rounds for the algorithm depends on the key length and Block size.

Building Blocks • Key schedule to provide K[r]. – Key scheduling is to generate the subkeys K[r]. • Encryption (10 rounds in 128 bits case) – Transformation of plain text to cipher text.

Illustration by Example • Consider Matrix B[ji] which is B[00] B[01] B[02] B[03] B[10] B[11] B[12] B[13] B[20] B[21] B[22] B[23] B[30] B[31] B[32] B[33] In the 192 bits case, we have to add 2 columns more In the 256 bits case, we have to add 4 columns more All transformations are applied to B, except Add. Round. Key(B, Kr), it has another input, the sub-key K[r][ji]. The sub-keys K[r] that it generates are loaded in a linear array W. The lenght of the array W depend on the block and key length, it provides the sub-keys K[r] to every round r.

• Plain Text – B = 000102030405060708090 A 0 B 0 C 0 D 0 E 0 F • Key – K = 000102030405060708090 A 0 B 0 C 0 D 0 E 0 F

Key Schedule • The key schedule is used to provide the sub-keys K[r] • Beginning with the key K, we extend it (called Key Expansion), and get the linear array W. W is an array with 4 -byte words [Nb*(Nr+1)], where Nb is the number of columns of the matrix B[i, j], and Nr is the number of rounds. Here Nb=4, Nr=10, so W have [4*(10+1)] = 44 words of 32 b. • Every block of 4 words have 128 b and it is the sub-key [r]. • The first sub-key is K[0] = (W[0], W[1], W[2], W[3]), which is the copy of the key K • The next sub-keys are derived from the K[0]. The rule is

Rule to Derive the Sub-Keys W[4] = W[0] xor temp 1 W[5] = W[1] xor W[4] W[6] = W[2] xor W[5] where i mod Nk <> 0, the rule is: W[7] = W[3] xor W[6] W [i] = W[i-Nk] xor W[i-1], W[8] = W[4] xor temp 2 with Nr=4. . where i mod Nk = 0, we have W[42] = W[38] xor W[41] W[i] = W[i-Nk] xor tempk, where W[43] = W[39] xor W[42] tempk = Sub. Byte[Shift(1)(W[i-1])] xor rcon[k] Sub. Byte is applied to W[i-1] with a byte shifted, and rcon[k], is defined as rcon[k] = (RC[k], 00, 00), with RC[1] =1, and RC[k] = X*RC[k-1] = X^(k-1), are elements in GF(2^8). k = i/Nk, i = 4, 8, 12, . . . , 44 and Nk=4

Round Constant Word Array rcon[k] • • • Rcon[1]=[01, 00, 00] Rcon[2]=[02, 00, 00] Rcon[3]=[04, 00, 00] Rcon[4]=[08, 00, 00] Rcon[5]=[10, 00, 00] • • • Rcon[6]=[20, 00, 00] Rcon[7]=[40, 00, 00] Rcon[8]=[80, 00, 00] Rcon[9]=[1 B, 00, 00] Rcon[10]=[36, 00, 00]

The Sub-Key K[0] • 00 04 08 0 C • 01 05 09 0 D • 02 06 0 A 0 E • 03 07 0 B 0 F

Evaluation of W[i] • When i is multiple of 4 The rule is W[i] = W[i-4] xor Sub. Byte[Shift(1)(W[i-1])] xor rcon[k] W[4] = W[0] xor Sub. Byte(S(1)(W[3])) D 6 = 00 AA = 01 74 = 02 FD = 03 xor D 7 xor AB xor 76 xor FE W[4][0] = W[4][0] xor rcon[1] D 6 = D 7 xor 02

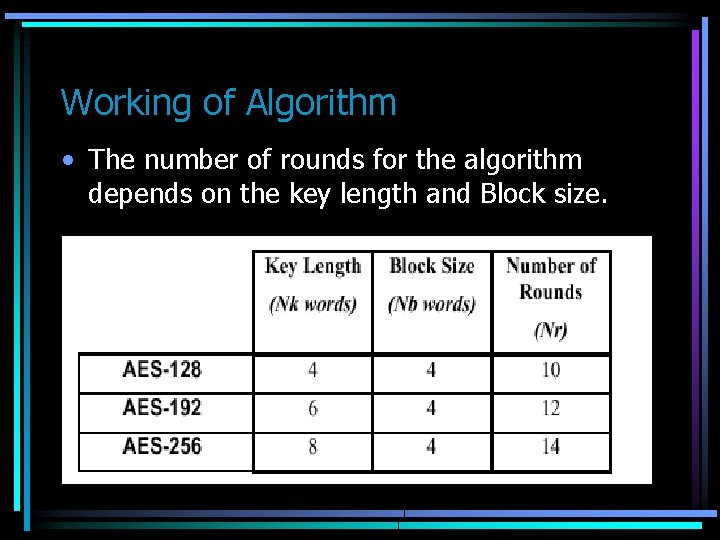
Determination of Sub. Byte Values • The S-box used in the Sub. Bytes() transformation is presented in hexadecimal form in next Figure • For example, for {53} then the substitution value would be determined by the intersection of the row with index ‘ 5’ and the column with index ‘ 3’ in Figure. This would result in a value of {ED}.

Sub. Bytes Transformation

Evaluation of W[i] • When i is not a multiple of 4 The rule is W[i] = W[i-4] xor W[i-1] W[5] = W[1] xor W[4] W[6] = W[2] xor W[5] W[7] = W[3] xor W[6] D 2 = 04 xor D 6 DA = 08 xor D 2 D 6 = 0 C xor DA AF = 05 xor AA A 6 = 09 xor AF AB = 0 D xor A 6 72 = 06 xor 74 78 = 0 A xor 72 76 = 0 E xor 78 FA = 07 xor FD F 1 = 0 B xor FA FE = 0 F xor F 1

Sub-Key K[1] • D 6 AA 74 FD D 2 AF 72 FA DA A 6 78 F 1 D 6 AB 76 FE

Home Work • Find All Remaining Sub-Keys

Remaining Keys • • • Sub-Key Sub-Key Sub-Key K[1] = D 6 AA 74 FD D 2 AF 72 FA DA A 6 78 F 1 D 6 AB 76 FE K[2] = B 6 92 CF 0 B 64 3 D BD F 1 BE 9 B C 5 00 68 30 B 3 FE K[3] = B 6 FF 74 4 E D 2 C 9 BF 6 C 59 0 C BF 04 69 BF 41 K[4] = 47 F 7 BC 95 35 3 E 03 F 9 6 C 32 BC FD 05 8 D FD K[5] = 3 C AA A 3 E 8 A 9 9 F 9 D EB 50 F 3 AF 57 AD F 6 22 AA K[6] = 5 E 39 0 F 7 D F 7 A 6 92 96 A 7 55 3 D C 1 0 A A 3 1 F 6 B K[7] = 14 F 9 70 1 A E 3 5 F E 2 8 C 44 0 A DF 4 D 4 E A 9 C 0 26 K[8] = 47 43 87 35 A 4 1 C 65 B 9 E 0 16 BA F 4 AE BF 7 A D 2 K[9] = 54 99 32 D 1 F 0 85 57 68 10 93 ED 9 C BE 2 C 97 4 E K[10]= 13 11 1 D 7 F E 3 94 4 A 17 F 3 07 A 7 8 B 4 D 2 B 30 C 5

Encryption • Initial Round ( Key addition ) This transformation applies a XOR between every entry of matrices B[j, i] and K[0][j, i], i. e. B[j, i] = B[j, i] XOR K[0][j, i] B[j, i] 00 04 08 0 C 00 00 01 05 09 0 D 00 00 XOR = 02 06 0 A 0 E 00 00 03 07 0 B 0 F 00 00

Round 1 ( Byte Substitution) • This transformation replaces every entry of the input B[j, i] by the result of two operations • The first operation maps entries to their multiplicative inverse in GF(28). Every entry (a byte) has a polynomial representation with the irreducible polynomial f(x)=x 8+x 4+x 3+x+1 • The zero is mapped to zero.

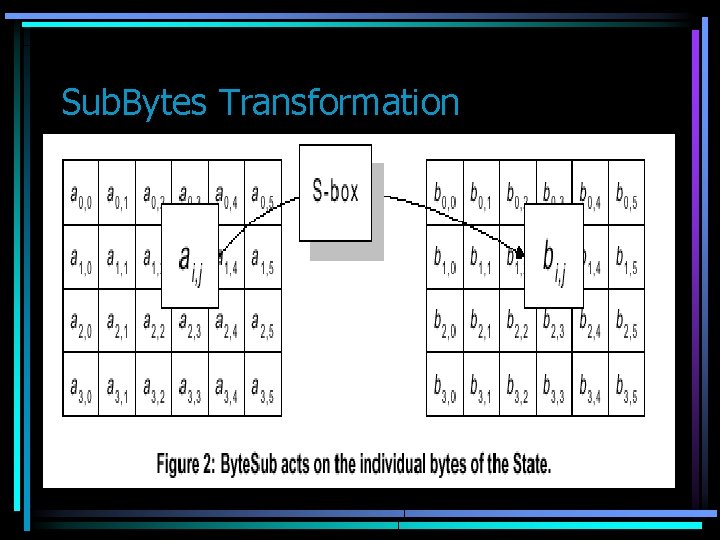
• • • Linear Transformation LT Here is the calculation for the entry (3, 3), LT(a[3, 3] -1) |y 0| |10001111||0| |1| |y 1| |11000111||0| |1| |y 2| |11100011||0| |y 3| |11110001||0| LT(a[j, i]-1) = |y 4|= |11111000||0|+|0| |y 5| |01111100||0| |1| |y 6| |00111110||0| |1| |y 7| |00011111||0| 63 63 63 63 | |___| The second operation applies a linear transformation from GF(2 8) to GF(28) for every entry (byte) of the matrix. The inputs are the bits x 7, . . , x 0 in a[j, i]-1 and the outputs are y 7, . . , y 0, this is the new element B[j, i] And this is the final output in the transformation Sub. Byte ( For Easiness refer to the same table used in key scheduling)

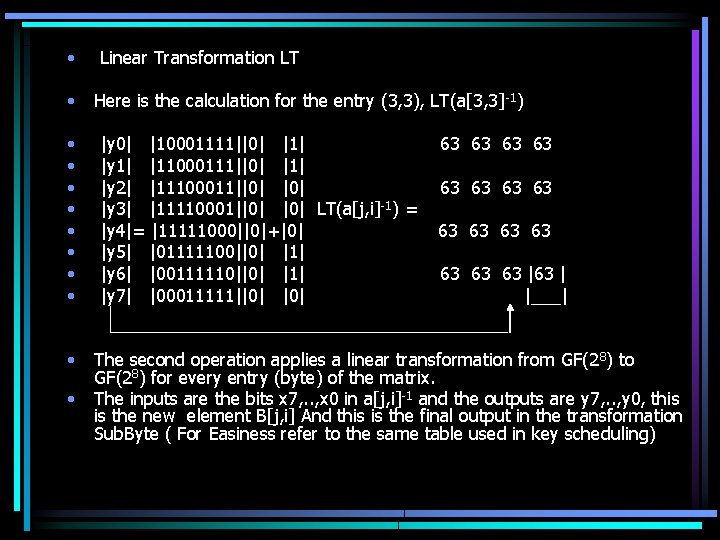
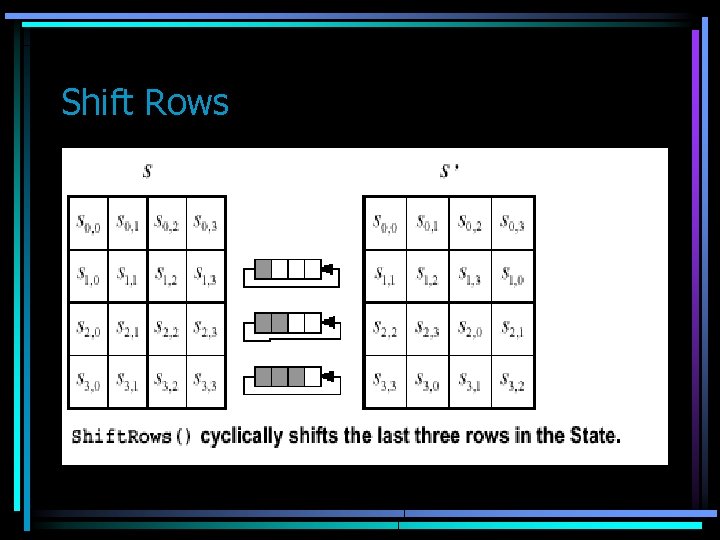
Shift Rows

• This transformation is applied to the rows of B[j, i], it shifts bytes in the rows. Row 1 is not shifted, row 2 is shifted 1 byte, row 3 shifted 2 bytes and row 4, 3 bytes (this is in our case of 128 b). In the case of 192 the same applies. In the case of 256 the only change is that rows 3 and 4 are shifted 3 and 4 bytes respectively.

63 63 63 Shift(a[j]) = 63 63 63 63 63 63

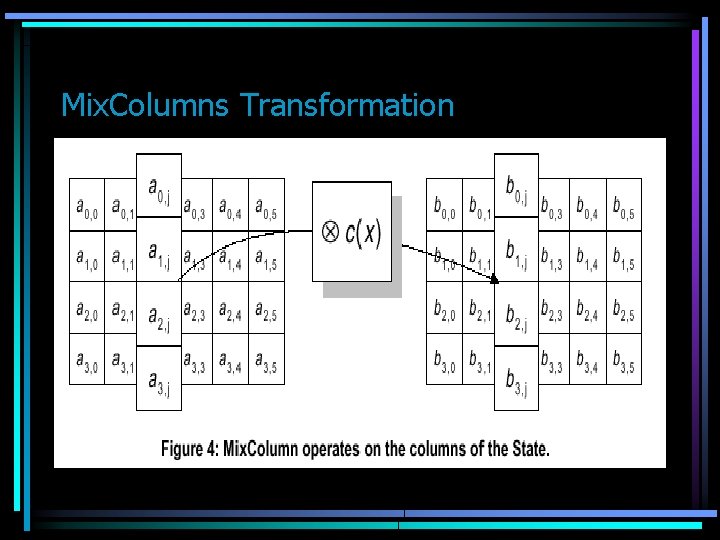
Mix Column • This transformation is applied to the columns of B[j, i], we can see each column as a polynomial of GF(28)[x] • So Mixcolumn multiplies each column by the constant polynomial c(x)=03 x 3 + 01 x 2 + 01 x + 02 • The coeficients are shown in hexadecimal, and they are in GF(28).

Mix. Columns Transformation

63 63 63 Mix. Colum(a[j]) = 63 63 63 63 63 63

Key Addition • This transformation only does an XOR between every entry the matrix B[j, i] and every entry of K[r][j, i] from the Key schedule. B[j, i] = B[j, i] XOR K[r][j, i]. • This is the final of the round r, and the partial vector test CT[r]

63 63 D 6 D 2 DA D 6 B 5 B 1 B 9 B 5 63 63 AA AF A 6 AB C 9 CC C 5 C 8 XOR = 63 63 74 72 78 76 17 11 1 B 15 63 63 FD FA F 1 FE 9 E 99 92 9 D

Cipher Text ( CT[1]) • B 5 C 9 17 9 E B 1 CC 11 99 B 9 C 5 1 B 92 B 5 C 8 15 9 D

Home Work • Do the remaining rounds by taking the CT[1] and apply the same steps. • The last round would not have any Mix Column transformation

Advantages • Implementation aspects: – Rijndael can be implemented to run at speeds unusually fast for a block cipher on a Pentium (Pro). There is a trade-off between table size/performance. – Rijndael can be implemented on a Smart Card in a small amount of code, using a small amount of RAM and taking a small number of cycles. There is some ROM/performance trade -off. – The round transformation is parallel by design, an important advantage in future processors and dedicated hardware. – As the cipher does not make use of arithmetic operations, it has no bias towards big or little endian processor architectures.

• Simplicity of Design: – The cipher is fully “self-supporting”. It does not make use of another cryptographic component, Sboxes “lent” from well-reputed ciphers, bits obtained from Rand tables, digits of p or any other such jokes. – The cipher does not base its security or part of it on obscure and not well understood interactions between arithmetic operations. – The tight cipher design does not leave enough room to hide a trapdoor.

• Variable block length: – The block lengths of 192 and 256 bits allow the construction of a collision-resistant iterated hash function using Rijndael as the compression function. The block length of 128 bits is not considered sufficient for this purpose nowadays. • Extensions: – The design allows the specification of variants with the block length and key length both ranging from 128 to 256 bits in steps of 32 bits. – Although the number of rounds of Rijndael is fixed in the specification, it can be modified as a parameter in case of security problems.

Limitations • The inverse cipher is less suited to be implemented on a smart card than the cipher itself: it takes more code and cycles. (Still, compared with other ciphers, even the inverse is very fast) • In software, the cipher and its inverse make use of different code and/or tables. • In hardware, the inverse cipher can only partially re-use the circuitry that implements the cipher.