1 27 301 MicrostructureProperties L 11 Tensors and

1 27 -301 Microstructure-Properties L 11: Tensors and Anisotropy, Part 4 Profs. A. D. Rollett, M. De Graef Processing Performance Microstructure Properties Last modified: 25 th Oct. ‘ 15 Please acknowledge Carnegie Mellon if you make public use of these slides

2 Objective • The objective of this lecture is to provide a mathematical framework for the description of properties, especially when they vary with direction. • A basic property that occurs in almost applications is elasticity. Although elastic response is linear for all practical purposes, it is often anisotropic (composites, textured polycrystals etc. ). Please acknowledge Carnegie Mellon if you make public use of these slides

3 1. 2. 3. 4. 5. Questions & Answers Why is it useful to rotate/transform the compliance tensor or matrix? Often we need to compute the elastic modulus in some particular direction that is not [100] or [111]. Why do we compute the compliance rather than the stiffness in the 1 -direction? This is subtle: we use compliance because one can impose a stress state that has only one non-zero component, from which we only need the strain component parallel to it. Poisson’s ratio tells us that imposing a strain in one direction automatically results in lateral strains (unless n=0), which means that it is not possible to have one and only one strain component contributing to a particular stress component. How are the quantities in the equation for the rotated/transformed s 11 related to the same equation with the Young’s moduli in the <100> and <111> directions? Comparison of the two formulae shows how to relate three S values to the Youngs’ moduli in the two directions. What is Zener’s anisotropy ratio? C' = (C 11 - C 12)/2; Zener’s ratio = C 44/C’. Which materials are most nearly isotropic? W at room temperature is almost isotropic and Al is not quite so close to being isotropic. How do we apply the equations to calculate the variation in Young’s modulus between [100] and [110] in a cubic metals such as Cu? Direction cosines are the quantities that are needed to define the direction in relation to the crystal axes. Please acknowledge Carnegie Mellon if you make public use of these slides

4 Q&A - 2 6. 7. 8. 9. What are the Lamé constants? These are the two constants l and G that are needed for isotropic elasticity. What do they have to do with isotropic elasticity? G has its usual meaning of shear modulus, or C 44: see the notes for how they relate to C 11 and C 12. How do they relate to Young’s modulus, bulk modulus and Poisson’s ratio? See the notes for the formulae. How do we write the piezoelectric matrix for quartz? 6 x 3 matrix. What stimuli and responses do each coefficient in the “d” matrix relate? Stimulus is the electric field and the response is the strain. What are the “BT” and “AT” cuts of a quartz crystal? These are cuts that maximize the usefulness of the thickness shear mode of oscillation. What equation describes the resonant frequency? See the notes. Why does temperature matter here? Temperature matters because one prefers to have a crystal that does not change its resonant frequency with temperature. Why does the density vary as the sum of 2 a 11+a 33? This sum is the trace of the matrix for the coefficient of thermal expansion, i. . e the variation in volume with change in T. How does the angle q relate to the AT and BT cuts already described? This angle is a rotation of the normal to the surface of the crystal in the y-z plane (i. e. rotation about x). How do we set up the equation that tells us the variation in d 66 with angle of cut? The Eq we need is that which describes the rate of change of resonant frequency with temperature. Please acknowledge Carnegie Mellon if you make public use of these slides

5 Rotated compliance (matrix) Given an orientation aij, we transform the compliance tensor, using cubic point group symmetry: Writing this out in full for the 1111 component: Re-writing this with vector-matrix notation gives: Please acknowledge Carnegie Mellon if you make public use of these slides

6 Rotated compliance (matrix) • This can be further simplified with the aid of the standard relations between the direction cosines, aikajk = 1 for i=j; aikajk = 0 for i¹j, (aikajk = ij) to read as follows: • By definition, the Young’s modulus in any direction is given by the reciprocal of the compliance, E = 1/S’ 11. • Thus the second term on the RHS is zero for <100> directions and, for C 44/C'>1, a maximum in <111> directions (conversely a minimum for C 44/C'<1). Please acknowledge Carnegie Mellon if you make public use of these slides

7 Anisotropy in terms of moduli • Another way to write the above equation is to insert the values for the Young's modulus in the soft and hard directions, assuming that the <100> are the most compliant direction(s). (Courtney uses a, b, and g in place of my a 1, a 2, and a 3. ) The advantage of this formula is that moduli in specific directions can be used directly. Please acknowledge Carnegie Mellon if you make public use of these slides

8 Cubic crystals: anisotropy factor • If one applies the symmetry elements of the cubic system, it turns out that only three independent coefficients remain: C 11, C 12 and C 44, (similar set for compliance). From these three, a useful combination of the first two is C' = (C 11 - C 12)/2 • See Nye, Physical Properties of Crystals Please acknowledge Carnegie Mellon if you make public use of these slides

9 Zener’s anisotropy factor • C' = (C 11 - C 12)/2 turns out to be the stiffness associated with a shear in a <110> direction on a {110} plane. In certain martensitic transformations, this modulus can approach zero which corresponds to a structural instability. Zener proposed a measure of elastic anisotropy based on the ratio C 44/C'. This turns out to be a useful criterion for identifying materials that are elastically anisotropic. Please acknowledge Carnegie Mellon if you make public use of these slides

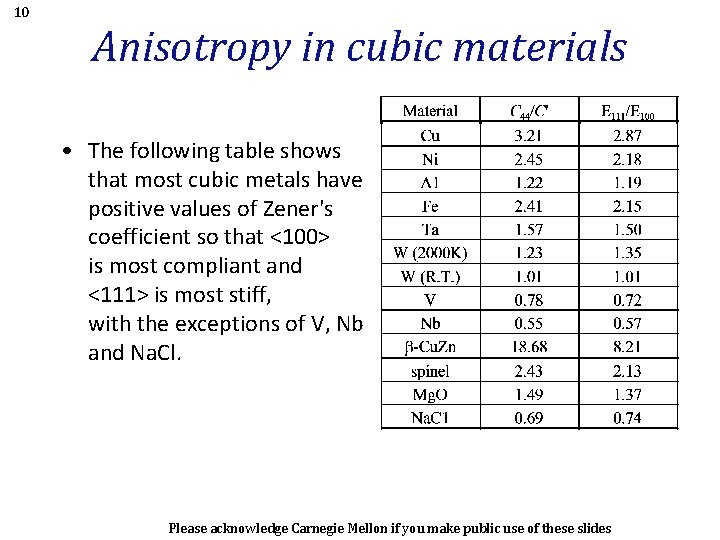
10 Anisotropy in cubic materials • The following table shows that most cubic metals have positive values of Zener's coefficient so that <100> is most compliant and <111> is most stiff, with the exceptions of V, Nb and Na. Cl. Please acknowledge Carnegie Mellon if you make public use of these slides

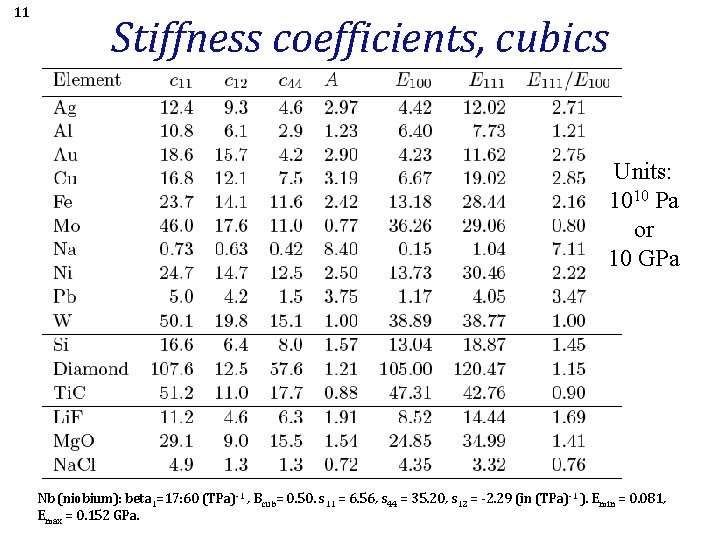
11 Stiffness coefficients, cubics Units: 1010 Pa or 10 GPa Nb (niobium): beta 1=17: 60 (TPa)-1 , Bcub= 0. 50. s 11 = 6. 56, s 44 = 35. 20, s 12 = -2. 29 (in (TPa)-1 ). Emin = 0. 081, Emax = 0. 152 GPa.

12 Example Problem [Courtney] Should be E<111>= 18. 89 Please acknowledge Carnegie Mellon if you make public use of these slides

13 Lamé constants (isotropic elasticity) For an elastically isotropic body, there are only 2 elastic moduli, known as the Lamé constants. Please acknowledge Carnegie Mellon if you make public use of these slides

14 Young’s, Bulk moduli, Poisson’s ratio Please acknowledge Carnegie Mellon if you make public use of these slides

15 Engineering with the Piezoelectric Effect • [Newnham, sections 12. 8 and 13. 10] The use of quartz as a resonant crystal for oscillator circuits with highly stable frequency depends strongly on the details of its properties. • Although quartz is only weakly piezoelectric, other aspects of its properties provide the key, namely thermal stability. • Most elastic stiffness coefficients have negative temperature coefficients, meaning that materials become less stiff with rising temperature. The c 66 coefficient of quartz, however, is positive; Table 13. 7. This offsets the effect of thermal expansion, which increases dimensions and decreases density. This is what makes it possible to have an oscillator that is insensitive to temperature changes. d 11 = 2. 27; d 14 =-0. 67 p. C/N http: //en. wikipedia. org/w iki/Electromagnetic_acous tic_transducer Please acknowledge Carnegie Mellon if you make public use of these slides

16 Quartz Oscillator Crystals, contd. • Resonant frequency, f, for thickness (t) shear mode, as a function of the rotation of axes to get c’ 66, where r is the density: • AT and BT cut modes are thickness shear modes driven by the piezoelectric coefficient d’ 26: e’ 6 = d’ 26 E’ 2 A particular angle must be determined for the ideal cut to minimize the temperature dependence of the resonant frequency. Please acknowledge Carnegie Mellon if you make public use of these slides

17 Quartz Oscillator Crystals, contd. • Temperature dependence of the resonant frequency, f, for thickness (t) shear mode, as a function of the rotation of axes to get c’ 66, where r is the density: • Temperature derivative of the thickness in the Z’ 2 (Y’) direction: • Transformed (rotated) stiffness coefficient: Please acknowledge Carnegie Mellon if you make public use of these slides

18 Quartz Oscillator Crystals, contd. • Quartz belongs to point group 23. Therefore c 1313 = c 55 = c 44 and c 1213 = c 65 = c 56 = c 14. • Taking the temperature derivative for c’ 66 and substituting all the relevant values into the equation, one obtains the following. Here, “T(c 66)” denotes the temperature coefficient of the relevant stiffness coefficient (Table 13. 7). The derivative of the resonant frequency, f, can be set equal to zero in the standard fashion in order to find the minima. • Applying the solution procedure yields two values with theta = -35° and +49°, corresponding to the two cuts illustrated. • Further discussion is provided by Newnham on how to make AC and BC cuts that are useful for transducers for transverselypolarized acoustic waves. Please acknowledge Carnegie Mellon if you make public use of these slides

19 Summary • We have covered the following topics: – Examples of elastic property values – Anisotropy coefficients (Zener) – Dependence of Young’s modulus on direction (in a crystal) – Worked example – Quartz oscillator crystals Please acknowledge Carnegie Mellon if you make public use of these slides

20 Supplemental Slides • The following slides contain some useful material for those who are not familiar with all the detailed mathematical methods of matrices, transformation of axes etc. Please acknowledge Carnegie Mellon if you make public use of these slides

21 Notation F R P j E D e s r d Stimulus (field) Response Property electric current electric field electric polarization Strain Stress (or conductivity) Resistivity piezoelectric tensor C elastic stiffness S elastic compliance a rotation matrix W work done (energy) I identity matrix O symmetry operator (matrix) Y Young’s modulus Kronecker delta e axis (unit) vector T tensor, or temperature direction cosine Please acknowledge Carnegie Mellon if you make public use of these slides

22 Bibliography • • • R. E. Newnham, Properties of Materials: Anisotropy, Symmetry, Structure, Oxford University Press, 2004, 620. 112 N 55 P. De Graef, M. , lecture notes for 27 -201. Nye, J. F. (1957). Physical Properties of Crystals. Oxford, Clarendon Press. Kocks, U. F. , C. Tomé & R. Wenk, Eds. (1998). Texture and Anisotropy, Cambridge University Press, Cambridge, UK. T. Courtney, Mechanical Behavior of Materials, Mc. Graw-Hill, 0 -07 -013265 -8, 620. 11292 C 86 M. Landolt, H. H. , Börnstein, R. , 1992. Numerical Data and Functional Relationships in Science and Technology, III/29/a. Second and Higher Order Elastic Constants. Springer. Verlag, Berlin. Zener, C. , 1960. Elasticity And Anelasticity Of Metals, The University of Chicago Press. Gurtin, M. E. , 1972. The linear theory of elasticity. Handbuch der Physik, Vol. VIa/2. Springer-Verlag, Berlin, pp. 1– 295. Huntington, H. B. , 1958. The elastic constants of crystals. Solid State Physics 7, 213– 351. Love, A. E. H. , 1944. A Treatise on the Mathematical Theory of Elasticity, 4 th Ed. , Dover, New York. Newey, C. and G. Weaver (1991). Materials Principles and Practice. Oxford, England, Butterworth-Heinemann. Reid, C. N. (1973). Deformation Geometry for Materials Scientists. Oxford, UK, Pergamon. Please acknowledge Carnegie Mellon if you make public use of these slides

23 Transformations of Stress & Strain Vectors • It is useful to be able to transform the axes of stress tensors when written in vector form (equation on the left). The table (right) is taken from Newnham’s book. In vector-matrix form, the transformations are: Please acknowledge Carnegie Mellon if you make public use of these slides