TENSORS 3 D STRESS STATE 1 Tensors Tensors

TENSORS/ 3 -D STRESS STATE 1

Tensors • Tensors are specified in the following manner: – A zero-rank tensor is specified by a sole component, independent of the system of reference (e. g. , mass, density). – A first-rank tensor is specified by three (3) components, each associated with one reference axis (e. g. , force). – A second-rank tensor is specified by nine (9) components, each associated simultaneously with two reference axes (e. g. , stress, strain). – A fourth-rank tensor is specified by 81 components, each associated simultaneously with four reference axes (e. g. , elastic stiffness, compliance). 2

• The Number of Components (N) required for the description of a TENSOR of the nth Rank in a k-dimensional space is: N = kn (4 -1) EXAMPLES (a) For a 2 -D space, only four components are required to describe a second rank tensor. (b) For a 3 -D space, the number of components N = 3 n Scalar quantities 30 Rank Zero Vector quantities 31 Rank One Stress, Strain 32 Rank Two Elastic Moduli 34 Rank Four 3

• The indicial (also called dummy suffix) notation will be used. • The number of indices (subscripts) associated with a tensor is equal to its rank. It is noted that: – density ( ) does not have a subscript – force has one (F 1, F 2, etc. ) – stress has two ( 12, 22, etc. ) • The easiest way of representing the components of a secondrank tensor is as a matrix • For the tensor T, we have: 4

The collection of stresses on an elemental volume of a body is called stress tensor, designated as ij. In tensor notation, this is expressed as: (4 -2) where i and j are iterated over x, y, and z, respectively. 5

• Here, two identical subscripts (e. g. , xx) indicate a normal stress, while a differing pair (e. g. , xy) indicate a shear stress. It is also possible to simplify the notation with normal stress designated by a single subscript and shear stresses denoted by , so: x xx xy (4 -3) 6

• In general, a property T that relates two vectors p = [p 1, p 2, p 3] and q = [q 1, q 2, q 3] in such a way that (4 -4) where T 11, T 12, ……. T 33 are constants in a second rank tensor. 7

• (Eqn. 4 -4) can be expressed matricially as: (4 -5) • Equation 4 -5 can be expressed in indicial notation, where (4 -6) • The symbol is usually omitted, and the Einstein’s summation rule used. (4 -7) Free Subscript “dummy” Subscript (appears twice) 8

Transformations • Transformation of vector p [p 1, p 2, p 3 ] from reference system x 1, x 2, x 3 to reference x’ 1, x’ 2, x’ 3 can be carried p out as follows X’ 3 X’ 2 X 1 X’ 1 where = Angle between X’i. Xj New Old 9

• In vector notation: p = p 1 i 1 + p 2 i 2 + p 3 i 3 where i 1, i 2, and i 3 are unit vectors (4 -8) p’ = p 1 cos(X’ 1 X 1) + p 2 cos(X’ 1 X 1) + p 3 cos(X’ 1 X 1) = a 11 p 1 + a 12 p 2 + a 13 p 3 New (4 -9) Old where aij = cos (X’i. Xj) is the direction cosine between X’i and Xj. 10

• The nine angles that the two systems form are as follows: Old System New System = (4 -10) This is known as the TRANSFORMATION Matrix 11

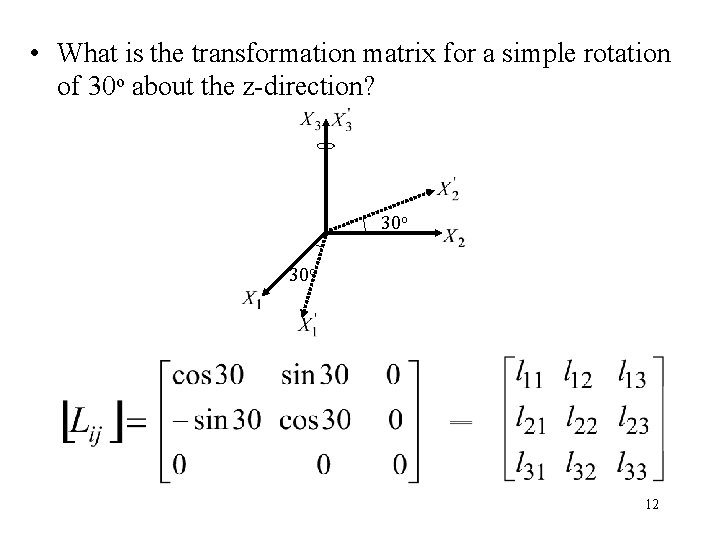
• What is the transformation matrix for a simple rotation of 30 o about the z-direction? 30 o 12

• For any Transformation from p to p’, determine the Transformation Matrix and use as follows: (4 -11) This can be written as: (4 -12) • It is also possible to perform the opposite operation, i. e. , new to old (4 -13) 13

• The Transformation of a second rank Tensor [Tkl] from one reference frame to another is given as: (4 -14 a) OR, for stress (4 -14 b) Eqn. 4 -14(a) is the transformation law for tensors and the letters and subscripts are immaterial. • Transformation from new to old system is given as: (4 -15) 14

NOTES on Transformation • Transformation does not change the physical integrity of the tensor, only the components are transformed. • Stress/strain Transformation results in nine components. • Each component of the transformed 2 nd rank tensor has nine terms. • lij and Tij are completely different, although both have nine components. – Lij is the relationship between two systems of reference. – Tij is a physical entity related to a specific system of reference. 15

Transformation of the stress tensor ij from the system of axes to the • We use eqn. 4 -14: – First sum over j = 1, 2, 3 – Then sum over i = 1, 2, 3 (4 -16) 16

• For each value of k and l there will be an equation similar to eqn. 4 -16. • To find the equation for the normal stress in the x’ 1 direction, let m = 1 and n = 1. • Let us determine the shear stress on the x’ plane and the z’ direction, that is ’ 13 or x’z’ for which m = 1 and n = 3 17

• The General definition of the Transformation of an nth-rank tensor from one reference system to another (i. e. , T T’) is given by: T’mno……. = lmilnjlok……………. Tijk………. . (4 -16) Note that aij = lmi (the letters are immaterial) • The transformation does not change the physical integrity of the tensor, only the components are transformed 18