The various engineering and true stressstrain properties obtainable

• The various engineering and true stress-strain properties obtainable from a tension test are summarized by the categorized listing of Table 1. 1. • Note that the engineering fracture strain f and the % elongation are only different ways of stating the same quantity. Also, the %RA and f can be calculated from each other. • Note that the strength coefficient H determines the magnitude of the true stress in the large strain region of the stress-strain curve, and so it is included as a measure of strength. • The strain hardening exponent n is a measure of the rate of strain hardening.

Table 1. 1 Materials Properties Obtainable from Tension Tests

Modulus of Elasticity • The slope of the initial portion of the stress-strain curve is the modulus of elasticity, or Young’s Modulus. The modulus of elasticity is a measure of the stiffness of the material. It is an important design value. • The modulus of elasticity is determined by the building forces between atoms. It is only slightly affected by alloying.

Measures of Yielding • Yielding defines the point at which plastic deformation begins. This point may be difficult to determine in some materials, which have gradual transition from elastic to plastic behavior. Therefore, various criteria (depends on the sensitivity of the strain measurements) are used to define yielding. 1. Proportional Limit - This is the highest stress at which stress is directly proportional to strain. 2. Elastic Limit - This is the greatest stress the material can withstand without any measurable permanent strain remaining on the complete release of the load. 3. Yield Strength - This is the stress required to produce a small (0. 2% strain) specified amount of plastic deformation.

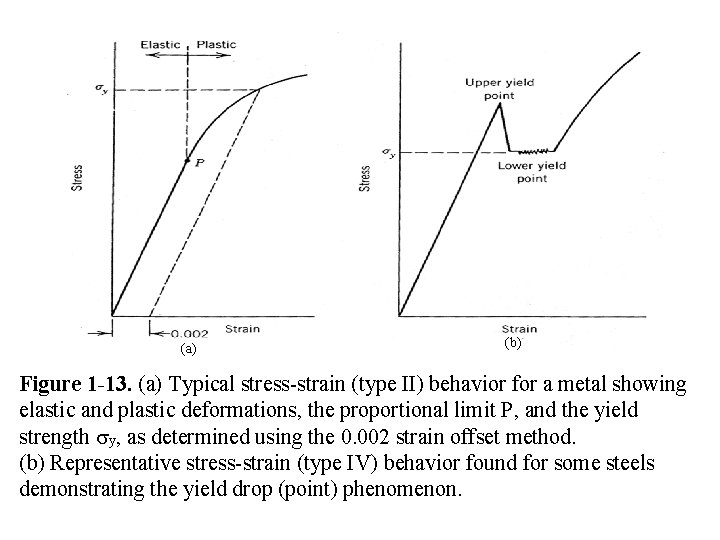
(a) (b) Figure 1 -13. (a) Typical stress-strain (type II) behavior for a metal showing elastic and plastic deformations, the proportional limit P, and the yield strength y, as determined using the 0. 002 strain offset method. (b) Representative stress-strain (type IV) behavior found for some steels demonstrating the yield drop (point) phenomenon.

Poisson’s Ratio • If the applied stress is uniaxial (only in the z direction), then x = y. A parameter termed Poisson’s ratio v is defined as the ratio of the lateral and axial strains, or (1. 8) z x Figure 1 -14. (1. 9) (1. 10)

Measures of Ductility • Ductility is a qualitative, subjective property of a material. It usually indicates the extent to which a metal can be deformed without fracture. • Two methods one can obtain ductility from tension test are: - the engineering strain at fracture, ef, known as elongation where (1. 11) - the reduction in area at fracture, q where (1. 12)

• The two properties are obtained by putting the fractured specimen back together, and taking measurements of Lf and Af. • Both elongation and reduction of area are usually expressed as a percentage. • The value of ef will depend on the gage length Lo in necked specimens. The reduction in area is a better method of reporting elongation, especially for ductile materials.

Toughness • The toughness of a material is its ability to absorb energy in the plastic range. This property is particular desirable in parts such as freight car couplings, gears, chains, and crane hooks. • One way of looking at toughness is to consider it as the total area under the stress- strain curve. This area is an indication of the amount of work per unit volume which can be done on the material without causing it to rupture. • Figure 1 -15 shows the stress strain curve for high and low toughness materials.

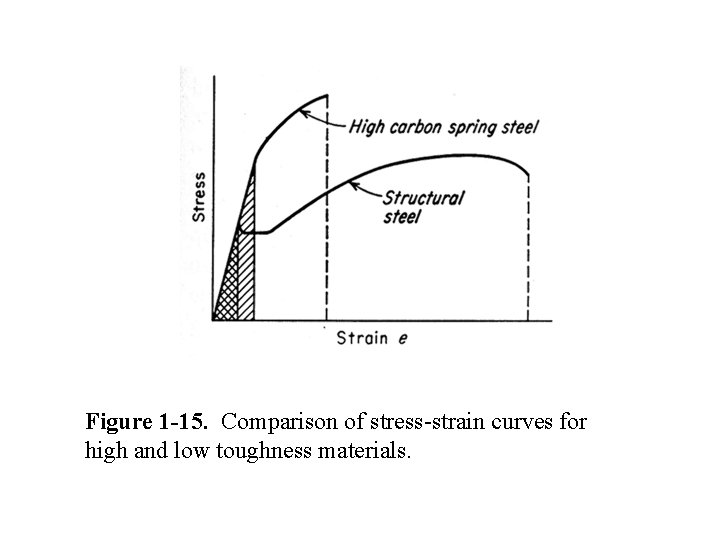
Figure 1 -15. Comparison of stress-strain curves for high and low toughness materials.

• The area under the curve for ductile metals (stress-strain curve is like that of the structural steel) can be approximated by either of the following equations: (1. 13) or (1. 14) • The area under the curve for brittle materials (stress-strain curve is sometimes assumed to be a parabola) can be given by: (1. 15) • All these relations are only approximately to the area under the stress-strain curve.

Resilience • The ability of a material to absorb energy when deformed elastically is called resilience. Otherwise called modulus of resilience, it is the strain energy per unit volume required to stress the material from zero stress to the yield stress o. The strain energy per unit volume for uniaxial tension is (1. 16) • From the above definition the modulus of resilience is (1. 17)

Resilience Continued. . . • The value can be obtained by integrating over the area under the curve up to the yield point, and this is given as: (1. 18 a) • Assuming a linear elastic region, (1. 18 b) (1. 19)

True Stress-True Strain Curve • The relationship between the true stress, , and engineering stress, s, is given by: (1. 20) where P is the Load, and Ao is the original length • The derivation of Eq. (1. 20) assumes both constancy of volume and a homogenous distribution of strain along the gage length of the tension specimen. Thus, Eq. (1. 20) should only be used until the onset of necking.

• It must be emphasized that the engineering stress-strain curve does not give a true indication of the deformation characteristics of a metal because it is based on the original dimensions of the specimen. • In actuality, ductile materials continue to strain-harden up to fracture, but engineering stress-strain curve gives a different picture. The occurrence of necking in ductile materials leads to a drop in load and engineering stress required to continue deformation, once the maximum load is exceeded. • An assessment of the true stress-true strain curve provides a realistic characteristic of the material.

• Beyond maximum load the true stress should be determined from actual measurements of load and cross-sectional area. (1. 21) • The true strain may be determined from the engineering or conventional strain e by (1. 22) • This equation is applicable only to the onset of necking for the reasons discussed above.

• Beyond maximum load the true strain should be based on actual area or diameter measurements. (1. 23) • Figure 1 -16 compares the true-stress true-strain curve for AISI 4140 hot-rolled steel with its corresponding engineering stress-strain curve.

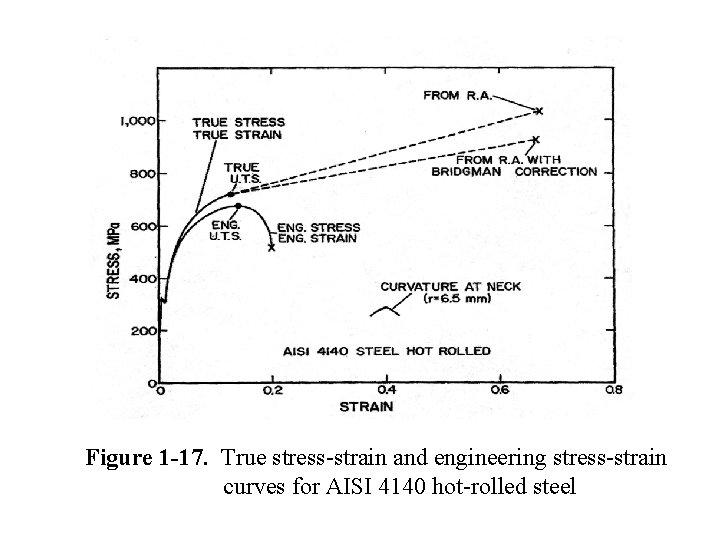
Figure 1 -17. True stress-strain and engineering stress-strain curves for AISI 4140 hot-rolled steel

• The annealed structure is ductile, but has low yield stress. The ultimate tensile stresses (the maximum engineering stresses) are marked by arrows. After these points, plastic deformation becomes localized (called necking), and the engineering stresses drop because of the localized reduction in cross-sectional area. • However, the true stress continues to rise because the cross -sectional area decreases and the material work-hardens in the neck region. The true-stress-true-strain curves are obtained by converting the tensile stress and its corresponding strain into true values and extending the curve.

Instability in Tension Necking or localized deformation begins at maximum load, where the increase in stress due to decrease in the cross-sectional area of the specimen becomes greater than the increase in the load-carrying ability of the metal due to strain hardening. This conditions of instability leading to localized deformation is defined by the condition d. P = 0. (1. 24) From the constancy-of-volume relationship, (1. 25)

From the instability condition, (1. 26 a) so that at a point of tensile instability (1. 26 b) The necking criterion can be expressed more explicitly if engineering strain is used. Starting with Eq. (1. 26 b ) (1. 27)

We know that the volume V is constant in plastic deformation: Consequently, In what follows, we use the subscripts e and for engineering (nominal) and true stresses and strains, respectively. We have

(1. 28) • On the other hand, the incremental longitudinal true strain is defined as (1. 29) • For extended deformation, integration is required: (1. 30)

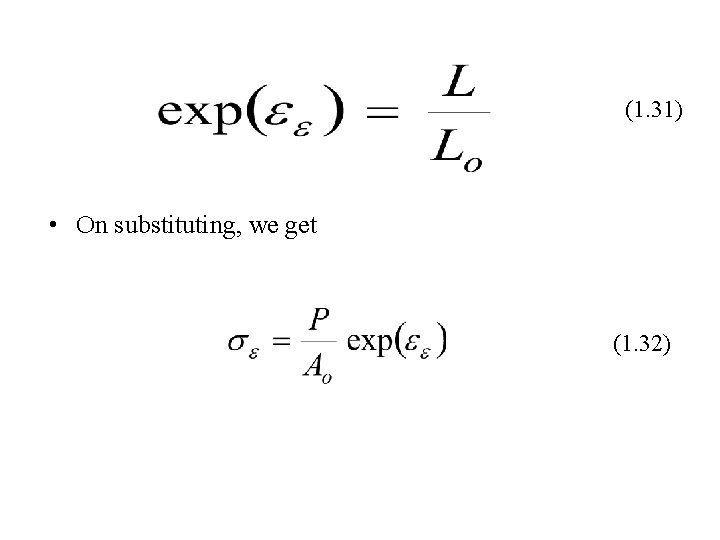
(1. 31) • On substituting, we get (1. 32)

True Stress at Maximum Load and Eliminating Pmax yields and (1. 29)

True Fracture Strain • The true fracture strain, f , is the true strain based of the original area Ao and the area after fracture Af. (1. 30) • For cylindrical tensile specimens the reduction of area q is related to the true fracture strain by the relationship (1. 31)