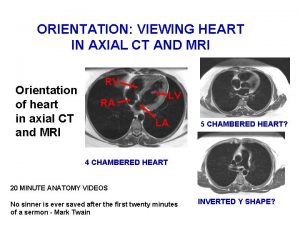
Definition of normal stress axial stress Definition of

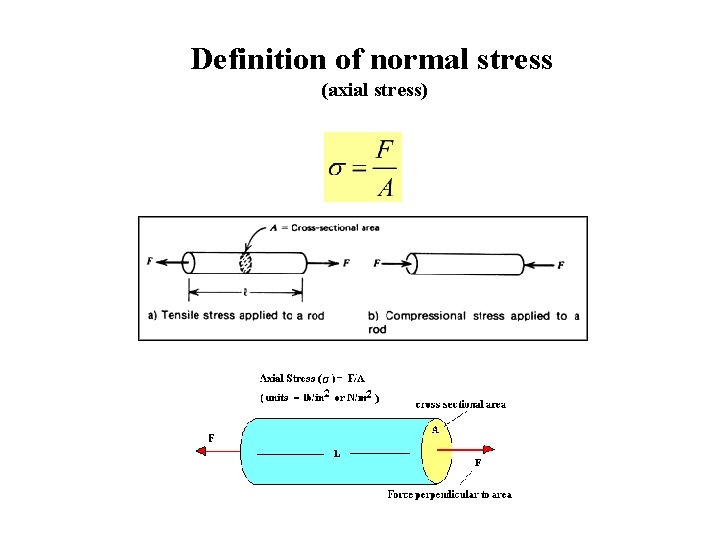
Definition of normal stress (axial stress)

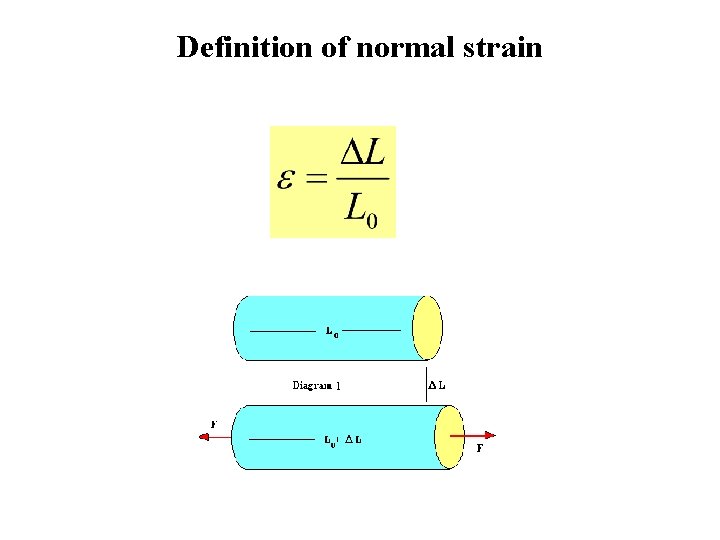
Definition of normal strain

Poisson’s ratio

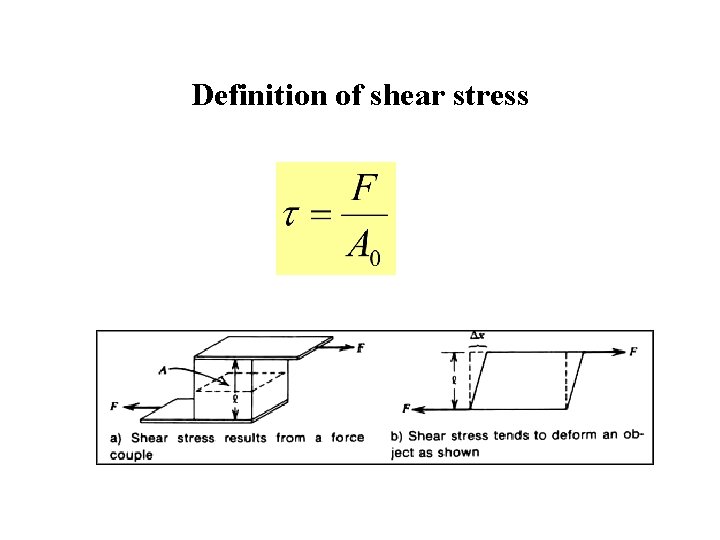
Definition of shear stress

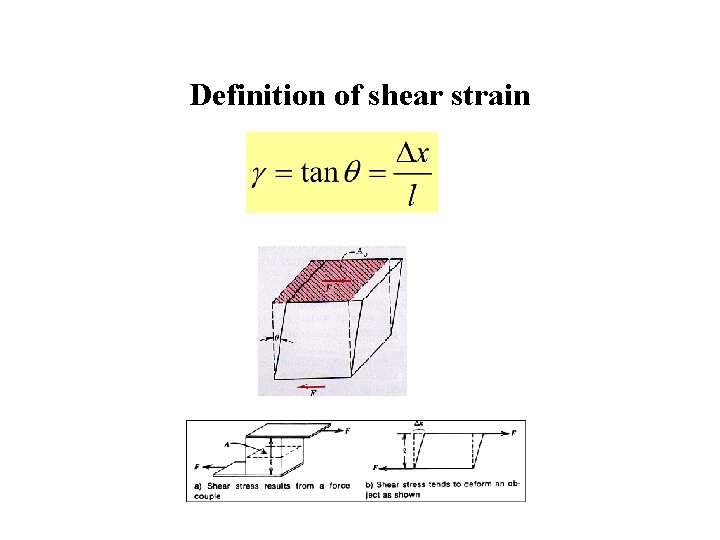
Definition of shear strain

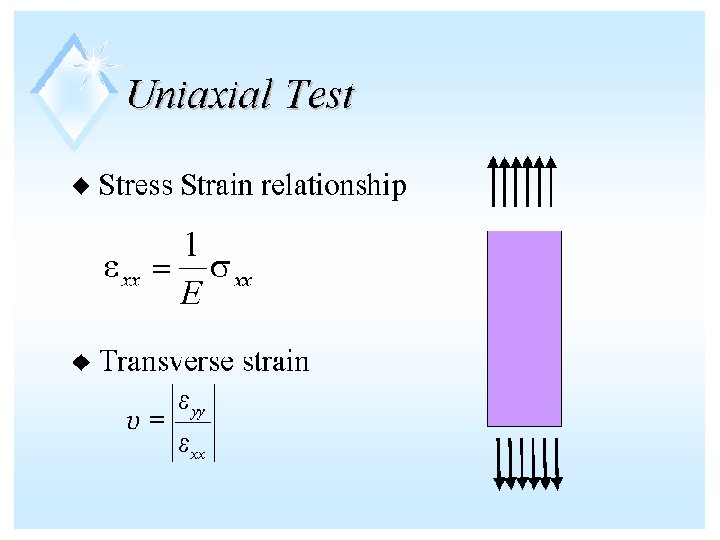
Tensile Testing

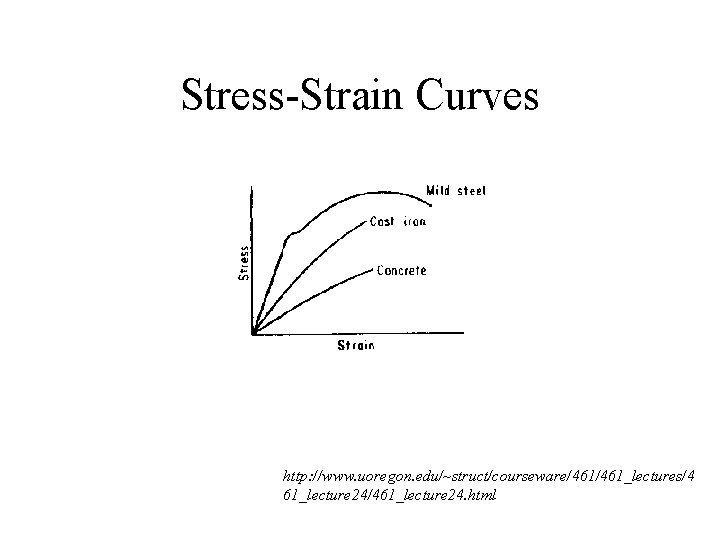
Stress-Strain Curves

Stress-Strain Curves http: //www. uoregon. edu/~struct/courseware/461_lectures/4 61_lecture 24/461_lecture 24. html

Stress-Strain Curve (ductile material) http: //www. shodor. org/~jingersoll/weave/tutorial/node 4. html

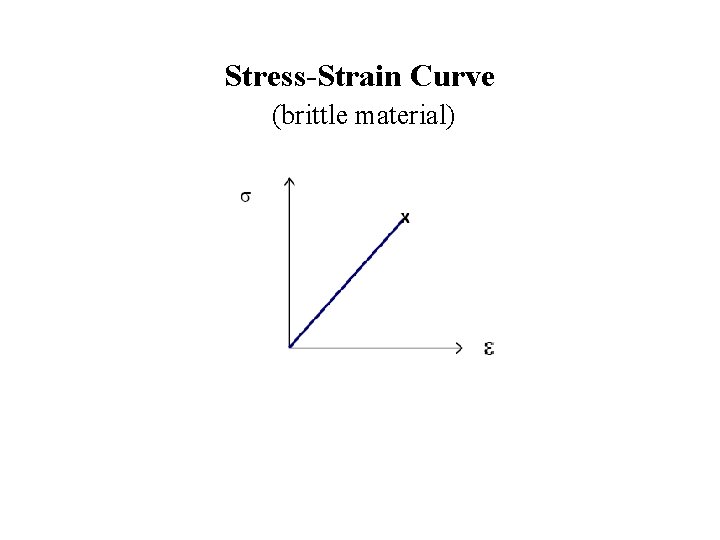
Stress-Strain Curve (brittle material)

Example: stress-strain curve for low-carbon steel • 1 - Ultimate Strength • 2 - Yield Strength • 3 - Rupture • 4 - Strain hardening region • 5 - Necking region Hooke's law is only valid for the portion of the curve between the origin and the yield point. http: //en. wikipedia. org/wiki/Hooke's_law

σPL ⇒ Proportional Limit - Stress above which stress is not longer proportional to strain. σEL ⇒ Elastic Limit - The maximum stress that can be applied without resulting in permanent deformation when unloaded. σYP ⇒ Yield Point - Stress at which there are large increases in strain with little or no increase in stress. Among common structural materials, only steel exhibits this type of response. σYS ⇒ Yield Strength - The maximum stress that can be applied without exceeding a specified value of permanent strain (typically. 2% =. 002 in/in). OPTI 222 Mechanical Design in Optical Engineering 21 σU ⇒ Ultimate Strength - The maximum stress the material can withstand (based on the original area)

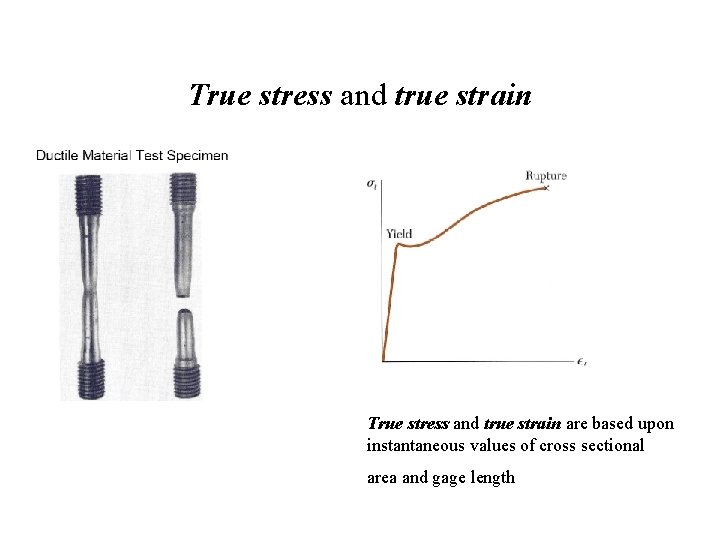
True stress and true strain are based upon instantaneous values of cross sectional area and gage length

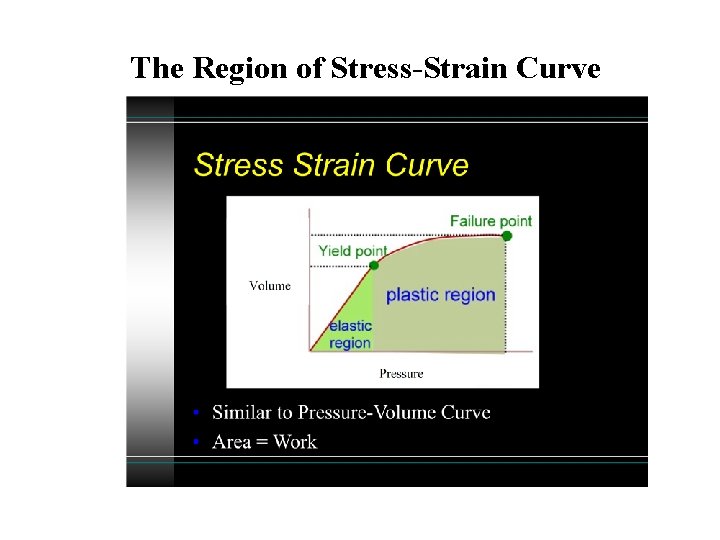
The Region of Stress-Strain Curve

Uni-axial Stress State Elastic analysis

Stress-Strain Relationship Hooke’s Law: E -- Young’s modulus G -- shear modulus

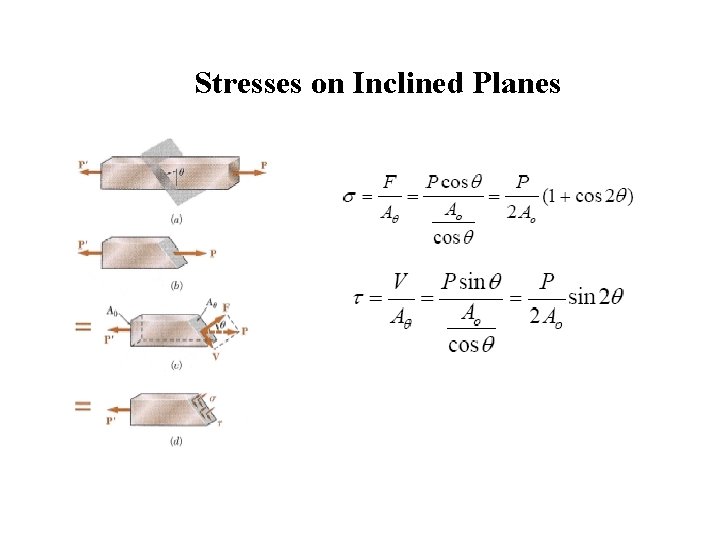
Stresses on Inclined Planes

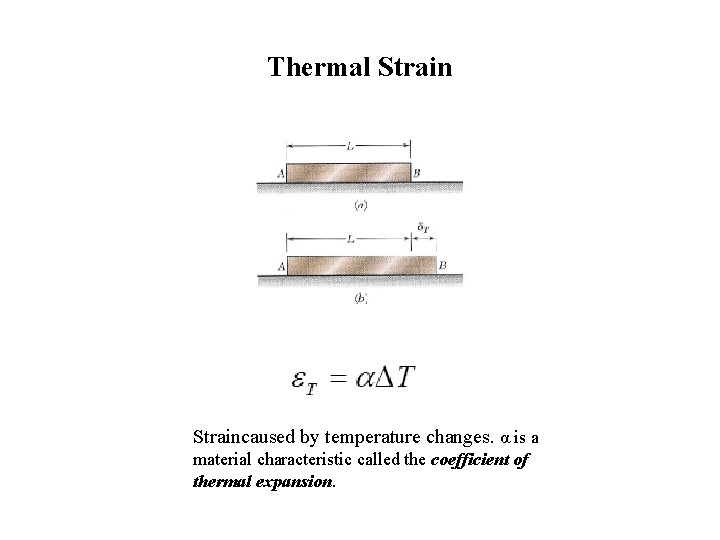
Thermal Straincaused by temperature changes. α is a material characteristic called the coefficient of thermal expansion.

Strains caused by temperature changes and strains caused by applied loads are essentially independent. Therefore, the total amount of strain may be expressed as follows:

Bi-axial state elastic analysis

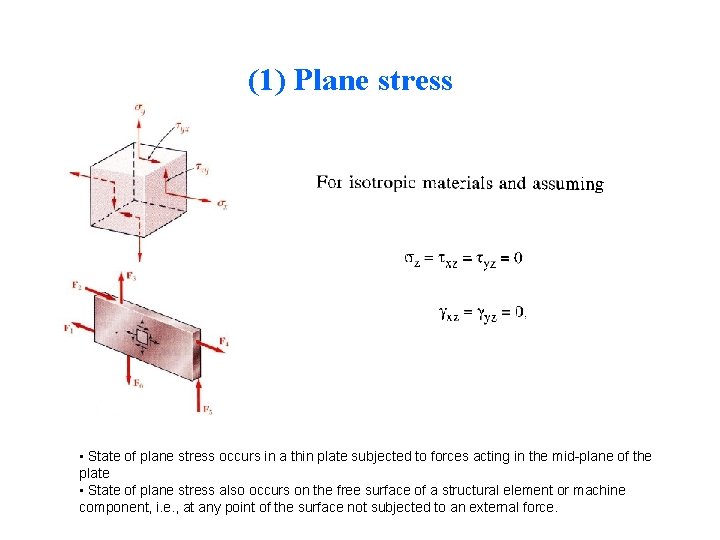
(1) Plane stress • State of plane stress occurs in a thin plate subjected to forces acting in the mid-plane of the plate • State of plane stress also occurs on the free surface of a structural element or machine component, i. e. , at any point of the surface not subjected to an external force.

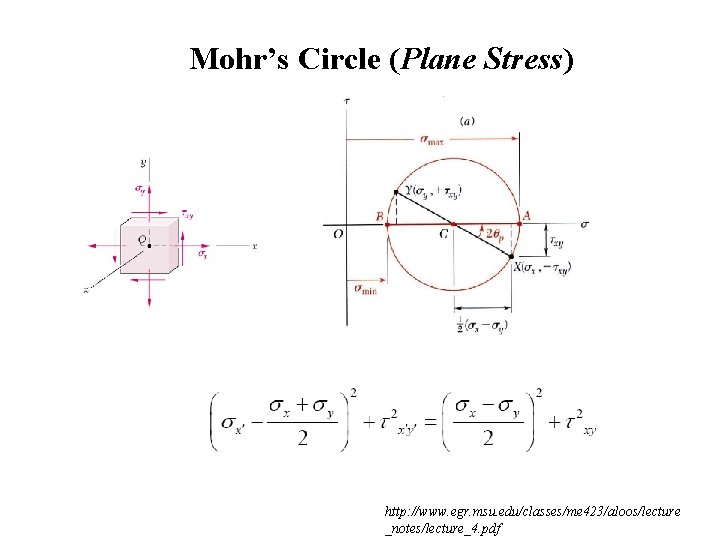
Transformation of Plane Stress

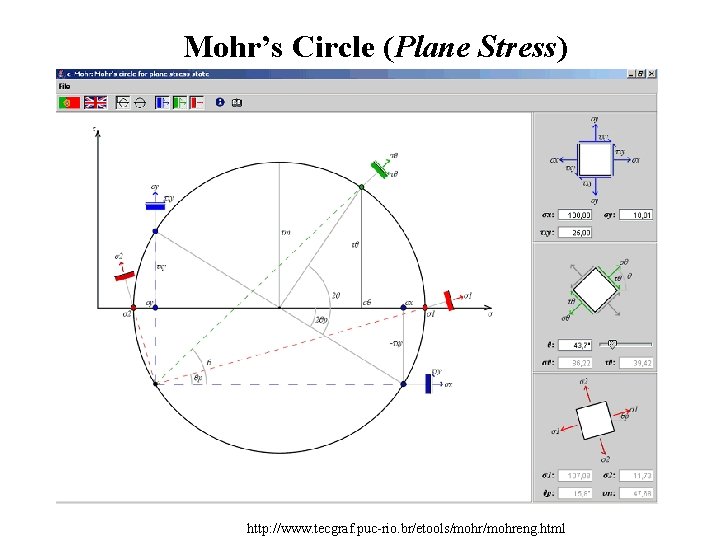
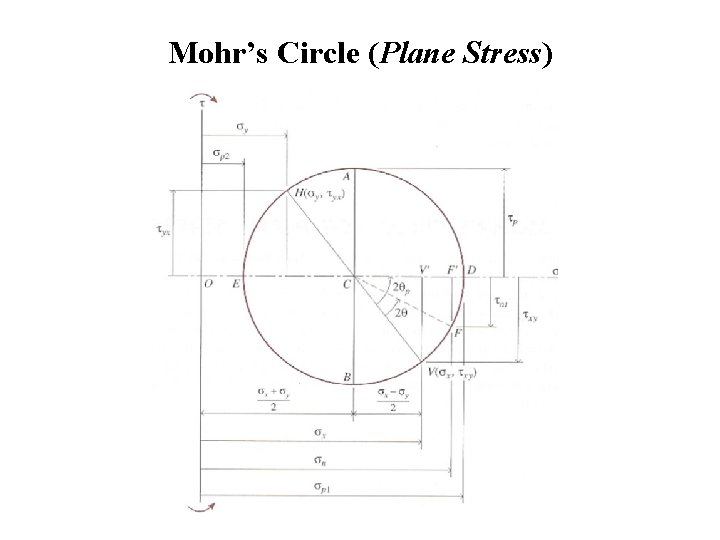
Mohr’s Circle (Plane Stress) http: //www. tecgraf. puc-rio. br/etools/mohreng. html

Mohr’s Circle (Plane Stress)

Instruction to draw Mohr’s Circle 1. Determine the point on the body in which the principal stresses are to be determined. 2. Treating the load cases independently and calculated the stresses for the point chosen. 3. Choose a set of x-y reference axes and draw a square element centered on the axes. 4. Identify the stresses σx, σy, and τxy = τyx and list them with the proper sign. 5. Draw a set of σ - τ coordinate axes with σ being positive to the right and τ being positive in the upward direction. Choose an appropriate scale for the each axis. 6. Using the rules on the previous page, plot the stresses on the x face of the element in this coordinate system (point V). Repeat the process for the y face (point H). 7. Draw a line between the two point V and H. The point where this line crosses the σ axis establishes the center of the circle. 8. Draw the complete circle. 9. The line from the center of the circle to point V identifies the x axis or reference axis for angle measurements (i. e. θ = 0). Note: The angle between the reference axis and the σ axis is equal to 2θp.

Mohr’s Circle (Plane Stress) http: //www. egr. msu. edu/classes/me 423/aloos/lecture _notes/lecture_4. pdf

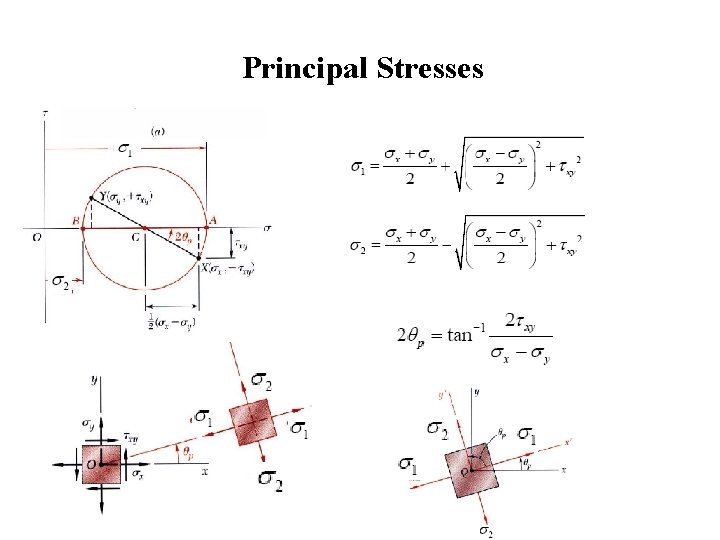
Principal Stresses

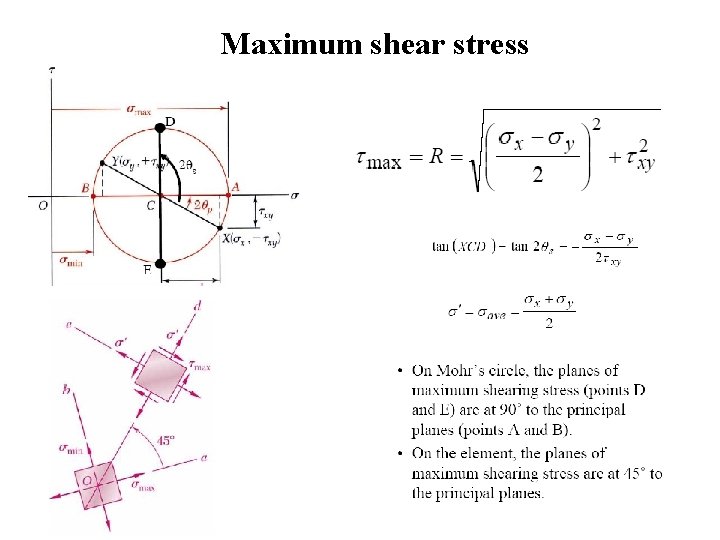
Maximum shear stress

Stress-Strain Relationship (Plane stress) http: //www 4. eas. asu. edu/concrete/elasticity 2_95/sld 001. htm

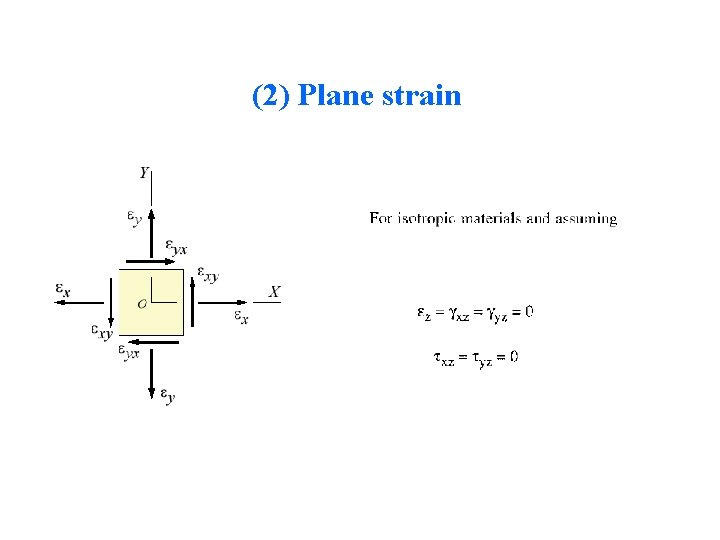
(2) Plane strain

Coordinate Transformation The transformation of strains with respect to the {x, y, z} coordinates to the strains with respect to {x', y', z'} is performed via the equations

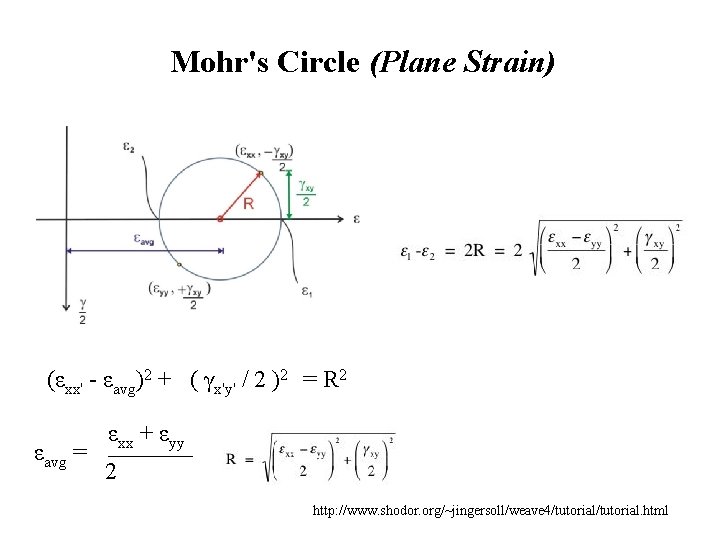
Mohr's Circle (Plane Strain) (εxx' - εavg)2 + ( γx'y' / 2 )2 = R 2 εavg = εxx + εyy 2 http: //www. shodor. org/~jingersoll/weave 4/tutorial. html

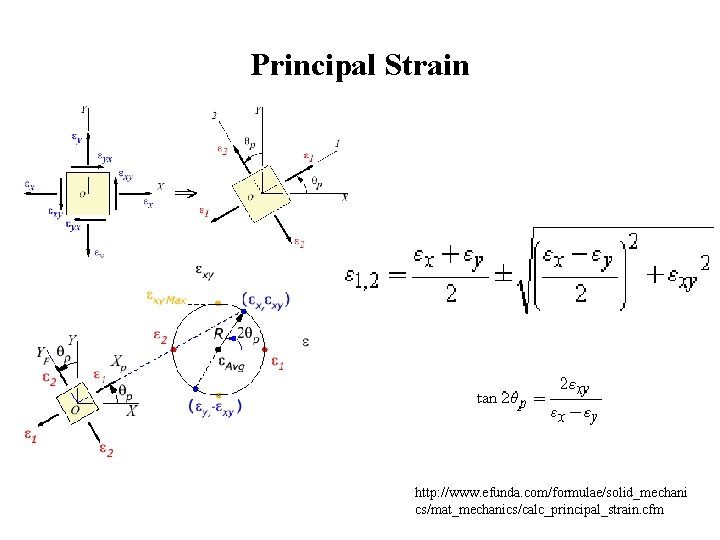
Principal Strain http: //www. efunda. com/formulae/solid_mechani cs/mat_mechanics/calc_principal_strain. cfm

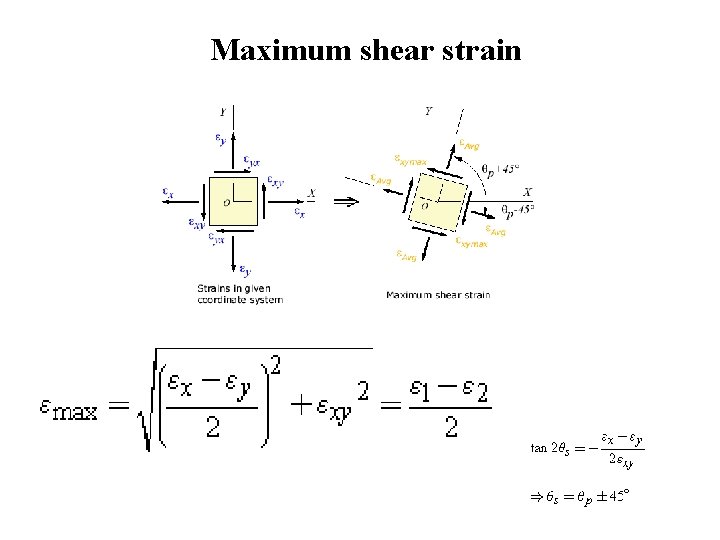
Maximum shear strain

Stress-Strain Relationship (Plane strain)

Tri-axial stress state elastic analysis

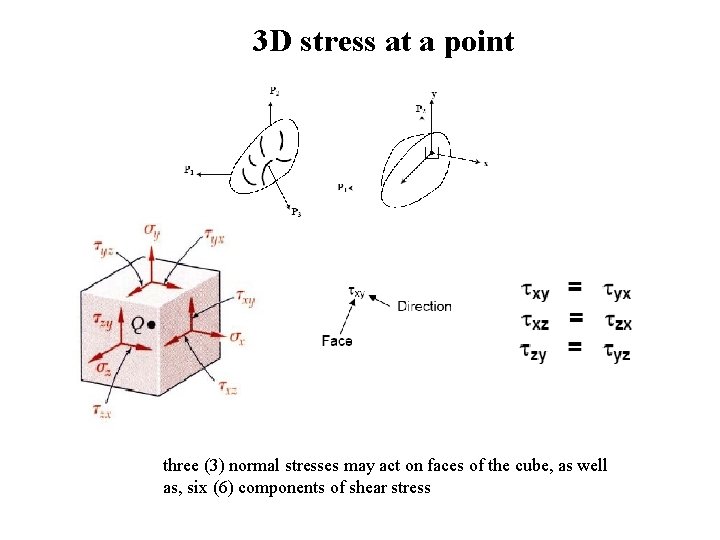
3 D stress at a point three (3) normal stresses may act on faces of the cube, as well as, six (6) components of shear stress

Stress and strain components

The stress on a inclined plane (l, m, n) z p y x

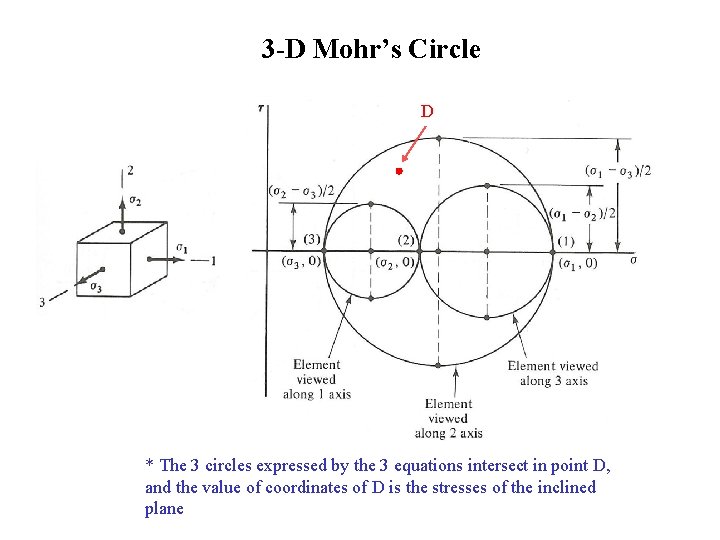
3 -D Mohr’s Circle D * The 3 circles expressed by the 3 equations intersect in point D, and the value of coordinates of D is the stresses of the inclined plane

Stress-Strain Relationship Generalized Hooke’s Law: For isotropic materials