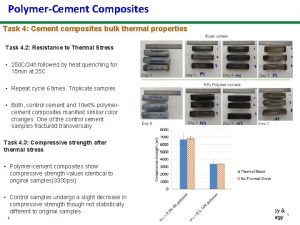
27 301 MicrostructureProperties Composites part 4 Absorbing Shocks

27 -301 Microstructure-Properties Composites: part 4 Absorbing Shocks Profs. A. D. Rollett, M. De Graef Processing Performance Microstructure Properties Last modified: 18 th Dec. ‘ 15

2 Lecture Objectives: Composites • The main objective of this lecture is to introduce you to microstructure-property relationships in composite materials. • We discuss the way in which cellular materials are useful for absorbing shocks and how to quantify this property. • This is an example of the application of composite properties of foams, which are cellular materials. Please acknowledge Carnegie Mellon if you make public use of these slides

3 Q&A for Part 4 1. What are the main differences in the response of metal foams, ceramic foams and polymer foams to compression (crushing)? One obvious difference is that metals and ceramics typically crush in an irreversible fashion whereas most polymer foams recover (visco-)elastically. 2. (#6) How is it that foams can absorb large amounts of energy? The most important feature of their stress-strain curves is the large strain at constant stress (the plateau region), which means that there is a large area under the curve. 3. (#8) How do we translate a stress-strain curve into maps of Energy Absorbed versus Peak Stress? Integrate the curve to get the area and adjust the units to get energy; plot this value versus the max. stress. Why is it that the Energy does not increase much beyond a certain point? Because the foam starts to approach full density, which means that the stress rises sharply with little increase in strain. 4. How is it possible for foams (esp. polymers) to deform at constant stress over large strains? Through bending and deformation of the cell walls. 6. In the plots of energy absorbed versus normalized stress, how do we obtain the envelopes at constant density? By identifying the point on the energystress curves where the stress enters the plateau region (#10). 7. For a shock cushion, how do we calculate the energy absorbed and the maximum stress? By computing (W*A*t), #14. 8. How does the drop height specify the energy that must be absorbed? Via the kinetic energy, #11. What about the strain rate? From velocity / thickness, #12. 9. In the worked example, how do we get the quantities such as energy absorbed and normalized stress in order to use the graphs provided for specific materials? From the kinetic energy (above) and the mass, specified max. deceleration and area, #11. 10. In the worked example for expanded polyurethane, how does the iterative procedure work to arrive at a suitable thickness for the shock cushion that satisfies the requirement for maximum stress and for the strain rate? By varying the thickness of the foam pad and re-computing the energies, strain rates etc. until convergence is obtained. Please acknowledge Carnegie Mellon if you make public use of these slides

4 Advertising Looks pretty good, right? How does it work? How can we check it out? With all the reporting on concussion of athletes, shock protection is obviously important. Please acknowledge Carnegie Mellon if you make public use of these slides

Examinable 5 Cellular Materials • This next section provides some basic information on cellular materials. • Why study cellular materials? Answer: cellular materials provide a range of properties that are not achievable in bulk materials. Especially when load carrying capacity at very low densities is required, only cellular materials can satisfy the requirements. Shock resistance is also a vital characteristic of cellular materials. • Cellular structures are feasible (and used for engineering applications) with all materials types. Metal honeycombs are used in transport applications. Ceramic foams are used in insulation. Cellular structures are ubiquitous in biomaterials (wood, bone, shells…). • A good basic reference is Cellular Solids, Pergamon, L. J. Gibson and M. F. Ashby (1988), ISBN 0 -08 -036607 -4. Please acknowledge Carnegie Mellon if you make public use of these slides

6 Examinable Honeycombs: properties • Note the contrast between tension and compression (plateau present), 4. 2 a vs. 4. 2 b. • Even brittle wall materials exhibit progressive failure in compression, 4. 2 e. • The stress-strain curves are labeled by their characteristic stages. • Very important consequences for energy absorbing structures (see later slides) [Gibson & Ashby: Cellular Materials] Please acknowledge Carnegie Mellon if you make public use of these slides

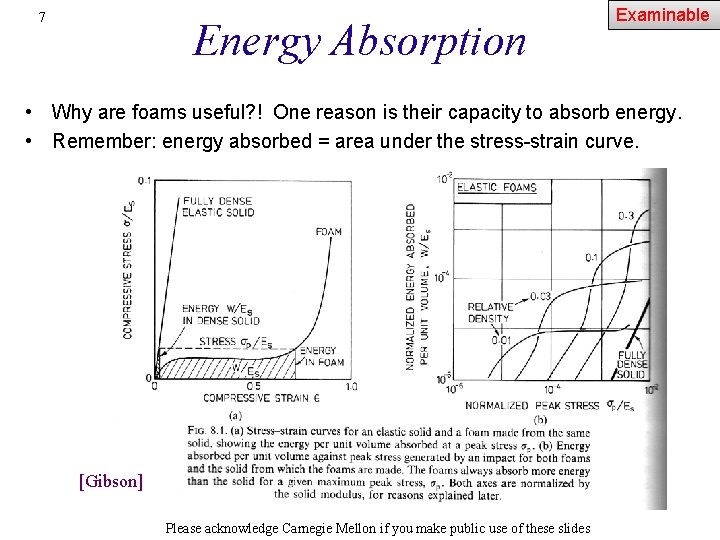
7 Energy Absorption Examinable • Why are foams useful? ! One reason is their capacity to absorb energy. • Remember: energy absorbed = area under the stress-strain curve. [Gibson] Please acknowledge Carnegie Mellon if you make public use of these slides

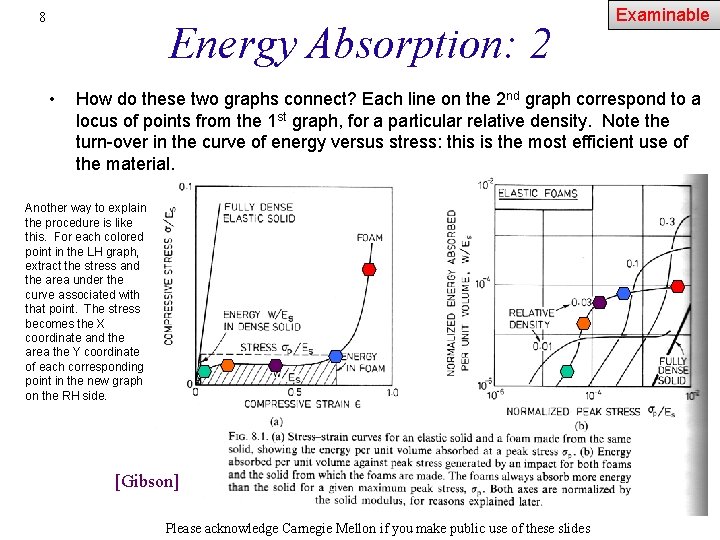
8 Energy Absorption: 2 • Examinable How do these two graphs connect? Each line on the 2 nd graph correspond to a locus of points from the 1 st graph, for a particular relative density. Note the turn-over in the curve of energy versus stress: this is the most efficient use of the material. Another way to explain the procedure is like this. For each colored point in the LH graph, extract the stress and the area under the curve associated with that point. The stress becomes the X coordinate and the area the Y coordinate of each corresponding point in the new graph on the RH side. [Gibson] Please acknowledge Carnegie Mellon if you make public use of these slides

9 Energy Absorption: 3 Examinable During wall buckling, densification proceeds at a approximately constant external stress. Fully Densified [Gibson] Wall Buckling Elastic Note that, once the foam starts to densify (steep upturn in the stress-strain curve) then the stress rises with little increase in energy absorbed. Please acknowledge Carnegie Mellon if you make public use of these slides

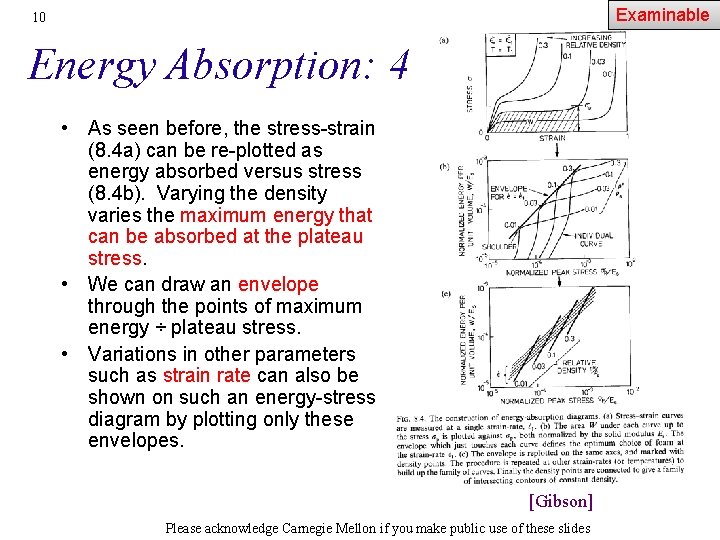
Examinable 10 Energy Absorption: 4 • As seen before, the stress-strain (8. 4 a) can be re-plotted as energy absorbed versus stress (8. 4 b). Varying the density varies the maximum energy that can be absorbed at the plateau stress. • We can draw an envelope through the points of maximum energy ÷ plateau stress. • Variations in other parameters such as strain rate can also be shown on such an energy-stress diagram by plotting only these envelopes. [Gibson] Please acknowledge Carnegie Mellon if you make public use of these slides

Examinable 11 Shock Cushions • Once one knows the energy-stress characteristic of a material, it is possible to calculate the optimum thickness. • Given the kinetic energy to be absorbed, U, and the area of contact between object and foam, A, the thickness, t, is given by t=U/WA (Eq. 1) where W is the energy absorbed per unit volume in the foam. • Typically, the mass of the object, m, and the peak deceleration, a, is also specified (as a multiple of gravitational acceleration, g) which determines the maximum stress, s, s = m a / A (Eq. 2) Please acknowledge Carnegie Mellon if you make public use of these slides

Examinable 12 Shock Cushion: 2 • In addition, a drop height is specified which in turn sets the velocity, v, and the energy, U, that must be absorbed; U = m v 2 / 2. Thus the thickness, t, is given by t = m v 2 / (2 W A) (Eq. 3) • This in turn specifies the strain rate, de/dt, in the foam which affects the energy-stress relationship (see Fig. 8. 4 c): de/dt = v / t (Eq. 4) • A good place to start is to identify the maximum allowable stress and read off the associated energy at a high strain rate. The energy is, however, a function of both stress and strain rate, so some iteration is required to identify a suitable thickness that allows the required energy to be absorbed. Please acknowledge Carnegie Mellon if you make public use of these slides

Examinable 13 Shock Cushion: 3 Worked Example Problem specification Mass of packaged object: 500 gms. Area of contact between object and foam: A = 0. 01 m 2 Velocity of package on impact, v = 4. 5 m/s (drop height, h = 1 m) Energy to be absorbed, U = mv 2/2 = 5 J Max. allowable force on package (10 g deceleration), F = ma = 50 N Max. allowable peak stress (Eq. 2), sp = F/A = 5 k. Pa Solid modulus of polyeurethane foam, Es = 50 MPa Max. allowable peak stress, normalized = sp/Es = 0. 0001 We use Gibson-Ashby, fig. 8. 8 (next slide). Gibson & Ashby: Table 8. 2, p. 231 Please acknowledge Carnegie Mellon if you make public use of these slides

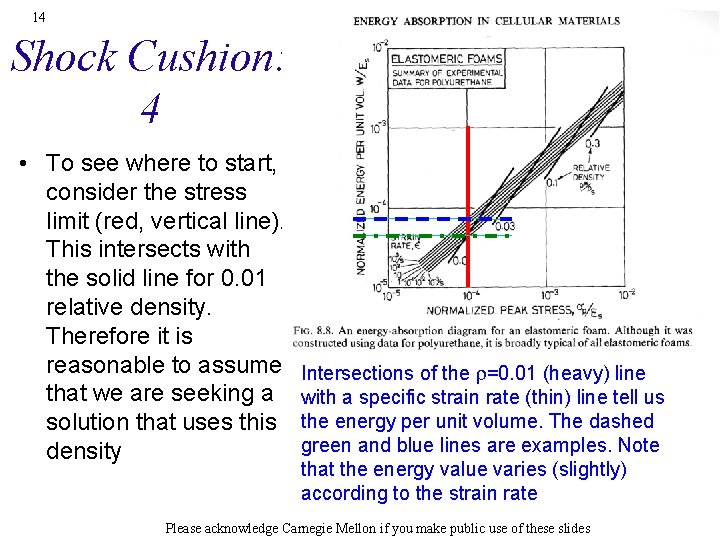
14 Shock Cushion: 4 • To see where to start, consider the stress limit (red, vertical line). This intersects with the solid line for 0. 01 relative density. Therefore it is reasonable to assume Intersections of the r=0. 01 (heavy) line that we are seeking a with a specific strain rate (thin) line tell us solution that uses this the energy per unit volume. The dashed green and blue lines are examples. Note density that the energy value varies (slightly) according to the strain rate Please acknowledge Carnegie Mellon if you make public use of these slides

Examinable [Gibson] 15 Shock Cushion: 5 The reason that we have to iterate is that changing the thickness changes the strain rate and therefore the W value. To start working on the problem, we have to make some rather arbitrary choices of thickness that bracket the likely result. Choice of thickness, t: 1 m Strain rate, de/dt=v/t (Eq 4): 4. 5 s-1 Energy/modulus (W/Es) at sp/Es = 0. 0001: (Fig. 8. 8) 5. 25 10 -5 Energy absorbed/unit volume: 2. 62 k. J/m 3 Energy absorbed (W*A*t): 26. 2 J 0. 001 m 4500 s-1 7. 4 10 -5 3. 70 k. J/m 3 0. 037 J To complete the problem, we have to iterate on the thickness until we converge on a self-consistent result and the energy absorbed is the required value, 5 J. Please acknowledge Carnegie Mellon if you make public use of these slides

[Gibson] 16 Examinable Shock Cushion: 6 To continue with the problem, we re-calculate thicknesses from Eq. 1. Thickness, t = U/WA: 0. 19 m 0. 14 m Strain rate, de/dt=v/t (Eq 4): 24 s-1 32 s-1 Energy/modulus (W/Es) at sp/Es = 0. 0001: (Fig. 8. 8) 6. 6 10 -5 6. 7 10 -5 Energy absorbed/unit volume: 3. 30 k. J/m 3 3. 35 k. J/m 3 Energy absorbed: 6. 27 J 4. 69 J Clearly we have nearly converged, so we have to iterate on the thickness one more time, using t = U/WA, which gives t= 150 mm, W*A*t=5 J, and an optimum relative density = 0. 01. Please acknowledge Carnegie Mellon if you make public use of these slides

Examinable 17 Summary: Part 4 • Foams or cellular materials are an example of composite materials. • We developed an example of how cellular materials are useful as shock cushions. • This lead to worked example of how calculate the optimum thickness of such as shock cushion. Please acknowledge Carnegie Mellon if you make public use of these slides

18 Questions • Many of us commonly use Wikipedia to learn about new topics or to check information. What do you think of this wiki page? http: //en. wikipedia. org/wiki/Shock_absorber Please acknowledge Carnegie Mellon if you make public use of these slides

19 References • • • Cellular Solids, Pergamon, L. J. Gibson and M. F. Ashby (1988), ISBN 0 -08036607 -4. L. Gong, S. Kyriakides, W. -Y. Jang, “Compressive response of open-cell foams; Part I: Morphology and elastic properties”, Intl. J. Solids Structures, 42 (2005) 1355 -1379. Materials Principles & Practice, Butterworth Heinemann, edited by C. Newey & G. Weaver. Mechanical Behavior of Materials, T. H. Courtney (2000), Boston, Mc. Graw-Hill. Mechanical Behavior of Materials, N. E. Dowling (1999), Prentice-Hall. Structural Materials, Butterworth Heinemann, edited by G. Weidmann, P. Lewis and N. Reid. The New Science of Strong Materials, J. E. Gordon, Princeton. An Introduction of Composite Products, Chapman & Hall, K. Potter (1997), ISBN 0412 -73690 -X. An Introduction to the Mechanical Properties of Solid Polymers, Wiley, I. M. Ward and D. W. Hadley (1993), ISBN 0 -471 -93887 -4. Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials, Cambridge University Press, 2009, S. Nemat-Nasser, ISBN 0521108063. Theory of Composites, Cambridge University Press, 2001, G. F. Milton, ISBN 0521781256. Please acknowledge Carnegie Mellon if you make public use of these slides

20 Supplemental Slides • The following slides contain supplemental material that will be of interest to those who are curious to obtain more detail. Please acknowledge Carnegie Mellon if you make public use of these slides