Yet another decision procedure for Equality Logic Ofer

(Yet another) decision procedure for Equality Logic Ofer Strichman and Orly Meir Technion 1

Equality Logic n E: 0 0 0 1 (x 1 = x 2 Æ (x 2 = x 3 Ç x 1 x 3)) n Domain: x 1, x 2, x 3 2 N n The satisfiability problem: is there an assignment to x 1, x 2, x 3 that satisfies E ? n Q: When is Equality Logic useful ? . . . Technion 2

Equality Logic 0 0 0 1 n E: (x 1 = x 2 Æ (x 2 = x 3 Ç x 1 x 3)) n A: Mainly when combined with Uninterpreted Functions f(x, y), g(z), … n Mainly used in proving equivalences, but not only. Technion 3

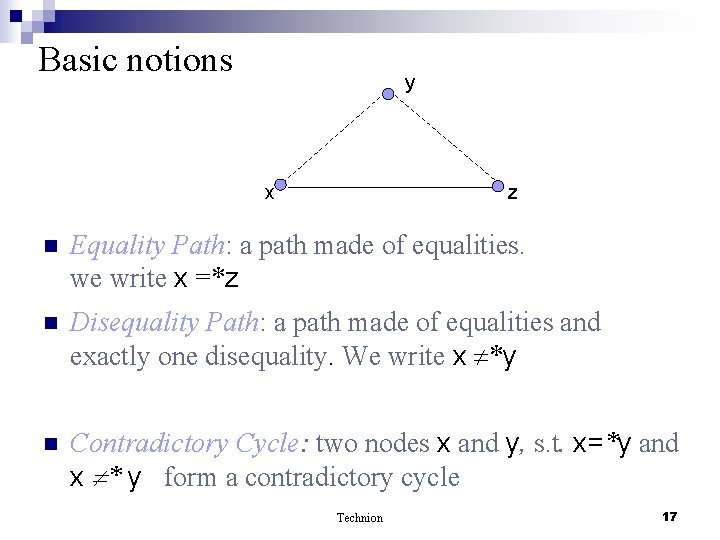
Basic notions E: x = y Æ y = z Æ z x (non-polar) Equality Graph: y x z Gives an abstract view of E Technion 4

From Equality to Propositional Logic E : x 1 = x 2 Æ x 2 = x 3 Æ x 1 x 3 B: e 1, 2 Æ e 2, 3 Æ : e 1, 3 x 1 e 1 , 2 e 1, 3 Bryant & Velev CAV’ 00 – the Sparse method x 2 e 2, 3 x 3 n Encode all edges with Boolean variables ¨ This is an abstraction ¨ Transitivity of equality is lost! ¨ Must add transitivity constraints! Technion 5

From Equality to Propositional Logic E : x 1 = x 2 Æ x 2 = x 3 Æ x 1 x 3 B: e 1, 2 Æ e 2, 3 Æ : e 1, 3 x 1 e 1 , 2 e 1, 3 Bryant & Velev CAV’ 00 – the Sparse method x 2 e 2, 3 x 3 n Transitivity Constraints: For each cycle of size n, forbid a true assignment to n-1 edges T S = (e 1, 2 Æ e 2, 3 ! e 1, 3) Æ (e 1, 2 Æ e 1, 3 ! e 2, 3) Æ (e 1, 3 Æ e 2, 3 ! e 1, 2) Check: B Æ T S Technion 6

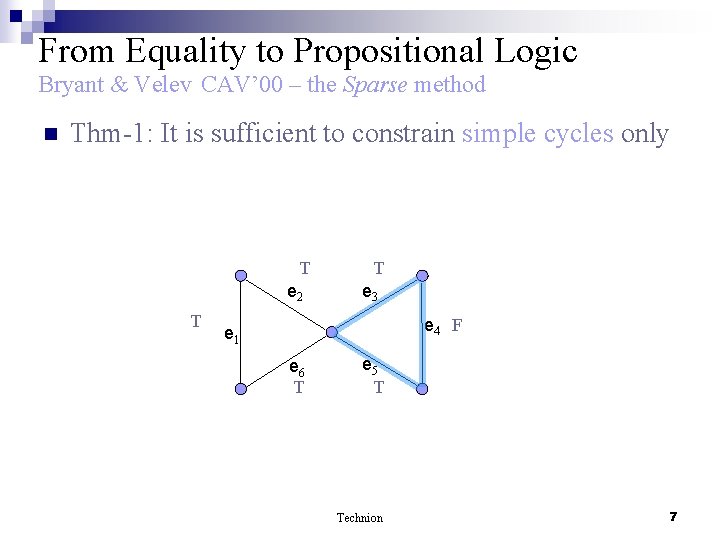
From Equality to Propositional Logic Bryant & Velev CAV’ 00 – the Sparse method n Thm-1: It is sufficient to constrain simple cycles only T e 2 T T e 3 e 4 F e 1 e 6 T e 5 T Technion 7

From Equality to Propositional Logic Bryant & Velev CAV’ 00 – the Sparse method n Thm-2: It is sufficient to constrain chord-free simple cycles T e 2 T e 5 F e 1 T F e 3 T e 4 Technion 8

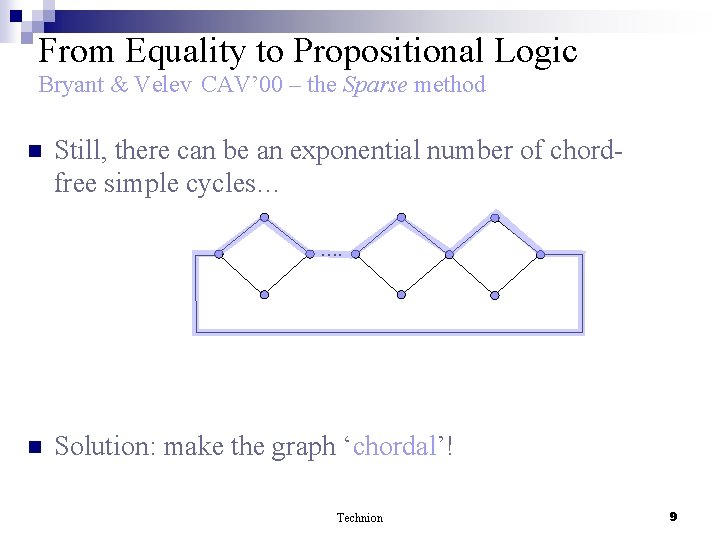
From Equality to Propositional Logic Bryant & Velev CAV’ 00 – the Sparse method n Still, there can be an exponential number of chordfree simple cycles… …. n Solution: make the graph ‘chordal’! Technion 9

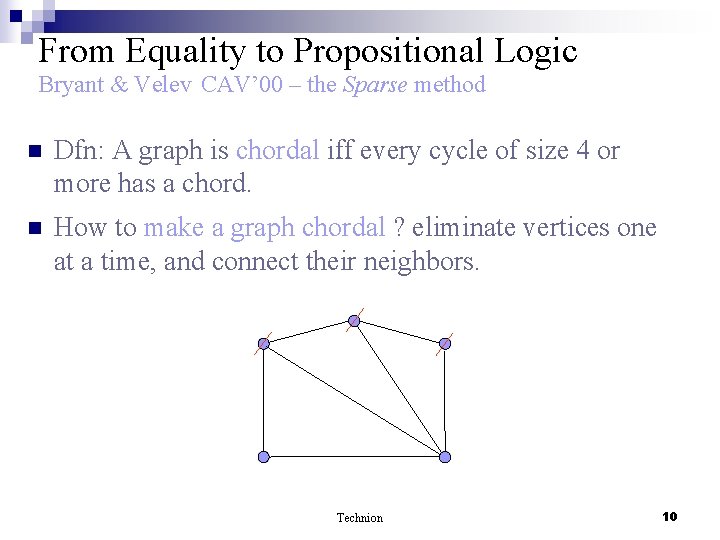
From Equality to Propositional Logic Bryant & Velev CAV’ 00 – the Sparse method n Dfn: A graph is chordal iff every cycle of size 4 or more has a chord. n How to make a graph chordal ? eliminate vertices one at a time, and connect their neighbors. Technion 10

From Equality to Propositional Logic Bryant & Velev CAV’ 00 – the Sparse method n In a chordal graph, it is sufficient to constrain only triangles. T T Contradiction! T T F T T n Polynomial # of edges and constraints. n # constraints = 3 £ #triangles Technion 11

An improvement Reduced Transitivity Constraints (RTC) n So far we did not consider the polarity of the edges. E: x = y Æ y = z Æ z x n Assuming E is in Negation Normal Form y (polar) Equality Graph: x = = Technion z 12

Monotonicity of NNF n Thm-3: NNF formulas are monotonically satisfied (in CNF this is simply the pure literal rule) n Let be in NNF and satisfiable. Thm-3 implies: ¨ Let ² ’ from by switching the value of a ‘mis-assigned’ pure literal in ¨ Derive ¨ Now ’ ² Technion 13

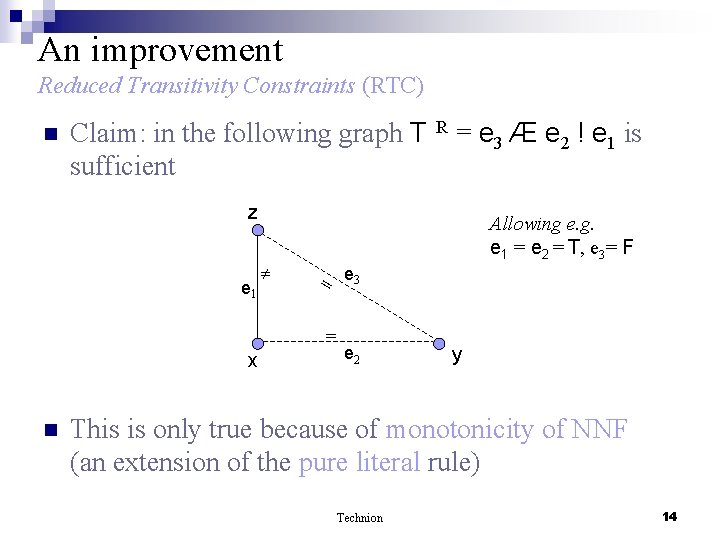
An improvement Reduced Transitivity Constraints (RTC) n Claim: in the following graph T sufficient R = e 3 Æ e 2 ! e 1 is z e 1 Allowing e. g. e 1 = e 2 = T, e 3= F = e 3 = x n e 2 y This is only true because of monotonicity of NNF (an extension of the pure literal rule) Technion 14

Basic notions y x z n Equality Path: a path made of equalities. we write x =*z n Disequality Path: a path made of equalities and exactly one disequality. We write x *y n Contradictory Cycle: two nodes x and y, s. t. x=*y and x * y form a contradictory cycle Technion 17

Basic notions n Thm-4: Every contradictory cycle is either simple or contains a simple contradictory cycle Technion 18

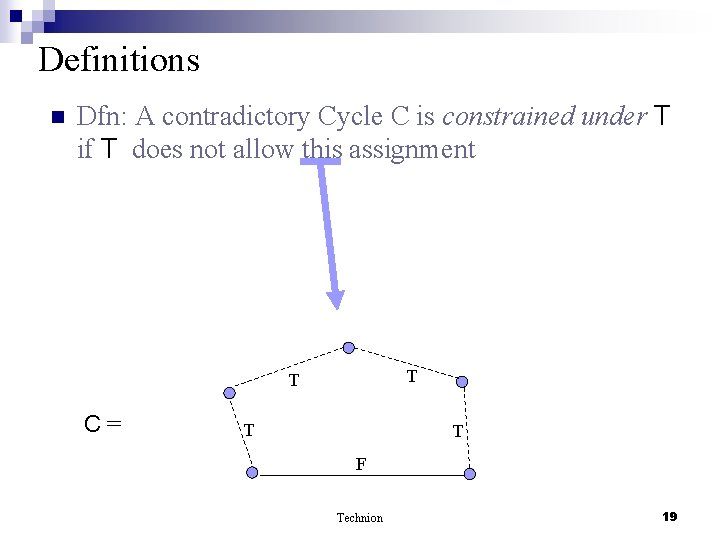
Definitions n Dfn: A contradictory Cycle C is constrained under T if T does not allow this assignment T T C= T T F Technion 19

Main theorem n If T R constrains all simple contradictory cycles, and S S For every assignment , ² T n S! S ²TR From the Sparse method then E is satisfiable iff B Æ T R is satisfiable The Equality Formula Technion 21

Proof of the main theorem n ( ) E is satisfiable BÆT S is satisfiable BÆT R is satisfiable n ( ) Proof strategy: R be a satisfying assignment to B Æ T R ¨ We will construct S that satisfies B Æ T S ¨ From this we will conclude that E is satisfiable ¨ Let Skip proof Technion 22

Definitions for the proof… n A Violating cycle under an assignment R: F e. T 1 T Either dashed or solid T e. T 2 n This assignment violates T S but not necessarily T R Technion 23

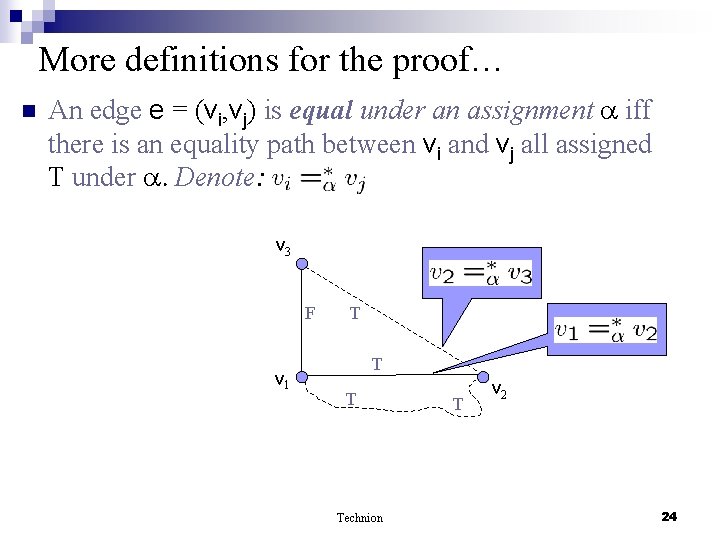
More definitions for the proof… n An edge e = (vi, vj) is equal under an assignment iff there is an equality path between vi and vj all assigned T under . Denote: v 3 F v 1 T Technion T v 2 24

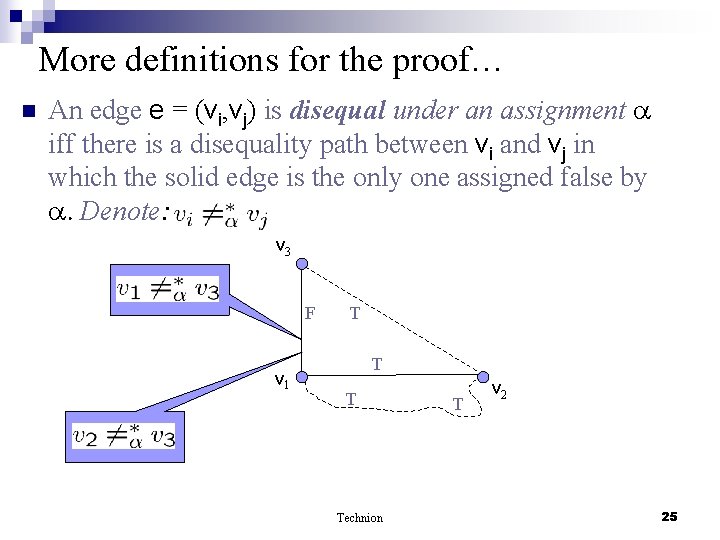
More definitions for the proof… n An edge e = (vi, vj) is disequal under an assignment iff there is a disequality path between vi and vj in which the solid edge is the only one assigned false by . Denote: v 3 F v 1 T Technion T v 2 25

Proof… n Observation 1: The combination is impossible if = R (recall: R ² T R) v 3 F T v 1 n T v 2 Observation 2: if (v 1, v 3) is solid, then Technion 26

Re. Constructing S Type 1: Type 2: It is not the case that Otherwise it is not the case that v 3 F F T T v 1 n T v 1 v 2 Assign S (e 23) = F n v 2 Assign (e 13) = T In all other cases S = R Technion 27

Re. Constructing S n Starting from R, repeat until convergence: (e. T) : = F in all Type 1 cycles ¨ (e. F) : = T in all Type 2 cycles ¨ n All Type 1 and Type 2 triangles now satisfy T S n B is still satisfied (monotonicity of NNF) n Left to prove: all contradictory cycles are still satisfied Technion 28

Proof… n Invariant: contradictory cycles are not violating throughout the reconstruction. T v 3 F T T v 1 n v 2 contradicts the precondition to make this assignment… Technion 29

Proof… n Invariant: contradictory cycles are not violating throughout the reconstruction. v 3 F T T F v 1 n v 2 contradicts the precondition to make this assignment… Technion 30

Applying RTC n How can we use theorem without enumerating contradictory cycles ? n Answer: ¨ Consider the chordal graph. ¨ Constrain triangles if they are part of a (simple) contradictory cycle ¨ How? Technion 31

n Focus on Bi-connected dashed components built on top of a solid edge ¨ Includes all contradictory cycles involving this edge Technion 33

n Make the component chordal ¨ Chordal-ity guarantees: every cycle contains a simplicial vertex, i. e. a vertex that its neighbors are connected. Technion 34

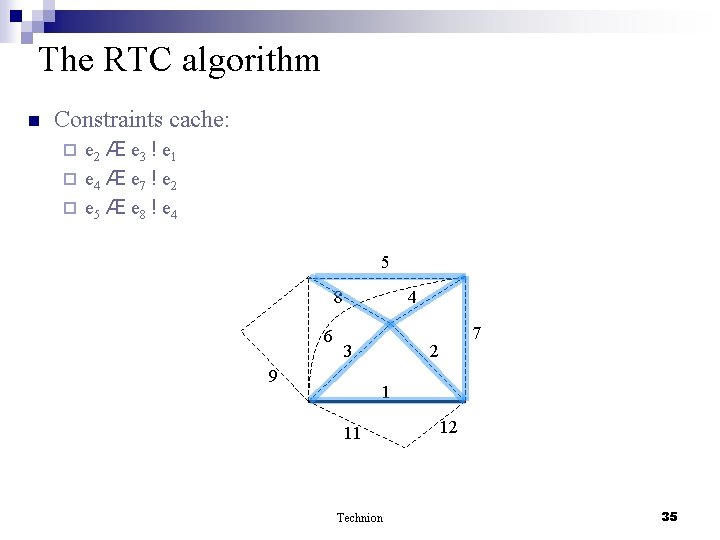
The RTC algorithm n Constraints cache: e 2 Æ e 3 ! e 1 ¨ e 4 Æ e 7 ! e 2 ¨ e 5 Æ e 8 ! e 4 ¨ 5 8 6 4 3 9 7 2 1 11 Technion 12 35

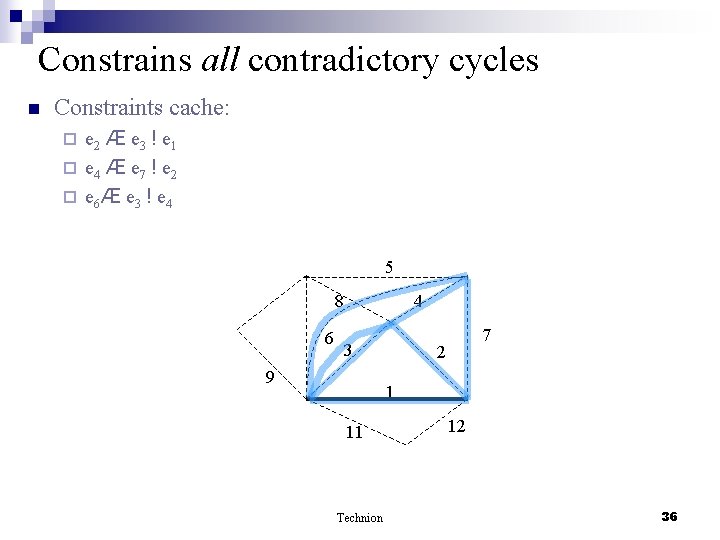
Constrains all contradictory cycles n Constraints cache: e 2 Æ e 3 ! e 1 ¨ e 4 Æ e 7 ! e 2 ¨ e 6 Æ e 3 ! e 4 ¨ 5 8 6 4 3 9 7 2 1 11 Technion 12 36

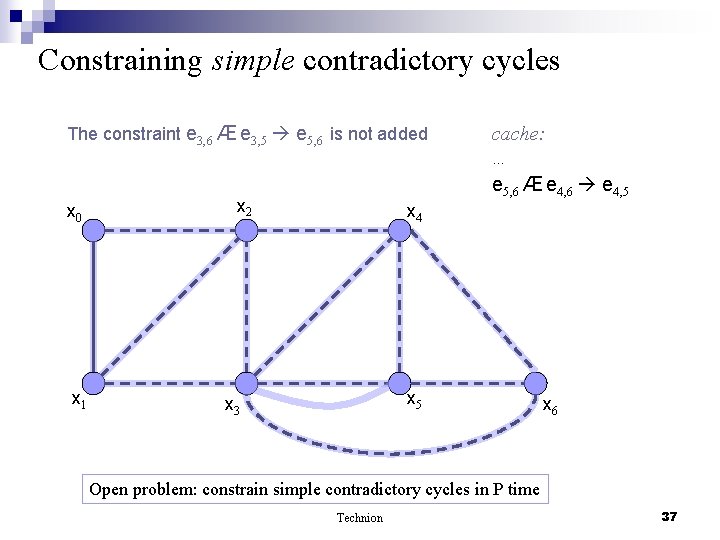
Constraining simple contradictory cycles The constraint e 3, 6 Æ e 3, 5 e 5, 6 is not added x 0 x 1 x 2 cache: … e 5, 6 Æ e 4, 6 e 4, 5 x 4 x 5 x 3 x 6 Open problem: constrain simple contradictory cycles in P time Technion 37

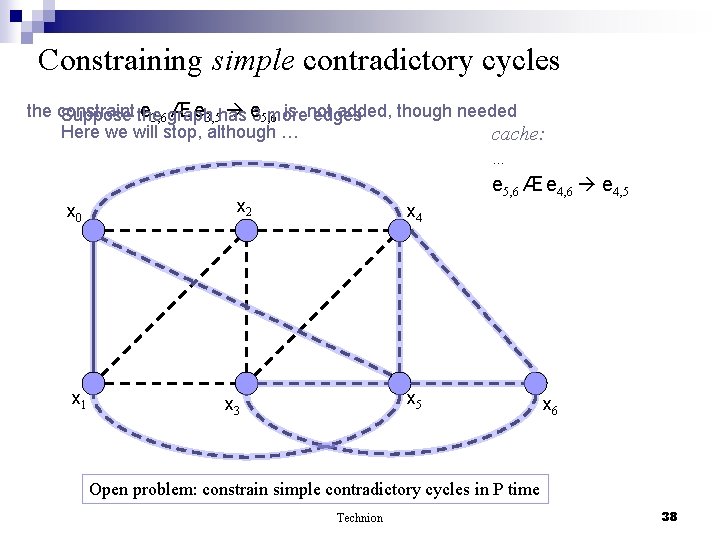
Constraining simple contradictory cycles the constraint e 3, 6 graph Æ e 3, 5 has e 35, 6 is not added, though needed Suppose the more edges Here we will stop, although … cache: x 0 x 1 … e 5, 6 Æ e 4, 6 e 4, 5 x 2 x 4 x 5 x 3 x 6 Open problem: constrain simple contradictory cycles in P time Technion 38

Results Technion 39

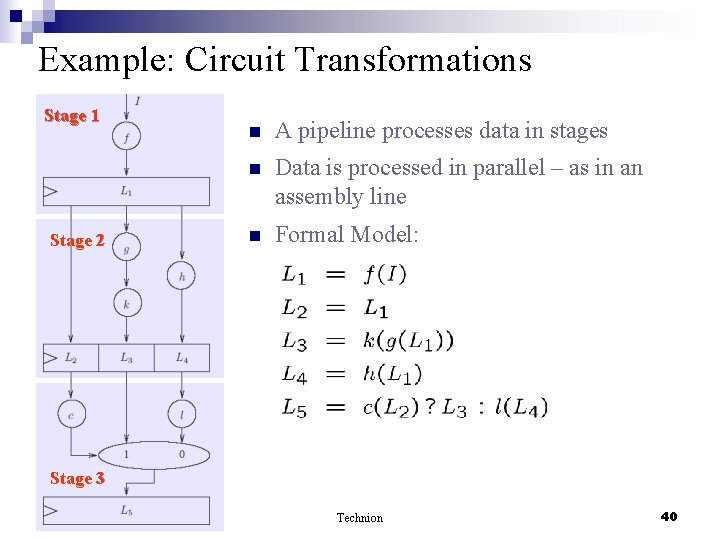
Example: Circuit Transformations Stage 1 Stage 2 n A pipeline processes data in stages n Data is processed in parallel – as in an assembly line n Formal Model: Stage 3 Technion 40

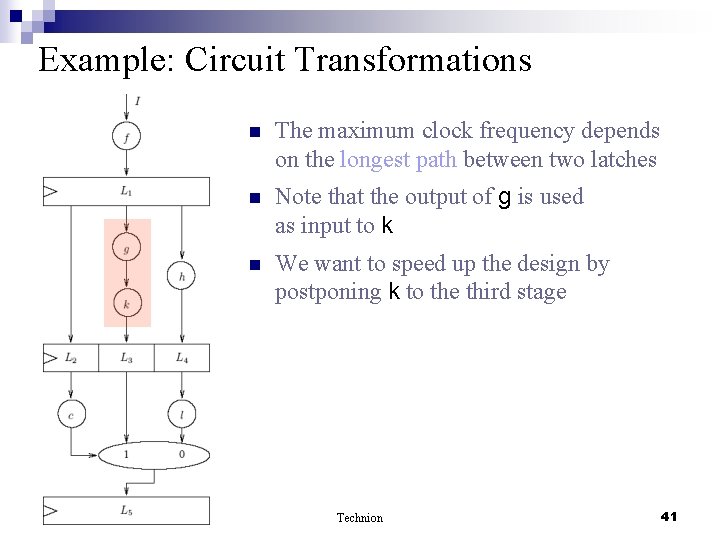
Example: Circuit Transformations n The maximum clock frequency depends on the longest path between two latches n Note that the output of g is used as input to k n We want to speed up the design by postponing k to the third stage Technion 41

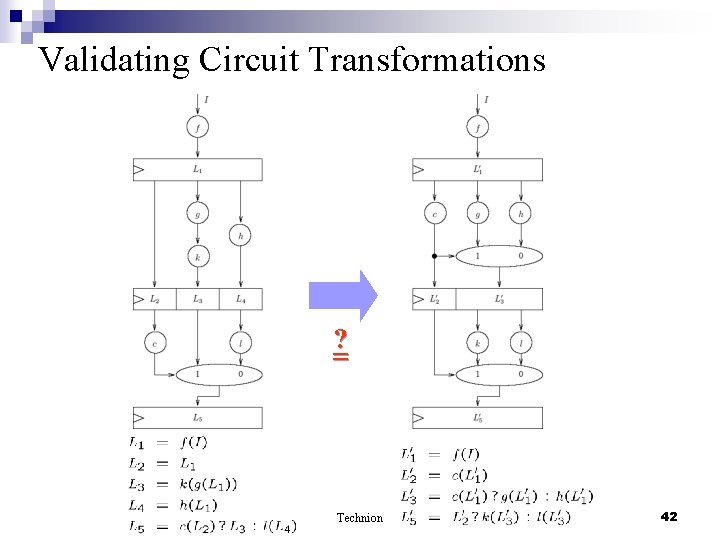
Validating Circuit Transformations ? = Technion 42

Validating a compilation process n Target program n u 1 = x 1 + y 1; u 2 = x 2 + y 2; z = u 1 u 2 ; n Compilation Source program z = (x 1 + y 1) (x 2 + y 2); Need to prove that: (u 1 = x 1 + y 1 u 2 = x 2 + y 2 z = u 1 u 2) $ z = (x 1 + y 1) (x 2 + y 2) Source Target Technion 43

Validating a compilation process n Target program n u 1 = x 1 + y 1; u 2 = x 2 + y 2; z = u 1 u 2 ; n Compilation Source program z = (x 1 + y 1) (x 2 + y 2); Need to prove that: (u 1 = x 1 + y 1 u 2 = x 2 + y 2 z = u 1 u 2) $ z = (x 1 + y 1) (x 2 + y 2) f 1 f 2 g 2 Technion 44

Validating a compilation process n Instead, prove: under functional consistency: for every uninterpreted function f n x = y ! f(x) = f(y) Need to prove that: (u 1 = x 1 + y 1 u 2 = x 2 + y 2 z = u 1 u 2) $ z = (x 1 + y 1) (x 2 + y 2) n Which translates to (via Ackermann’s reduction): g f 1 f 2 g 2 Technion 45