Writing Structured Programs Ernastuti Four iteration statements 1


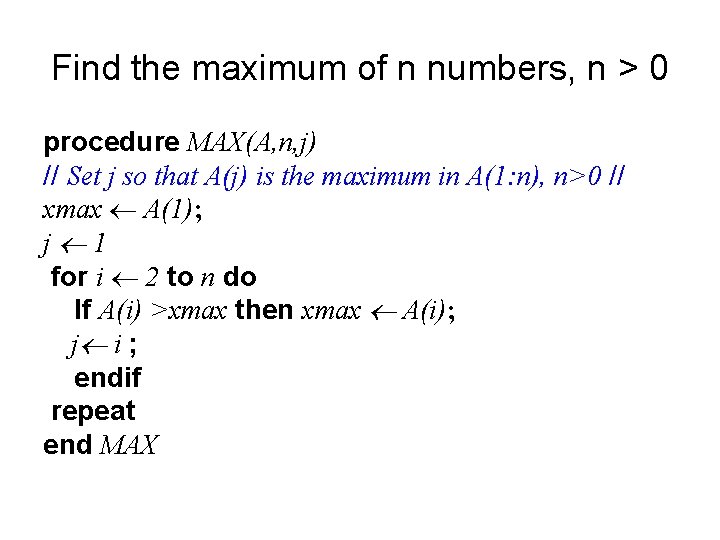



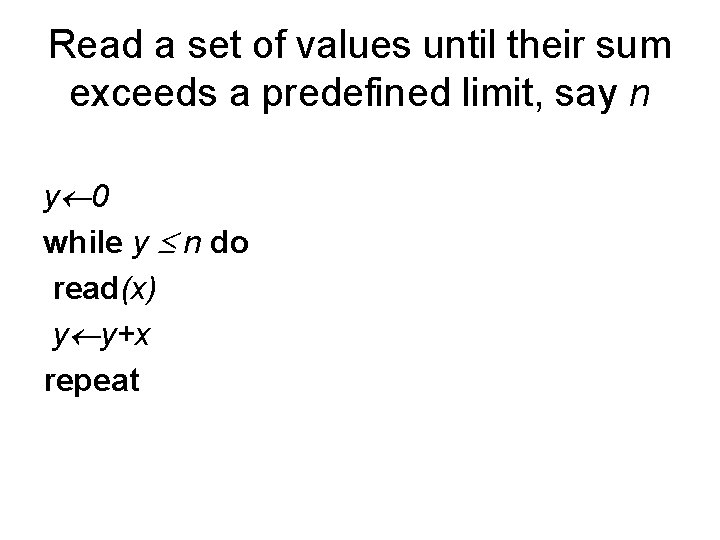











![Insertion Sort Insertion-Sort(A) 1 for j 2 to length[A] 2 do key A[j] 3 Insertion Sort Insertion-Sort(A) 1 for j 2 to length[A] 2 do key A[j] 3](https://slidetodoc.com/presentation_image_h2/6264d249879031cc3fe04b1dad00c18d/image-26.jpg)

- Slides: 27

Writing Structured Programs Ernastuti

Four iteration statements 1. 2. 3. 4. loop-repeat while-repeat loop-until-repeat for-repeat

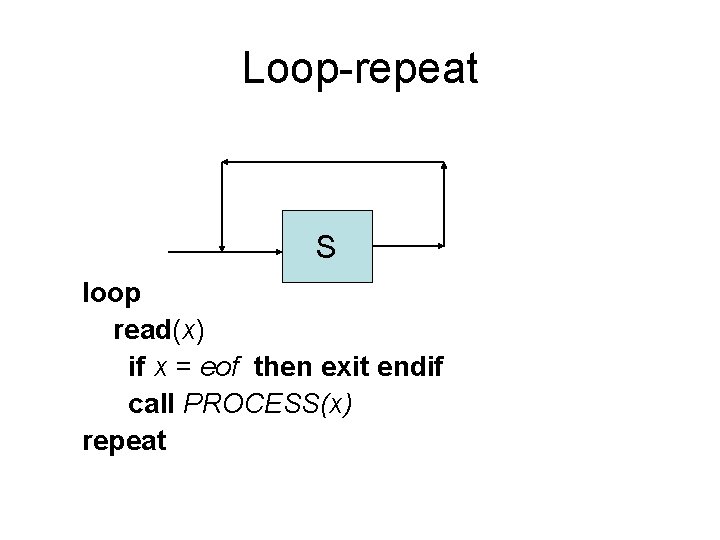
Loop-repeat S loop read(x) if x = eof then exit endif call PROCESS(x) repeat

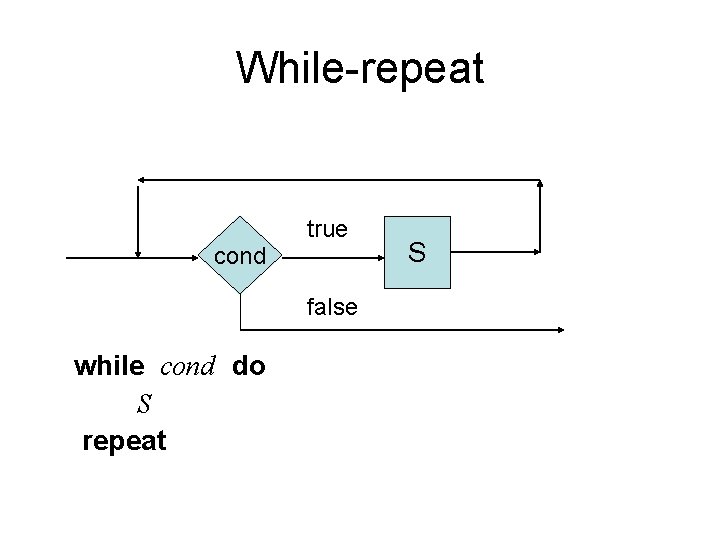
While-repeat true cond false while cond do S repeat S

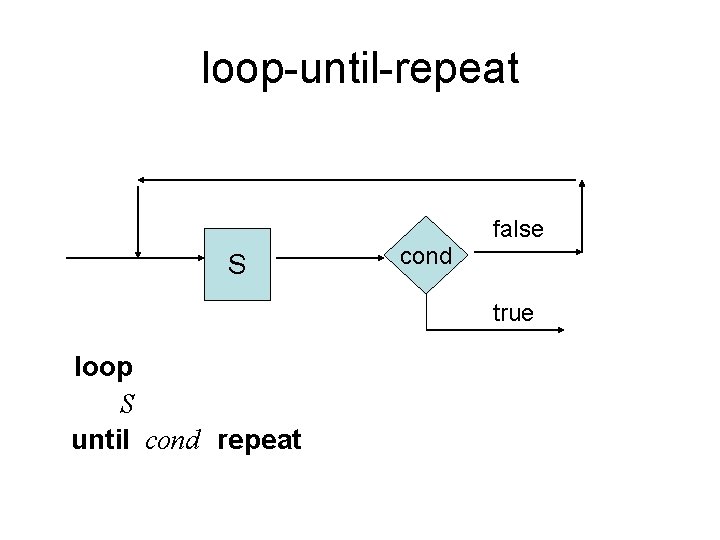
loop-until-repeat false S cond true loop S until cond repeat

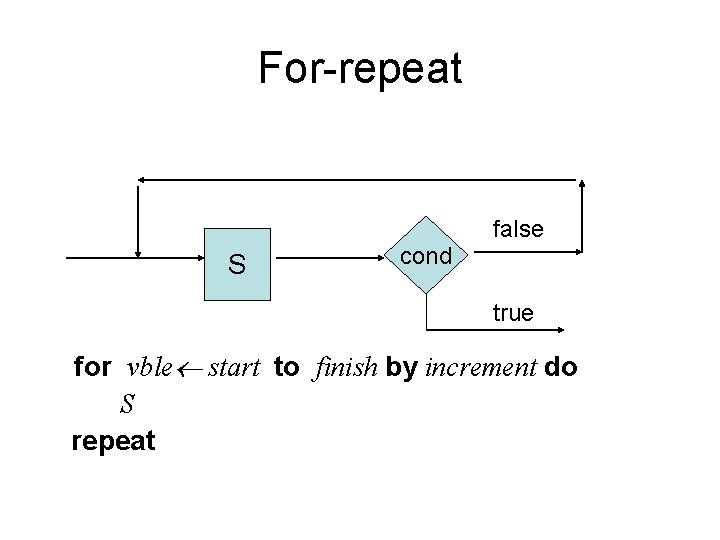
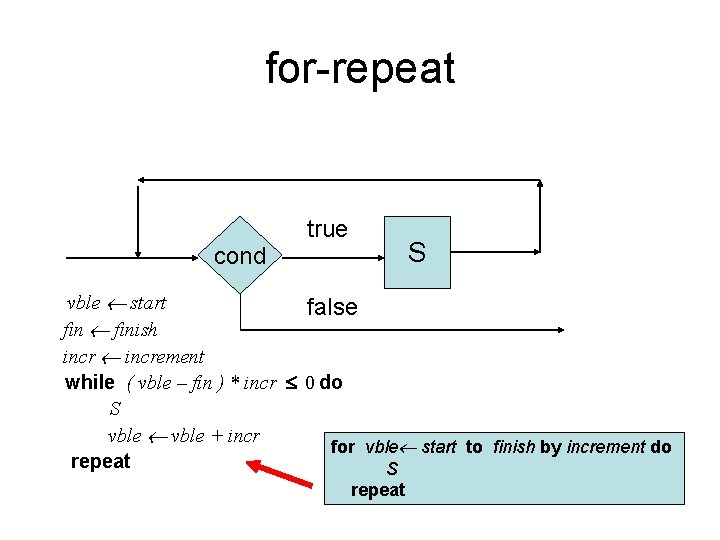
For-repeat false S cond true for vble start to finish by increment do S repeat

for-repeat true S cond vble start false finish increment while ( vble – fin ) * incr 0 do S vble + incr for vble start to finish by increment do repeat S repeat

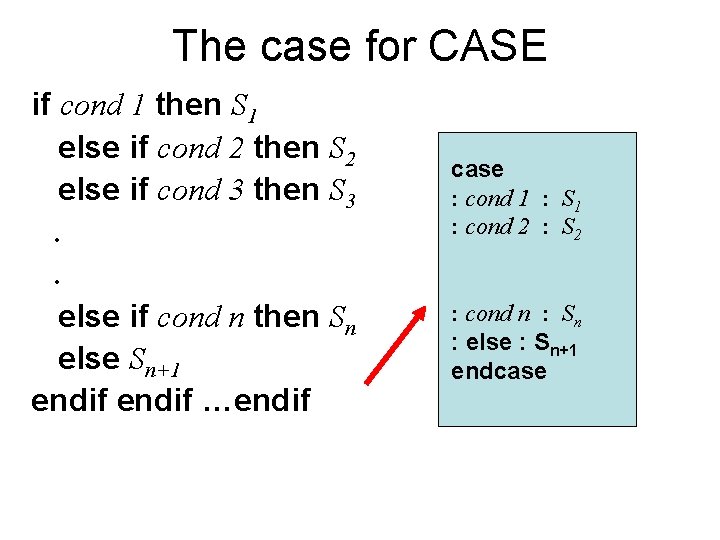
The case for CASE if cond 1 then S 1 else if cond 2 then S 2 else if cond 3 then S 3. . else if cond n then Sn else Sn+1 endif …endif case : cond 1 : S 1 : cond 2 : S 2 : cond n : Sn : else : Sn+1 endcase
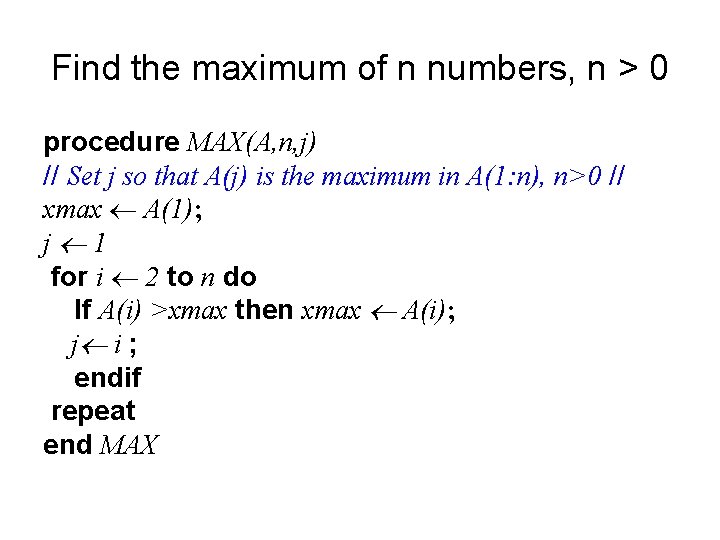
Find the maximum of n numbers, n > 0 procedure MAX(A, n, j) // Set j so that A(j) is the maximum in A(1: n), n>0 // xmax A(1); j 1 for i 2 to n do If A(i) >xmax then xmax A(i); j i ; endif repeat end MAX

Find the maximum of n numbers, n > 0 procedure MAX 1(i) //this is a function which returns the largest integer k such that A(k) is the maximum element in A(i: n)// global integer n, A(1: n), j, k ; integer i if i < n then j MAX 1(i+1) if A(i) >A(j) then k i else k j endif else k n endif return(k) end MAX 1

procedure MAX 2(i) local integer j, k; global integer n, A(1: n); integer i integer STACK(1: 2*n); top 0 L 1: if i < n then top + 1; STACK(top) i top + 1; STACK(top) 2; i i+1 go to L 1 L 2: j STACK(top); top – 1 if A(i) >A(j) then k i else k j endif else k n endif If top=0 then return(k) else addr STACK(top); top – 1 i STACK(top); top – 1 top + 1; STACK(top) k If addr = 2 then go to L 2 endif end MAX 2

procedure MAX 3(A, n) integer i, k, n; i k-n while i>1 do i i-1 if A(i) >A(k) then k i endif repeat return(k) end MAX 3
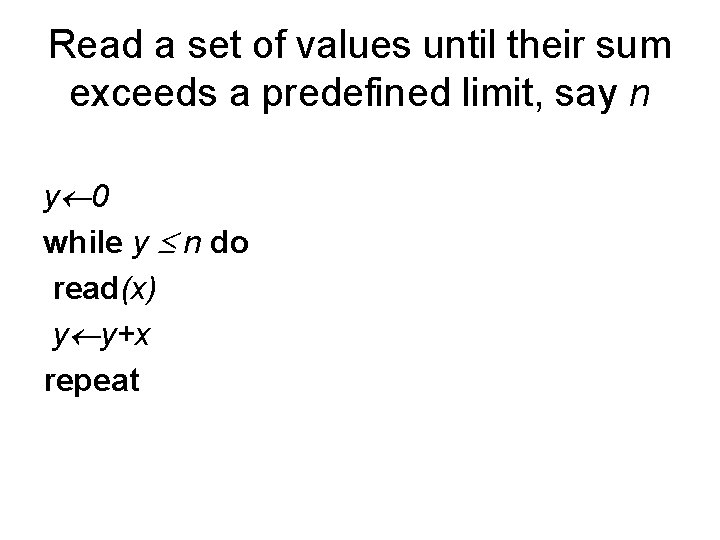
Read a set of values until their sum exceeds a predefined limit, say n y 0 while y n do read(x) y y+x repeat

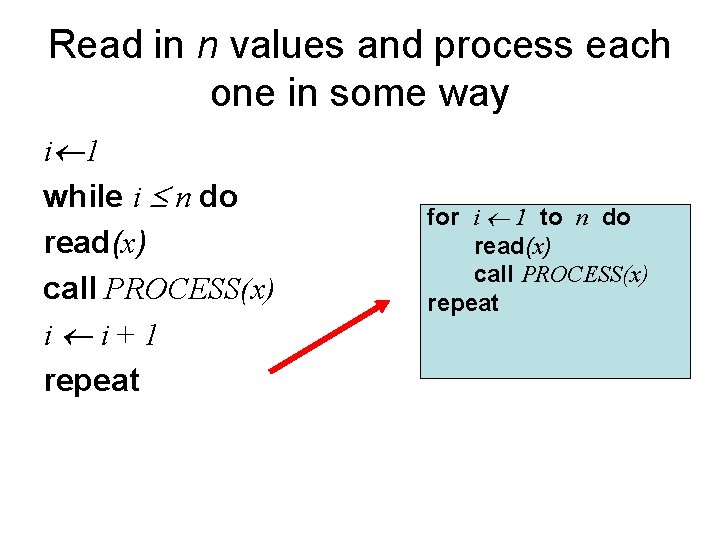
Read in n values and process each one in some way i 1 while i n do read(x) call PROCESS(x) i i+1 repeat for i 1 to n do read(x) call PROCESS(x) repeat

Recursion The fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, … is defined as F 0 = F 1 = 1, Fi = Fi-1 + Fi-2 , i>1 procedure F(n) //returns the nth Fibonacci number// Integer n If n 1 then return(1) else return(F(n-1) + F(n-2)) endif end F

procedure F 1(n) // a function which returns the nth Fibonacci number// If n < 2 then return(1) else return(F 2(2, n, 1, 1)) endif end F 1 procedure F 2(i, n, x, y) If i n then call F 2(i+1, n, y, x+y) endif return(y) end F 2

Computing the greatest common divisor of two nonnegative integers For example : gcd(22, 8)= ? 22 = 1 x 2 x 11 8 = 1 x 23 gcd(22, 8) = 2 Another way : gcd(22, 8)=gcd(8, 6)=gcd(6, 2)=gcd(2, 0)=2

Computing the greatest common divisor of two nonnegative integers For example : gcd(21, 13)= ? 21 = 1 x 3 x 7 13 = 1 x 13 gcd(21, 13) = 1 Another way : gcd(21, 13)=gcd(13, 8)=gcd(8, 5)=gcd(5, 3)= gcd(3, 2)=gcd(2, 1)=gcd(1, 0)=1

Computing the greatest common divisor of two nonnegative integers procedure GCD(a, b) // assume a > b 0 // if b = 0 then return(a) else return(GCD(b, a mod b)) endif end GCD

Computing the greatest common divisor of two nonnegative integers procedure GCD 1(a, b) L 1: if b=0 then return(a) else t b; b a mod b; a t; go to L 1 endif end GCD 1

Computing the greatest common divisor of two nonnegative integers procedure GCD 2(a, b) while b 0 do t b; b a mod b; a t repeat return(a) end GCD 2

A procedure which searches for x in A(1: n) procedure SEARCH(i) //if there exists an index k such that A(k) = x in A(i: n), then the first such k is returned else zero is returned// global n, x, A(1: n) case : i> n : return(0) : A(i) = x : return(i) : else : return(SEARCH(i+1)) endcase end SEARCH

Analyzing Algoriths x x+y 1 for i 1 to n do x x+y repeat n 2

Orders of magnitude • The order of magnitude of a statement refers to its frequency of execution while • The order of magnitude of an algorithm refers to the sum of the frequencies of all of its statements

• Determining the order of magnitude of an algorithm is very important and producing an algorithm which is faster by an order of magnitude is a significant accomplishment. • The a priori analysis of algorithms is concerned chiefly with order of magnitude determination • Fortunately there is a convinient mathematical notation for dealing with this concept. • A priori = berdasarkan teori drpd kenyataan yg sebenarnya
![Insertion Sort InsertionSortA 1 for j 2 to lengthA 2 do key Aj 3 Insertion Sort Insertion-Sort(A) 1 for j 2 to length[A] 2 do key A[j] 3](https://slidetodoc.com/presentation_image_h2/6264d249879031cc3fe04b1dad00c18d/image-26.jpg)
Insertion Sort Insertion-Sort(A) 1 for j 2 to length[A] 2 do key A[j] 3 Insert A[j] into the sorted sequence A[1. . j-1] 4 i j -1 5 while i >0 and A[i]>key do A[i+1] A[i] 6 7 i i -1 8 A[i+1] key cost c 1 c 2 times n n-1 0 c 4 c 5 c 6 c 7 c 8 n-1 tj (tj – 1) n-1

• The running time of the algorithm is the sum of running time for each statement executed; • To compute (n), the running time of Insertion-Sort, we sum the products of the cost and times columns, obtaining (n) = c 1 n + c 2(n-1) + c 4(n-1)+ c 5 tj + c 6 (tj – 1) + c 7 (tj – 1) + c 8(n-1)