The Islamic University of Gaza Faculty of Engineering

The Islamic University of Gaza Faculty of Engineering Civil Engineering Department Numerical Analysis ECIV 3306 Chapter 6 Open Methods

Open Methods • Bracketing methods are based on assuming an interval of the function which brackets the root. • The bracketing methods always converge to the root. • Open methods are based on formulas that require only a single starting value of x or two starting values that do not necessarily bracket the root. • These method sometimes diverge from the true root.

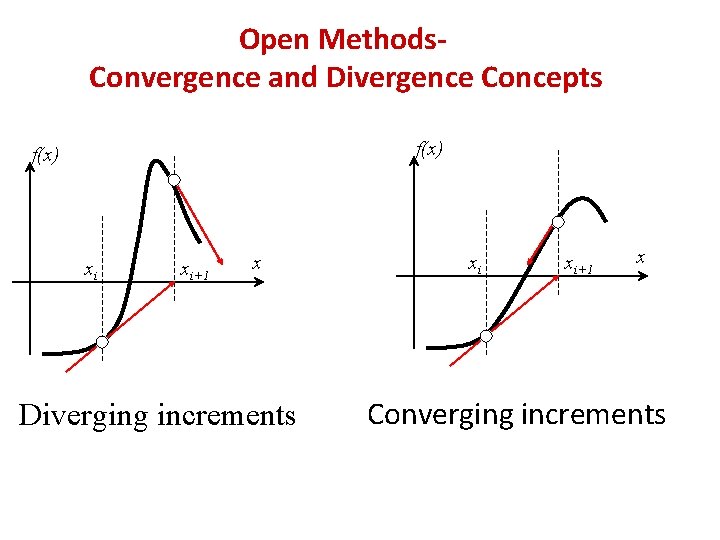
Open Methods. Convergence and Divergence Concepts f(x) xi xi+1 x Diverging increments xi xi+1 x Converging increments

1. Simple Fixed-Point Iteration • Rearrange the function so that x is on the left side of the equation: • Bracketing methods are “convergent”. • Fixed-point methods may sometime “diverge”, depending on the stating point (initial guess) and how the function behaves.

Simple Fixed-Point Iteration Examples: 1. 2. f(x) = x 2 -2 x+3 x = g(x)=(x 2+3)/2 3. f(x) = sin x x = g(x)= sin x + x 3. f(x) = e-x- x x = g(x)= e-x

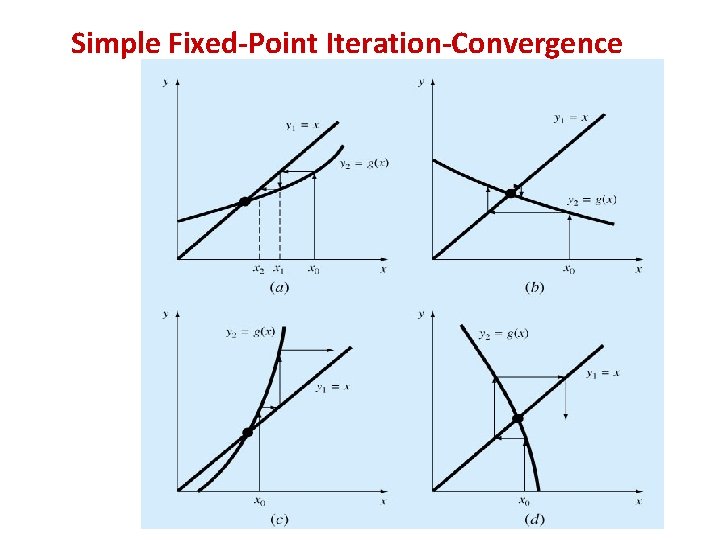
Simple Fixed-Point Iteration Convergence • x = g(x) can be expressed as a pair of equations: y 1= x y 2= g(x)…. (component equations) • Plot them separately.

Simple Fixed-Point Iteration Convergence

Simple Fixed-Point Iteration Convergence Derivative mean value theorem: If g(x) are continuous in [a, b] then there exist at least one value of x= within the interval such that: i. e. there exist one point where the slope parallel to the line joining (a & b)

Simple Fixed-Point Iteration Convergence

Simple Fixed-Point Iteration Convergence • Fixed-point iteration converges if : • When the method converges, the error is roughly proportional to or less than the error of the previous step, therefore it is called “linearly convergent. ”

Simple Fixed-Point Iteration-Convergence

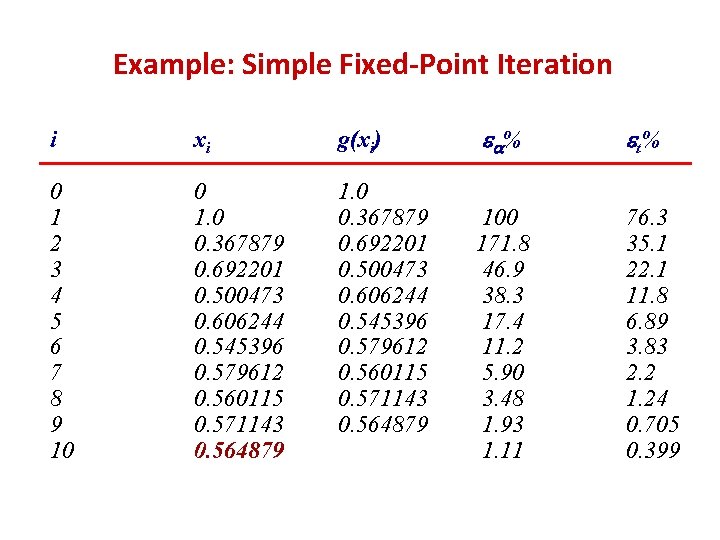
Example: Simple Fixed-Point Iteration f(x) = e-x - x f(x)=e-x - x 1. f(x) is manipulated so that we get x=g(x) = e-x 2. Thus, the formula predicting the new value of x is: xi+1 = e-xi 3. Guess xo = 0 4. The iterations continues till the approx. error reaches a certain limiting value Root f(x) x f 1(x) = x g(x) = e-x x

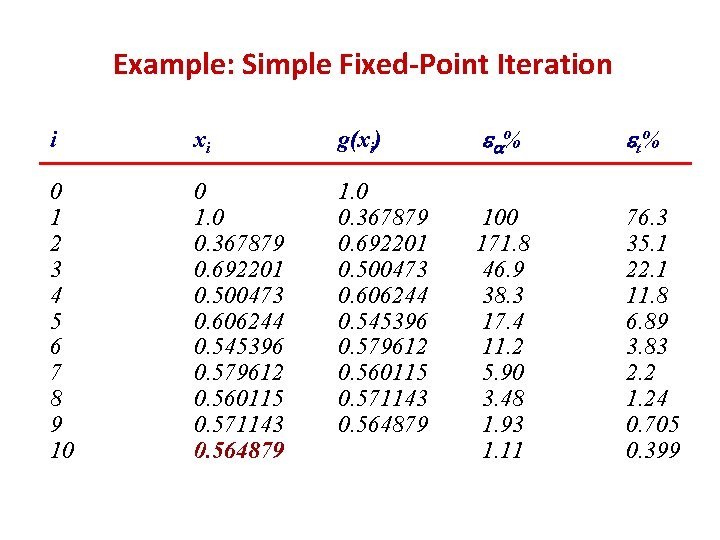
Example: Simple Fixed-Point Iteration i xi g(xi) 0 1 2 3 4 5 6 7 8 9 10 0 1. 0 0. 367879 0. 692201 0. 500473 0. 606244 0. 545396 0. 579612 0. 560115 0. 571143 0. 564879 e a% e t% 100 171. 8 46. 9 38. 3 17. 4 11. 2 5. 90 3. 48 1. 93 1. 11 76. 3 35. 1 22. 1 11. 8 6. 89 3. 83 2. 2 1. 24 0. 705 0. 399

Example: Simple Fixed-Point Iteration i xi g(xi) 0 1 2 3 4 5 6 7 8 9 10 0 1. 0 0. 367879 0. 692201 0. 500473 0. 606244 0. 545396 0. 579612 0. 560115 0. 571143 0. 564879 e a% e t% 100 171. 8 46. 9 38. 3 17. 4 11. 2 5. 90 3. 48 1. 93 1. 11 76. 3 35. 1 22. 1 11. 8 6. 89 3. 83 2. 2 1. 24 0. 705 0. 399

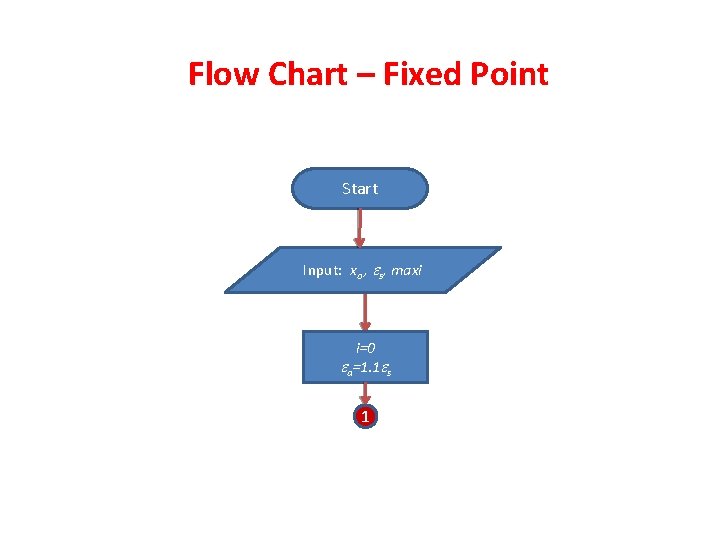
Flow Chart – Fixed Point Start Input: xo , s, maxi i=0 a=1. 1 s 1

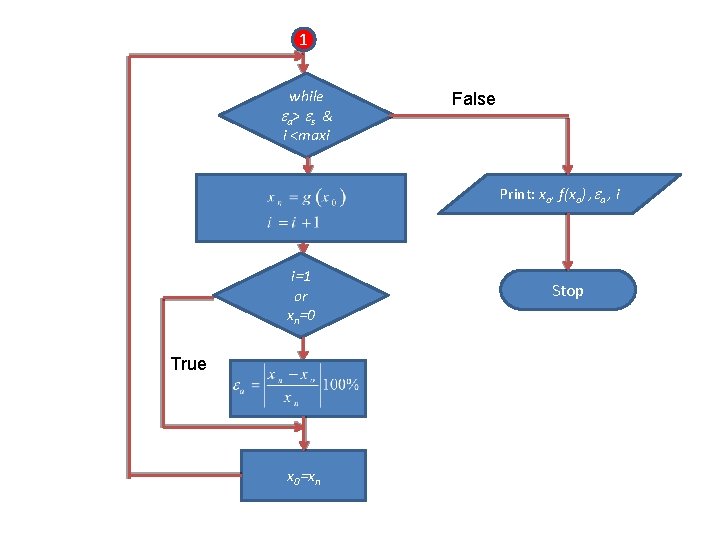
1 while a> s & i <maxi False Print: xo, f(xo) , a , i i=1 or xn=0 True x 0=xn Stop

2. The Newton-Raphson Method • Most widely used method. • Based on Taylor series expansion: Solve for Newton-Raphson formula

The Newton-Raphson Method • • A tangent to f(x) at the initial point xi is extended f(x) till it meets the x-axis at f(xi) the improved estimate of the root xi+1. The iterations continues till the approx. error reaches a certain limiting value. f(x) Slope f /(xi) x Root xi+1 xi

Example: The Newton Raphson Method • Use the Newton-Raphson method to find the root of e-x-x= 0 f(x) = e-x-x and f`(x)= -e-x-1; thus Iter. 0 1 2 3 4 xi 0 0. 566311003 0. 567143165 0. 567143290 e t% 100 11. 8 0. 147 0. 00002 <10 -8

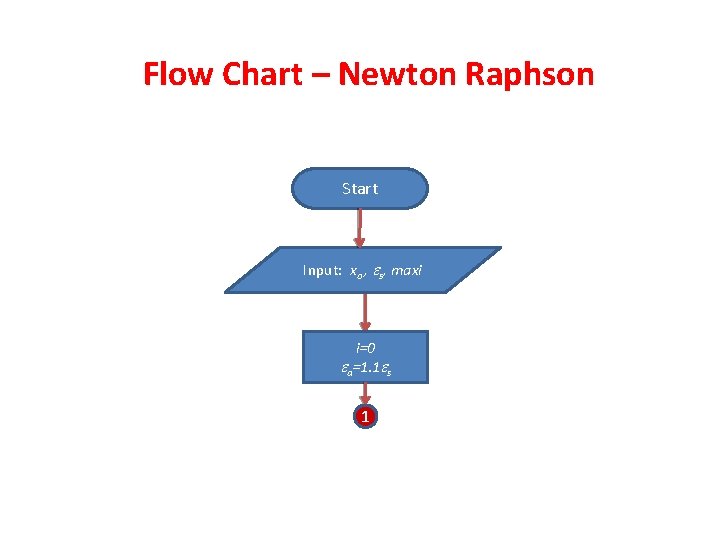
Flow Chart – Newton Raphson Start Input: xo , s, maxi i=0 a=1. 1 s 1

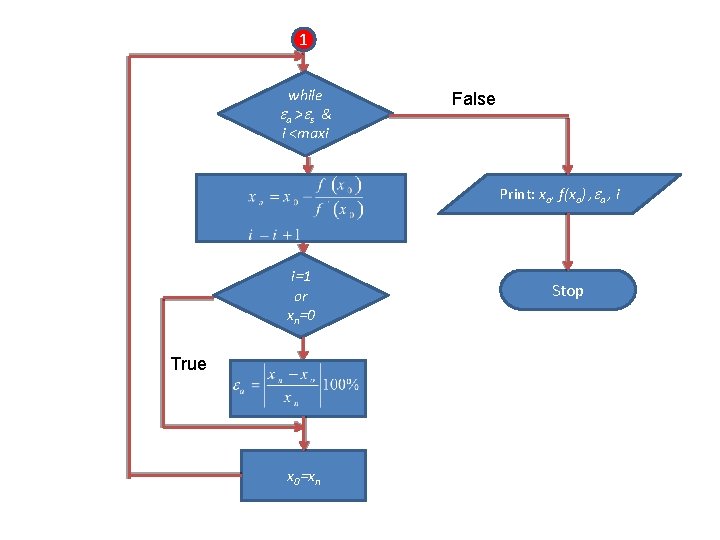
1 while a > s & i <maxi False Print: xo, f(xo) , a , i i=1 or xn=0 True x 0=xn Stop

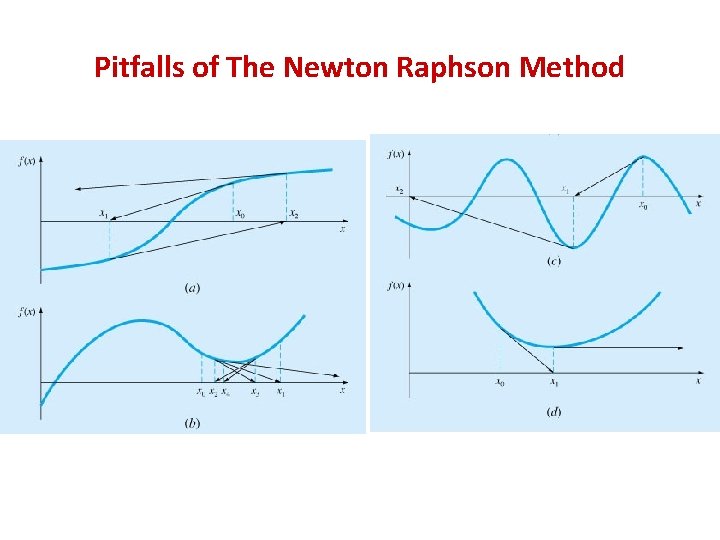
Pitfalls of The Newton Raphson Method

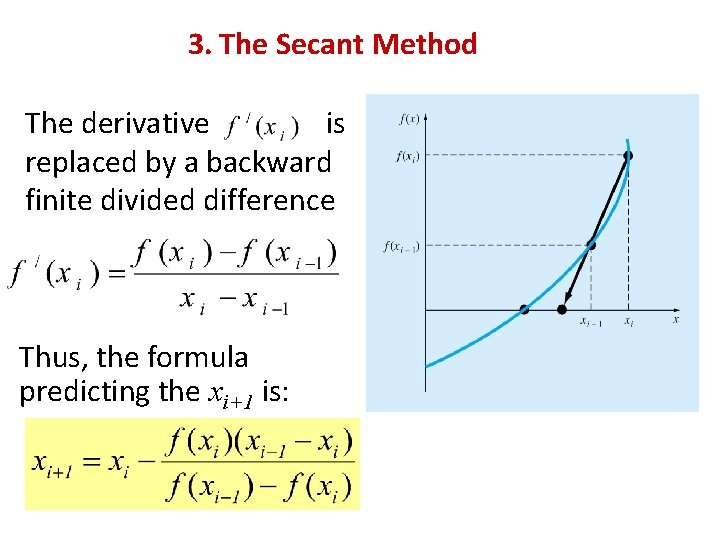
3. The Secant Method The derivative is replaced by a backward finite divided difference Thus, the formula predicting the xi+1 is:

The Secant Method • Requires two initial estimates of x , e. g, x o, x 1. However, because f(x) is not required to change signs between estimates, it is not classified as a “bracketing” method. • The scant method has the same properties as Newton’s method. Convergence is not guaranteed for all xo, x 1, f(x).

Secant Method: Example • Use the Secant method to find the root of e-x-x=0; f(x) = e-x-x and xi-1=0, x 0=1 to get x 1 of the first iteration using: Iter 1 2 3 xi-1 0 1. 0 0. 613 f(xi-1) 1. 0 -0. 632 -0. 0708 xi f(xi) 1. 0 -0. 632 0. 613 -0. 0708 0. 5638 0. 00518 xi+1 0. 613 0. 5638 0. 5672 e t% 8. 0 0. 58 0. 0048

Comparison of convergence of False Position and Secant Methods False Position Secant Method Use two estimate xl and xu Use two estimate xi and xi-1 f(x) must changes signs between xl f(x) is not required to change signs between xi and xi-1 and xu Xr replaces whichever of the original values yielded a function value with the same sign as f(xr) Xi+1 replace xi Xi replace xi-1 Always converge May be diverge

Comparison of convergence of False Position and Secant Methods • Use the false-position and secant method to find the root of f(x)=lnx. Start computation with xl= xi-1=0. 5, xu=xi = 5. 1. False position method Iter 1 2 3 xl xu 0. 5 5. 0 1. 8546 1. 2163 xr 1. 8546 1. 2163 1. 0585 Secant method 2. Iter xi-1 xi 1 0. 5 5. 0 2 5 1. 8546 xi+1 1. 8546 -0. 10438

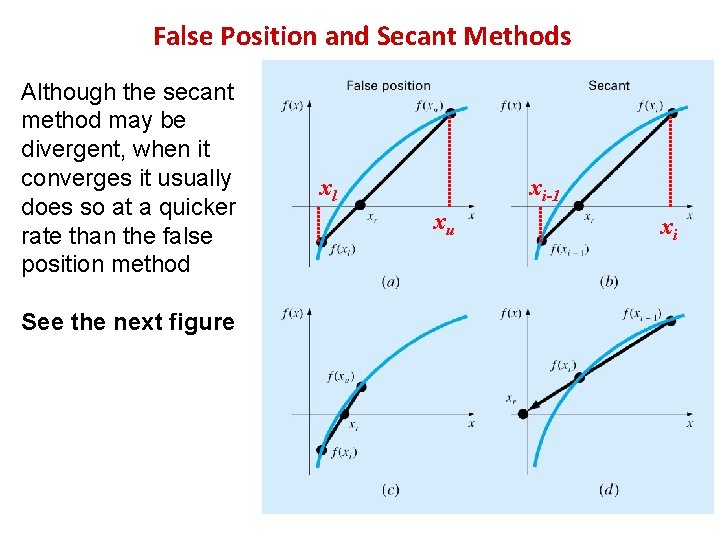
False Position and Secant Methods Although the secant method may be divergent, when it converges it usually does so at a quicker rate than the false position method See the next figure xl xi-1 xu xi

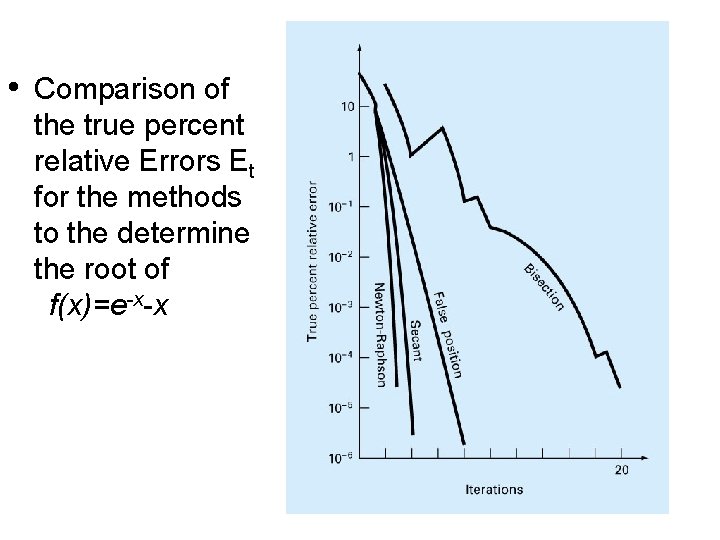
• Comparison of the true percent relative Errors Et for the methods to the determine the root of f(x)=e-x-x

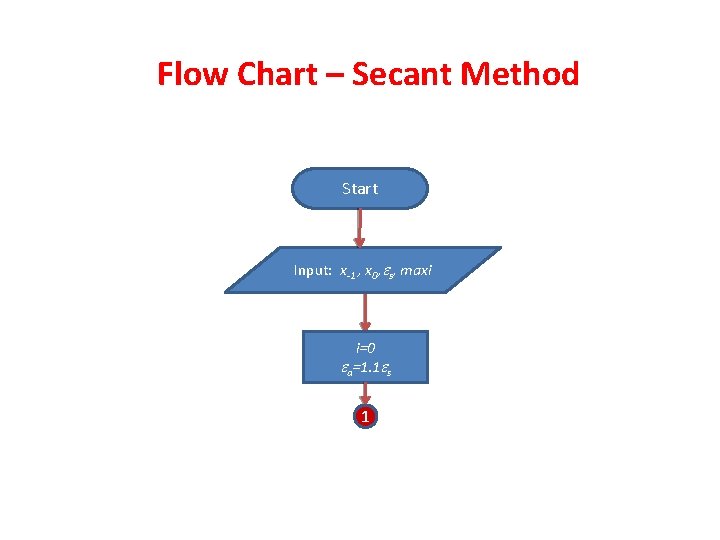
Flow Chart – Secant Method Start Input: x-1 , x 0, s, maxi i=0 a=1. 1 s 1

1 while a > s & i < maxi False Print: xi , f(xi) , a , i i=1 or Xi+1=0 True Xi-1=xi Xi=xi+1 Stop

Modified Secant Method Rather than using two initial values, an alternative approach is using a fractional perturbation of the independent variable to estimate is a small perturbation fraction

Modified Secant Method: Example • Use the modified secant method to find the root of f(x) = e-x-x and, x 0=1 and =0. 01

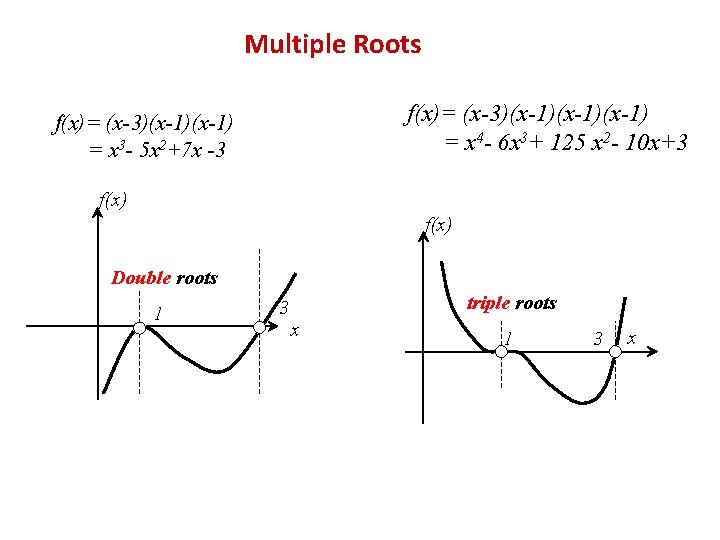
Multiple Roots f(x)= (x-3)(x-1)(x-1) = x 4 - 6 x 3+ 125 x 2 - 10 x+3 f(x)= (x-3)(x-1) = x 3 - 5 x 2+7 x -3 f(x) Double roots 1 3 triple roots x 1 3 x

Multiple Roots • “Multiple root” corresponds to a point where a function is tangent to the x axis. • Difficulties - Function does not change sign with double (or even number of multiple root), therefore, cannot use bracketing methods. - Both f(x) and f′(x)=0, division by zero with Newton’s and Secant methods which may diverge around this root.

4. The Modified Newton Raphson Method • Another u(x) is introduced such that u(x)=f(x)/f /(x); • Getting the roots of u(x) using Newton Raphson technique: This function has roots at all the same locations as the original function

Modified Newton Raphson Method: Example Using the Newton Raphson and Modified Newton Raphson evaluate the multiple roots of f(x)= x 3 -5 x 2+7 x-3 with an initial guess of x 0=0 • Newton Raphson formula: • Modified Newton Raphson formula:

Modified Newton Raphson Method: Example Newton Raphson Iter xi 0 0 1 0. 4286 2 0. 6857 3 0. 83286 17 4 0. 91332 8. 7 5 0. 95578 4. 4 6 0. 97766 2. 2 t% 100 57 31 Modified Newton-Raphson iter xi t% 0 0 100 1 1. 10526 11 2 1. 00308 0. 31 3 1. 0000024 • Newton Raphson technique is linearly converging towards the true value of 1. 0 while the Modified Newton Raphson is quadratically converging. • For simple roots, modified Newton Raphson is less efficient and requires more computational effort than the standard Newton Raphson method

Systems of Nonlinear Equations • Roots of a set of simultaneous equations: f 1(x 1, x 2, ……. , xn)=0 f 2 (x 1, x 2, ……. , xn)=0 fn (x 1, x 2, ……. , xn)=0 • The solution is a set of x values that simultaneously get the equations to zero.

Systems of Nonlinear Equations Example: x 2 + xy = 10 & y + 3 xy 2 = 57 u(x, y) = x 2+ xy -10 = 0 v(x, y) = y+ 3 xy 2 -57 = 0 • The solution will be the value of x and y which makes u(x, y)=0 and v(x, y)=0 • These are x=2 and y=3 • Numerical methods used are extension of the open methods for solving single equation; Fixed point iteration and Newton-Raphson.

Systems of Nonlinear Equations: 1. Fixed Point Iteration 1. 2. Use an initial guess x =1. 5 and y =3. 5 The iteration formulae: xi+1=(10 -xi 2)/yi 3. and yi+1=57 -3 xiyi 2 First iteration, x=(10 -(1. 5)2)/3. 5=2. 21429 y=(57 -3(2. 21429)(3. 5)2=-24. 37516 4. Second iteration: x=(10 -2. 214292)/-24. 37516=-0. 209 y=57 -3(-0. 209)(-24. 37516)2=429. 709 5. Solution is diverging so try another iteration formula

Systems of Nonlinear Equations: 1. Fixed Point Iteration 1. Using iteration formula: xi+1=(10 -xiyi)1/2 and yi+1=[(57 -yi)/3 xi]1/2 First guess: x=1. 5 and y=3. 5 2. 1 st iteration: x=(10 -(1. 5)(3. 5))1/2=2. 17945 y=((57 -(3. 5))/3(2. 17945))1/2=2. 86051 3. 2 nd iteration: x=(10 -(2. 17945)(2. 86051))1/2=1. 94053 y=((57 -(2. 86051))/3(1. 94053))1/2=3. 04955 4. The approach is converging to the true root, x=2 and y=3

Systems of Nonlinear Equations: 1. Fixed Point Iteration The sufficient condition for convergence for the two-equation case (u(x, y)=0 and v(x, y)=0) are:

Systems of Nonlinear Equations: 2. Newton Raphson Method • Recall the standard Newton Raphson formula: • which can be written as the following formula

Systems of Nonlinear Equations: 2. Newton Raphson Method • By multi-equation version (in this section we deal only with two equation) the formula can be derived in an identical fashion: • u(x, y)=0 and v(x, y)=0

Systems of Nonlinear Equations: 2. Newton Raphson Method • And thus

Systems of Nonlinear Equations: 2. Newton Raphson Method • x 2+ xy =10 and y + 3 xy 2 = 57 are two nonlinear simultaneous equations with two unknown x and y they can be expressed in the form: