VECTORES REPRESENTACIN DE FUERZAS Hay dos tipos de

VECTORES

REPRESENTACIÓN DE FUERZAS Hay dos tipos de magnitudes: ESCALARES y VECTORIALES Las magnitudes ESCALARES quedan determinadas mediante una cantidad y su unidad correspondiente: L (Longitud) = 12’ 35 m m (Masa) = 5’ 678 kg d (Densidad) = 3’ 4 g/cm 3 Las magnitudes VECTORIALES necesitan de otras características más: velocidad, aceleración, fuerzas, etc. Por ello, se representan mediante VECTORES (segmentos de recta que están orientados). Encima del símbolo de la magnitud dibujaremos una pequeña flecha para indicar que se trata de una magnitud vectorial:

CARACTERÍSTICAS DE UN VECTOR Las características de un vector son cuatro: § MÓDULO § DIRECCIÓN § SENTIDO § PUNTO DE APLICACIÓN

MÓDULO El MÓDULO viene dado por la longitud de la flecha. El módulo es proporcional a la intensidad de la fuerza. Al representar las fuerzas usaremos una escala similar a la utilizada en los mapas, por ejemplo, 1 centímetro en el papel equivaldrá a 1 Newton de fuerza (1 cm: 1 N). Escala Þ 1 cm : 2 N 3 cm. 2 N 1 cm = 6 N

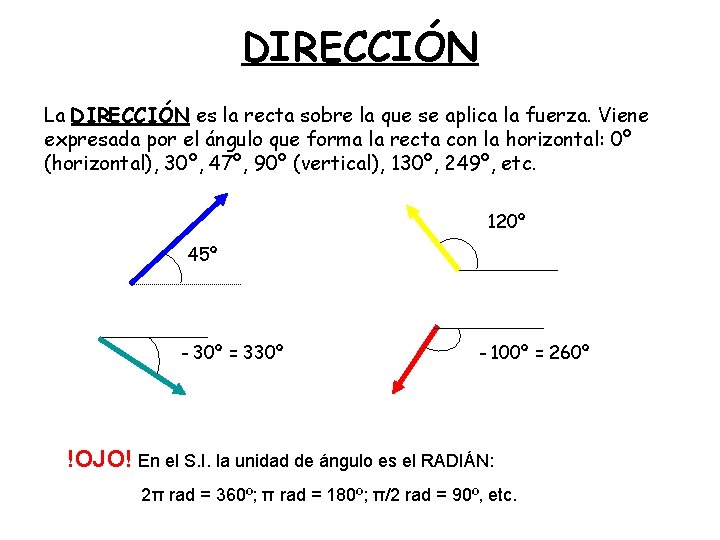
DIRECCIÓN La DIRECCIÓN es la recta sobre la que se aplica la fuerza. Viene expresada por el ángulo que forma la recta con la horizontal: 0º (horizontal), 30º, 47º, 90º (vertical), 130º, 249º, etc. 120º 45º - 30º = 330º - 100º = 260º !OJO! En el S. I. la unidad de ángulo es el RADIÁN: 2π rad = 360º; π rad = 180º; π/2 rad = 90º, etc.

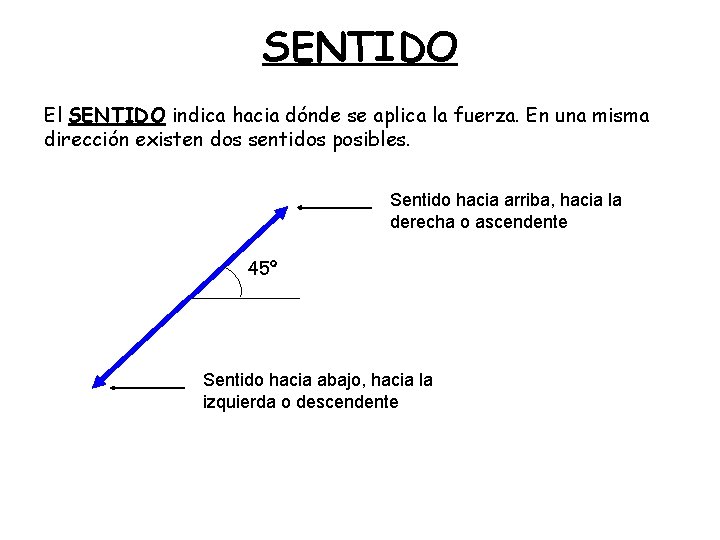
SENTIDO El SENTIDO indica hacia dónde se aplica la fuerza. En una misma dirección existen dos sentidos posibles. Sentido hacia arriba, hacia la derecha o ascendente 45º Sentido hacia abajo, hacia la izquierda o descendente

PUNTO DE APLICACIÓN El PUNTO DE APLICACIÓN es el punto del espacio en que se aplica la fuerza. Esto es importante, pues los efectos que producen las fuerzas dependen en muchos casos del punto de aplicación. FLuna, Tierra = FTierra, Luna Ambas fuerzas tienen el mismo módulo, pero difieren en su PUNTO DE APLICACIÓN.

TRIGONOMETRIA

• Trigonometría se refiere a la medida de los lados y los ángulos de un triángulo. – Aplicaciones de la TRIGONOMETRIA: topografía, navegación e ingeniería. • Podemos desarrollar el tema de trigonometría por medio de dos enfoques, éstos son: – El círculo – El triángulo rectángulo

Trigonometría Enfocada por medio del TRIANGULO RECTANGULO

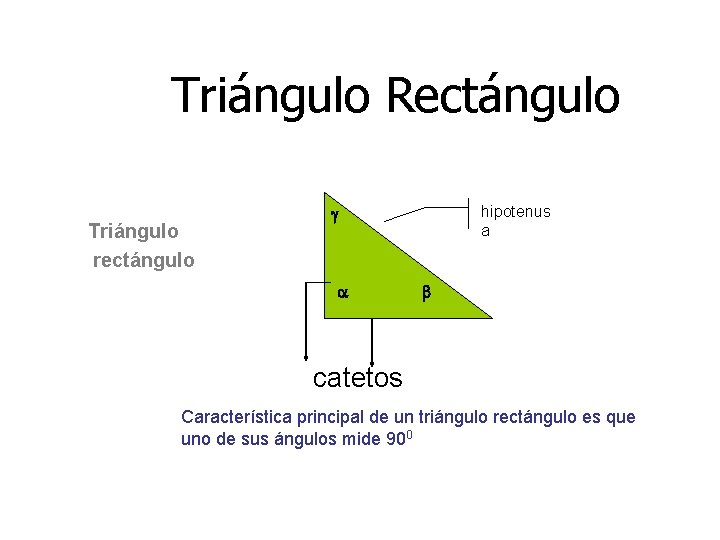
Triángulo Rectángulo Triángulo rectángulo hipotenus a catetos Característica principal de un triángulo rectángulo es que uno de sus ángulos mide 900

Observaciones importantes sobre los triángulos rectángulos. Ø Un triángulo consta de tres lados y de tres ángulos. Ø La suma de los tres ángulos es 1800 Ø La suma de la longitud de cualquiera de dos de los lados del triángulo es mayor que la longitud del tercer lado. Ø Sea c la hipotenusa, a y b los catetos, entonces c 2 = a 2 + b 2

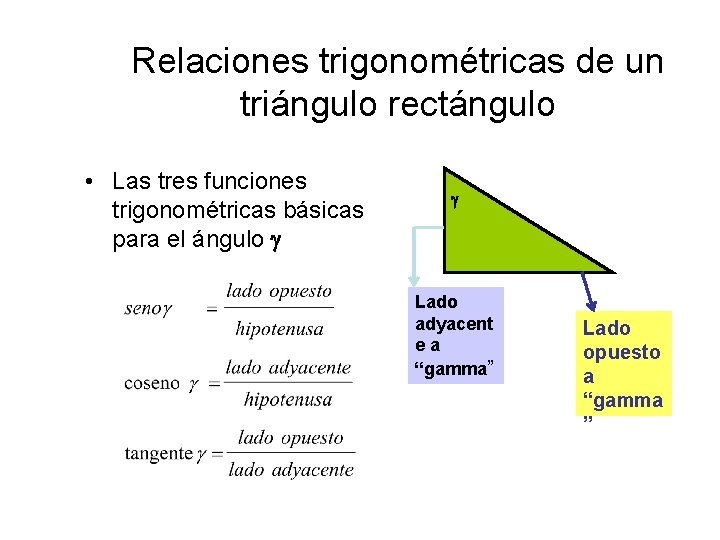
Ø Los ángulos se nombran con letras para identificarlos. Algunas de las letras que utilizamos son del alfabeto griego como por ejemplo; “gamma”; “alpha” ; “betha”

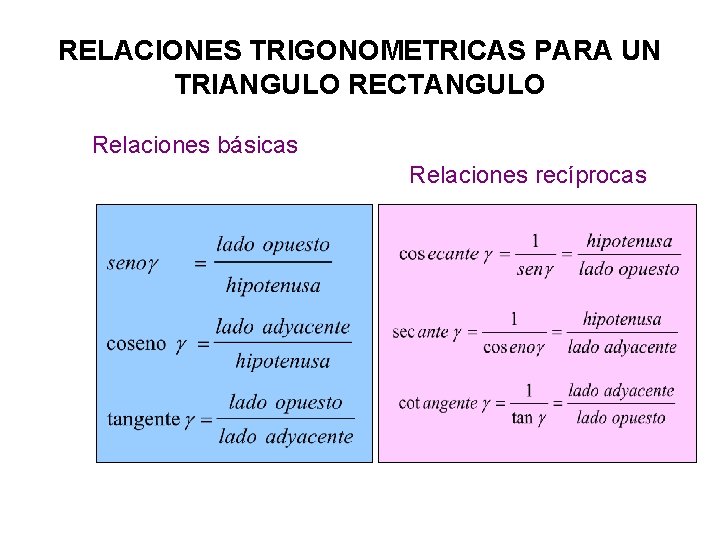
• Podemos relacionar los lados de un triángulo rectángulo con sus ángulos por medio de las relaciones trigonométricas. • Por medio de éstas relaciones trigonométricas podemos hallar información sobre ya sea un lado o un ángulo que desconocemos del triángulo. • Las relaciones trigonométricas son seis, tres de ellas son fundamentales ya que dan origen a las otras.

RELACIONES TRIGONOMETRICAS PARA UN TRIANGULO RECTANGULO Relaciones básicas Relaciones recíprocas

Relaciones trigonométricas de un triángulo rectángulo • Las tres funciones trigonométricas básicas para el ángulo Lado adyacent ea “gamma” Lado opuesto a “gamma ”

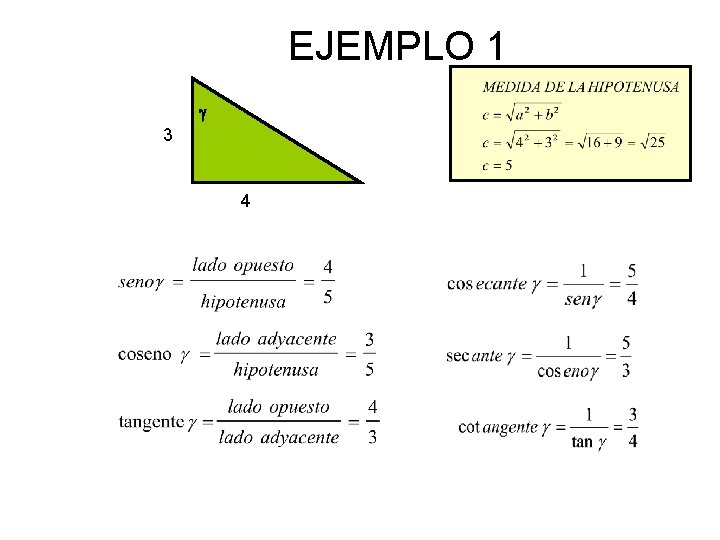
EJEMPLO 1 3 4

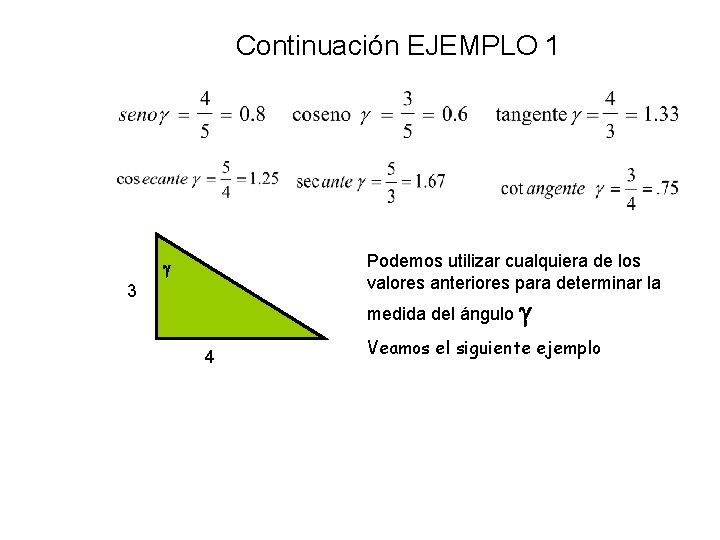
Continuación EJEMPLO 1 Podemos utilizar cualquiera de los valores anteriores para determinar la 3 medida del ángulo 4 Veamos el siguiente ejemplo

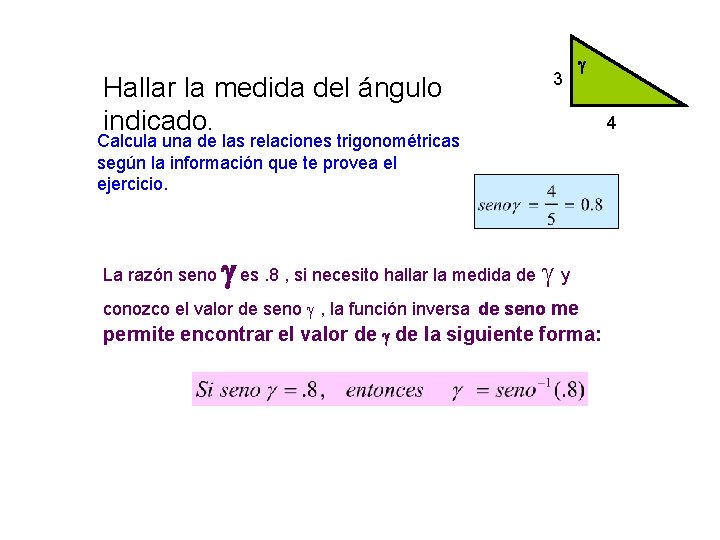
Hallar la medida del ángulo indicado. 3 Calcula una de las relaciones trigonométricas según la información que te provea el ejercicio. La razón seno es. 8 , si necesito hallar la medida de y conozco el valor de seno , la función inversa de seno me permite encontrar el valor de la siguiente forma: 4

CALCULAR LA INVERSA DE SENO Presenta la respuesta en : Grados___ Utilizaremos la calculadora ENTRADA EN LA CALCULADORA. 8 SEN-1 =

ENTRADA EN LA CALCULADORA. 8 SEN-1 = Pantalla Grado 53. 13 Recuerda escoger en tu calculadora la unidad de medida para el ángulo, (grados o radianes) antes de hacer los cómputos.

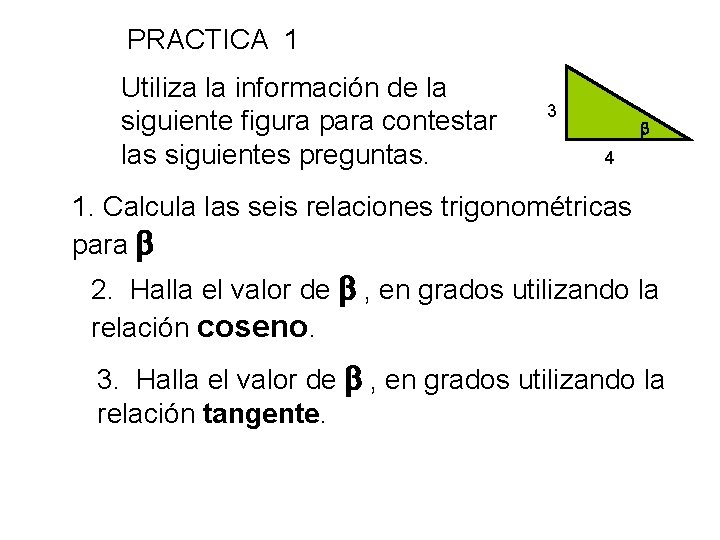
PRACTICA 1 Utiliza la información de la siguiente figura para contestar las siguientes preguntas. 3 4 1. Calcula las seis relaciones trigonométricas para 2. Halla el valor de , en grados utilizando la relación coseno. 3. Halla el valor de , en grados utilizando la relación tangente.

Respuestas -PRACTICA 1 1. Calcula las seis relaciones trigonométricas para 2. Halla el valor de , en grados, utilizando la relación coseno. 3. Halla el valor de , en grados, utilizando la relación tangente.

Compara las relaciones trigonométricas seno y coseno de y =53. 130 = 36. 870 La suma de y es 900 Por tanto y son ángulos complementarios.

Sean y dos ángulos complementarios, entonces, encontramos las siguientes relaciones:

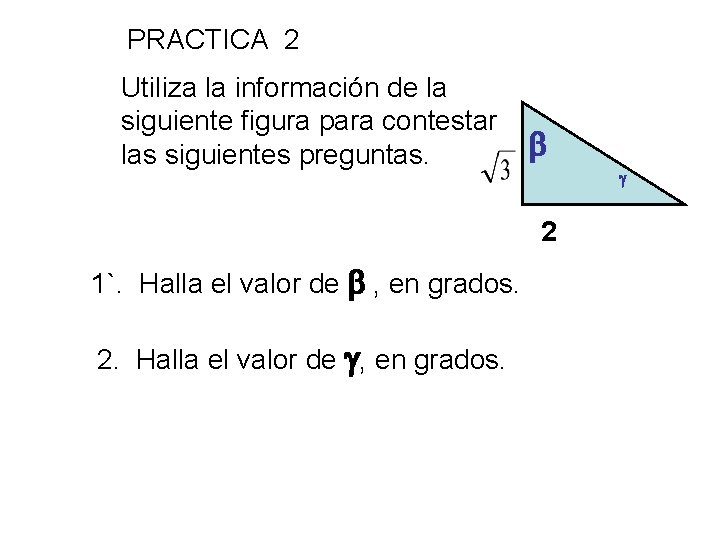
PRACTICA 2 Utiliza la información de la siguiente figura para contestar las siguientes preguntas. 2 2 1`. Halla el valor de , en grados. 2. Halla el valor de , en grados.

Respuestas -PRACTICA 2 1. Halla el valor de , en grados y en radianes. 2. Halla el valor de , en grados y en radianes. En la forma corta tenemos que + = 90, Por lo tanto = 90 - = 90 -49. 11=40. 89 Utilizando las relaciones trigonométricas tenemos

Observación Si conozco dos de los lados de un triángulo rectángulo puedo hallar la medida de sus ángulos.

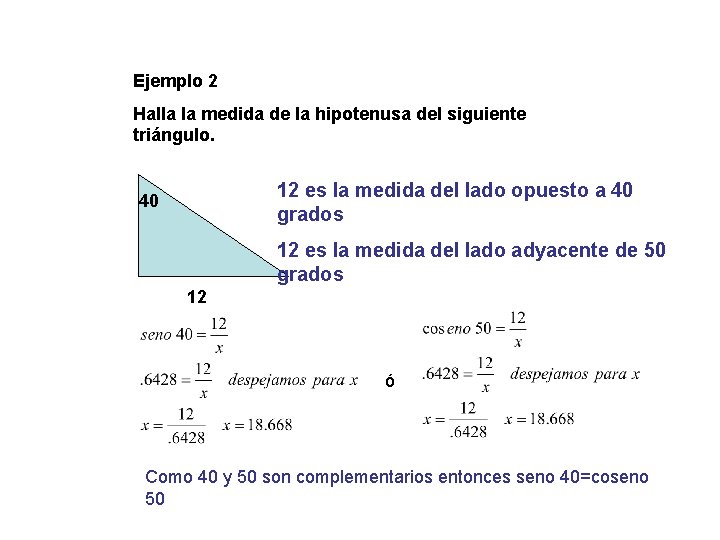
Ejemplo 2 Halla la medida de la hipotenusa del siguiente triángulo. 12 es la medida del lado opuesto a 40 grados 40 12 es la medida del lado adyacente de 50 grados 12 ó Como 40 y 50 son complementarios entonces seno 40=coseno 50

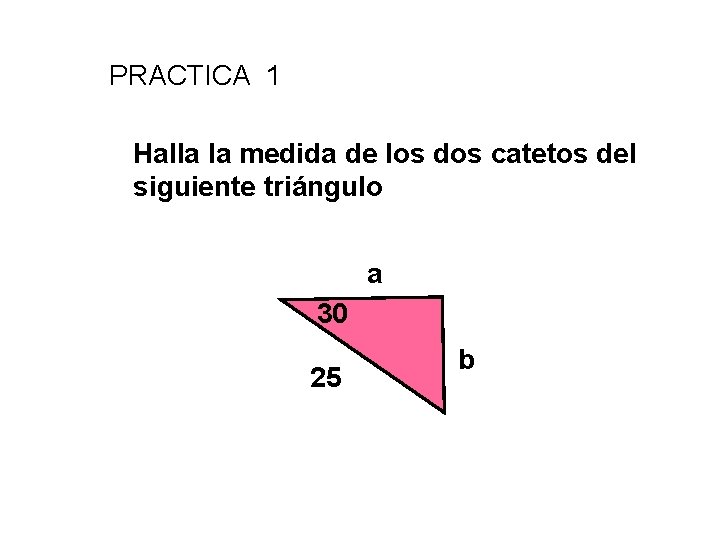
PRACTICA 1 Halla la medida de los dos catetos del siguiente triángulo a 30 25 b

Respuestas-PRACTICA 1 Halla la medida de los dos catetos del siguiente triángulo a 30 25 b

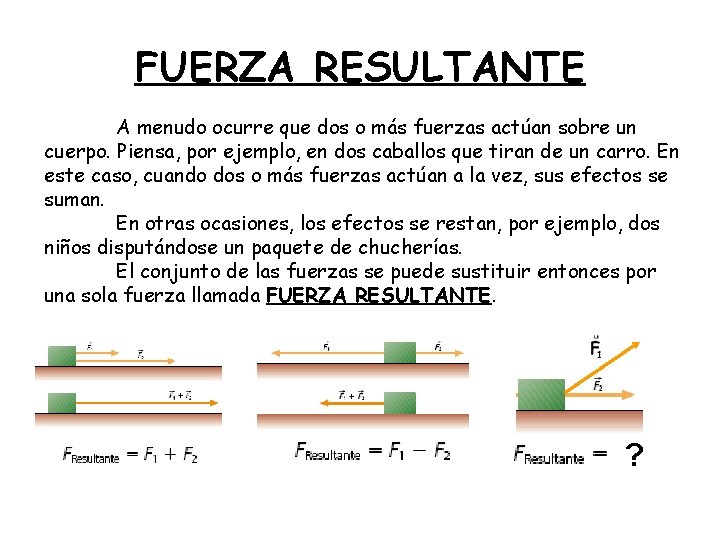
FUERZA RESULTANTE A menudo ocurre que dos o más fuerzas actúan sobre un cuerpo. Piensa, por ejemplo, en dos caballos que tiran de un carro. En este caso, cuando dos o más fuerzas actúan a la vez, sus efectos se suman. En otras ocasiones, los efectos se restan, por ejemplo, dos niños disputándose un paquete de chucherías. El conjunto de las fuerzas se puede sustituir entonces por una sola fuerza llamada FUERZA RESULTANTE. ?

COMPOSICIÓN DE FUERZAS A continuación estudiaremos la manera de calcular la fuerza resultante para el caso de varias fuerzas aplicadas en la misma dirección y para el caso de fuerzas aplicadas en direcciones diferentes. Es lo que se denomina COMPOSICIÓN DE FUERZAS. Vamos a distinguir varias situaciones: a) Misma dirección a. 1) Mismo sentido a. 2) Sentidos contrarios b) Distinta dirección b. 1) Perpendiculares b. 2) No perpendiculares c) Paralelas c. 1) Igual sentido c. 2) Sentidos contrarios

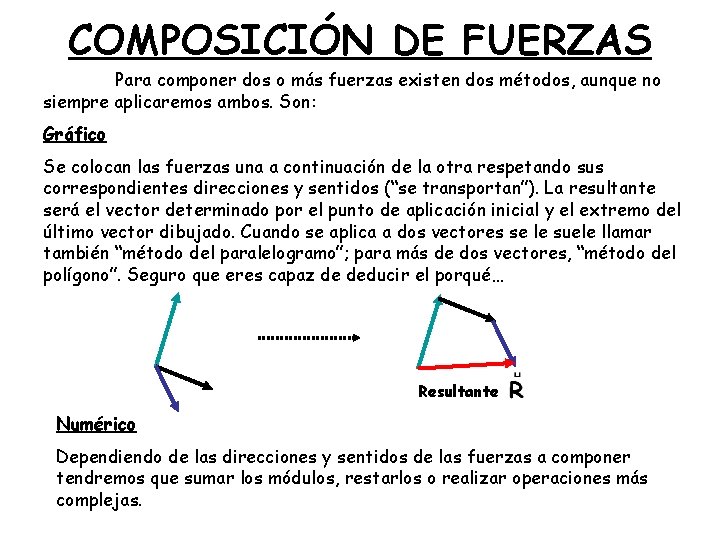
COMPOSICIÓN DE FUERZAS Para componer dos o más fuerzas existen dos métodos, aunque no siempre aplicaremos ambos. Son: Gráfico Se colocan las fuerzas una a continuación de la otra respetando sus correspondientes direcciones y sentidos (“se transportan”). La resultante será el vector determinado por el punto de aplicación inicial y el extremo del último vector dibujado. Cuando se aplica a dos vectores se le suele llamar también “método del paralelogramo”; para más de dos vectores, “método del polígono”. Seguro que eres capaz de deducir el porqué… Resultante Numérico Dependiendo de las direcciones y sentidos de las fuerzas a componer tendremos que sumar los módulos, restarlos o realizar operaciones más complejas.

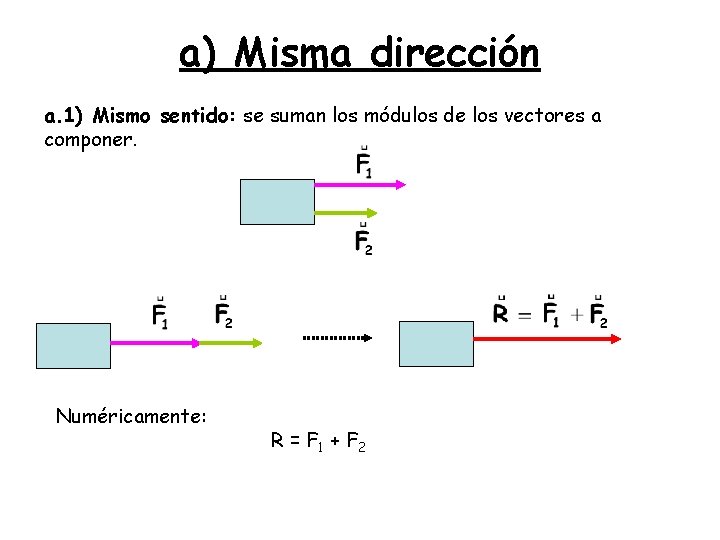
a) Misma dirección a. 1) Mismo sentido: se suman los módulos de los vectores a componer. Numéricamente: R = F 1 + F 2

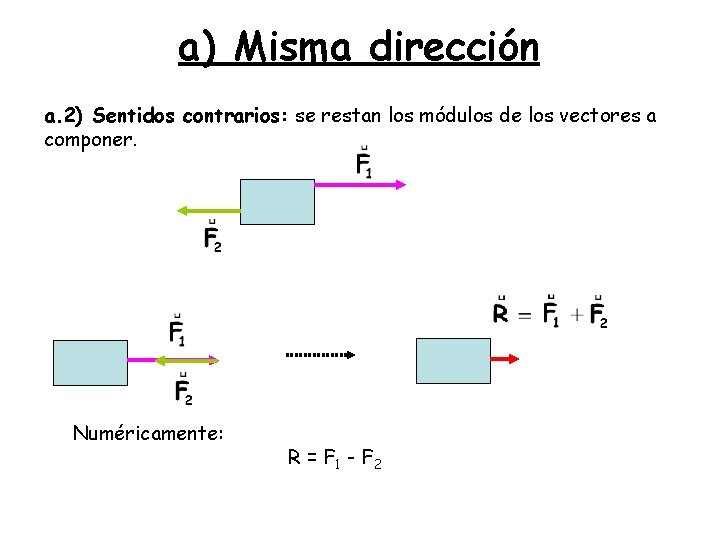
a) Misma dirección a. 2) Sentidos contrarios: se restan los módulos de los vectores a componer. Numéricamente: R = F 1 - F 2

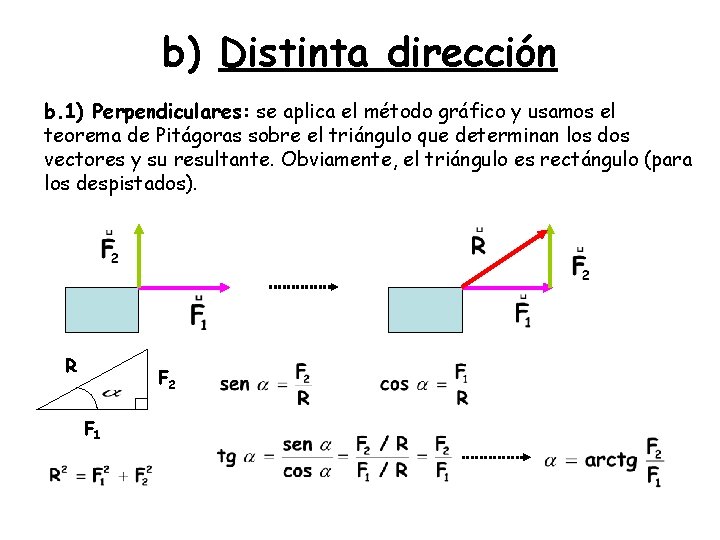
b) Distinta dirección b. 1) Perpendiculares: se aplica el método gráfico y usamos el teorema de Pitágoras sobre el triángulo que determinan los dos vectores y su resultante. Obviamente, el triángulo es rectángulo (para los despistados). R F 2 F 1

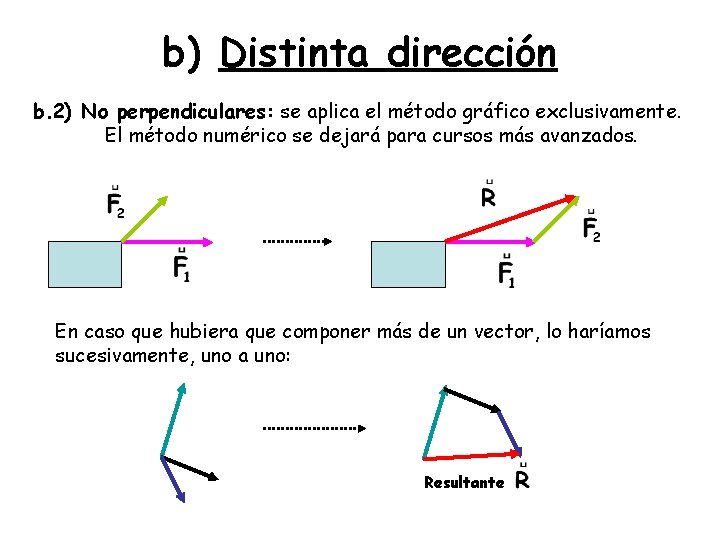
b) Distinta dirección b. 2) No perpendiculares: se aplica el método gráfico exclusivamente. El método numérico se dejará para cursos más avanzados. En caso que hubiera que componer más de un vector, lo haríamos sucesivamente, uno a uno: Resultante

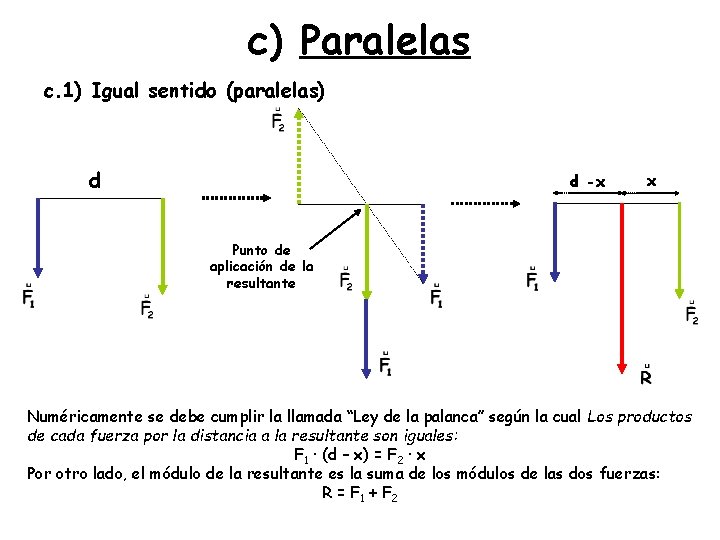
c) Paralelas c. 1) Igual sentido (paralelas) d d -x x Punto de aplicación de la resultante Numéricamente se debe cumplir la llamada “Ley de la palanca” según la cual Los productos de cada fuerza por la distancia a la resultante son iguales: F 1 · (d – x) = F 2 · x Por otro lado, el módulo de la resultante es la suma de los módulos de las dos fuerzas: R = F 1 + F 2

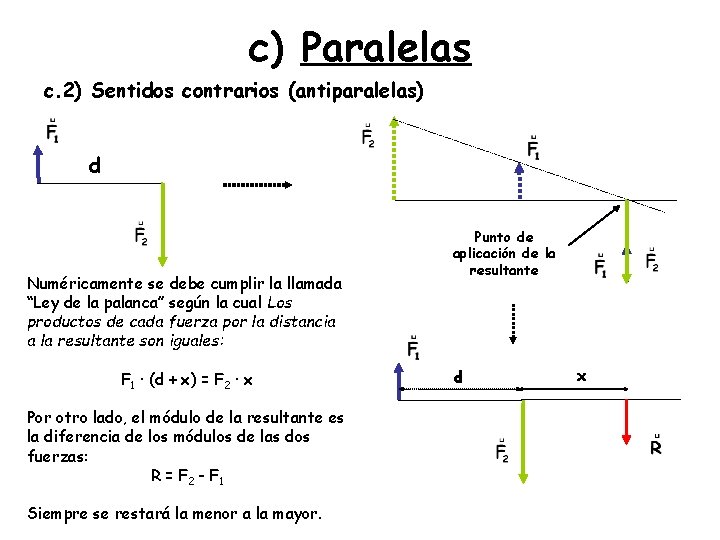
c) Paralelas c. 2) Sentidos contrarios (antiparalelas) d Numéricamente se debe cumplir la llamada “Ley de la palanca” según la cual Los productos de cada fuerza por la distancia a la resultante son iguales: F 1 · (d + x) = F 2 · x Por otro lado, el módulo de la resultante es la diferencia de los módulos de las dos fuerzas: R = F 2 - F 1 Siempre se restará la menor a la mayor. Punto de aplicación de la resultante d x

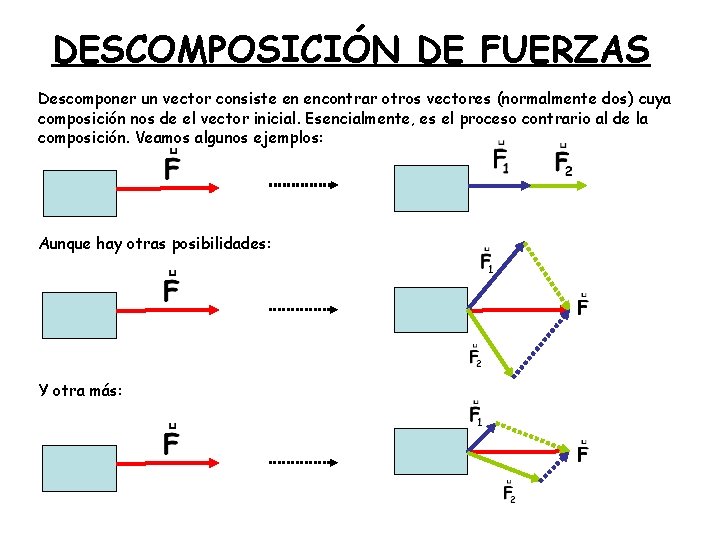
DESCOMPOSICIÓN DE FUERZAS Descomponer un vector consiste en encontrar otros vectores (normalmente dos) cuya composición nos de el vector inicial. Esencialmente, es el proceso contrario al de la composición. Veamos algunos ejemplos: Aunque hay otras posibilidades: Y otra más:

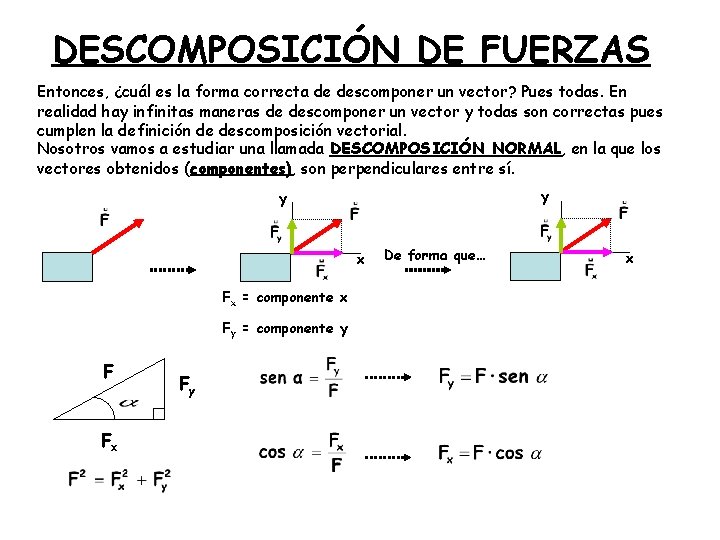
DESCOMPOSICIÓN DE FUERZAS Entonces, ¿cuál es la forma correcta de descomponer un vector? Pues todas. En realidad hay infinitas maneras de descomponer un vector y todas son correctas pues cumplen la definición de descomposición vectorial. Nosotros vamos a estudiar una llamada DESCOMPOSICIÓN NORMAL, en la que los vectores obtenidos (componentes), son perpendiculares entre sí. y y x Fx = componente x Fy = componente y F Fx Fy De forma que… x

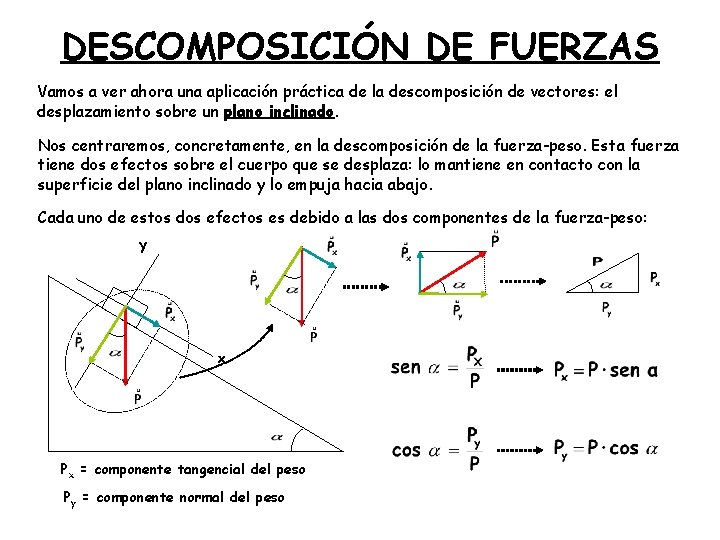
DESCOMPOSICIÓN DE FUERZAS Vamos a ver ahora una aplicación práctica de la descomposición de vectores: el desplazamiento sobre un plano inclinado. Nos centraremos, concretamente, en la descomposición de la fuerza-peso. Esta fuerza tiene dos efectos sobre el cuerpo que se desplaza: lo mantiene en contacto con la superficie del plano inclinado y lo empuja hacia abajo. Cada uno de estos dos efectos es debido a las dos componentes de la fuerza-peso: y x Px = componente tangencial del peso Py = componente normal del peso

DESCOMPOSICIÓN DE FUERZAS En Matemáticas podemos también identificar vectores, componerlos y descomponerlos usando coordenadas cartesianas: y 5 4 3 2 1 1 2 3 4 5 6 x Para componer dos vectores a partir de sus cordenadas cartesianas: y 5 4 3 2 1 1 2 3 4 5 6 x