FUERZA E INTERACCIN Unidad 13 Contenidos 1 1

FUERZA E INTERACCIÓN Unidad 13

Contenidos (1). 1. - Evolución histórica del concepto de fuerza (concepciones pregalineanas). 2. - Naturaleza de las fuerzas 2. 1. Carácter vectorial de la fuerza. 2. 2. Medida de las fuerzas. 2. 3. Fuerza elástica. Ley de Hooke. 3. - Fuerza resultante. 3. 1. Composición de fuerzas concurrentes. 3. 2. Composición de fuerzas paralelas. 3. 3. Descomposición de fuerzas. Componentes normal y tangencial. 2

3 Contenidos (2). 4. - Momento de una fuerza. 4. 1. Par de fuerzas. 5. - Condiciones generales de equilibrio. 5. 1. Palanca y polea. 6. - Interacción gravitatoria. Ley de gravitación universal. Peso de un cuerpo. Campo gravitatorio. 7. - Interacción eléctrica. Ley de Coulomb. Campo eléctrico.

Evolución histórica del concepto de Fuerza l Aristóteles l Galileo l Newton l Definición actual 4

5 Aristóteles Diferencia entre movimientos: – Naturales (caída libre, rotación de planetas). No precisan, al igual que en reposo, la existencia de fuerzas. – No naturales Precisan de fuerzas (aunque sean uniformes). l Si se lanza un objeto, la fuerza existiría mientras exista movimiento l

Galileo “Las fuerzas son las causantes de los cambios de velocidad”. l Por tanto, en el MRU, en donde v es constante no es preciso la existencia de fuerzas. l En cambio, en el MCU, v sí que varía pues aunque no cambie su módulo sí que cambian la dirección y el sentido constantemente. Por tanto, necesita F. l Igualmente un MRUA o un MCUA precisan la existencia de fuerzas. l 6

7 Newton Además de las fuerzas por contacto “vis impresa” existen las fuerzas que actúan a distancia “vis centrípeta” (incluso en el vacío). l Un ejemplo de estas últimas son las “fuerzas gravitatorias” gravitatorias que gobiernan el movimientos de los planetas. l El peso de los cuerpos es una fuerza gravitatoria en donde uno de los objetos es siempre la Tierra. l

Definición actual de Fuerza. Concepto de Dinámica. l Fuerza “es toda acción capaz de cambiar el el estado de reposo o de movimiento, o de producir en él alguna deformación”. l Dinámica “es la ciencia que estudia el movimiento, pero atendiendo a las causas que los producen, es decir, las fuerzas”. 8

Carácter vectorial de las fuerzas. l La fuerza F es una magnitud vectorial ya que posee además de un valor concreto (módulo) una dirección y un sentido determinados. l Por tanto puede expresarse como: l F = Fx· i + Fy· j + Fz· k 9

10 Medida de las fuerzas. Unidades. La unidad de medida de las fuerzas en el Sistema Internacional es el Newton (N) que es la fuerza aplicada a 1 kg de masa para que adquiera una aceleración de 1 m/s 2. l m N = Kg · —— s 2 l l l Otra unidad de fuerza muy usada es el kilopondio (kp) (normalmente llamado “kilo”). 1 kp = 9, 8 N

11 Fuerza elástica. Al estirar un muelle, la deformación de éste es proporcional a la fuerza aplicada. En esta propiedad se basan los dinamómetros para saber la fuerza que se aplica sobre ellos. l La expresión matemática se conoce como Ley de Hooke: l Felast. = – k · r l “k” se conoce como constante elástica y depende lógicamente del tipo de muelle. Felast. r

12 Fuerza elástica (cont). La fuerza que hay que aplicar para estirar o comprimir el muelle (fuerza deformadora) es igual y de sentido contrario ( k · r ). l Normalmente, sólo es necesario calcular el módulo de dicha fuerza. Como el módulo del vector desplazamiento de un punto situado al final del muelle es la variación de longitud del mismo: l F = k · l = k ·|l –l 0|. l

13 Fuerza elástica (cont). Hay una fuerza límite, a partir de la cual el muelle deja de comportarse como elástico. l Por encima de esta fuerza se encuentra el límite de fractura. l F e d y ke o Ho Le x x 0 (long. inicial del muelle)

Ejemplo: 14 Un muelle de constante elástica de 200 N/m tiene una longitud de 50 cm cuando no se aplica ninguna fuerza. Calcula: a) el alargamiento que sufre al aplicar 50 N; b) la fuerza que debe aplicarse para que el muelle mida 60 cm. a) F 50 N l = ————— = 0, 25 m = 25 cm -1 k 200 N·m b) l = 60 cm – 50 cm = 10 cm = 0, 10 m F = k · l = 200 N·m-1 · 0, 10 m = 20 N

15 Suma de fuerzas concurrentes. l l l Sean FA = (4 i + 6 j) N FB = (6 i + 2 j) N La fuerza suma será: FA+B = (10 i + 8 j) N Fy 10 5 FA FA*B FB 5 10 Fx

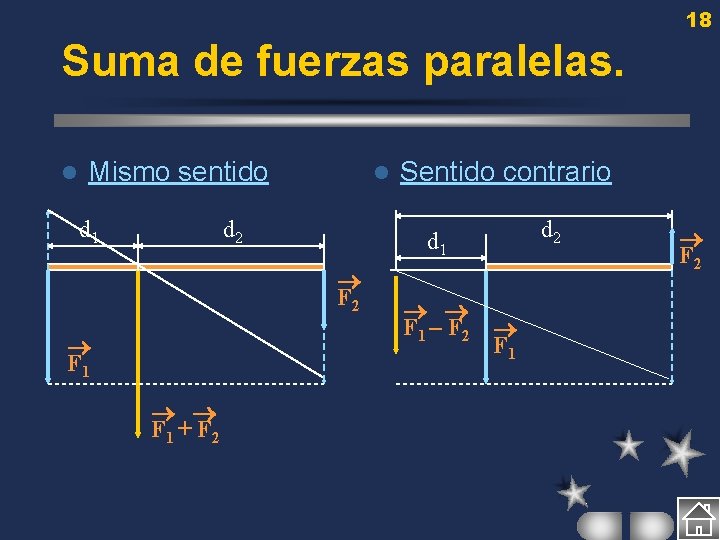
16 Suma de fuerzas paralelas. Al ser las fuerzas vectores deslizantes (se pueden trasladar en la misma dirección) en fuerzas paralelas es imposible hacer el punto de aplicación de ambas fuerzas. l El módulo de la fuerza resultante es la suma (en fuerzas del mismo de la fuerza resultante sentido) o la resta (en fuerzas de sentido contrario) de los módulos de cada fuerza. l

17 Suma de fuerzas paralelas. El Punto de aplicación de la fuerza resultante se obtiene aplicando la ley de la palanca: F 1· d 1 = F 2· d 2, siendo d 1 y d 2 las distancias de las rectas que contienen las fuerzas al Punto de Aplicación de la fuerza resultante. l El Punto de aplicación queda entre medias de las dos rectas paralelas en caso de fuerza del mismo sentido o a un lado (el de la fuerza de mayor módulo) en caso de fuerzas de sentido contrario. l

18 Suma de fuerzas paralelas. l Mismo sentido d 1 l d 2 d 1 F 2 F 1 + F 2 Sentido contrario F 1 – F 2 F 1 d 2 F 2

Ejemplo: En los extremos de una barra de 2 m de 19 longitud se ejercen dos fuerzas paralelas y de sentido contrario de 10 N y 20 N y perpendiculares a la barra. Determina a) el módulo de la fuerza resultante; b) la distancia del punto de aplicación a fuerza de 10 N. Sean F 1 = 10 N y F 2 = 20 N a) R = F 2 – F 1 = 20 N – 10 N = 10 N b) F 1· d 1 = F 2· d 2 Sustituyendo: 10 N · d 1 = 20 N· (d 1 – 2 m) 10 N · d 1 = 20 N · d 1 – 40 N·m 10 N · d 1 = 40 N·m De donde: 40 N·m d 1 = ———— = 4, 0 m 10 N

20 Descomposición de fuerzas Normalmente, las fuerzas oblicuas a la línea de movimiento se descomponen en una fuerza paralela al u. T movimiento PT = PT · u. T PT u. N (PT es la componente PN tangencial) y otra perpendicular al mismo P PN = P N · u. N (PN es la componente normal) l Por ejemplo, el peso cuando actúa en un plano inclinado. l

21 Cálculo de componentes P = PT + PN = P T · u. T + P N · u. N l El ángulo que forman P y PN es el mismo de la inclinación de la rampa (ambos lados perpendiculares). l Por trigonometría se sabe que: PT P PT = P · sen N PN = P · cos l P

Ejemplo: 22 Calcula el valor de las componentes tangencial y normal del peso correspondiente a un cuerpo de 5 kg colocado sobre un plano inclinado de 30º de inclinación. sen 30º = 0, 5; cos 30º = 0, 866 PT = P · sen = m · g · sen ; PN = P · cos = m · g · cos Sustituyendo los datos: PT = 5 kg · 9, 8 m · s– 2 · 0, 5 = 24, 5 N PN = 5 kg · 9, 8 m · s– 2 · 0, 866 = 42, 4 N PT = 24, 5 N PN = 42, 4 N

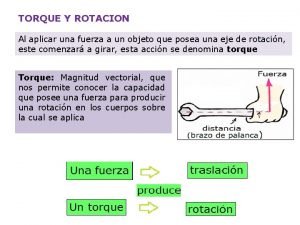
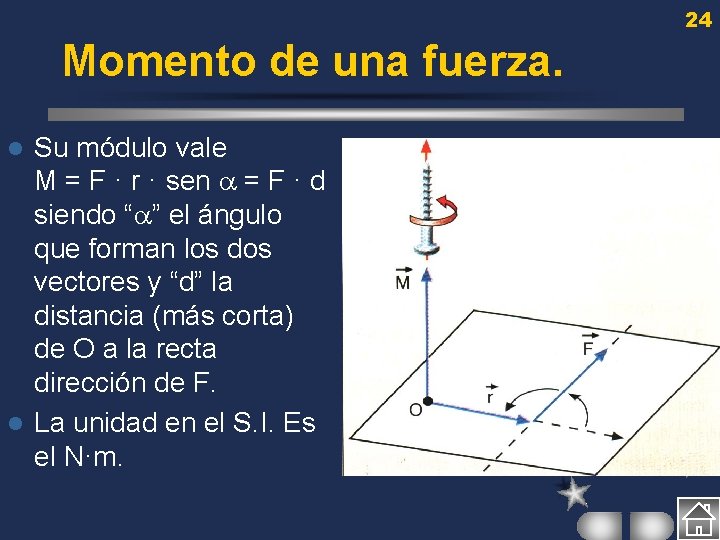
23 Momento de una fuerza. Las fuerzas aplicadas en una dirección que no pasa por el centro de gravedad de un objeto producen un giro en éste. l Para medir la magnitud de este giro se define Momento de una fuerza con respecto a un punto O como un vector cuya dirección es perpendicular al plano que forman O con la recta dirección de F y el sentido lo marca la regla del tornillo. l | M | = | F | · | r | · sen l

24 Momento de una fuerza. Su módulo vale M = F · r · sen = F · d siendo “ ” el ángulo que forman los dos vectores y “d” la distancia (más corta) de O a la recta dirección de F. l La unidad en el S. I. Es el N·m. l

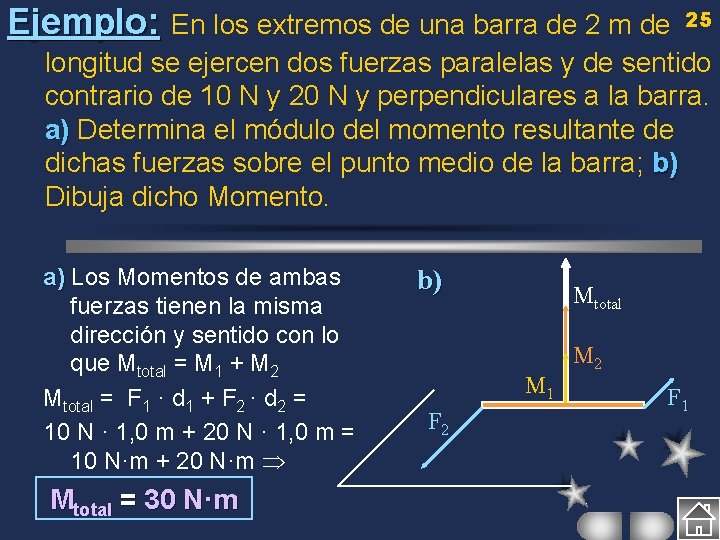
Ejemplo: En los extremos de una barra de 2 m de 25 longitud se ejercen dos fuerzas paralelas y de sentido contrario de 10 N y 20 N y perpendiculares a la barra. a) Determina el módulo del momento resultante de dichas fuerzas sobre el punto medio de la barra; b) Dibuja dicho Momento. a) Los Momentos de ambas fuerzas tienen la misma dirección y sentido con lo que Mtotal = M 1 + M 2 Mtotal = F 1 · d 1 + F 2 · d 2 = 10 N · 1, 0 m + 20 N · 1, 0 m = 10 N·m + 20 N·m Mtotal = 30 N·m b) Mtotal M 1 F 2 M 2 F 1

26 Par de fuerzas. Es un sistema formado por dos fuerzas paralelas de igual módulo pero de sentido contrario aplicadas sobre un sólido rígido. l Al ser fuerzas iguales y de sentido contrario la fuerza resultante es nula con lo que no se produce traslación. l Sin embargo, se produce un giro sobre el punto medio de los P. A. de dichas fuerzas debido a que los Momentos de las mismas tienen el mismo sentido y sus módulos se suman. l

27 Par de fuerzas. l l d d M=F·— +F·—=F·d 2 2 en donde “d” es la distancia que separa las rectas dirección de ambas fuerzas (brazo del par).

Condiciones generales de equilibrio. 28 Se llama “ESTÁTICA” ESTÁTICA a la parte de la Dinámica que estudia los cuerpos en equilibrio (reposo o velocidad constante). l Para que un cuerpo esté en equilibrio deben cumplirse dos condiciones simultaneamente: l l l Fi = 0 No aceleración lineal. (traslación) Mi = 0 No aceleración tangencial. (rotación)

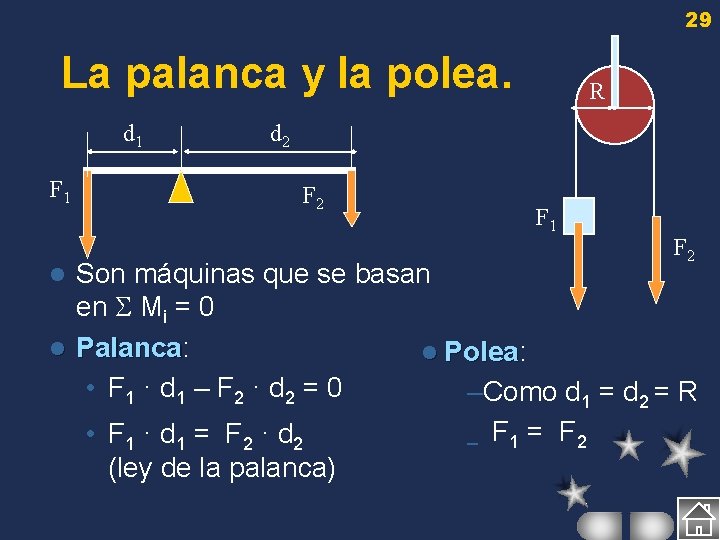
29 La palanca y la polea. d 1 F 1 R d 2 F 1 F 2 Son máquinas que se basan en Mi = 0 l Palanca: Palanca l Polea: Polea • F 1 · d 1 – F 2 · d 2 = 0 –Como d 1 = d 2 = R l • F 1 · d 1 = F 2 · d 2 (ley de la palanca) – F 1 = F 2

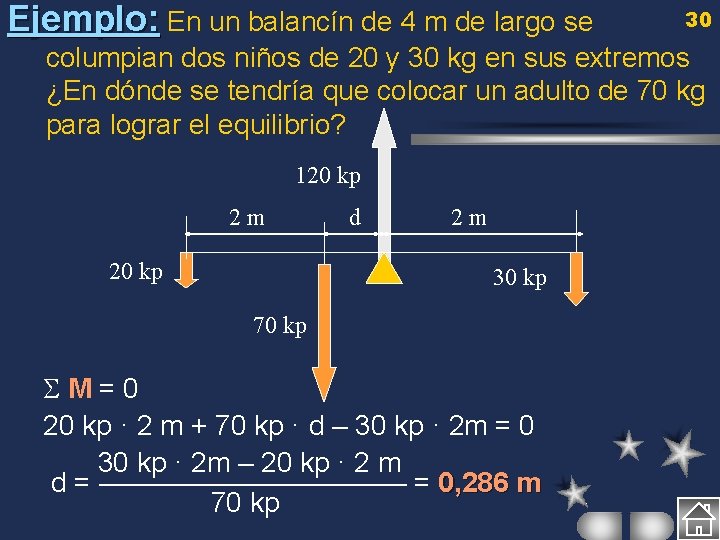
Ejemplo: En un balancín de 4 m de largo se 30 columpian dos niños de 20 y 30 kg en sus extremos ¿En dónde se tendría que colocar un adulto de 70 kg para lograr el equilibrio? 120 kp 2 m 20 kp d 2 m 30 kp 70 kp M=0 20 kp · 2 m + 70 kp · d – 30 kp · 2 m = 0 30 kp · 2 m – 20 kp · 2 m d = —————— = 0, 286 m 70 kp

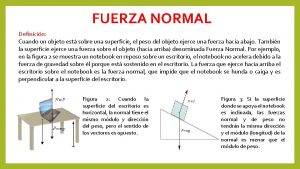
31 Tensión. Siempre que hay objetos suspendidos o unidos por cuerdas, éstas ejercen o transmiten sobre un cuerpo una fuerza debido a la acción del otro cuerpo al que están unidas. l Esta fuerza se denomina “Tensión”. Tensión l Así, por ejemplo, si un cuerpo está suspendido de una cuerda ésta ejerce sobre el cuerpo una fuerza igual al peso y de sentido contrario de forma que la suma de ambas fuerzas sea nula. l T P

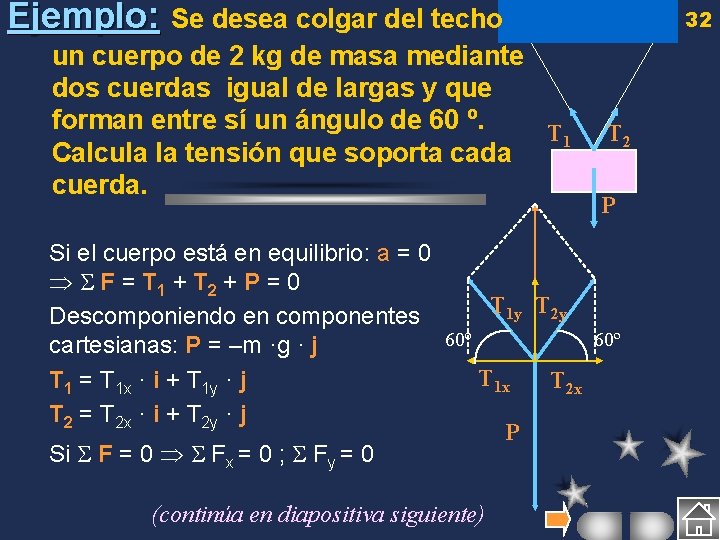
Ejemplo: Se desea colgar del techo un cuerpo de 2 kg de masa mediante dos cuerdas igual de largas y que forman entre sí un ángulo de 60 º. T 1 Calcula la tensión que soporta cada cuerda. 32 T 2 P Si el cuerpo está en equilibrio: a = 0 F = T 1 + T 2 + P = 0 T 1 y T 2 y Descomponiendo en componentes 60º cartesianas: P = –m ·g · j T 1 x T 2 x T 1 = T 1 x · i + T 1 y · j T 2 = T 2 x · i + T 2 y · j P Si F = 0 Fx = 0 ; Fy = 0 (continúa en diapositiva siguiente)

Ejemplo: Se desea colgar del techo un cuerpo de 2 kg de masa mediante dos cuerdas igual de largas y que forman entre sí un ángulo de 60 º. Calcula la tensión que soporta cada cuerda. 33 T 1 T 2 P Las componentes cartesianas se obtienen a partir de T y del ángulo : T 1 x = T 1 · cos 120º = –T 1/2 T 1 y T 2 y – 60º T 1 y = T 1 · sen 120º = 3/2 T 1 60º T 2 x = T 2 · cos 60º = T 2/2 T 1 x T 2 x – T 2 y = T 2 · sen 60º = 3/2 T 2 P Fx = T 1 x + T 2 x = –T 1/2 + T 2/2 = 0 T 1 = T 2 – Fy = T 1 y + T 2 y + P = 3 T 1 – 19, 6 N = 0 T 1 = T 2 = 11, 3 N (viene de diapositiva anterior)

34 Fuerzas naturales l l l Gravitatorias. Eléctricas Magnéticas. Fuerza nucleares fuertes. Fuerza nucleares débiles.

Fuerza gravitatoria 35 Es la fuerza que mantiene unidos los astros responsable del movimiento de los mismos. l Ley de gravitación universal (Newton): m 1 · m 2 m 1 F 12 = – G · ———— u 1 m 2 d 2 F 21 u 1 F 12 2 N· m – 11 G = 6’ 67 · 10 ——— u 2 kg 2 l Normalmente, una vez determinado d la dirección y sentido nos limitamos a calcular el módulo cuya expresión es: m 1 · m 2 F = G · ———— d 2 l

Ejemplo: ¿Cuanto pesará una persona de 75 kg 36 en la Luna sabiendo que la masa de ésta es 7, 35 · 1022 kg y su radio de 1738 km? ¿y en Júpiter? (m. Jupiter = 2 · 1027 kg; r. Jupiter = 7 · 107 m) 2 75 kg · 7, 35· 1022 kg m · m. L N m – 11 —— · ————— = PL = G · ——— = 6’ 67· 10 RLuna 2 kg 2 (1, 738· 106 m)2 PL = 121, 7 N 2 75 kg · 2 · 1027 kg m · mj N m PJ = G · ——— 2= 6’ 67 · 10– 11 —— · ———— = 2 7 2 RJúpiter kg (7· 10 m) PJ = 2042 N

Ejercicio: Sabiendo que la masa del sol es 37 1, 99 · 1030 kg y la fuerza con que atrae a la Tierra es de 3, 54 · 1022 N, calcular la distancia del Sol a la Tierra? (m. Tierra = 5, 97· 1024 kg) d 2 m. T · m. S = G · ——— F 2 5, 97 1024 kg · 1, 99 · 1030 kg N m · d 2 = 6’ 67· 10– 11 —— · ——————— kg 2 3, 54 · 1022 N d = 1, 50 · 1011 m

38 Peso (P) “Es la fuerza con la que la Tierra atrae a los objetos que están en su proximidad”. l Si los cuerpos están cerca de la superficie terrestre, la aceleración que sufren dichos cuerpos es más o menos constante y se denomina “gravedad” l l l P = m · g = m · (– 9, 8 m/s 2 ) · j La componente cartesiana del peso es siempre negativa, pues la masa sólo puede ser positiva, lo que indica que está dirigida siempre hacia abajo.

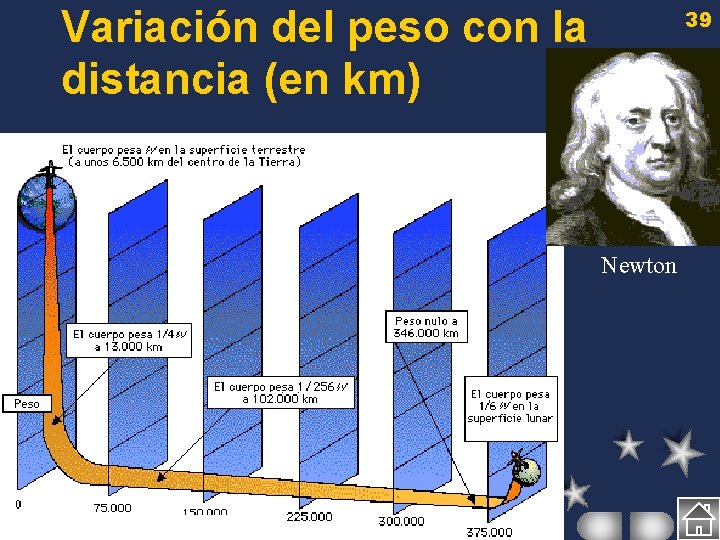
Variación del peso con la distancia (en km) 39 Newton

Gravedad. 40 Newton es el primero en darse cuenta que la fuerza que atrae a dos astros haciendo giran uno con respecto a otro es la misma que provoca la caída de los cuerpos (peso). Igualando ambas fuerzas para un objeto situado en la superficie terrestre: l m · m. Tierra Gravitación F = –G · ————— · u = – m · g· u = m · g (Encarta) 2 RTierra l siendo u un vector unitario perpendicular a la superficie terrestre hacia el exterior. 2 5’ 97 1024 kg l m. Tierra N m · g = G · ——— 2 = 6’ 67 · 10– 11 —— 2 · —————— RTierra kg (6’ 38· 106 m)2 l g = 9’ 8 m/s 2 l

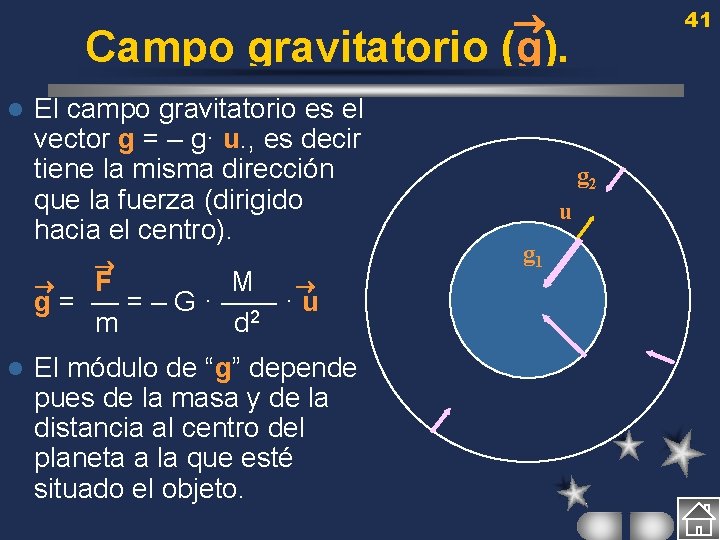
41 Campo gravitatorio (g). l El campo gravitatorio es el vector g = – g· u. , es decir tiene la misma dirección que la fuerza (dirigido hacia el centro). F M g = — = – G · —— ·u 2 m d l El módulo de “g” depende pues de la masa y de la distancia al centro del planeta a la que esté situado el objeto. g 2 u g 1

Ejemplo: ¿Cuanto valdrá el módulo del campo 42 gravitatorio (gravedad) en la órbita geoestacionaria situada a 36200 km de altura? (m. T = 5, 97 · 1024 kg; r. T = 6, 38 · 106 m; G = 6, 67 · 10– 11 N·m 2/kg 2). m. T g = G · ———— 2 2 d (RT + h) 2 24 k g N m 5, 97 10 · g = 6, 67 · 10– 11 —— · ——————— kg 2 (6, 38 · 106 m + 3, 62 · 107 m)2 g = 0, 22 m/s 2

nave espacial de 80 toneladas y módulo del campo gravitatorio en un punto situado a 1/4 parte de la 43 distancia que une la Tierra y la Luna desde la Luna y en el segmento entre ambos astros. Haz un esquema de la fuerza y del campo. (G = 6, 67 · 10– 11 N·m 2·kg– 2. Distancia Tierra-Luna: d = 3, 84· 108 m; MT = 5, 98 · 1024 kg; ML = 7, 47 · 1022 kg) g. T g. L Luna Tierra g 2 5’ 98 1024 kg MT N m · 2 g. T = G · — 2 = 6’ 67 · 10– 11 —— · —————— =0, 00481 m/s d kg 2 (2, 88· 108 m)2 2 7, 47· 1022 kg ML N m 2 g. L = G · — 2 = 6’ 67 · 10– 11 —— · —————— =0, 00054 m/s d kg 2 (9, 6· 107 m)2 g = g. T – g. L = 0, 00481 m/s 2 – 0, 00054 m/s 2 = 0, 00427 m/s 2 F = m · g = 80000 kg · 0, 00427 m/s 2 = 341, 6 N

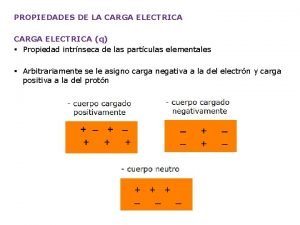
Carga eléctrica. l l l Es una propiedad de la materia. Puede ser positiva o negativa según el cuerpo tenga defecto o exceso de electrones. Puede trasmitirse de unos cuerpos a otros bien por contacto, o incluso, a distancia, al producirse descargas (rayos). Son los electrones las partículas que pasan de unos cuerpos a otros. Se mide en culombios. (C). La carga de un electrón es – 1’ 6 · 10– 19 C. 44

Ley de Coulomb. Cargas del mismo signo se repelen entre sí. l Cargas de distinto signo se atraen entre sí. l La fuerza con que se atraen o repelen dos cargas vienen determinada por la ley de Coulomb: l q 1 · q 2 N · m 2 9 ——— F 12 = – F 21 = K ·——— · u ; K = 9 · 10 12 d 2 C 2 l en donde K depende del medio y u 12 es un vector unitario cuya dirección es la línea que une las cargas q 1 y q 2 y el sentido va de 1 hacia 2. 45

46 Ley de Coulomb (cont. ) Normalmente, una vez determinado la dirección y sentido nos limitamos a calcular el módulo cuya expresión: (no es preciso poner signo a las cargas) 2 l q 1 · q 2 N · m 9 ——— F = K · ——— ; K = 9 · 10 d 2 C 2 l Si existen dos cargas que actúan sobre una tercera, habrá que sumar las fuerzas que cada una ejerce sobre la tercera de manera vectorial. l Las fuerzas eléctricas tienen valores muy superiores a las gravitatorias y unen el “microcosmos” l

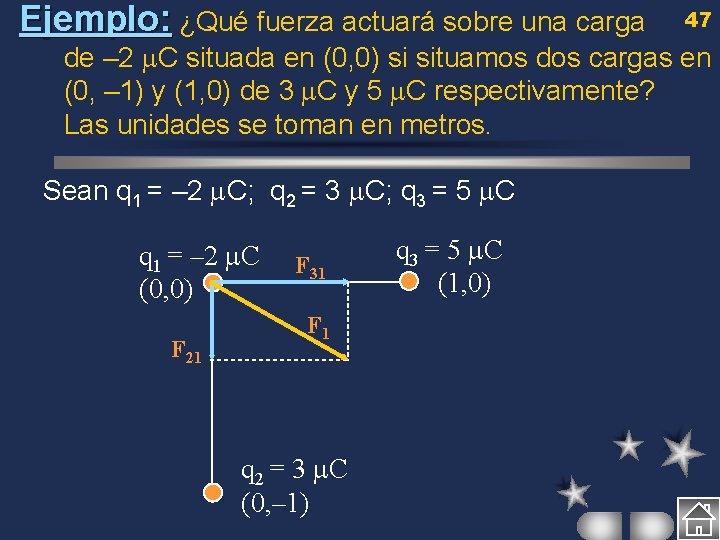
Ejemplo: ¿Qué fuerza actuará sobre una carga 47 de – 2 C situada en (0, 0) si situamos dos cargas en (0, – 1) y (1, 0) de 3 C y 5 C respectivamente? Las unidades se toman en metros. Sean q 1 = – 2 C; q 2 = 3 C; q 3 = 5 C q 1 = – 2 C (0, 0) F 21 F 31 F 1 q 2 = 3 C (0, – 1) q 3 = 5 C (1, 0)

Ejemplo: ¿Qué fuerza actuará sobre una carga 48 de – 2 C situada en (0, 0) si situamos dos cargas en (0, – 1) y (1, 0) de 3 C y 5 C respectivamente? Las unidades se toman en metros. Sean q 1 = – 2 C; q 2 = 3 C; q 3 = 5 C 2 – 2· 10– 6 C · 3· 10– 6 C q 1 · q 2 N · m 9 ——— · ————— ·j F 21 = K · ——— ·j = 9 · 10 d 2 C 2 1 m 2 2 – 6 C · 5· 10– 6 C q 1 · q 3 N ·m – 2· 10 9 ——— · ————— ·(–i) F 31 = K·——— ·(–i) = 9· 10 d 2 C 2 1 m 2 F 21 = – 0, 054 N j ; F 31 = 0, 090 N i ; F 1 = (0, 090 i – 0, 054 j) N F 1 = (F 212 + F 312)½ = [(– 0, 054 N)2 + (0, 090 N)2]½ = F 1 = 0, 105 N = arctg [0, 090/(– 0, 054)] = –(59º 2’ 10”)

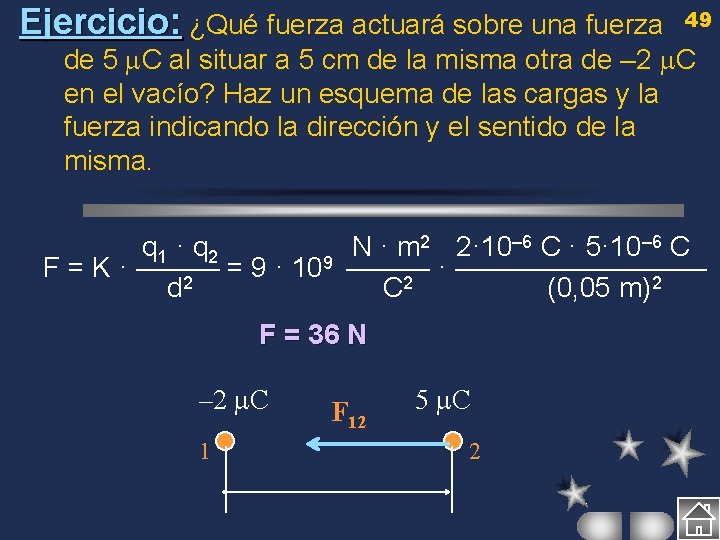
Ejercicio: ¿Qué fuerza actuará sobre una fuerza 49 de 5 C al situar a 5 cm de la misma otra de – 2 C en el vacío? Haz un esquema de las cargas y la fuerza indicando la dirección y el sentido de la misma. 2 2· 10– 6 C · 5· 10– 6 C q 1 · q 2 N · m 9 ——— · ————— F = K · ——— = 9 · 10 d 2 C 2 (0, 05 m)2 F = 36 N – 2 C 1 F 12 5 C 2

Ejercicio: ¿A qué distancia en el vacío estarán colocadas dos cargas de 3 C y 6 C para que se repelar con una fuerza cuyo módulo es de 3 N? d 2 q 1 · q 2 = K · ——— F 2 3· 10– 6 C · 6 · 10– 6 C N m 2 d 2 = 9· 109 —— · ————— = 0, 054 m C 2 3 N Realizando la raiz cuadrada se tiene: d = 0, 23 m 50

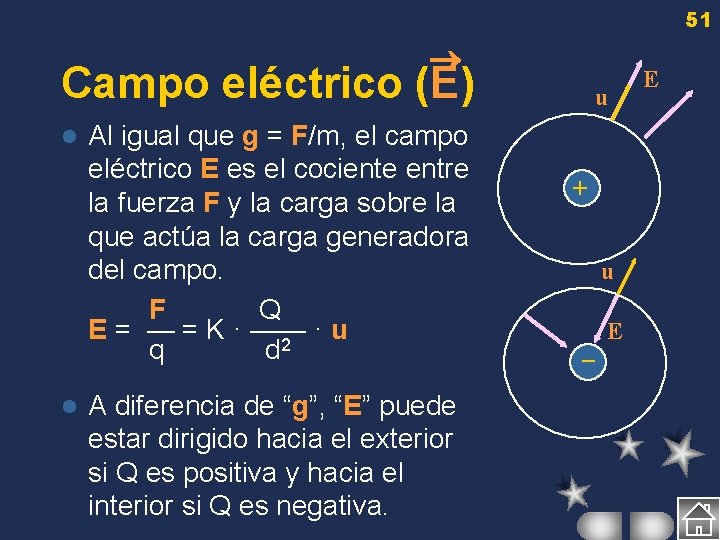
51 Campo eléctrico (E) l l Al igual que g = F/m, el campo eléctrico E es el cociente entre la fuerza F y la carga sobre la que actúa la carga generadora del campo. F Q E = — = K · —— ·u 2 q d A diferencia de “g”, “E” puede estar dirigido hacia el exterior si Q es positiva y hacia el interior si Q es negativa. u + u E – E

Ejemplo: Dos 52 cargas eléctricas de +10 C y – 30 C están situadas en (0, 0) y (3, 0) respectivamente. Calcula el valor del campo eléctrico en (1, 0). Las unidades se toman en metros. q 1 = +10 C (0, 0) u 1 q 2 = – 30 C (3, 0) E 2 (1, 0) E 1 E u 2 q 1 q 2 E = E 1 + E 2 = K · ——· u 1+ K · —— u 2 2 2 d 1 d 2 2 10 · 10– 6 C N · m – 30 · 10 9 E = 9 · 10 ————— u + ————— (–u ) 1 1 C 2 (1 m)2 (2 m)2 E = 157500 N · C– 1 u 1

Otras fuerzas naturales l 53 Fuerza magnética: – Se produce entre imanes o cargas en movimiento. – Va unida a la eléctrica por lo que hablamos de fuerza “electromagnética”. l Fuerza nuclear fuerte: – Son las más intensas de todas. – Son las responsables de la unión de nucleones (protones y neutrones) en el núcleo. – Tienen un alcance del orden de 10– 15 m. l Fuerza nuclear débil: – Son las responsable de la desintegración radiactiva. – Tienen un alcance del orden de 10– 17 m.