Universidade Federal do Rio de Janeiro COPPE Programa

Universidade Federal do Rio de Janeiro COPPE – Programa de Engenharia Química OTIMIZAÇÃO DE PROCESSOS Prof. Argimiro R. Secchi AULA 5: - Programação Inteira Mista e Multi-objetivo 2019 1

Programação Inteira Mista (MIP) min S(x, y) sujeito a: hj(x, y) = 0 , j = 1, 2, . . . , m gj(x, y) 0 , j = 1, 2, . . . , p x X n e y Y q Frequentemente as variáveis inteiras y Y = {0, 1}q binárias, seja por definição ou por conversão de base: z Z e zl z zu pode ser descrita por y Y = {0, 1}q z = zl + y 1 + 2 y 2 + 4 y 3 +. . . + 2 q-1 yq 2

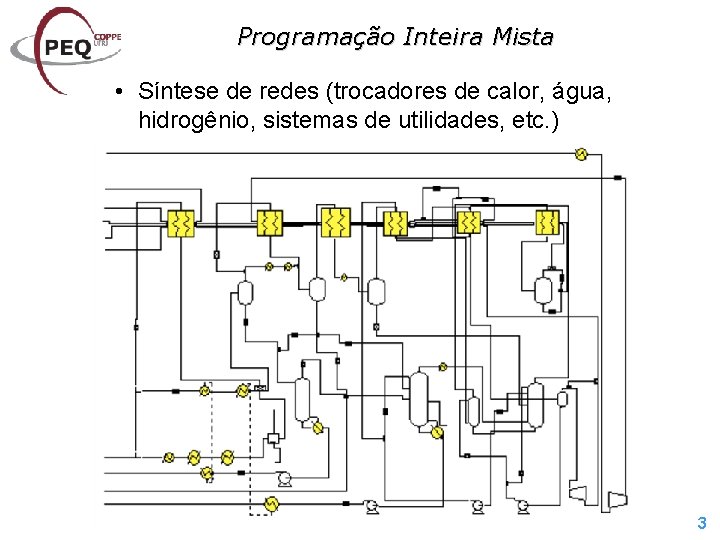
Programação Inteira Mista • Síntese de redes (trocadores de calor, água, hidrogênio, sistemas de utilidades, etc. ) 3

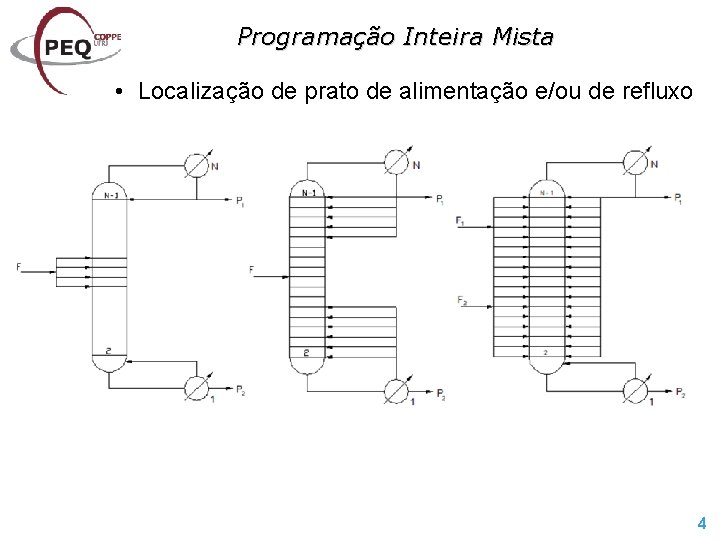
Programação Inteira Mista • Localização de prato de alimentação e/ou de refluxo 4

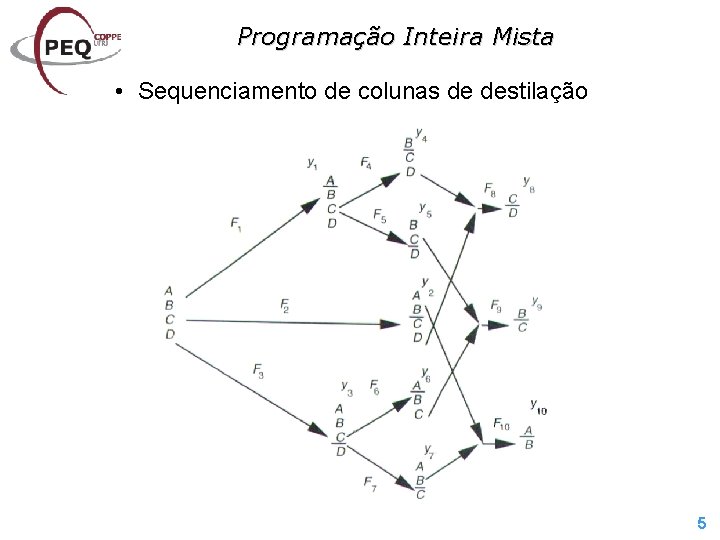
Programação Inteira Mista • Sequenciamento de colunas de destilação 5

Programação Inteira Mista • Síntese de processos com superestruturas Exemplo: hidrodealquilação do tolueno 6

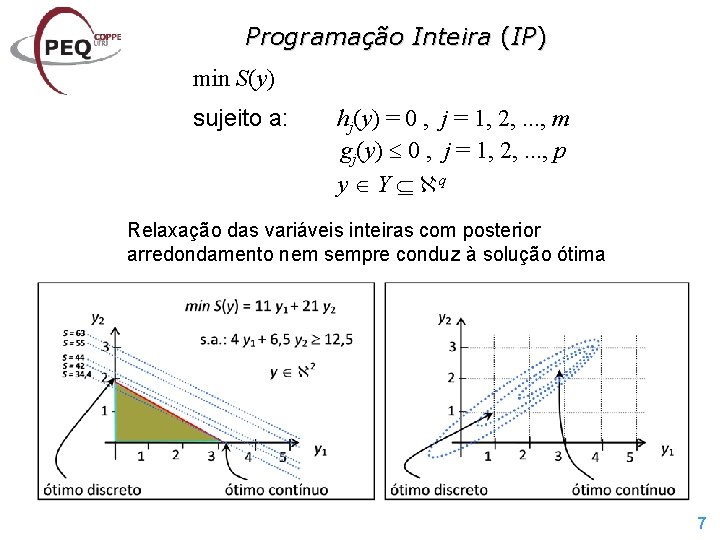
Programação Inteira (IP) min S(y) sujeito a: hj(y) = 0 , j = 1, 2, . . . , m gj(y) 0 , j = 1, 2, . . . , p y Y q Relaxação das variáveis inteiras com posterior arredondamento nem sempre conduz à solução ótima 7

Programação Inteira Binária (BIP) min S(y) sujeito a: hj(y) = 0 , j = 1, 2, . . . , m gj(y) 0 , j = 1, 2, . . . , p y Y = {0, 1}q Problema da mochila: colocar até q artigos (yi) valiosos, com peso (ou volume) wi e valor ci, dentro de uma mochila, não ultrapassando o peso (ou volume) máximo W, de modo a maximizar o valor total dos artigos. max S(y) = c. T y sujeito a: w. T y W , y Y = {0, 1}q Problema do caixeiro viajante: vendedor visita n cidades somente uma vez, retornando para a cidade de origem, percorrendo o menor caminho possível. max (cij: distância entre as cidades i e j) sujeito a: , , yii = 0, i, j = 1, 2, . . . , n y Y = {0, 1}q=n n 8

Programação Linear Inteira Mista (MILP) min S(x, y) = c. T x + d. T y P Ax+By b x 0 x X n e y Y = {0, 1}q sujeito a: Solução por enumeração (busca exaustiva): 2 q LPs y Y = {0, 1}3 y 1 0 0 1 1 0 1 y 2 0 0 1 0 1 1 y 3 0 0 0 1 1 1 9

Programação Linear Inteira Mista (MILP) Método dos Planos de Cortes 1) Resolve-se o MILP com as variáveis inteiras relaxadas LP. Se a solução do LP possuir todas as variáveis relaxadas inteiras, então a solução ótima do problema original foi encontrada; 2) Caso contrário, elimina-se a solução obtida pela adição de restrições extras ao problema (planos de corte), sem eliminar qualquer solução inteira, ir para (1). Exemplo 5. 1: min S(y) = 10 y 1 11 y 2 sujeito a: 10 y 1 + 12 y 2 59 y 0, y Y 2 MILP relaxado (LP): y = [5, 9 0]T 10

Programação Linear Inteira Mista (MILP) Método dos Planos de Cortes Plano de corte: y 1 5 LP: y = [5 0, 75]T Plano de corte: y 1 + y 2 5 LP: y = [0, 5 4, 5]T Planos de cortes: y 1 + y 2 5 y 2 4 LP: y = [1 4]T (solução ótima) 11

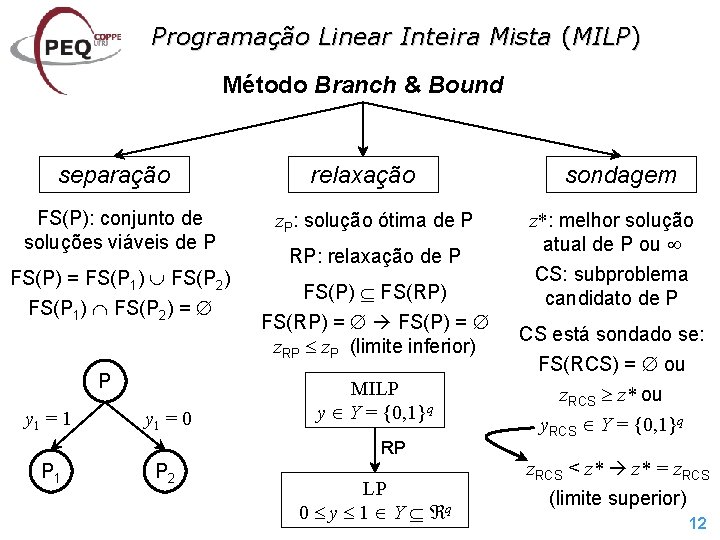
Programação Linear Inteira Mista (MILP) Método Branch & Bound separação FS(P): conjunto de soluções viáveis de P FS(P) = FS(P 1) FS(P 2) = P y 1 = 1 y 1 = 0 relaxação z. P: solução ótima de P RP: relaxação de P FS(P) FS(RP) = FS(P) = z. RP z. P (limite inferior) MILP y Y = {0, 1}q RP P 1 P 2 LP 0 y 1 Y q sondagem z*: melhor solução atual de P ou CS: subproblema candidato de P CS está sondado se: FS(RCS) = ou z. RCS z* ou y. RCS Y = {0, 1}q z. RCS < z* = z. RCS (limite superior) 12

Programação Linear Inteira Mista (MILP) Método Branch & Bound 1) Inicializar a lista de subproblemas (CS) = (P), ou árvore binária, z* = ; 2) Se a lista de subproblemas (CS) estiver vazia, então FIM (se z* = , então não existe solução viável); 3) Selecionar um candidato da lista, tornando-o candidato (CS) corrente; 4) Selecionar e resolver a relaxação (RCS) do (CS) corrente, obtendo a solução z. RCS; 5) Aplicar os três critérios de sondagem: (i) Se (RCS) é inviável, então o (CS) corrente não tem solução viável e (ir para 2); (ii) Se z. RCS z*, então o (CS) corrente não tem solução viável melhor que z* e (ir para 2); (iii) Se a solução ótima de (RCS) é viável para (CS) e z. RCS < z*, então z* z. RCS (limite superior) e (ir para 2); 6) Separar o (CS) corrente e adicionar os seus subproblemas filhos na lista de subproblemas (CS) e (ir para 2). 13

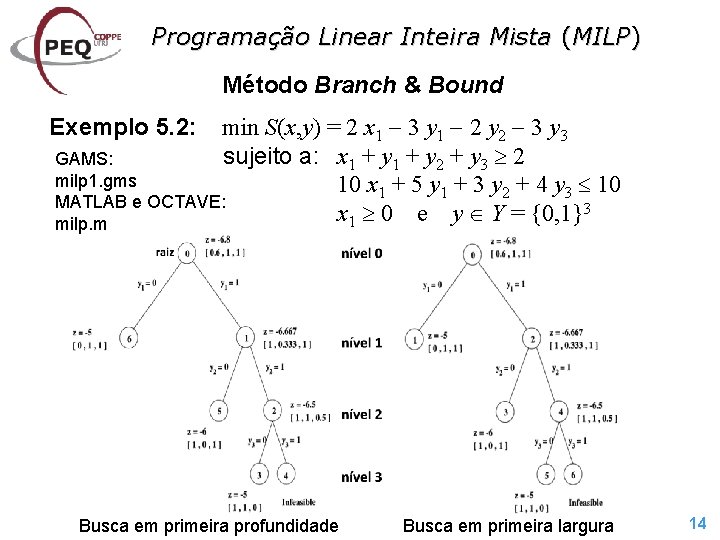
Programação Linear Inteira Mista (MILP) Método Branch & Bound min S(x, y) = 2 x 1 3 y 1 2 y 2 3 y 3 sujeito a: x 1 + y 2 + y 3 2 GAMS: milp 1. gms 10 x 1 + 5 y 1 + 3 y 2 + 4 y 3 10 MATLAB e OCTAVE: 3 x 0 e y Y = {0, 1} 1 milp. m Exemplo 5. 2: Busca em primeira profundidade Busca em primeira largura 14

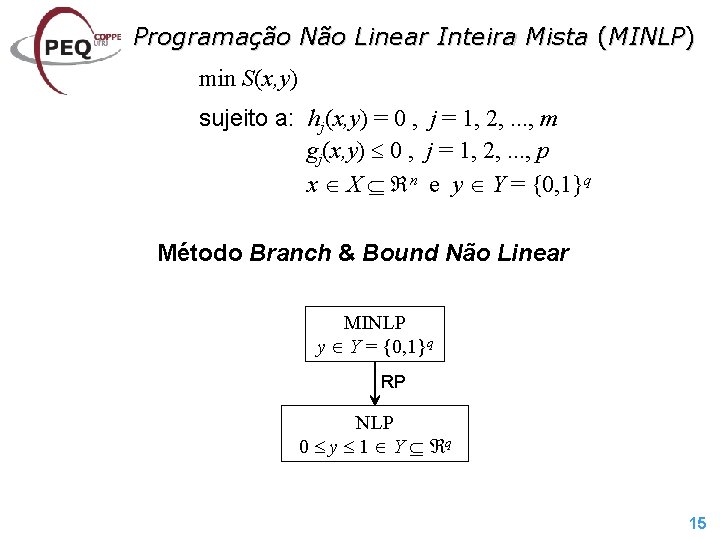
Programação Não Linear Inteira Mista (MINLP) min S(x, y) sujeito a: hj(x, y) = 0 , j = 1, 2, . . . , m gj(x, y) 0 , j = 1, 2, . . . , p x X n e y Y = {0, 1}q Método Branch & Bound Não Linear MINLP y Y = {0, 1}q RP NLP 0 y 1 Y q 15

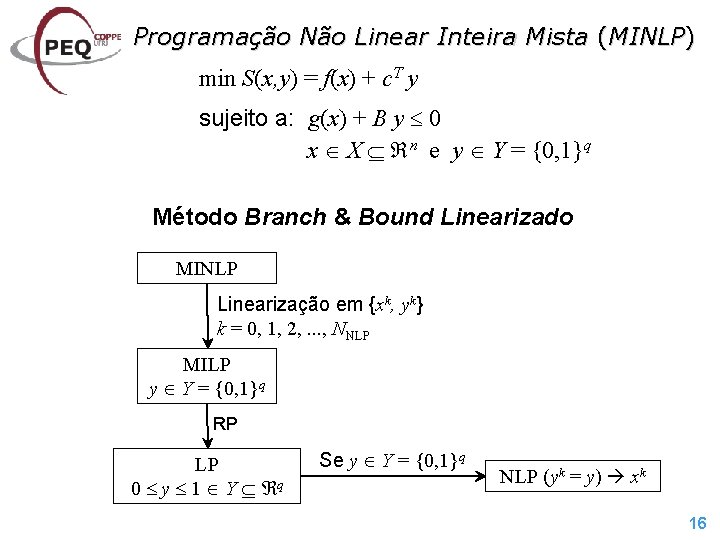
Programação Não Linear Inteira Mista (MINLP) min S(x, y) = f(x) + c. T y sujeito a: g(x) + B y 0 x X n e y Y = {0, 1}q Método Branch & Bound Linearizado MINLP Linearização em {xk, yk} k = 0, 1, 2, . . . , NNLP MILP y Y = {0, 1}q RP LP 0 y 1 Y q Se y Y = {0, 1}q NLP (yk = y) xk 16

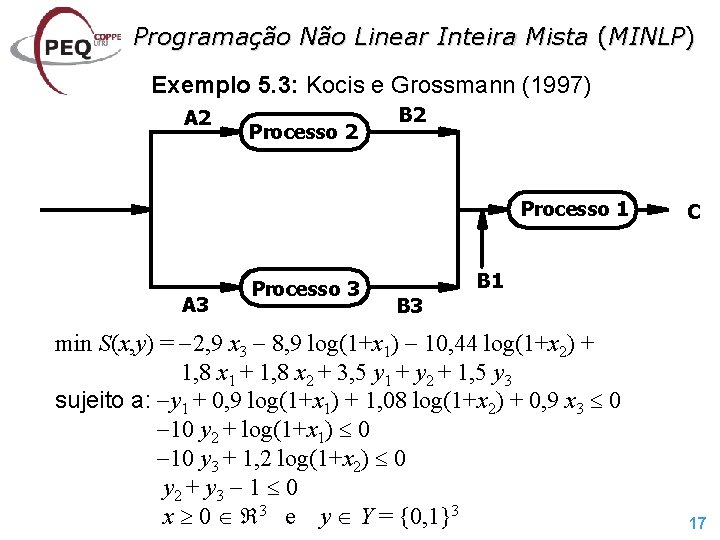
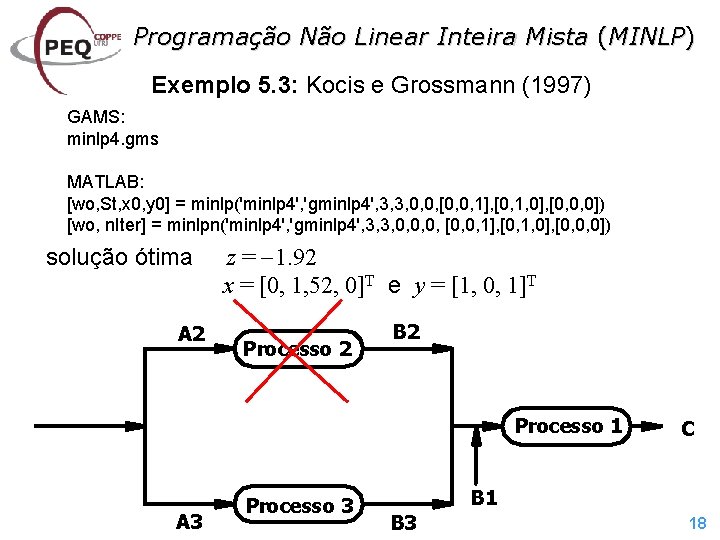
Programação Não Linear Inteira Mista (MINLP) Exemplo 5. 3: Kocis e Grossmann (1997) A 2 Processo 2 B 2 Processo 1 A 3 Processo 3 C B 1 B 3 min S(x, y) = 2, 9 x 3 8, 9 log(1+x 1) 10, 44 log(1+x 2) + 1, 8 x 1 + 1, 8 x 2 + 3, 5 y 1 + y 2 + 1, 5 y 3 sujeito a: y 1 + 0, 9 log(1+x 1) + 1, 08 log(1+x 2) + 0, 9 x 3 0 10 y 2 + log(1+x 1) 0 10 y 3 + 1, 2 log(1+x 2) 0 y 2 + y 3 1 0 x 0 3 e y Y = {0, 1}3 17

Programação Não Linear Inteira Mista (MINLP) Exemplo 5. 3: Kocis e Grossmann (1997) GAMS: minlp 4. gms MATLAB: [wo, St, x 0, y 0] = minlp('minlp 4', 'gminlp 4', 3, 3, 0, 0, [0, 0, 1], [0, 1, 0], [0, 0, 0]) [wo, n. Iter] = minlpn('minlp 4', 'gminlp 4', 3, 3, 0, 0, 0, [0, 0, 1], [0, 1, 0], [0, 0, 0]) solução ótima A 2 z = 1. 92 x = [0, 1, 52, 0]T e y = [1, 0, 1]T Processo 2 B 2 Processo 1 A 3 Processo 3 C B 1 B 3 18

Otimização Multi-objetivo min F(x) = [F 1(x) F 2(x). . . Fq(x)]T sujeito a: hj(x) = 0 , j = 1, 2, . . . , m gj(x) 0 , j = 1, 2, . . . , p x X n = {x X n | h(x) = 0, g(x) 0} = {y = F(x) q | x } 19

Otimização Multi-objetivo Um ponto x* , é uma solução não inferior (pertence ao conjunto de Pareto) se para alguma vizinhança de x* não existe um x tal que (x* + x) e: Fi(x* + x) Fi(x*) , i = 1, 2, . . . , q Fj(x* + x) < Fj(x*) , para algum j 20

Otimização Multi-objetivo Exemplo 5. 4: min F(x) = [F 1(x) F 2(x)]T sujeito a: F 1(x) = 1 + ½ x 2 F 2(x) = 4 (x ½)2 + ½ x 0 21

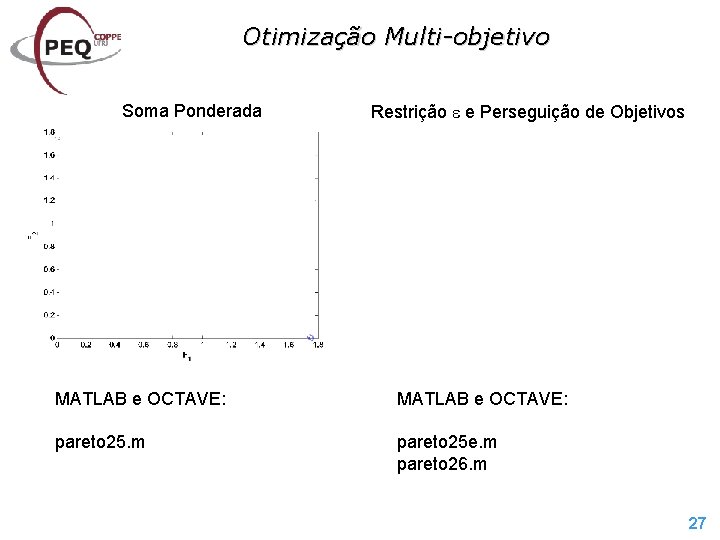
Otimização Multi-objetivo Método da Soma Ponderada min S(x) = w. T F(x) sujeito a: hj(x) = 0 , j = 1, 2, . . . , m gj(x) 0 , j = 1, 2, . . . , p x X n w 0 Para o Exemplo 5. 3: min S(x) = w. T F(x) = w 1 F 1(x) + (1 w 1) F 2(x) sujeito a: x 0 MATLAB e OCTAVE: pareto 19. m Conjunto de Pareto: P = {x*(w 1) | 0 w 1 1} = {0 x ½} 22

Otimização Multi-objetivo Método das Restrições min Fr(x) sujeito a: hj(x) = 0 , j = 1, 2, . . . , m gj(x) 0 , j = 1, 2, . . . , p Fi(x) i , i = 1, 2, . . . , q , i r x X n Para o Exemplo 5. 3: min S(x) = F 2(x) sujeito a: F 1(x) x 0 MATLAB e OCTAVE: pareto 20. m Conjunto de Pareto: P = {x*( ) | 1 1, 125} = {0 x ½} 23

Otimização Multi-objetivo Método da Perseguição dos Objetivos min sujeito a: hj(x) = 0 , j = 1, 2, . . . , m gj(x) 0 , j = 1, 2, . . . , p Fi(x) wi , i = 1, 2, . . . , q x X n e Para o Exemplo 5. 3: min S(x, ) = sujeito a: F 1(x) w 1 1 F 2(x) (1 w 1) ½ x 0 MATLAB e OCTAVE: pareto 18. m Conjunto de Pareto: P = {x*(w 1) | 0 w 1 1} = {0 x ½} 24

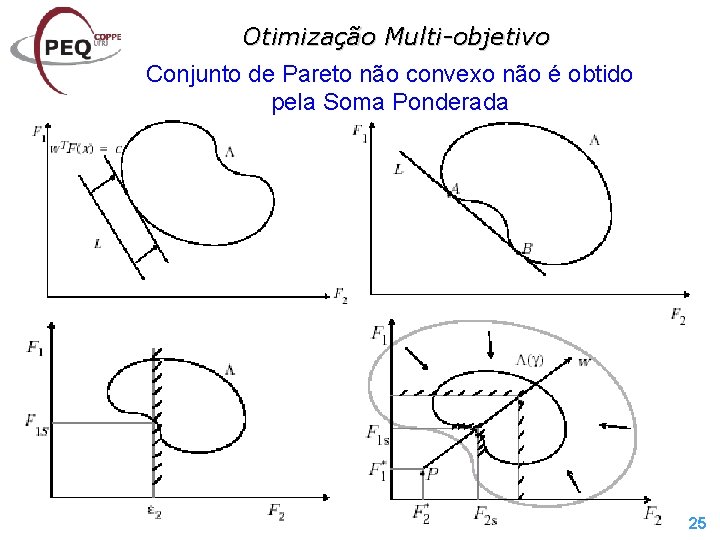
Otimização Multi-objetivo Conjunto de Pareto não convexo não é obtido pela Soma Ponderada 25

Otimização Multi-objetivo Exemplo 5. 5: min F(x) = [F 1(x) F 2(x)]T sujeito a: F 1(x) = atan(x+2)2 F 2(x) = atan(x 2)2 x 26

Otimização Multi-objetivo Soma Ponderada Restrição e Perseguição de Objetivos MATLAB e OCTAVE: pareto 25. m pareto 25 e. m pareto 26. m 27

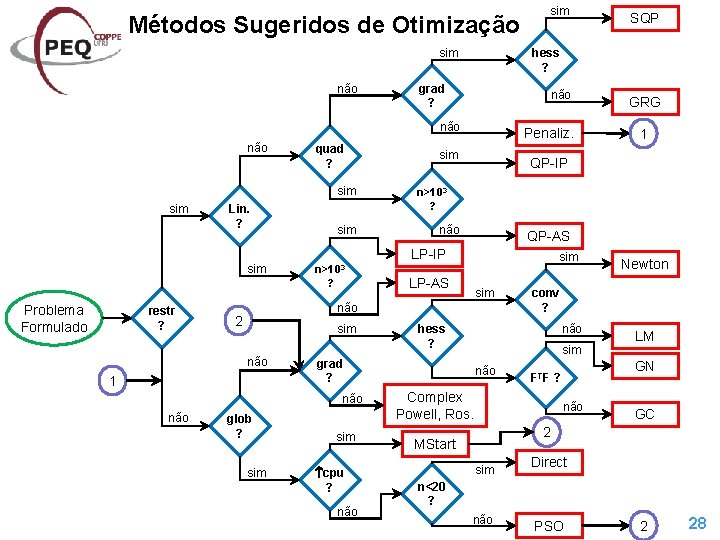
Métodos Sugeridos de Otimização sim não quad ? sim Lin. ? sim grad ? não ? Problema Formulado restr ? sim 2 sim 1 glob ? sim cpu ? não 1 n>103 ? não QP-AS sim LP-AS sim não Newton conv ? hess ? grad ? não GRG QP-IP não não Penaliz. LP-IP n>103 SQP hess ? não sim GN FTF ? Complex Powell, Ros. LM não GC 2 MStart sim Direct n<20 ? não PSO 2 28

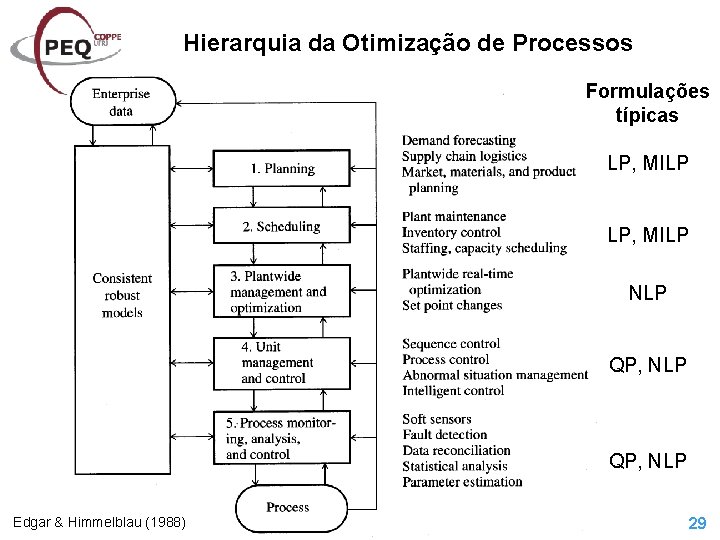
Hierarquia da Otimização de Processos Formulações típicas LP, MILP NLP QP, NLP Edgar & Himmelblau (1988) 29

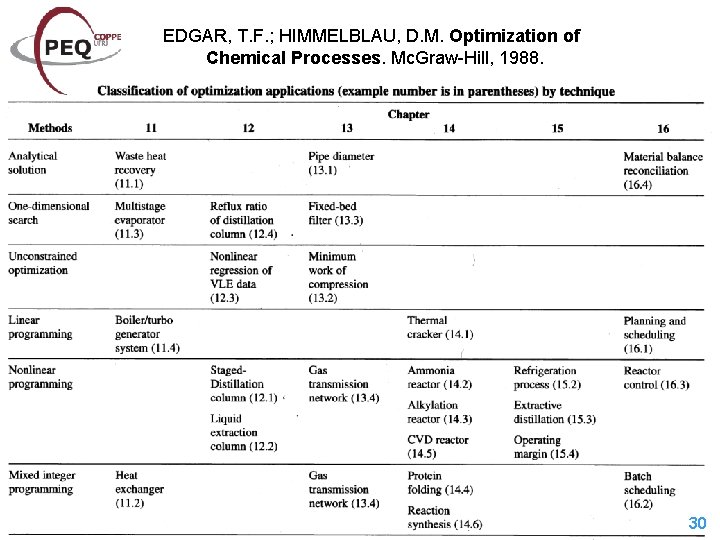
EDGAR, T. F. ; HIMMELBLAU, D. M. Optimization of Chemical Processes. Mc. Graw-Hill, 1988. 30