TRIGONOMETRI C IDENTITIES Identities and Equations equation such

TRIGONOMETRI C IDENTITIES

Identities and Equations equation such as y 2 – 9 y + 20 = (y – 4)(y – 5) is an identity because the left-hand side (LHS) is equal to the right-hand side (RHS) for whatever value is substituted to the variable. � Based on the example, an identity is defined as an equation, which is true for all values in the domain of the variable. � An

Identities and Equations � There are identities which involve trigonometric functions. These identities are called trigonometric identities. � Trigonometric identity is an equation that involves trigonometric functions, which is true for all the values of θ for which the functions are defined.

Identities and Equations �A conditional equation is an equation that is true only for certain values of the variable. � The equations y 2 – 5 y + 6 = 0 and x 2 – x – 6 = 0 are both conditional equations. The first equation is true only if y = 2 and y = 3 and the second equation is true only if x = 3 and x = -2.

The Fundamental Identities

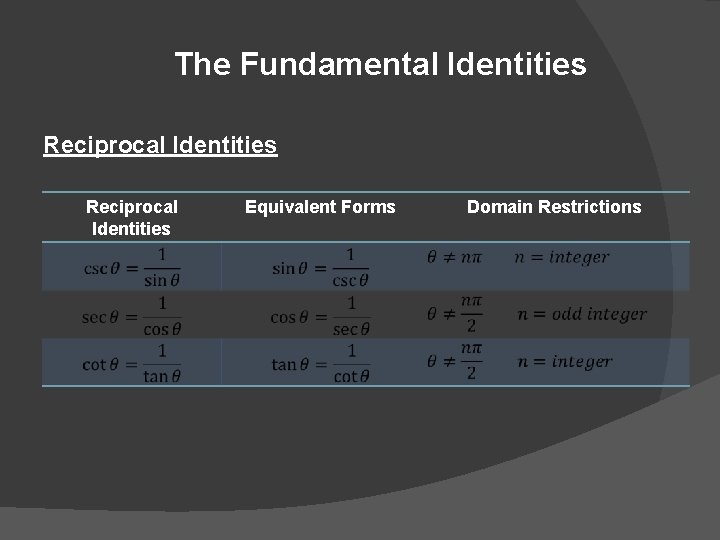
The Fundamental Identities Reciprocal Identities Equivalent Forms Domain Restrictions

Quotient (or Ratio) Identities Quotient Identities Domain Restrictions

Pythagorean Identities Negative Arguments Identities

Notes: � The real number x or θ in these identities may be changed by other angles such as α, β, γ, A, B, C, …. � The resulting identities may then be called trigonometric identities.

Example: �

Simplifying Expressions �

Proving Identities � There is no exact procedure to be followed in proving identities. However, it may be helpful to express all the given functions in terms of sines and cosines and then simplify. � To establish an identity, we may use one of the following: 1. Transform the left member into the exact form of the right. 2. Transform the right into the exact form of the left, or 3. Transform each side separately into the same form.

Examples �

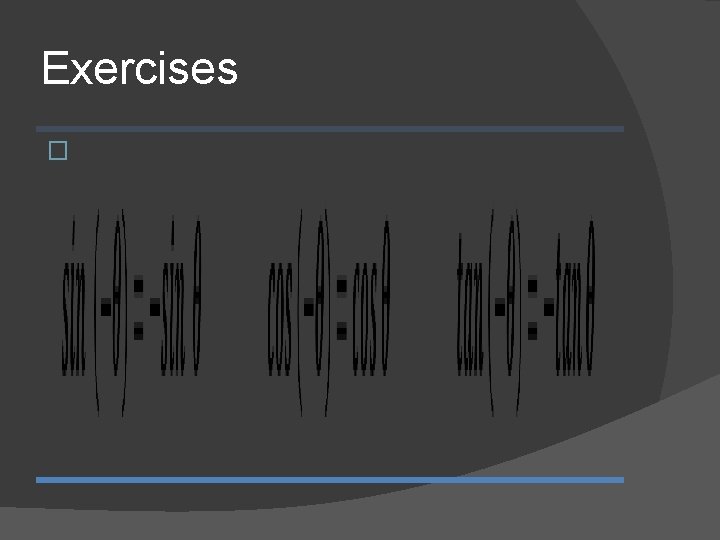
Exercises �

Exercises �

Do Worksheet 6

Sum and Difference Identities

Double-Angle Identities Sine Cosine Tangent

Half-Angle Identities Sine Cosine Tangent

Product-to-Sum and Sum-to-Product Identities Product-to-Sum Identities

Product-to-Sum and Sum-to. Product Identities Sum-to-Product Identities

Examples �