Transformational Geometry Math 314 Game Plan Distortions Orientations

Transformational Geometry Math 314

Game Plan § Distortions § Orientations § Parallel Path § Translation § Rotation § Reflection

Game Plan Con’t § Combination – Glide Reflection § Combinations § Single Isometry § Similtudes Dilutation § Series of Tranformation

Transformation § Any time a figure is moved in the plane we call this a § § transformation. As mathematicians we like to categorize these transformations. The first category we look at are the ugly ones or distortions § Transformation Formula § Format (x, y) (a, b) The old x becomes a old y becomes b

Using a Graph § Let’s try one on graph paper § Consider A (1, 4) B (7, 2) C (3, – 1) § (x, y) (x + y, x – y) § Step 1: Calculate the new points § Step 2: Plot the points i. e A A’ B B’ etc. § A (1, 4) (5, -3) A’ § B (7, 2) (9, 5) B’ § C (3 – 1) (2, 4) C’

Ex#1: Put on Graph Paper B’ Formula Box (x, y) (x+y, x-y) A (1, 4) (5, -3) A’ B (7, 2) (9, 5) B’ C (3, – 1) (2, 4) C’ Notice, this graph is off the page… make sure yours does not A C’ B C A’

Orientation § To examine figures, we need to know how they line up. § We are concerned with Clockwise (CW) Counterclockwise (CCW)

Orientation § Consistency is Key § Start with A go ccw A § Eg A’ B C B’ C’ Orientation ABC and A’ B’ C’ Orientation is the same

Orientation Con’t A B A’ C B’ C’ What happened to the orientation? Orientation has changed

Orientation Vocabulary § Orientation the § Orientation same… or § preserved § unchanged § constant changed or § not preserved § changed § not constant

Parallel Paths § When we move or transform an object, we are interested in the path the object takes. To look at that we focus on paths taken by the vertices

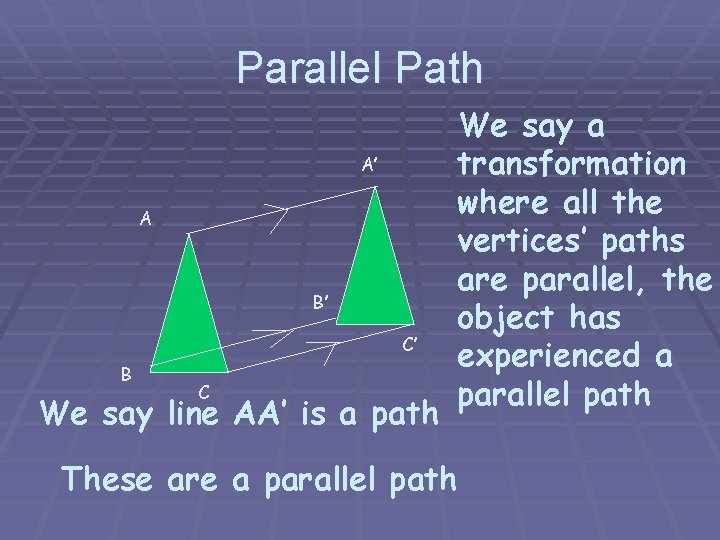
Parallel Path A’ A B’ C’ B C We say line AA’ is a path We say a transformation where all the vertices’ paths are parallel, the object has experienced a parallel path These are a parallel path

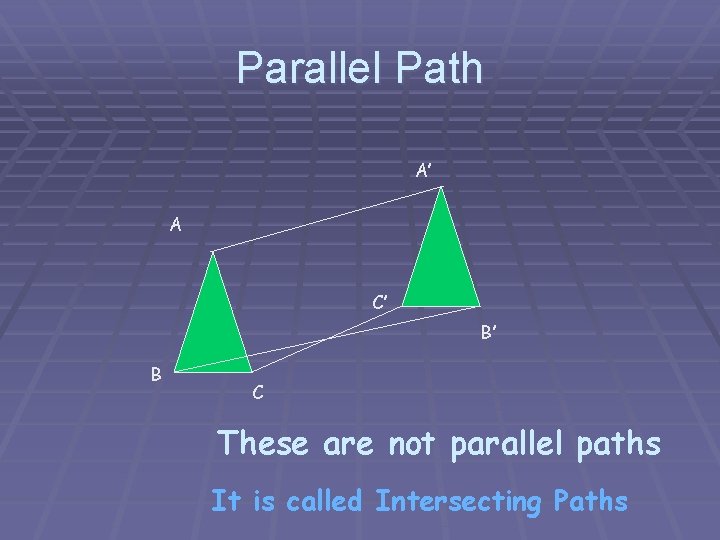
Parallel Path A’ A C’ B’ B C These are not parallel paths It is called Intersecting Paths

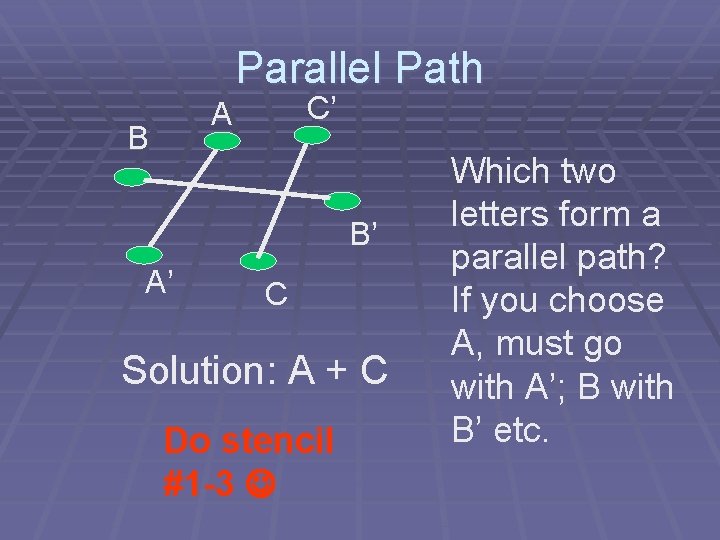
Parallel Path C’ A B B’ A’ C Solution: A + C Do stencil #1 -3 Which two letters form a parallel path? If you choose A, must go with A’; B with B’ etc.

Isometry § It is a transformation where a starting figure and the final figure are congruent. § Congruent: equal in every aspect (side and angle)

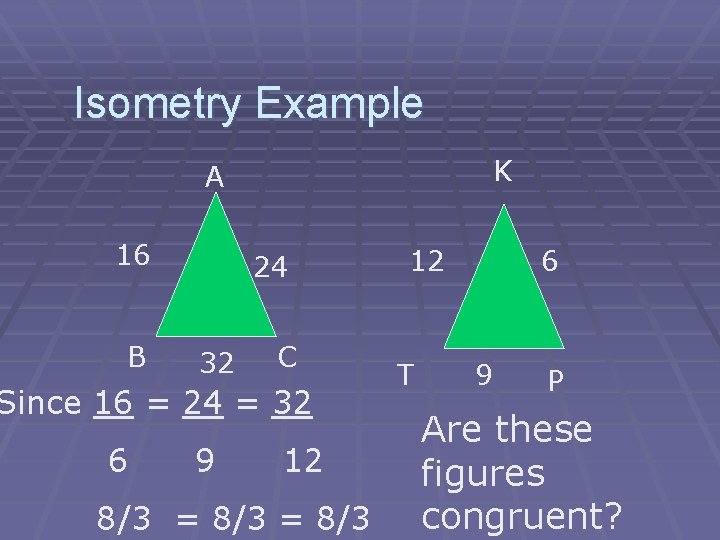
Isometry Example K A 16 B 24 32 C Since 16 = 24 = 32 6 9 12 8/3 = 8/3 12 T 6 9 P Are these figures congruent?

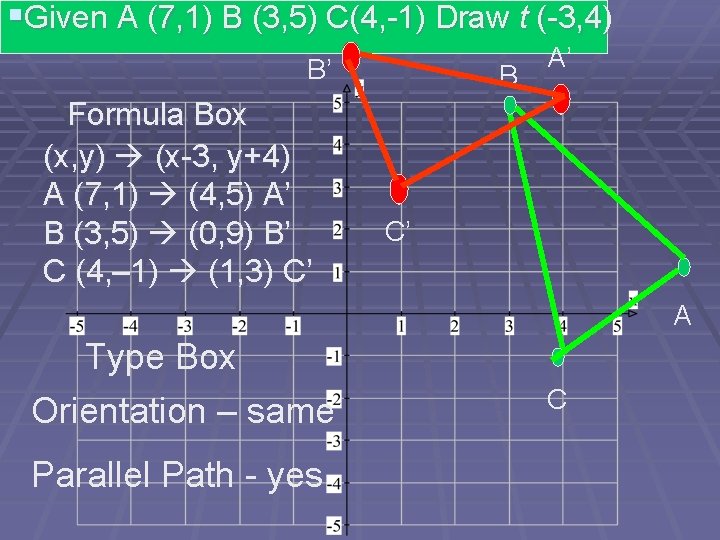
Translation § Sometimes called a slide or glide § Formula t (a, b) § Means (x, y) (x + a, y + b) § Eg t (-3, 4) § Eg Given A (7, 1) B (3, 5) C(4, -1) § Draw t (-3, 4) Include formula box and type box on graph § Type box means label and answer orientation (same / changed) § Parallel Path (yes / no)

§Given A (7, 1) B (3, 5) C(4, -1) Draw t (-3, 4) B’ Formula Box (x, y) (x-3, y+4) A (7, 1) (4, 5) A’ B (3, 5) (0, 9) B’ C (4, – 1) (1, 3) C’ B A’ C’ A Type Box Orientation – same Parallel Path - yes C

Rotation § In theory we need a rotation point § An angle § A direction § In practice – we use the origin as the rotation point § Angles of 90° and 180° § Direction cw and ccw § Note in math counterclockwise is positive

§ Formula § r (0, v) Rotation § Rotation Origin Angle & Direction § r (0, -90°) means a rotation about the origin 90° clockwise § (x, y) (y, -x) § When x becomes -x it changes sign. Thus – becomes +; + becomes – § Notice the new position of x and y.

Rotation § r (0, 90) means rotation about the origin 90° counterclockwise § (x, y) (-y, x) § r (0, 180) means rotation about the origin (direction does not matter) § (x, y) (-x, -y)

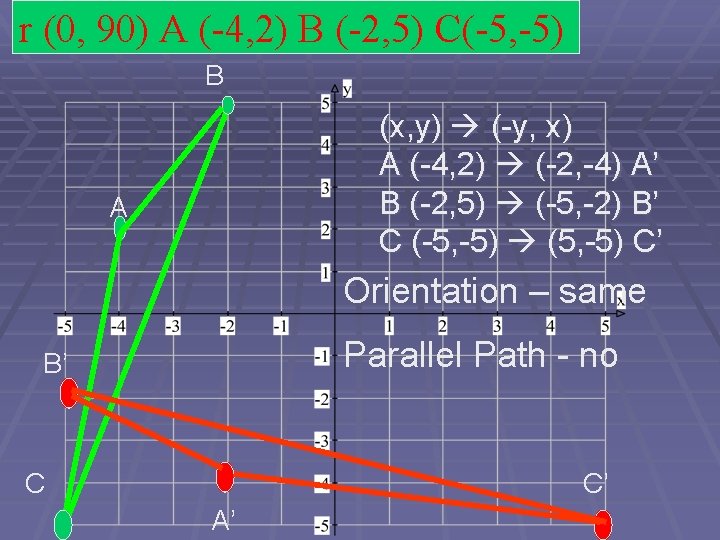
Rotation Practice § Given A (-4, 2) B (-2, 4) C (-5, 5) § Draw r (0, 90); include formula box on graph § You try it on a graph!

r (0, 90) A (-4, 2) B (-2, 5) C(-5, -5) B (x, y) (-y, x) A (-4, 2) (-2, -4) A’ B (-2, 5) (-5, -2) B’ C (-5, -5) (5, -5) C’ A Orientation – same Parallel Path - no B’ C C’ A’

Reflections § In theory we need a reflection line § Sx = reflection over x axis § (x, y) (x, -y) § Sy = reflection over y axis § (x, y) (-x, y) § S reflection over y = x § (x, y) (y, x) § S reflection over y = -x § (x, y) (-y, -x)

Memory Aid § It is very important to put all these formulas on one page. § P 160 #7 Put on separate sheet § P 161 #9 § You should be able to do all these transformation and understand how they work.

Combination Notation § When we perform two or more transformations we use the symbol ° § It means after §A°B § Means A after B § t (-3, 2) ° Sy means § A translation after a reflection (you must start backwards!)

Combination Glide Reflection § Draw t (-3, 2) ° Sy § (x, y) (-x, y) (x-3, y+2) § A (4, 3) (-4, 3) A’ (-7, 5) A’’ § A (4, 3) B (1, -3) (-1, -3) B’ (-4, -1) B’’ § C (-1, 2) (1, 2) C’ (-2, 4) C’’ § Orientation changed, Parallel Path no § What kind of isometry is this? It is a GLIDE REFLECTION § Let us look at the four types of isometries

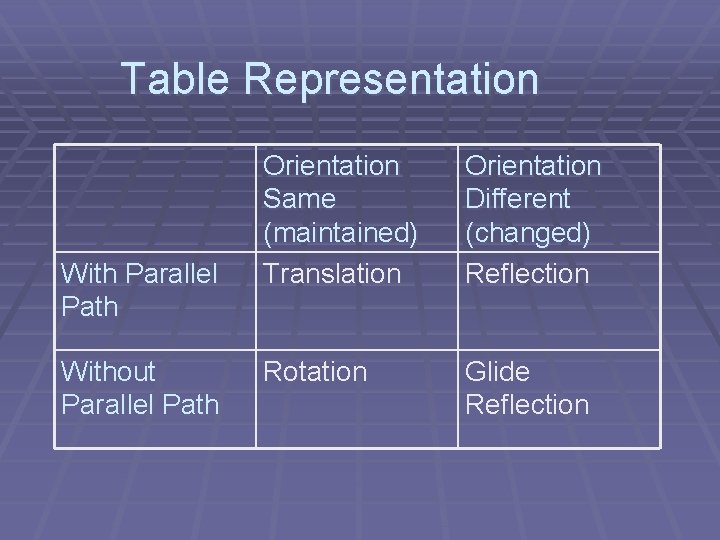
Single Isometry § Any transformation in the plane that preserves the congruency can be defined by a single isometry. Orientation Same? Parallel Path? YES No No TRANSLATION ROTATION REFLECTION GLIDE REFLECTION

Table Representation With Parallel Path Without Parallel Path Orientation Same (maintained) Translation Orientation Different (changed) Reflection Rotation Glide Reflection

Similtudes & Dilitations § When a transformation changes the size of an object but not its shape, we say it is a similtude or a dilitation. § Note – we observe size by side length and shape by angles § The similar shape we will create will have the same angle measurement and the sides will be proportional. § The 1 st part we need is this proportionality constant or scale factor.

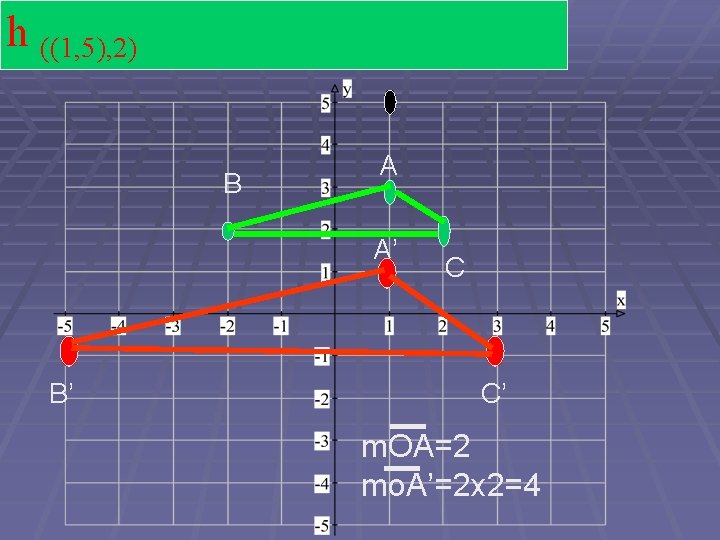
Similtudes & Dilitations § The 2 nd part we need is a point from which this increase or decrease in size will occur. § Note – this is an exercise in measuring so there can be some variation § Consider transform ABC by a factor of 2 about point 0 (1, 5). § The scale factor is sometimes called k

Similtudes & Dilitations § Sign of the scale factor § Positive – both figures (original & new) are on the same side of point § Negative – both figures (original and new) are on the opposite sides of point § The point is sometimes called the hole point

h ((1, 5), 2) B A A’ B’ C C’ m. OA=2 mo. A’=2 x 2=4

Other Examples § P 23 Example #8 § P 24 Spider Web § Discuss scale factor Beam or light beam method