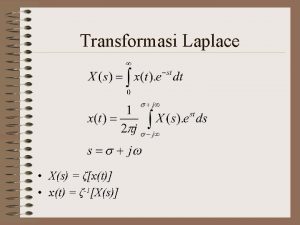The Laplace Equation Chris Olm and Johnathan Wensman

Introduction (Part I) n n We are going to be solving the Laplace equation

Introduction (Part II) n We will then demonstrate how to apply boundary conditions to

The Laplace Equation n Cartesian coordinates – V is potential – Harmonic! n Spherical

Azimuthal Symmetry Assuming azimuthal symmetry simplifies the system n In this case, decoupling V

Potential Function Want our function in terms of r and θ n So n

ODEs! n Plugging in we get: – These two ODEs that must be equal

General Solution for R(r) n Assume – Plugging in we get So – We

General Solution for Θ(θ) n Legendre polynomials – The solutions to the Legendre differential

The General Solution for V n Putting together R(r), Θ(θ) and summing over all

Example 1 n The potential is specified on a hollow sphere of radius R

Applying boundary conditions and intuition n We know it must take the form And

Yes! But doing so is tricky n First we note that the Legendre polynomials

Applying this property n We can multiply our general solution by Pl’’(cos θ) sin

Solving a particular case n n We could plug this into our equation giving

The better way n Instead let’s use the half angle formula to rewrite our

Getting the final answer n Plugging these into our general solution we get

Example 2 n n n Very similar to the first example The potential is

Proceeding as before n n n Must be of the form All Al must

Fourier’s Trick again n n By applying Fourier’s Trick again we can solve for

Conclusion n n By solving for the general solution we can easily solve for

References n n n 1)Griffiths, David. Introduction to Electrodynamics. 3 rd ed. Upper Saddle

Slides: 24

Download presentation

The Laplace Equation Chris Olm and Johnathan Wensman December 3, 2008

Introduction (Part I) n n We are going to be solving the Laplace equation in the context of electrodynamics Using spherical coordinates assuming azimuthal symmetry – Could also be solving in Cartesian or cylindrical coordinates – These would be applicable to systems with corresponding symmetry n Begin by using separation of variables n Use of Legendre polynomials to find the general solution – Changes the system of partial differential equations to ordinary differential equations

Introduction (Part II) n We will then demonstrate how to apply boundary conditions to the general solution to attain particular solutions – Explain and demonstrate using “Fourier’s Trick” – Analyzing equations to give us a workable solution

The Laplace Equation n Cartesian coordinates – V is potential – Harmonic! n Spherical coordinates – r is the radius – is the angle between the z-axis and the vector we’re considering – is the angle between the x-axis and our vector

Azimuthal Symmetry Assuming azimuthal symmetry simplifies the system n In this case, decoupling V from Φ n becomes

Potential Function Want our function in terms of r and θ n So n – Where R is dependent on r – Θ is dependent on θ

ODEs! n Plugging in we get: – These two ODEs that must be equal and. opposite: ↓ ↓

General Solution for R(r) n Assume – Plugging in we get So – We can deduce that the equation is solved when k=l or k=-(l+1) – So our general solution for R(r) is

General Solution for Θ(θ) n Legendre polynomials – The solutions to the Legendre differential equation, where l is an integer – Orthogonal – Most simply derived using Rodriques’s formula: n In our case x=cosθ so

The General Solution for V n Putting together R(r), Θ(θ) and summing over all l becomes

Applying the general solution

Example 1 n The potential is specified on a hollow sphere of radius R What is the potential on the inside of the sphere?

Applying boundary conditions and intuition n We know it must take the form And on the surface of the sphere must be V 0, also all Bl must be 0, so we get The question becomes are there any Al which satisfy this equation?

Yes! But doing so is tricky n First we note that the Legendre polynomials are a complete set of orthogonal functions – This has a couple consequences we can exploit

Applying this property n We can multiply our general solution by Pl’’(cos θ) sin θ and integrate (Fourier’s Trick)

Solving a particular case n n We could plug this into our equation giving In scientific terms this is unnecessarily cumbersome (in layman's terms this is a hard integral we don’t want or need to do)

The better way n Instead let’s use the half angle formula to rewrite our potential as n Plugging THIS into our equation gives n Now we can practically read off the values of Al

Getting the final answer n Plugging these into our general solution we get

Example 2 n n n Very similar to the first example The potential is specified on a hollow sphere of radius R What is the potential on the outside of the sphere?

Proceeding as before n n n Must be of the form All Al must be 0 this time, and again at the surface must be V 0, so and

Fourier’s Trick again n n By applying Fourier’s Trick again we can solve for Bl As far as we can solve without a specific potential

Conclusion n n By solving for the general solution we can easily solve for the potential of any system easily described in spherical coordinates This is useful as the electric field is the gradient of the potential – The electric field is an important part of electrostatics

References n n n 1)Griffiths, David. Introduction to Electrodynamics. 3 rd ed. Upper Saddle River: Prentice Hall, 1999. 2)Blanchard, Paul, Robert Devaney, and Glen Hall. Differential equations. 3 rd ed. Belmont: Thomson Higher Education, 2006. 3) White, J. L. , “Mathematical Methods Special Functions Legendre’s Equation and Legendre Polynomials, ” http: //www. tmt. ugal. ro/crios/Support/ANPT/Curs/math/s 8 l egd/s 8 legd. html, accessed 12/2/2008. 4) Weisstein, Eric W. "Laplace's Equation--Spherical Coordinates. " From Math. World--A 5) Wolfram Web Resource. http: //mathworld. wolfram. com/Laplaces. Equation. Spherical. Coor dinates. html, accessed 12/2/2008