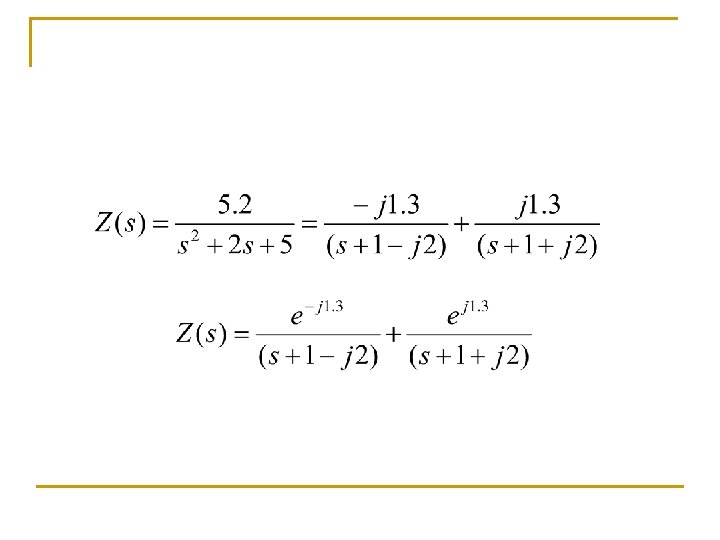LAPLACE TRANSFORMS INTRODUCTION The Laplace Transformation Time Domain



























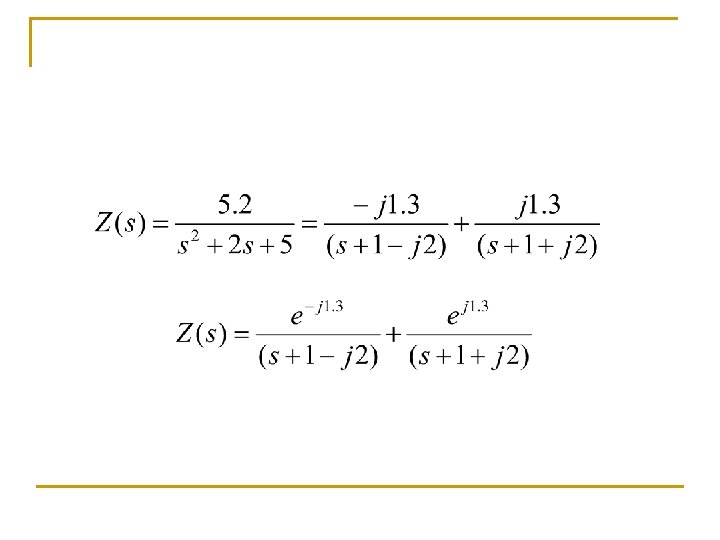
- Slides: 29

LAPLACE TRANSFORMS

INTRODUCTION

The Laplace Transformation Time Domain Frequency Domain Laplace Transform Differential equations Algebraic equations Input excitation e(t) Output response r(t) Input excitation E(s) Output response R(s) Inverse Laplace Transform

THE LAPLACE TRANSFORM


THE INVERSE LAPLACE TRANSFORM


Functional Laplace Transform Pairs

Operational Laplace Transform Pairs

Inverse Laplace Transform n The inverse Laplace transform is usually more difficult than a simple table conversion.

Partial Fraction Expansion n If we can break the right-hand side of the equation into a sum of terms and each term is in a table of Laplace transforms, we can get the inverse transform of the equation (partial fraction expansion).

Repeated Roots n In general, there will be a term on the righthand side for each root of the polynomial in the denominator of the left-hand side. Multiple roots for factors such as (s+2)n will have a term for each power of the factor from 1 to n.

Complex Roots n Complex roots are common, and they always occur in conjugate pairs. The two constants in the numerator of the complex conjugate terms are also complex conjugates. where K* is the complex conjugate of K.

Solution of Partial Fraction Expansion n The solution of each distinct (non-multiple) root, real or complex uses a two step process. q q The first step in evaluating the constant is to multiply both sides of the equation by the factor in the denominator of the constant you wish to find. The second step is to replace s on both sides of the equation by the root of the factor by which you multiplied in step 1


The partial fraction expansion is:

n The inverse Laplace transform is found from the functional table pairs to be:

Repeated Roots n n Any unrepeated roots are found as before. The constants of the repeated roots (s-a)m are found by first breaking the quotient into a partial fraction expansion with descending powers from m to 0:

n The constants are found using one of the following:


The partial fraction expansion yields:

The inverse Laplace transform derived from the functional table pairs yields:

A Second Method for Repeated Roots Equating like terms:

Thus

Another Method for Repeated Roots As before, we can solve for K 2 in the usual manner.


Unrepeated Complex Roots n n Unrepeated complex roots are solved similar to the process for unrepeated real roots. That is you multiply by one of the denominator terms in the partial fraction and solve for the appropriate constant. Once you have found one of the constants, the other constant is simply the complex conjugate.

Complex Unrepeated Roots