Capacitance and Laplaces Equation Capacitance Definition Simple Capacitance

Capacitance and Laplace’s Equation • Capacitance Definition • Simple Capacitance Examples • Capacitance Example using Streamlines & Images – Two-wire Transmission Line – Conducting Cylinder/Plane • Field Sketching • Laplace and Poison’s Equation • Laplace’s Equation Examples • Laplace’s Equation - Separation of variables • Poisson’s Equation Example

Potential of various charge arrangements •

Basic Capacitance Definition A simple capacitor consists of two oppositely charged conductors surrounded by a uniform dielectric. An increase in Q by some factor results in an increase D (and E) by same factor. With the potential difference between conductors: S Q . A increasing by the same factor -- so the ratio Q to V 0 is constant. We define the capacitance of the structure as the ratio of stored charge to applied voltage, or Units are Coul/V or Farads -Q . B E, D

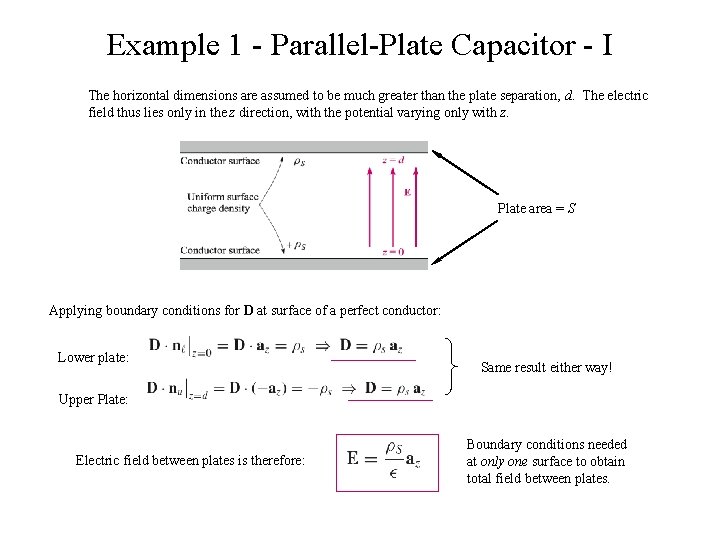
Example 1 - Parallel-Plate Capacitor - I The horizontal dimensions are assumed to be much greater than the plate separation, d. The electric field thus lies only in the z direction, with the potential varying only with z. Plate area = S Applying boundary conditions for D at surface of a perfect conductor: Lower plate: Same result either way! Upper Plate: Electric field between plates is therefore: Boundary conditions needed at only one surface to obtain total field between plates.

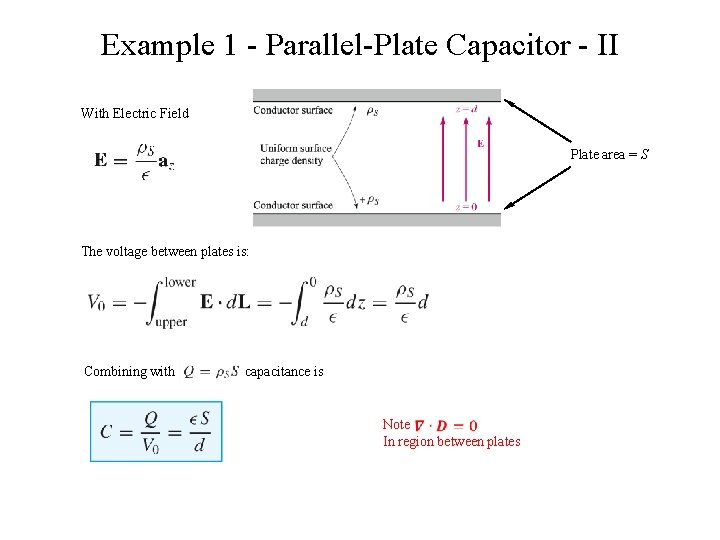
Example 1 - Parallel-Plate Capacitor - II With Electric Field Plate area = S The voltage between plates is: Combining with capacitance is Note In region between plates

Energy Stored in parallel-plate Capacitor Stored energy is found by integrating the energy density in the electric field over the capacitor volume. From Chapter 4 page 102 Rearranging gives S C Gives 3 ways of stored energy: V 0 2

Example 2 - Coaxial Transmission Line - I Coaxial Electric Field using Gauss’ Law: S Writing with surface-charge density E 1 assume a unit length in z Simplifying E = 0 elsewhere, assuming hollow inner conductor, equal and opposite charges on inner and outer conductors.

Example 2 - Coaxial Transmission Line - II Electric Field between conductors S Potential difference between conductors: E 1 assume unit length in z Charge per unit length on inner conductor Gives capacitance:

Example 3 – Concentric Spherical Capacitor Two concentric spherical conductors of radii a and b, with equal and opposite charges Q on inner and outer conductors. From Gauss’ Law, electric field exists only between spheres and is given by: E Q a -Q b Potential difference between inner and outer spheres is Capacitance is thus: Note as (isolated sphere)

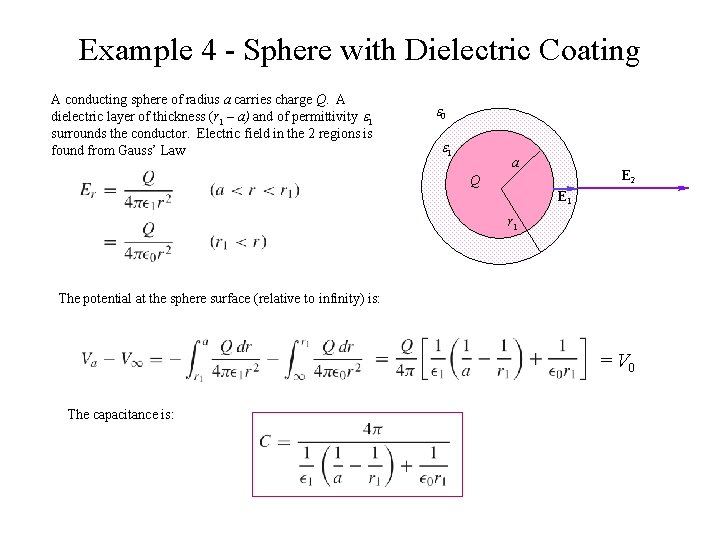
Example 4 - Sphere with Dielectric Coating A conducting sphere of radius a carries charge Q. A dielectric layer of thickness (r 1 – a) and of permittivity 1 surrounds the conductor. Electric field in the 2 regions is found from Gauss’ Law a Q E 2 E 1 r 1 The potential at the sphere surface (relative to infinity) is: = V 0 The capacitance is:

Example 5 – Parallel Capacitor with 2 -Layer Dielectric Surface charge on either plate is normal displacement DN through both dielectrics: Potential between top and bottom surfaces The capacitance is thus: << Rule for 2 capacitors in series

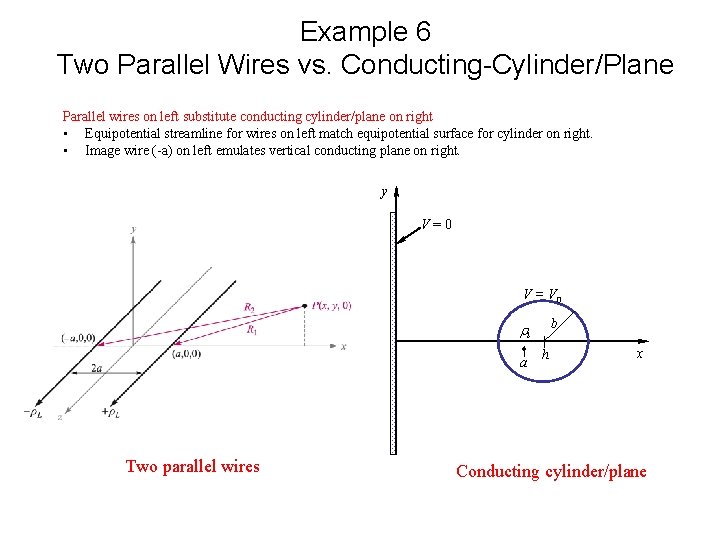
Example 6 Two Parallel Wires vs. Conducting-Cylinder/Plane Parallel wires on left substitute conducting cylinder/plane on right • Equipotential streamline for wires on left match equipotential surface for cylinder on right. • Image wire (-a) on left emulates vertical conducting plane on right. y V=0 V = V 0 . b l a Two parallel wires h x Conducting cylinder/plane

Example 6 - Two Parallel Wires and Conducting-Cylinder/Plane • Parallel Wires 1. Superimpose 2 long-wire potentials at x = +a and x = -a. 2. Translate to common rectangular coordinate system. 3. Define parameter K (=constant) for V (=constant) equipotential. 4. Find streamlines (x, y) for constant K and constant V. • Conducting-Cylinder/Plane 1. Insert metal cylinder along equipotential (constant K) streamline. 2. Work backward to find long-wire position, charge density, and K parameter from cylinder diameter, offset, and V potential. 3. Calculate capacitance of cylinder/plane from long-wire position and charge density 4. Write expression for potential, D, and E fields between cylinder and plane. 5. Write expression for surface charge density on plane.

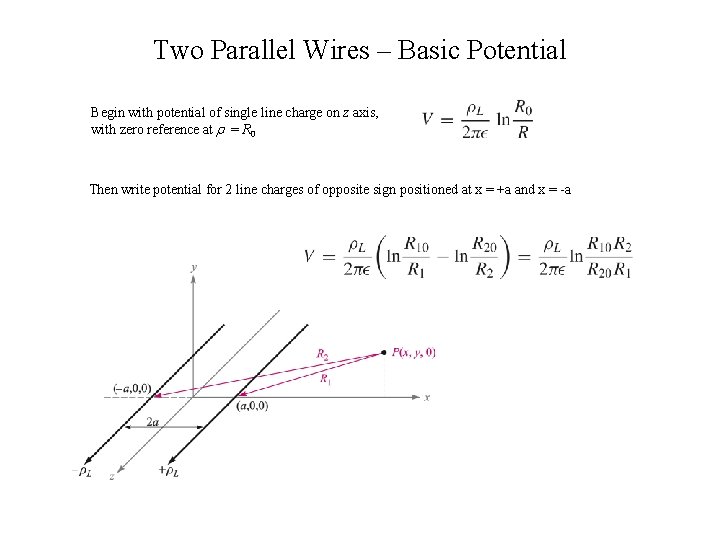
Two Parallel Wires – Basic Potential Begin with potential of single line charge on z axis, with zero reference at = R 0 Then write potential for 2 line charges of opposite sign positioned at x = +a and x = -a

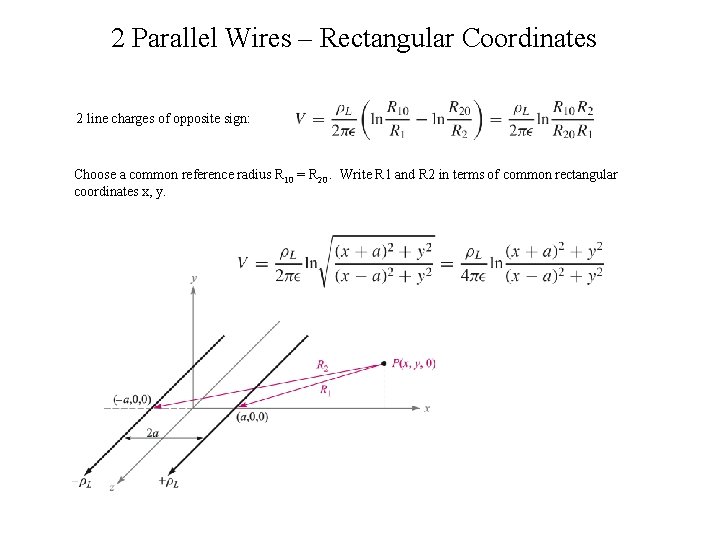
2 Parallel Wires – Rectangular Coordinates 2 line charges of opposite sign: Choose a common reference radius R 10 = R 20. Write R 1 and R 2 in terms of common rectangular coordinates x, y.

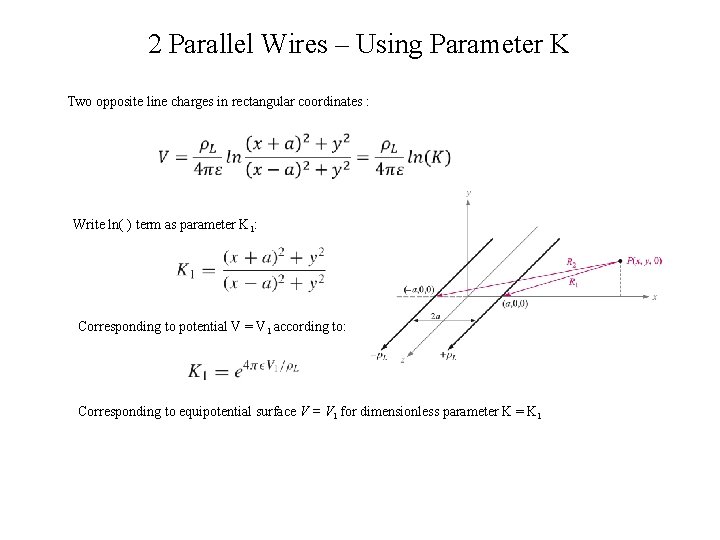
2 Parallel Wires – Using Parameter K Two opposite line charges in rectangular coordinates : Write ln( ) term as parameter K 1: Corresponding to potential V = V 1 according to: Corresponding to equipotential surface V = V 1 for dimensionless parameter K = K 1

2 Parallel Wires – Getting Streamlines for K Find streamlines for constant parameter K 1 where voltage is constant V 1 y V=0 To better identify surface, expand the squares, and collect terms: V = V 0 l a h Equation of circle (cylinder) with radius b and displaced along x axis h b x

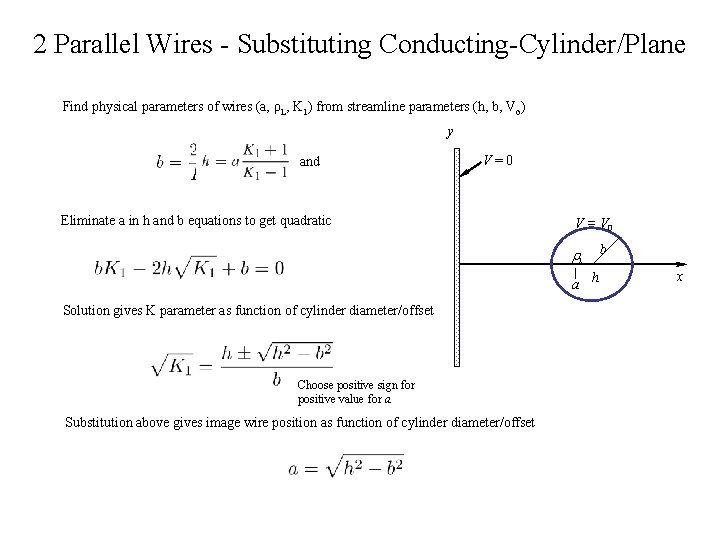
2 Parallel Wires - Substituting Conducting-Cylinder/Plane Find physical parameters of wires (a, ρL, K 1) from streamline parameters (h, b, Vo) y and V=0 Eliminate a in h and b equations to get quadratic V = V 0 l a h Solution gives K parameter as function of cylinder diameter/offset Choose positive sign for positive value for a Substitution above gives image wire position as function of cylinder diameter/offset b x

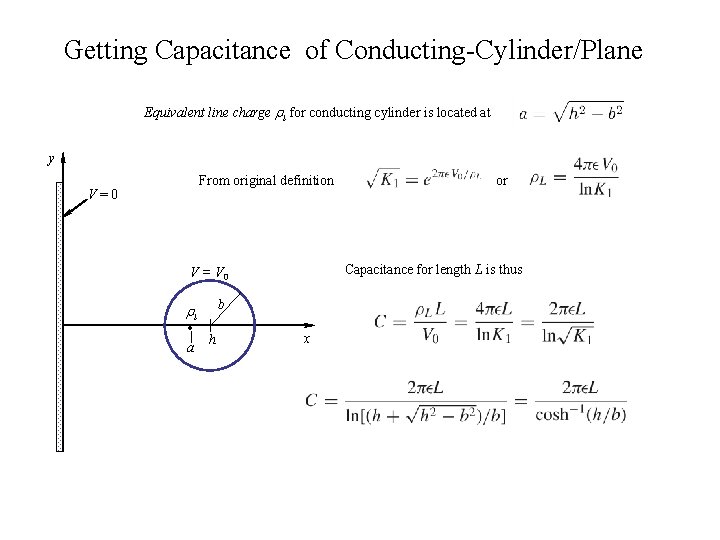
Getting Capacitance of Conducting-Cylinder/Plane Equivalent line charge l for conducting cylinder is located at y From original definition V=0 Capacitance for length L is thus V = V 0 . b l a h or x

Example 1 - Conducting Cylinder/Plane Conducting cylinder radius b = 5 mm, offset h = 13 mm, potential V 0 = 100 V. Find offset of equivalent line charge a, parameter K, charge density l , and capacitance C. y V=0 mm V = V 0 . b l a h x Charge density and capacitance Results unchanged so long as relative proportions maintained

Example 2 - Conducting Cylinder/Plane For V 0 = 50 -volt equipotential surface we recalculate cylinder radius and offset mm mm The resulting surface is the dashed red circle

Getting Fields for Conducting Cylinder/Plane • y V=0 V = V 0 l b a h x

Getting Capacitance of 2 -Wire or 2 -Cylinder Line With two wires or cylinders (and zero potential plane between them) the structure represents two wire/plane or two cylinder/plane capacitors in series, so the overall capacitance is half that derived previously. b h Finally, if the cylinder (wire) dimensions are much less than their spacing (b << h), then L x

Using Field Sketches to Estimate Capacitance This method employs these properties of conductors and fields:

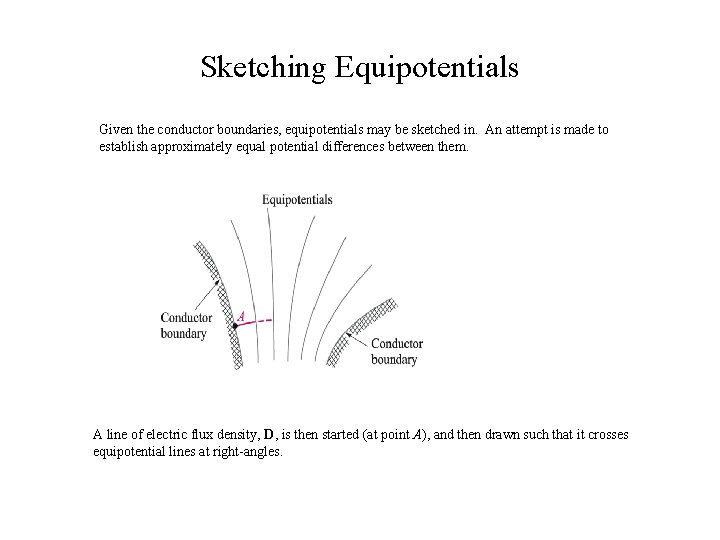
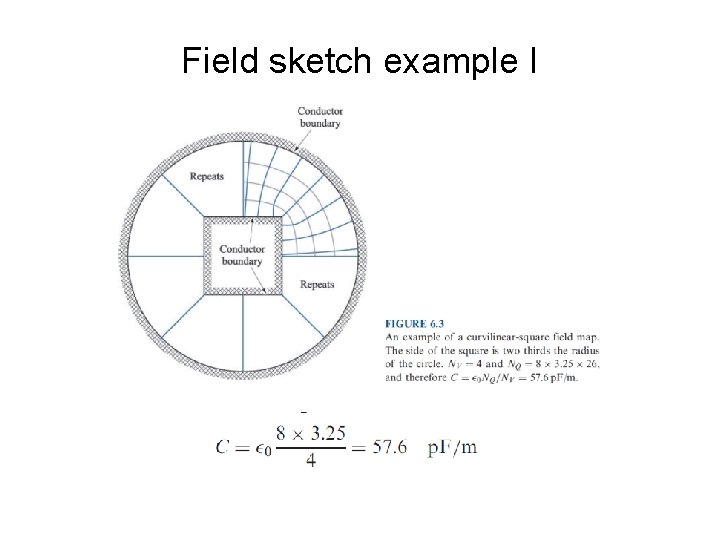
Sketching Equipotentials Given the conductor boundaries, equipotentials may be sketched in. An attempt is made to establish approximately equal potential differences between them. A line of electric flux density, D, is then started (at point A), and then drawn such that it crosses equipotential lines at right-angles.

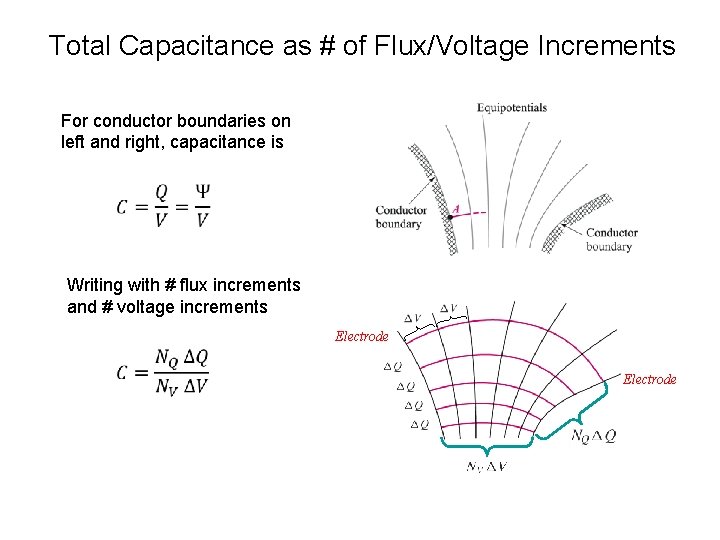
Total Capacitance as # of Flux/Voltage Increments For conductor boundaries on left and right, capacitance is Writing with # flux increments and # voltage increments Electrode

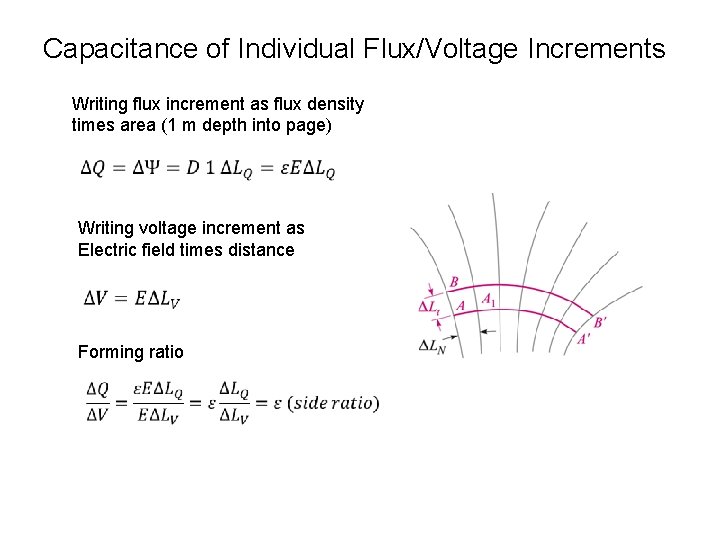
Capacitance of Individual Flux/Voltage Increments Writing flux increment as flux density times area (1 m depth into page) Writing voltage increment as Electric field times distance Forming ratio

Total Capacitance for Square Flux/Voltage Increments Capacitance between conductor boundaries Combining with flux/voltage ratio Provided ΔLQ = ΔLV (increments square)

Field sketch example I

Field Sketch Example II

Laplace and Poisson’s Equation 1. Assert the obvious – Laplace - Flux must have zero divergence in empty space, consistent with geometry (rectangular, cylindrical, spherical) – Poisson - Flux divergence must be related to free charge density 2. This provides general form of potential and field with unknown integration constants. 3. Fit boundary conditions to find integration constants.

Derivation of Poisson’s and Laplace’s Equations These equations allow one to find the potential field in a region, in which values of potential or electric field are known at its boundaries. Start with Maxwell’s first equation: where and so that or finally:

Poisson’s and Laplace’s Equations (continued) Recall the divergence as expressed in rectangular coordinates: …and the gradient: then: . It is known as the Laplacian operator

Summary of Poisson’s and Laplace’s Equations we already have: which becomes: This is Poisson’s equation, as stated in rectangular coordinates. In the event that there is zero volume charge density, the right-hand-side becomes zero, and we obtain Laplace’s equation:

Laplacian Operator in Three Coordinate Systems (Laplace’s equation)

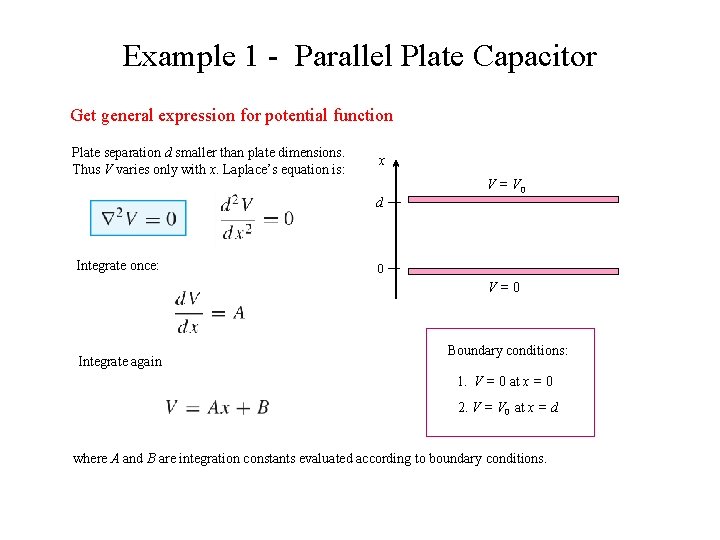
Example 1 - Parallel Plate Capacitor Get general expression for potential function Plate separation d smaller than plate dimensions. Thus V varies only with x. Laplace’s equation is: x V = V 0 d Integrate once: 0 V=0 Integrate again Boundary conditions: 1. V = 0 at x = 0 2. V = V 0 at x = d where A and B are integration constants evaluated according to boundary conditions.

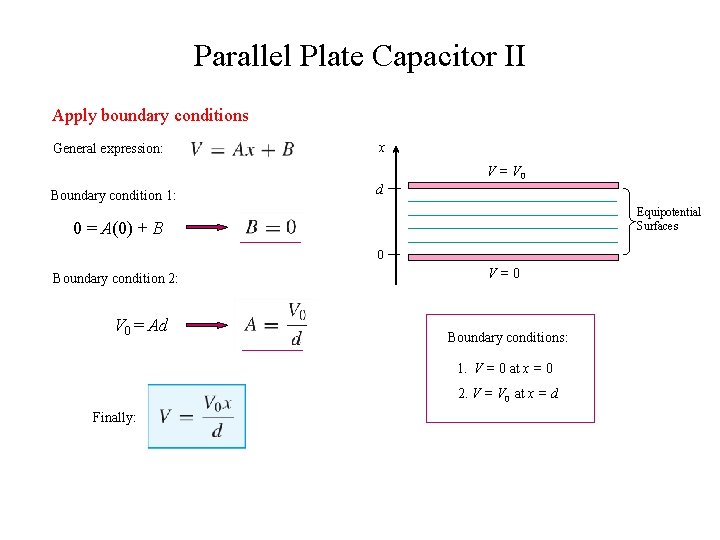
Parallel Plate Capacitor II Apply boundary conditions General expression: x V = V 0 Boundary condition 1: d Equipotential Surfaces 0 = A(0) + B 0 Boundary condition 2: V 0 = Ad V=0 Boundary conditions: 1. V = 0 at x = 0 2. V = V 0 at x = d Finally:

Parallel Plate Capacitor III Getting 1) Electric field, 2) Displacement, 3) Charge density, 4) Capacitance Potential x Electric Field Surface Area = S V = V 0 d + + + + E n Displacement 0 - - - - V=0 At the lower plate n = ax Conductor boundary condition Total charge on lower plate capacitance Equipotential Surfaces

Example 2 - Coaxial Transmission Line Get general expression for potential V varies with radius only, Laplace’s equation is: ( > 0) V 0 V=0 E L Integrate once: Boundary conditions: Integrate again: 1. 2. V = 0 at b V = V 0 at a

Coaxial Transmission Line II Apply boundary conditions General Expression Boundary condition 1: V 0 V=0 E L Boundary condition 2: Combining: Boundary conditions: 1. 2. V = 0 at b V = V 0 at a

Coaxial Transmission Line III Getting 1) Electric field, 2) Displacement, 3) Charge density, 4) Capacitance Potential: Electric Field: V 0 V=0 E Charge density on inner conductor: Total charge on inner conductor: L Capacitance:

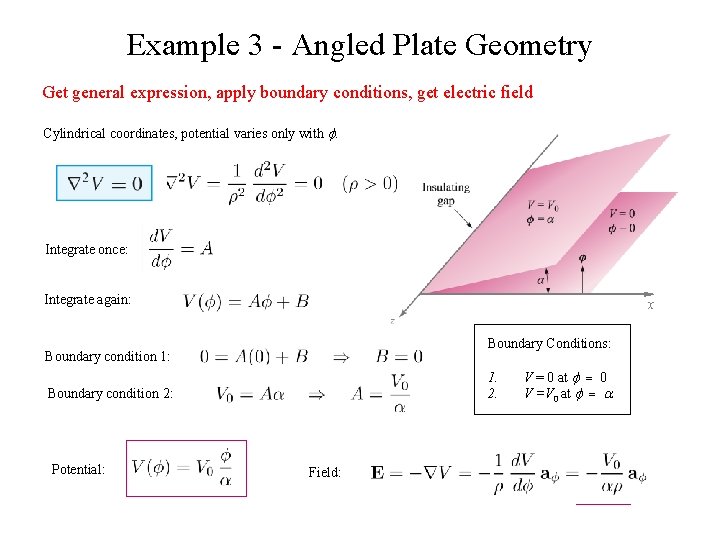
Example 3 - Angled Plate Geometry Get general expression, apply boundary conditions, get electric field Cylindrical coordinates, potential varies only with Integrate once: Integrate again: x Boundary Conditions: Boundary condition 1: 1. 2. Boundary condition 2: Potential: Field: V = 0 at 0 V =V 0 at

Example 4 - Concentric Sphere Geometry Get general expression, apply boundary conditions V varies only with radius. Laplace’s equation: V=0 E or: V 0 a b Integrate once: Integrate again: Boundary Conditions: Boundary condition 1: 1. 2. Boundary condition 2: Potential: V = 0 at r = b V = V 0 at r = a

Concentric Sphere Geometry II Get 1) electric field, 2) displacement, 3) charge density, 4) capacitance Potential: V=0 (a < r < b) Electric field: E V 0 a b Charge density on inner conductor: Total charge on inner conductor: Capacitance:

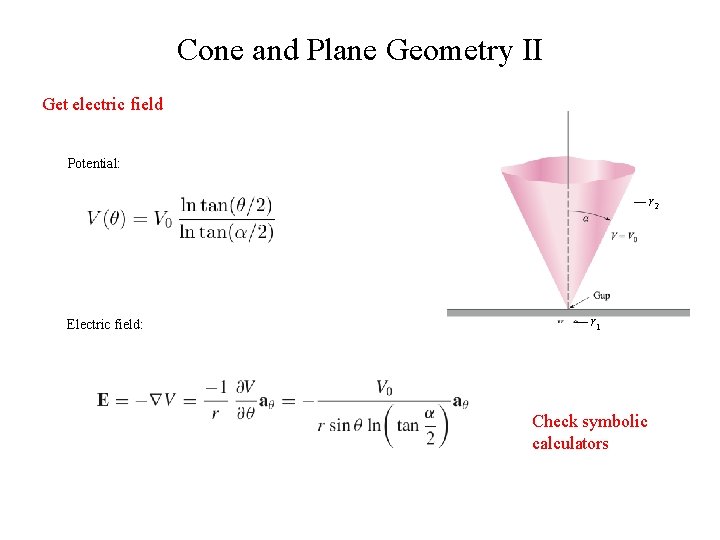
Example 5 – Cone and Plane Geometry Get general expression, apply boundary conditions V varies only with only, Laplace’s equation is: R, > 0 Integrate once: Integrate again Boundary Conditions: Boundary condition 1: 1. 2. Boundary condition 2: Potential: V = 0 at V = V 0 at

Cone and Plane Geometry II Get electric field Potential: r 2 Electric field: r 1 Check symbolic calculators

Cone and Plane Geometry III Get 1) charge density, 2) capacitance Charge density on cone surface: r 2 Total charge on cone surface: r 1 Capacitance: Note capacitance positive (as should be). Neglects fringing fields, important for smaller .

Example 6 – Product Solution in 2 Dimensions

Product Solution in 2 Dimensions II Paul Lorrain and Dale Corson, “Electromagnetic Fields and Waves” 2 nd Ed, W. H. Freeman, 1970

Product Solution in 2 Dimensions III

Product Solution in 2 Dimensions IV This problem just keeps on going!

Product Solution in 2 Dimensions V

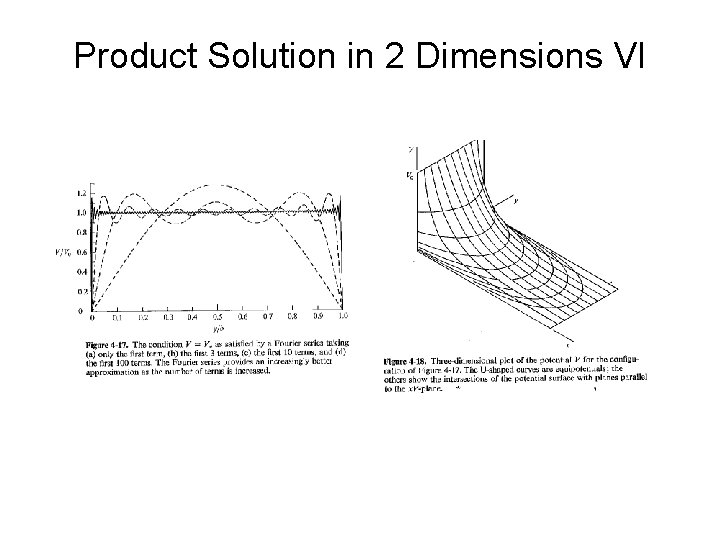
Product Solution in 2 Dimensions VI

Example 7 – Another Product Solution in 2 Dimensions

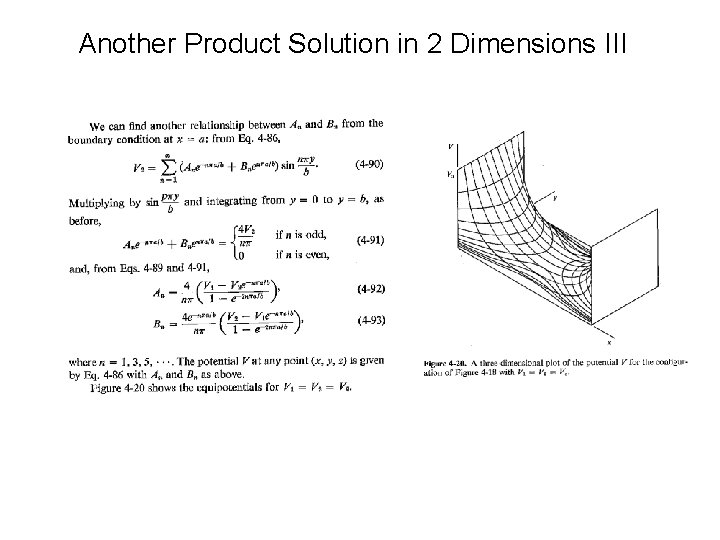
Another Product Solution in 2 Dimensions II

Another Product Solution in 2 Dimensions III

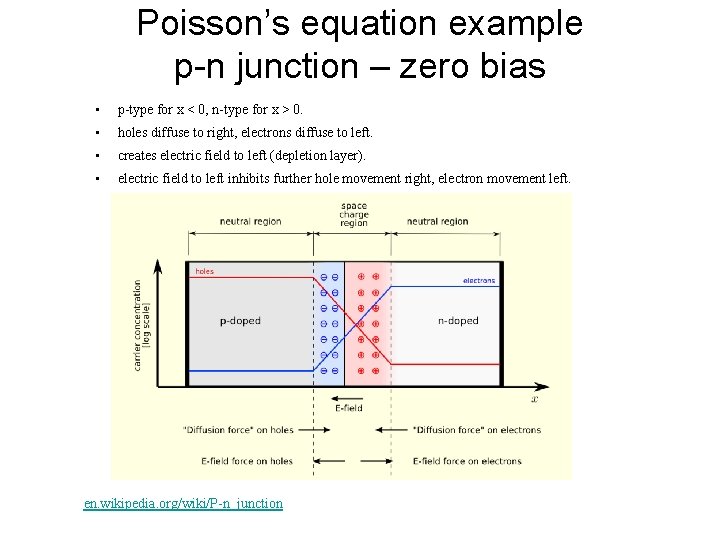
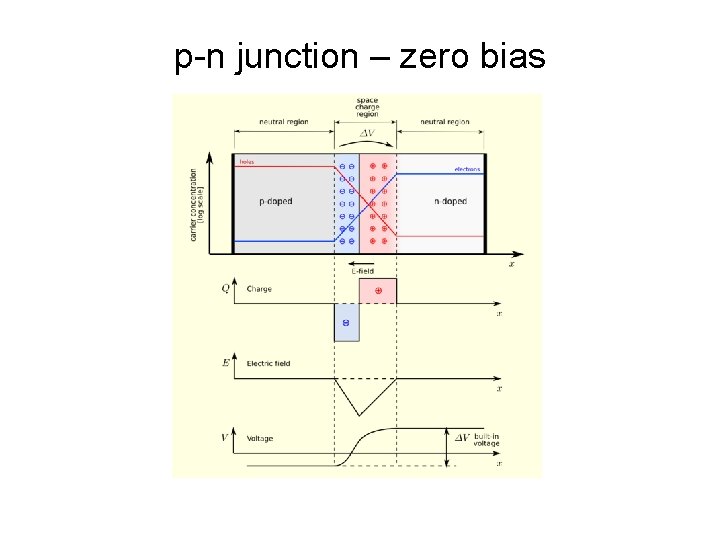
Poisson’s equation example p-n junction – zero bias • p-type for x < 0, n-type for x > 0. • holes diffuse to right, electrons diffuse to left. • creates electric field to left (depletion layer). • electric field to left inhibits further hole movement right, electron movement left. en. wikipedia. org/wiki/P-n_junction

p-n junction – zero bias

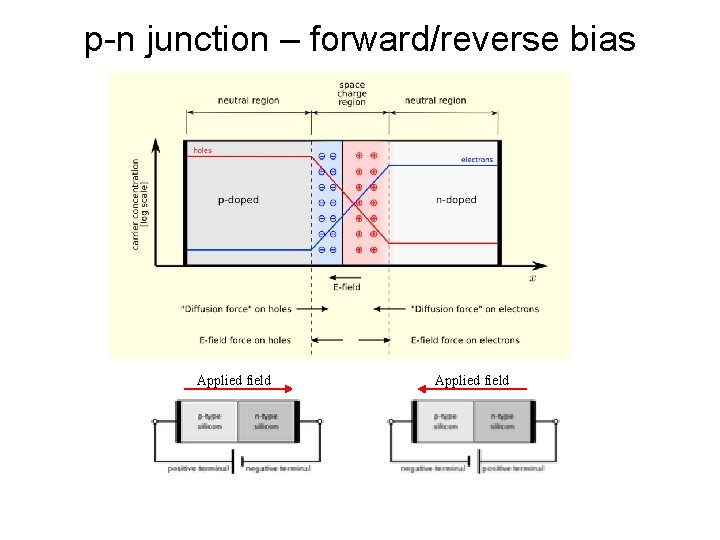
p-n junction – forward/reverse bias Applied field

p-n junction – charge, field, potential

p-n junction – Obtaining Electric Field

p-n junction – Obtaining Potential

p-n junction - Obtaining Charge

p-n junction Obtaining Junction Capacitance