Stochastic Order and Skyline 1 XUEMIN LIN WENJIE

Stochastic Order and Skyline 1 XUEMIN LIN, WENJIE ZHANG UNIVERSITY OF NEW SOUTH WALES Stocastic Order and Skyline Computation

Database Group@UNSW (2002 -) 4 faculty members : 3 2 Prof Xuemin Lin, Dr. John Shepherd, Dr. Wei Wang, Dr. Raymond Wong. 3 research fellows (research assistant Prof) Muhammad Aamir Cheema, Wenjie Zhang, Ying Zhang. 20+Ph. D students. Research Interests: core topics in DB, DM, IR, MM. DBG@UNSW

Outline 3 q. Skyline and its variants q. Why Stochastic Skyline q. Stochastic Order I: lower orthant order q Testing Lower Orthant Order q. Lower Orthant Order Enough? q. Stochastic Order II: Usual Order q. Testing Usual Order q. Stochastic Skyline Computation Stocastic Order and Skyline Computation

Skyline 4 鱼与熊掌不能兼得? What is the next? Stocastic Order and Skyline Computation

Searching Flights to Shanghai 5 Price, travel-time and # stops all matter! A (long) list of all feasible routes? boring to review Presenting only some selected flights – how? Sydney Shanghai ($1300, 10 hours, 0 stop) Good! Sydney Hongkong Shanghai ($1000, 15 hours, 1 stop) Also good, cheaper, though longer travel time and more stops Sydney Singapore Tokyo Shanghai ($1800, 19 hours, 2 stops) Not good, more expensive, longer travel time, and more stops! Skyline routes – all possible trade-offs among price, travel-time and # stops that are superior to the others Stocastic Order and Skyline Computation

Skyline 6 Skyline: candidates of best options in multi-criteria decision applications. n-dimensional numeric space D = (D 1, …, Dn) on each dimension, a user preference ≻ is defined two points, u dominates v (u ≻ v), if Di (1 ≤ i ≤ n), u. Di ≻= v. Di Dj (1 ≤ j ≤ n), u. Dj ≻ v. Dj Skyline: points not dominated by another point. Stocastic Order and Skyline Computation

Skyline 7 A skyline building is either close to the viewing point, or higher than those in front of it. Stocastic Order and Skyline Computation

Computing Full Skyline 8 Divide-and-conquer and block nested loops by Borzsonyi et al [ICDE’ 01]. Sort-first-skyline (SFS) by Chomicki et al [ICDE’ 03]. Improved by LESS [VLDB’ 05]. Using bitmaps and the relationships between the skyline and the minimum coordinates of individual points, by Tan et al [VLDB’ 01]. Using nearest-neighbor search by Kossmann et al [VLDB’ 02]. The progressive branch-and-bound method by Papadias et al [SIGMOD’ 03]. Z-order[VLDB’ 07] … Stocastic Order and Skyline Computation

Subspace Skyline Computation 9 Sky cube – computing skylines in all non-empty subspaces (Yuan et al. , VLDB’ 05) Any subspace skyline queries can be answered (efficiently) Characterize sub-spaces (Pei et al. , VLDB’ 05) Combined (TODS’ 06) Supporting update? [Zhang et al, SIGMOD’ 06] Indexing Subspaces [Tao et al, ICDE’ 06] Speed-up skycube computation [Pei et al, ICDE’ 07] Subspace skyline: SUBSKY [ICDE’ 06] Stocastic Order and Skyline Computation

Variants 10 Skyline over Sliding windows (Lin et al. ICDE 04) Top k-dominating query [Papadias et al. SIGMOD’ 03 , Yiu et al. VLDB’ 07] k-dominating skyline objects [Chan et al. SIGMOD’ 06] Approximate Skyline [Koltun et. al. ICDT’ 05] Representative Skyline based on population (Lin et al: ICDE 07). Representation Skyline based on skyline topology (Tao et al. ICDE 09). Mining Preference from Examples (Jiang et al. KDD 08) Stocastic Order and Skyline Computation

Skylines on Uncertain Data 11 Consider game-by-game statistics Conventional methods compute the skyline on Aggregate: mean Limitations Affected by outliers Lose data distributions Probabilistic skylines An instance has a probability to represent the object An object has a probability to be in the skyline Stocastic Order and Skyline Computation

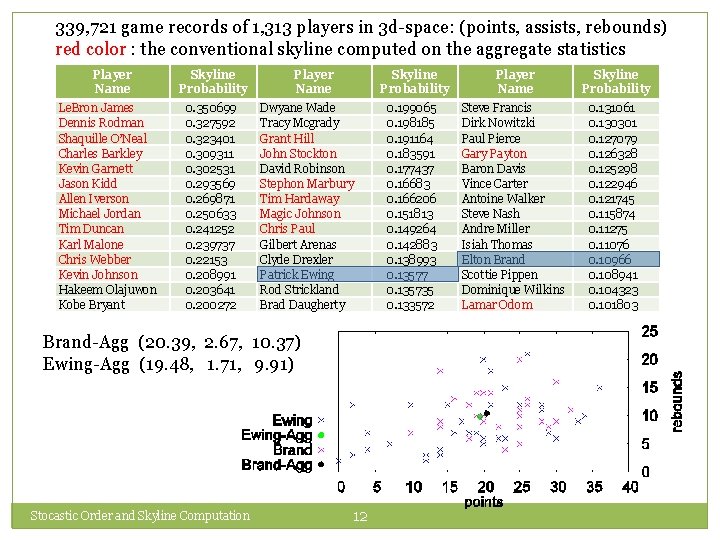
339, 721 game records of 1, 313 players in 3 d-space: (points, assists, rebounds) red color : the conventional skyline computed on the aggregate statistics Player Name Le. Bron James Dennis Rodman Shaquille O’Neal Charles Barkley Kevin Garnett Jason Kidd Allen Iverson Michael Jordan Tim Duncan Karl Malone Chris Webber Kevin Johnson Hakeem Olajuwon Kobe Bryant Skyline Probability 0. 350699 0. 327592 0. 323401 0. 309311 0. 302531 0. 293569 0. 269871 0. 250633 0. 241252 0. 239737 0. 22153 0. 208991 0. 203641 0. 200272 Player Name Skyline Probability Dwyane Wade Tracy Mcgrady Grant Hill John Stockton David Robinson Stephon Marbury Tim Hardaway Magic Johnson Chris Paul Gilbert Arenas Clyde Drexler Patrick Ewing Rod Strickland Brad Daugherty Brand-Agg (20. 39, 2. 67, 10. 37) Ewing-Agg (19. 48, 1. 71, 9. 91) Stocastic Order and Skyline Computation 12 0. 199065 0. 198185 0. 191164 0. 183591 0. 177437 0. 16683 0. 166206 0. 151813 0. 149264 0. 142883 0. 138993 0. 13577 0. 135735 0. 133572 Player Name Steve Francis Dirk Nowitzki Paul Pierce Gary Payton Baron Davis Vince Carter Antoine Walker Steve Nash Andre Miller Isiah Thomas Elton Brand Scottie Pippen Dominique Wilkins Lamar Odom Skyline Probability 0. 131061 0. 130301 0. 127079 0. 126328 0. 125298 0. 122946 0. 121745 0. 115874 0. 11275 0. 11076 0. 10966 0. 108941 0. 104323 0. 101803

Uncertain Objects 13 An uncertain object is represented as Continuous case: a probabilistic density function (PDF) Discrete case: a set of instances, each takes a probability to appear U = {u 1, …, un}, 0 < p(ui) ≤ 1 and 1≤i≤n p(ui) = 1 Without loss of generality, assume equal probability, p(ui) = 1 / |U| Stocastic Order and Skyline Computation

Skyline of Uncertain Objects 14 Probabilistic Skyline: (Pei et al. VLDB 07, Atallah et al. PODS 09, etc. Zhang et al. ICDE 2009) Skyline probabilities by possible worlds. Providing the probabilities not worse than any other objects. Provide minimal candidate set of optimal solutions? How to define optimal options? How to characterize the minimum candidate set? Stocastic Order and Skyline Computation

Expected Utility & Stochastic Order 15 Expected Utility Principle: Given a set U of uncertain objects and a decreasing utility function f, select U in U to maxmize E[f (U)]. Stochastic Order: Given a family ℱ of utility functions, U ≺ℱ V if for each f in ℱ E[f(U)] ≥ E [f(V)] Decreasing Multiplicative Functions: ℱ= where fi is nonnegative decreasing. Low orthant order: the stochastic order is defined over the family of decreasing multiplicative functions. Stocastic Order and Skyline Computation

16 Utility function: o : nonnegative decreasing Athlete Instance 1 /probability Instance 2 /probability A (1, 4) / 0. 5 (3, 2) / 0. 5 B (2, 5) / 0. 5 (4, 3) / 0. 5 C (5, 1) / 0. 01 (3, 4) / 0. 99 e. g. ; ; Stocastic Order and Skyline Computation

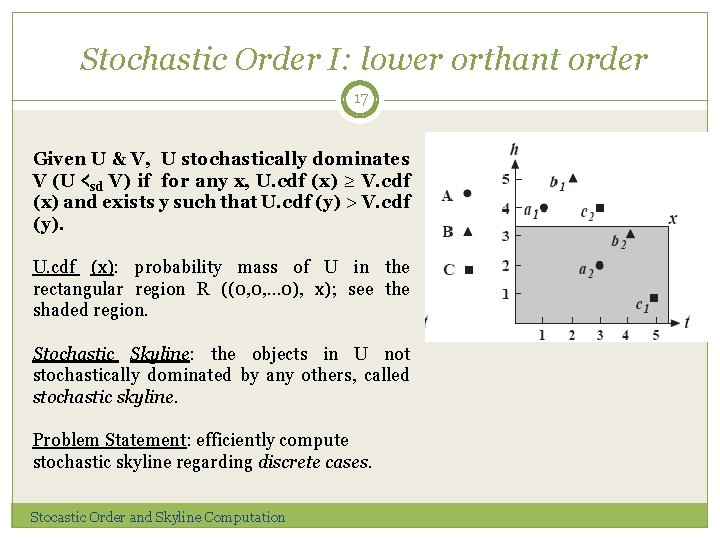
Stochastic Order I: lower orthant order 17 Given U & V, U stochastically dominates V (U ≺sd V) if for any x, U. cdf (x) ≥ V. cdf (x) and exists y such that U. cdf (y) > V. cdf (y). U. cdf (x): probability mass of U in the rectangular region R ((0, 0, … 0), x); see the shaded region. Stochastic Skyline: the objects in U not stochastically dominated by any others, called stochastic skyline. Problem Statement: efficiently compute stochastic skyline regarding discrete cases. Stocastic Order and Skyline Computation

Minimality of stochastic skyline 18 Stochastic skyline removes all objects not preferred by any non-negative decreasing functions! Stocastic Order and Skyline Computation

Testing if U ≺sd V 19 Violation point: a point x in Rd+ is a violation point regarding U ≺sd V if U. cdf (x) < V. cdf (x). Testing algorithm: if no violation points, then U ≺sd V. Not enough to test instances. Stocastic Order and Skyline Computation

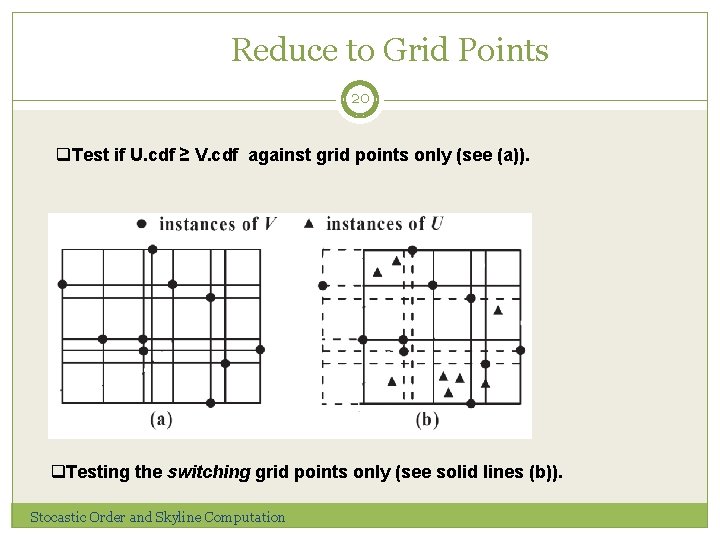
Reduce to Grid Points 20 q. Test if U. cdf ≥ V. cdf against grid points only (see (a)). q. Testing the switching grid points only (see solid lines (b)). Stocastic Order and Skyline Computation

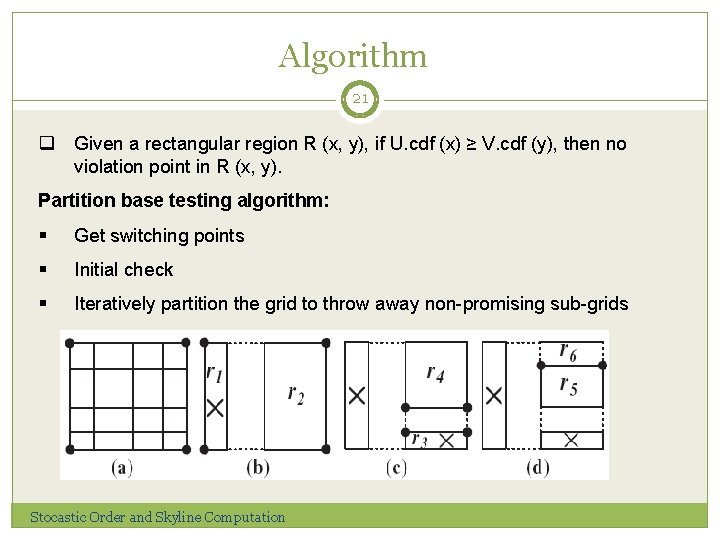
Algorithm 21 q Given a rectangular region R (x, y), if U. cdf (x) ≥ V. cdf (y), then no violation point in R (x, y). Partition base testing algorithm: § Get switching points § Initial check § Iteratively partition the grid to throw away non-promising sub-grids Stocastic Order and Skyline Computation

Complexity 22 q. The algorithm runs O (dm log m + md (T (Uartree) + T (Vartree))) where m is the number of instances in V. q. NP-Complete regarding d. Covert (the decision version of) the minimal set cover problem to a special case of the testing problem. Stocastic Order and Skyline Computation

Usual Order 23 Lower orthant order helps retrieve minimum candidate sets for monotonic multiplication functions. How about more general monotonic functions, like linear functions ?

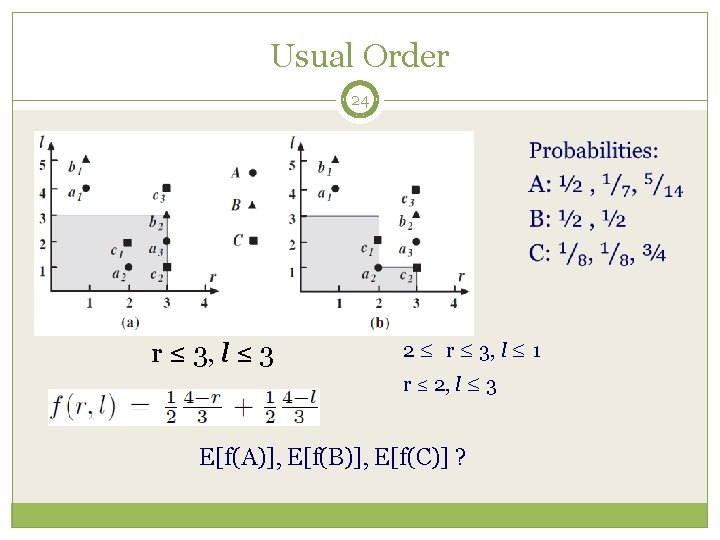
Usual Order 24 r ≤ 3, l ≤ 3 2 ≤ r ≤ 3, l ≤ 1 r ≤ 2, l ≤ 3 E[f(A)], E[f(B)], E[f(C)] ?

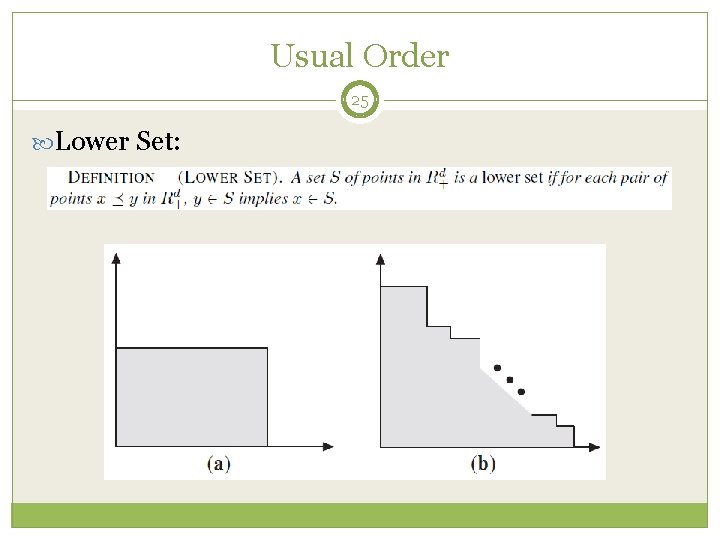
Usual Order 25 Lower Set:

Usual Order 26

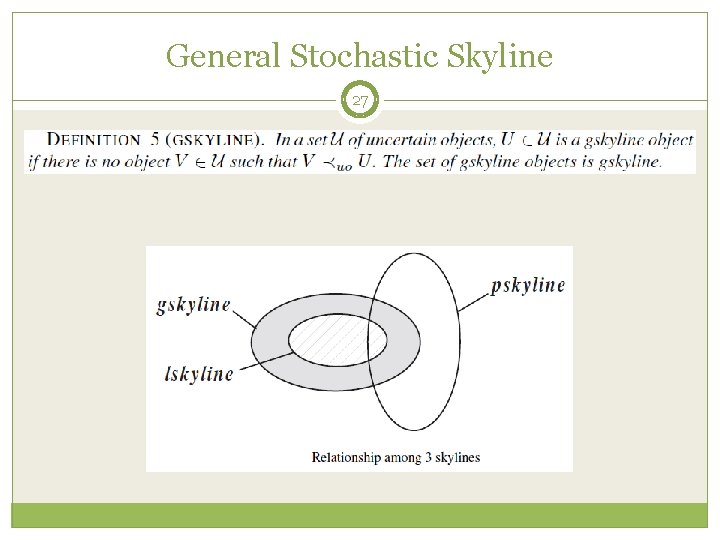
General Stochastic Skyline 27

Verification Algorithm 28 Verification: to determine if U ≺uo V Naively: test U. cdf(S) ≥ V. cdf(S) against every lower set S (infinite number of lower sets) From infinite to finite: (all subsets of V still exponential)

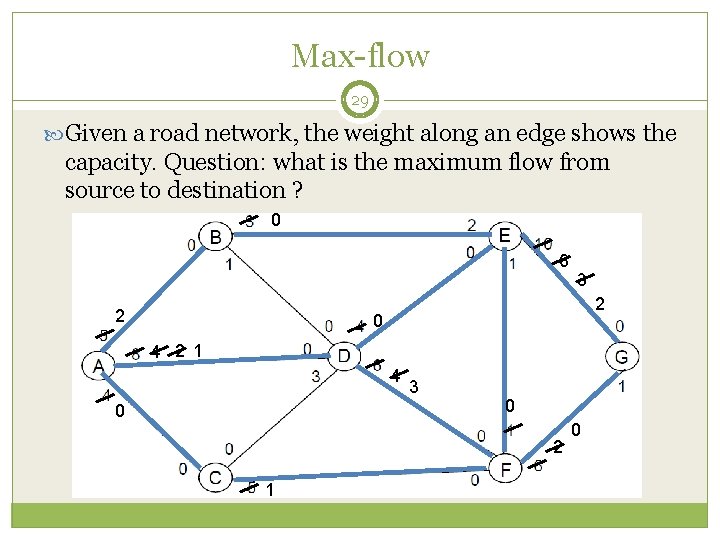
Max-flow 29 Given a road network, the weight along an edge shows the capacity. Question: what is the maximum flow from source to destination ? 0 6 2 3 2 0 4 2 1 4 0 3 0 2 1 0

Max flow 30 Max-flow / min-cut Theorem: for any network having a single source and a single destination node, the maximum flow from origin to destination equals the minimum cut value for all cuts in the network. Ford and Fulkerson algorithm

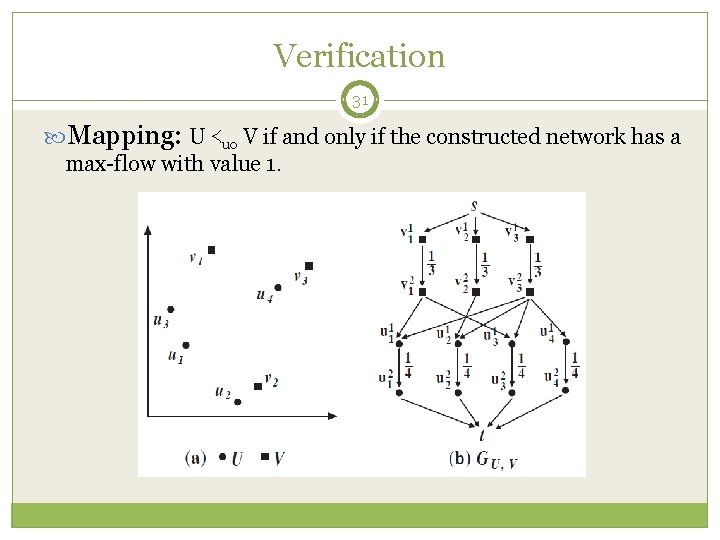
Verification 31 Mapping: U ≺uo V if and only if the constructed network has a max-flow with value 1.

Verification 32 Time Complexity: O(t. G + mnlogm) t. G : time to construct GU, V m: number of arcs n: number of nodes Stocastic Order and Skyline Computation

Verification 33 Compression: R-tree based level-by-level dominance checking Stocastic Order and Skyline Computation

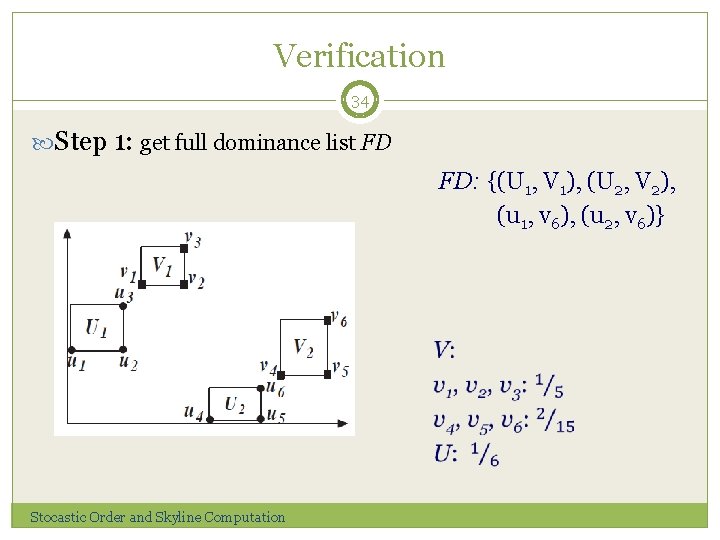
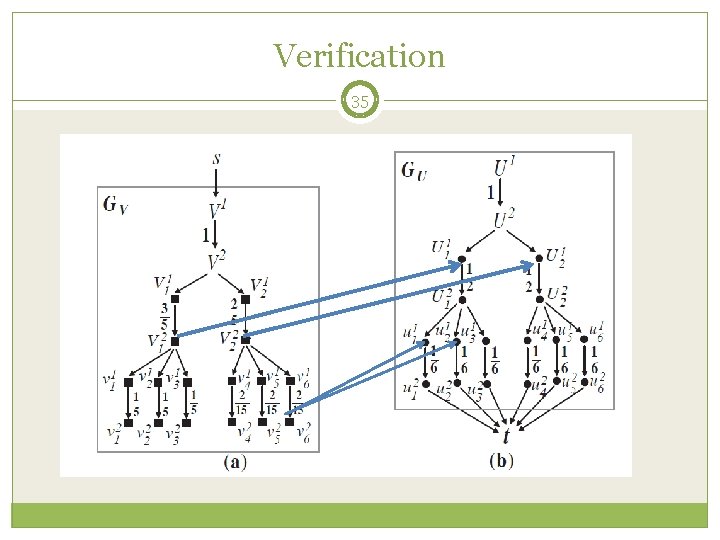
Verification 34 Step 1: get full dominance list FD FD: {(U 1, V 1), (U 2, V 2), (u 1, v 6), (u 2, v 6)} Stocastic Order and Skyline Computation

Verification 35

Framework 36 U ≺uo V (U ≺lo V) preserves the transitivity: ≺uo W if U ≺uo V, V could be removed since for any W s. t. V ≺uo W, U Apply standard filtering paradigm Stocastic Order and Skyline Computation

Framework 37 BBS Algorithm: access the entries based on the minimum distance to the origin [SIGMOD 03]

Framework 38 Index: a global R-tree, indexing the MBB of all objects Progressive: iteratively traverse the global R-tree to find the data entry with smallest distance from lower corner to origin Only need to check U ≺uo Stocastic Order and Skyline Computation V or V ≺uo U, but not both

Filtering 39 Pruning Rule 1: throw away fully dominated entries

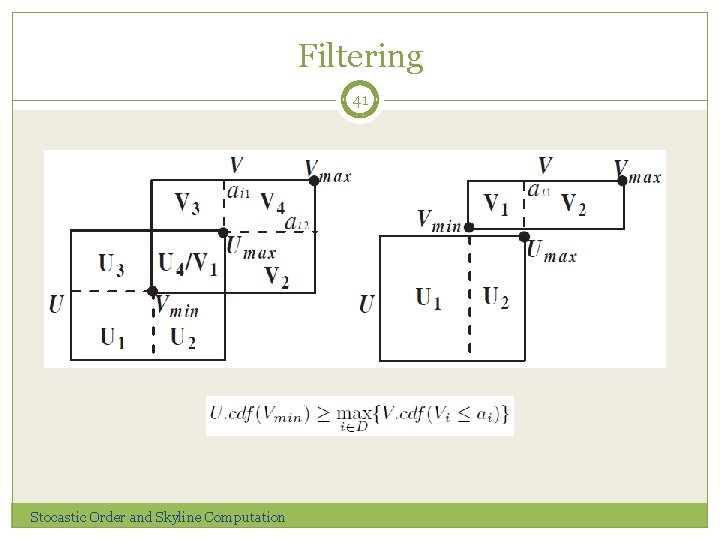
Filtering 40 Pruning for lskyline: let R(x, y) denote a rectangular region in d-dimensional space where the lower and upper corners are x and y, respectively. Stocastic Order and Skyline Computation

Filtering 41 Stocastic Order and Skyline Computation

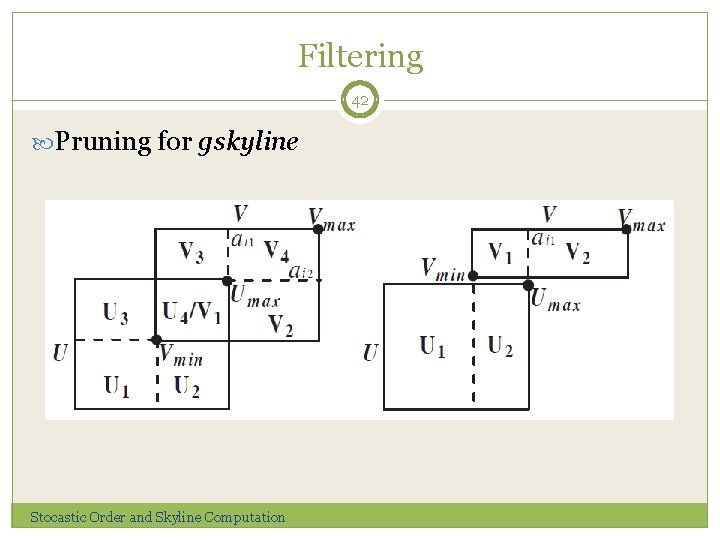
Filtering 42 Pruning for gskyline Stocastic Order and Skyline Computation

Filtering 43 Statistic based Pruning: mean of intermediate entry E: the minimum among all its children variance of intermediate entry E: the maximum among all its children Stocastic Order and Skyline Computation

Size Estimation: 44 Expected size: size of stochastic skyline in Rd is bounded by that of conventional skyline in Rd+1; i. e. , lnd (n)/(d+1)! Stocastic Order and Skyline Computation

Stochastic Order is a Better Model 45 a novel skyline operator: stochastic skyline guarantee minimality. NP-complete to test stochastic order (lower orthant order). PTIME to test general order though it is more complex regarding geometric form. novel efficient algorithms to compute stochastic order. Stocastic Order and Skyline Computation

46