STATISZTIKUS TERMODINAMIKA ALKALMAZSOK P W Atkins Fizikai kmia

STATISZTIKUS TERMODINAMIKA: ALKALMAZÁSOK • P. W. Atkins: Fizikai kémia II. - Szerkezet (Tankönyvkiadó, Budapest, 2002), 20. fejezet • Keszei Ernő: Bevezetés a kémiai termodinamikába (ELTE egyetemi jegyzet, 2007), 10. fejezet

Statisztikus termodinamika: alkalmazások • A termodinamikát, spektroszkópiát és kvantummechanikát összekötő híd az állapotösszeg. Ha ezt ismerjük, akkor • a különféle termodinamikai függvényeket, • a hőkapacitást, • az entrópiát, • az egyensúlyi állandót meghatározhatjuk. • Feladatok: • Termodinamikai függvények meghatározása az állapotösszegből. • Állapotösszeg meghatározása spektroszkópiai adatokból. q

Termodinamikai függvények (4. előadás) • Belső energia: • Entrópia: • Független részecskék tárgyalásakor q és Q között összefüggés van: Megkülönböztethető Megkülönböztethetetlen részecskék • Minden további termodinamikai függvény is kapcsolatban van U-val vagy S-sel, így ezek alakja is meghatározható.

Termodinamikai függvények TD Levezetés Kanonikus függvény alapja állapotösszeggel kifejezve Előző (4. ) előadás Független, megkülönböztethetetlen Független, megkülönböztethető

Állapotösszeg • Adott molekula energiája a különböző mozgásfajtákból származó energiák összege: ahol T a haladó mozgást (transzlációt), R a forgást (rotációt), V a rezgést (vibrációt), E az elektronoktól származó hozzájárulást jelöli. • Mivel az egyes mozgásfajták (a T kivételével) nem teljesen függetlenek egymástól, ez az elkülönítés csak közelítő jellegű. • Az állapotösszeg ez alapján szintén tényezőkre bontható: • Ez azt jelenti, hogy az egyes hozzájárulásokat külön-külön vizsgálhatjuk meg.

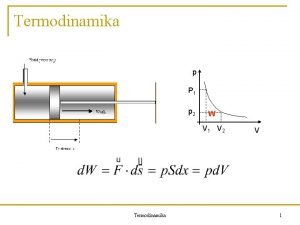
Állapotösszeg a) A haladó mozgás hozzájárulása • A V tértfogatú edénybe zárt, m tömegű részecske haladó mozgásának állapotösszege (4. előadás): és • T → ∞ esetében q. T → ∞, mert végtelen sok állapot válik elérhetővé.

Állapotösszeg b) A forgási hozzájárulás • Aszimmetrikus lineáris molekulák forgására (pl. HCl): és Lineáris molekulák forgási energiaszintjei. Mindegyik J szinthez 2 J + 1 degenerált állapot tartozik. ahol B a forgási álladó, J az impulzusmomentum nagysága. • A q. R mennyiséget közvetlenül úgy adhatjuk meg, hogy a kísérletileg meghatározott E(J) energiaszinteket az egyenletbe helyettesítjük és a sort numerikusan összegezzük.

Állapotösszeg b) A forgási hozzájárulás • Aszimmetrikus lineáris molekulák forgására (pl. HCl): és Lineáris molekulák forgási energiaszintjei. Mindegyik J szinthez 2 J + 1 degenerált állapot tartozik. ahol B a forgási álladó, J az impulzusmomentum nagysága. • Szobahőmérsékleten k. T/hc ≈ 200 cm– 1. A molekulák jó részénél sok forgási energiaszint van betöltve, mert a forgási állandó kis érték: B/cm– 1 CO 2 I 2 HI HCl (H 2) 0, 39 0, 037 6, 5 10, 6 (60, 9) • Ilyen esetekben az összegzés integrálással helyettesíthető:

Állapotösszeg b) A forgási hozzájárulás • Aszimmetrikus lineáris molekulák forgására: • Szimmetrikus lineáris molekulákra (mivel a 180°-os elforgatás eredményeként a molekula az eredetitől megkülönböztethetetlen állapotba kerül: ahol σ a szimmetriaszám (a vizsgált molekula meg nem különböztethető orientációinak a száma).

Állapotösszeg b) A forgási hozzájárulás • Az A, B, C forgási állandókkal bíró nemlineáris molekuláknál: • Általános képlet nemlineáris molekuláknál: ahol σ a szimmetriaszám (a vizsgált molekula meg nem különböztethető orientációinak a száma). σ CO 2 C 2 H 2 O NH 3 CH 4 C 6 H 6 2 2 2 3 12 12

Állapotösszeg c) A rezgési hozzájárulás • Egy molekula rezgési állapotösszegének a meghatározásához a definícióban szereplő exponenciális függvényekbe be kell írni a mért rezgési energiaszinteket, majd numerikusan összegezni. • Ha a többatomos molekula anharmonicitása kicsiny, akkor a normálrezgések egymástól függetlenek, és minden rezgésnek saját állapotösszege van. A teljes rezgési állapotösszeg az egyedi állapotösszegek szorzata: ahol q. V(K) a K-adik normálrezgés állapotösszege, melyet a megfigyelt spektroszkópiai energiaszintek közvetlen összegzésével határozhatunk meg.

Állapotösszeg c) A rezgési hozzájárulás • Nem túl nagy rezgési gerjesztettségnél használhatjuk a harmonikus közelítést, így a rezgési energiaszintek: ahol 0, 1, 2, … • Ha az energiát a zérusponti energiától mérjük, akkor a • Többatomos molekuláknál mindegyik normálrezgésnek ilyen alakú állapotösszege van. adja meg. Az állapotösszeg: Potenciális energia lehetséges értékeket Harmonikus oszcillátor Anharmonikus oszcillátor Kötéstávolság

Állapotösszeg c) A rezgési hozzájárulás • Sok molekulában a rezgési hullámhossz olyan nagy, hogy βhc > 1. Ezekben az esetekben: Ez azt jelenti, hogy csak a zérusponti energiaszint van számottevően betöltve. • k. T >> hc esetén (azaz magas hőmérsékleten): A sorfejtés érvényességére vonatkozó hőmérsékleti határ: ahol ΘV a rezgési karakterisztikus hőmérséklet. A magas hőmérséklet azt jelenti, hogy T >> ΘV. I 2 F 2 HCl H 2 215 892 2990 4400 309 1280 4300 6330

Állapotösszeg d) Az elektronok hozzájárulása • A gerjesztett elektronállapotok energiái általában messze vannak az alapállapotétól, ezért általában q. E = 1. • Fontos kivétel, amikor az atom vagy molekula elektronburkának alapállapota degenerált és q. E = g. E (a degeneráció foka). Az alkálifém-atomok alapállapotának degenerációja (az elektron kétféle orientációjának megfelelően) 2.

Állapotösszeg d) Az elektronok hozzájárulása • Bizonyos atomoknak és molekuláknak vannak kis energiájú gerjesztett állapotaik. L: pályaimpulzus-momentum S: spinmomentum • A kétszeresen degenerált, alacsonyabb energiájú term betöltési száma nagyobb. • Az elektronhoz rendelhető állapotösszeg: • T = 0 esetén q. E = 2, mert csak az alapállapot elérhető. • 25 °C-on q. E = 3, 1. • Nagyobb hőmérsékleten q. E → 4. NO molekula konfiguráció: [N 2]π1

Állapotösszeg e) A teljes állapotösszeg • A teljes állapotösszeg az egyes hozzájárulások szorzata. Kétatomos molekulák esetén pl. : • Az így nyert teljes állapotösszegek közelítő jellegűek, mert tartalmazzák azt a feltevést, hogy o a forgási szintek egymáshoz közel vannak, o a regzési szintek harmonikusak • A közelítés elkerülhető, ha az egyes összegeket közvetlenül spektroszkópiai adatokból határozzuk meg.

Statisztikus termodinamika alkalmazása • A molekulák energiaszintjeinek az ismeretében most már képesek vagyunk arra, hogy bármelyik termodinamikai mennyiséget meghatározzuk. • Négy mennyiség esetében részletesen megnézzük, hogyan is kell elvégezni a számolást: • Átlagos energia • Hőkapacitás • Zéruspont-entrópia • Egyensúlyi állandó q

Statisztikus termodinamika alkalmazása a) Átlagos energia • A különféle mozgásfajták átlagos energiájának ismerete általában hasznos. • Ha az állapotösszeget sikerült az egyes mozgásfajtákhoz tartozó hozzájárulásokra bontanunk, akkor: • Mivel a belső energia az egyes mozgásfajták átlagos energiája, így: ahol és M = T, R, V és E.

Statisztikus termodinamika alkalmazása a) Átlagos energia – haladó mozgás • Vizsgáljuk meg az X hosszúságú 1 D rendszert, melyre q. T = X/Λ. Ekkor: és • 3 D esetében: • Ez egyezésben van a klasszikus ekvipartíciós tétellel, tehát hogy minden négyzetes tag -vel járul hozzá a teljes energiához, az átlagos energia pedig független az edény méretétől. Ennek a TD megfelelője az, hogy a tökéletes gáz belső energiája független a térfogattól.

Statisztikus termodinamika alkalmazása a) Átlagos energia – forgás • A lineáris molekulák átlagos forgási energiája: • Alacsony hőmérsékleten: • Magas hőmérsékleten: • Ez ismét összhangban van az ekvipartíciós tétellel, mivel egy lineáris molekula 2 tengely körül tud forogni.

Statisztikus termodinamika alkalmazása a) Átlagos energia – rezgés • A rezgési állapotösszeget a következő egyenlet adja meg: • Mivel q. V független a térfogattól, így: és • Ha a rezgés zérusponti energiája is lényeges, akkor a jobb oldalhoz energiát kell hozzáadni. • Magas hőmérsékleten: és • Ekvipartíció: a rezgési energia egy 1 D mozgási és egy helyzeti tag összege, ezért a szabadsági fok 2.

Statisztikus termodinamika alkalmazása b) Hőkapacitás • Az állandó térfogathoz tartozó hőkapacitás: • Ugyanakkor: • Mivel a tökéletes gáz belső energiája különböző hozzájárulások összege, így a hőkapacitás is: • Az egyes mozgásfajták hozzájárulása:

Statisztikus termodinamika alkalmazása b) Hőkapacitás – egyedi hozzájárulások • Transzlációs járulék gázokban (ha a hőmérséklet nagy, azaz meghaladja a kondenzációs hőmérsékletet): • Egyatomos gáznál csak haladó mozgás lehetséges: a He mólhője valóban ennyi igen széles hőmérséklettartományban (kb. 2000 K). • Tökéletes gázra: • ezért egyatomos tökéletes gázra: és

Statisztikus termodinamika alkalmazása b) Hőkapacitás – egyedi hozzájárulások • Ha a hőmérséklet elegendően nagy ahhoz, hogy a lineáris molekula forgása jelentősen gerjesztődjön, akkor: • Nemlineáris molekulákra: • Nagyon kis hőmérsékleten csak a legalacsonyabban fekvő forgási állapot van betöltve, és a forgás nem járul hozzá a hőkapacitáshoz:

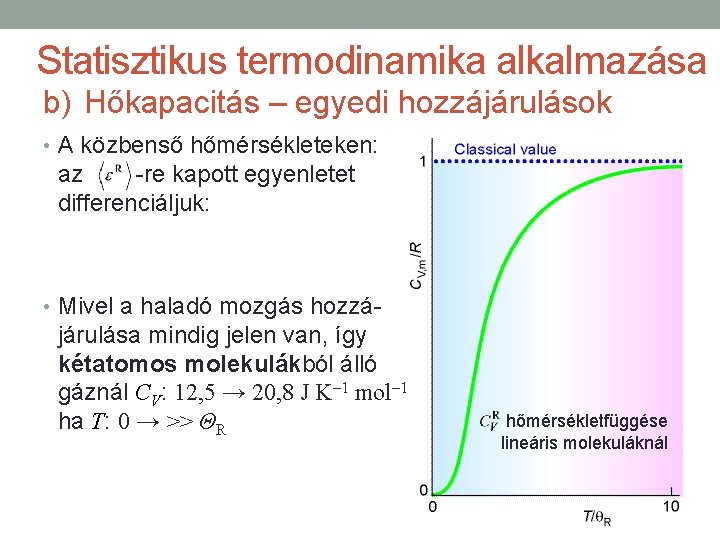
Statisztikus termodinamika alkalmazása b) Hőkapacitás – egyedi hozzájárulások • A közbenső hőmérsékleteken: az -re kapott egyenletet differenciáljuk: • Mivel a haladó mozgás hozzá- járulása mindig jelen van, így kétatomos molekulákból álló gáznál CV: 12, 5 → 20, 8 J K– 1 mol– 1 ha T: 0 → >> ΘR hőmérsékletfüggése lineáris molekuláknál

Statisztikus termodinamika alkalmazása b) Hőkapacitás – egyedi hozzájárulások • A molekularezgések csak akkor járulnak hozzá a hőkapacitáshoz, ha a hőmérséklet elég magas ahhoz, hogy számottevően gerjessze azokat. • Az ekvipartíciónak megfelelő átlagos energia modusonként k. T, így egy modus maximálisan R-rel járul hozzá a moláris hőkapacitáshoz. • Nagyon szokatlan az olyan eset, amikor a rezgések gerjesztési foka az ekvipartíció tételének érvényességéhez elegendő. Helyesebb a teljes formulát használni:

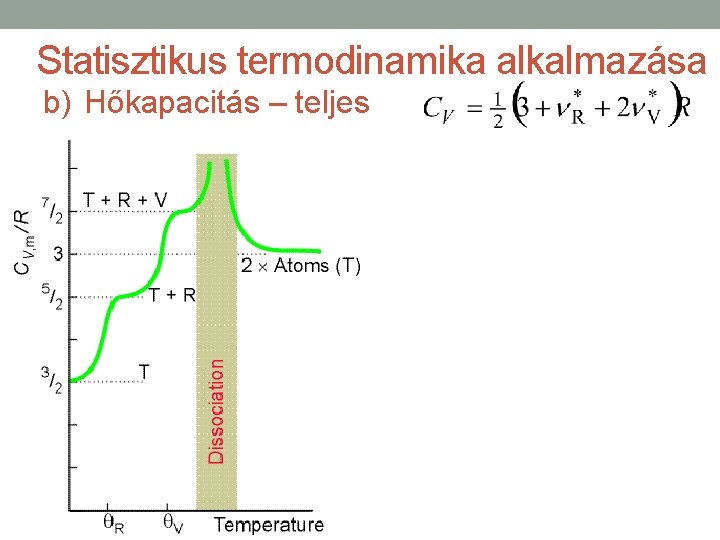
Statisztikus termodinamika alkalmazása b) Hőkapacitás – teljes • A teljes hőkapacitást minden hozzájárulásra kiterjedő összegzéssel kapjuk. • Ha az ekvipartíció tétele érvényes, akkor a hőkapacitást az aktív modusok figyelembe vételével határozhatjuk meg. • Gázokban mindig aktív mindhárom transzlációs modus ( ). • Ha az aktív forgási modusok száma , akkor a forgási hozzájárulás. Szokásos hőmérsékleteken egyatomos gázokra , lineáris molekulákra , nemlineáris molekulákra. • Ha a hőmérséklet elegendően magas, akkor számú rezgési modus is aktívvá válik, és a rezgési hozzájárulás értéke. A legtöbb esetben.

Statisztikus termodinamika alkalmazása b) Hőkapacitás – teljes

Statisztikus termodinamika alkalmazása c) Zéruspont-entrópia • Az entrópia értéke kiszámolható spektroszkópiai adatokból, de más kísérletekből is meghatározható. • Sok esetben jó egyezést tapasztalunk, néha azonban a spektroszkópiai adatokból számolt S nagyobb. Ennek oka: • nem vettünk figyelembe valamilyen fázisátmenetet, • még 0 K-en is van bizonyos mérvű rendezetlenség. • A 0 K-en meglévő entrópiát zéruspont-entrópiának vagy maradékentrópiának nevezzük. • Kristályban két különböző lehetséges orientáció. • N db. CO molekula esetén 2 N db. elrendeződés.

Statisztikus termodinamika alkalmazása c) Zéruspont-entrópia • Az entrópia értéke kiszámolható spektroszkópiai adatokból, de más kísérletekből is meghatározható. • Sok esetben jó egyezést tapasztalunk, néha azonban a spektroszkópiai adatokból számolt S nagyobb. Ennek oka: • nem vettünk figyelembe valamilyen fázisátmenetet, • még 0 K-en is van bizonyos mérvű rendezetlenség. • A 0 K-en meglévő entrópiát zéruspont-entrópiának vagy maradékentrópiának nevezzük. • Kristályban egy O-t négy H vesz körül, 2 kovalens, 2 hidrogénkötéssel.

Statisztikus termodinamika alkalmazása d) Egyensúlyi állandó • A független molekulákból álló rendszer szabadentalpiája: • A standard-szabadentalpia és az egyensúlyi állandó (Kp) kapcsolata: • Az egyensúlyi állandó meghatározásánál ezt a két egyenletet kell kombinálni. • Az egyes komponensek standard moláris szabadentalpiájára van szükségünk. Ehhez ismerni kell a moláris állapotösszeget po = 1 bar nyomáson ( ). Mivel csak a transzlációs állapotösszeg függ a nyomástól:

Statisztikus termodinamika alkalmazása d) Egyensúlyi állandó • Vizsgáljuk a következő reakciót: • A reakció standard moláris szabadentalpiája: • Tökéletes gáznál G(0) = U(0), így: • ΔUo(0) a reaktánsok és termékek sztöchiometriai együtthatókkal súlyozott moláris zérusponti energiájának a különbsége, amire rendszerint a ΔE 0 jelölést használjuk, így: • Tehát:

Statisztikus termodinamika alkalmazása d) Egyensúlyi állandó • Tehát a kapcsolat az egyensúlyi állandó és az állapotösszeg között:

Statisztikus termodinamika alkalmazása d) Egyensúlyi állandó • Tehát a kapcsolat az egyensúlyi állandó és az állapotösszeg között: 2 • A direkt reakció: • Az egyensúlyi állandó: • Az állapotösszeg bevezetésével: ahol ΔE 0 = 2 U(X) – U(X 2) = D(X 2) (a molekula disszociációs energiája).

Statisztikus termodinamika alkalmazása d) Egyensúlyi állandó • Tehát a kapcsolat az egyensúlyi állandó és az állapotösszeg között: 2 • Az atomok moláris állapotösszege csak a haladó mozgástól és az elektronállapotok degenerációjától függ, tehát: ahol • Kétatomos molekuláknál már forgás és rezgés is van, így: