A fizika feladatok szerepe a tantsban Ksztette Dr

A fizika feladatok szerepe a tanításban Készítette: Dr. Varga Klára

„ Megfigyelés, kísérlet, mérés és számolás nélkül nincs természetkutató munka, nem születik tudás” ( Leonardo da Vinci )

A fizika feladatok n Fizikai feladatnak nevezünk minden olyan problémát, amelynek megoldása fizikai jelenségek vagy mennyiségek közötti összefüggések felhasználását teszik szükségessé. n A fizikai feladatok szerepe és feladata: n a. segítségükkel világosabbak, pontosabbak, alkalmazhatóbbak lesznek a fizikai fogalmak, b. a gondolkodóképesség, az önálló gondolkodás fejlesztését nagyban segítik, c. az ismeretek összefüggésekben való látását kívánják meg, d. alkalmazásukkal eldönthető, a tudás mellett érti-e, képes-e ismereteit alkalmazni a tanuló, képes-e önálló, alkotó munkára,

A fizika feladatok n A fizika feladatok szerepe és feladatai: e. a fizika különböző fejezetei közötti összefüggések felhasználását igénylik, f. az ismeretek rögzítésének, erősítésének, megszilárdításának fontos eszköze, g. a mindennapokhoz, az élethez viszik közel a fizikát, h. alkalmasak a tanulók fizikai ismereteinek bővítésére, i. mindezek a tulajdonságok alkalmassá teszik a tantervi ismeretek, jártasságok elsajátításának

Feladattípusok n A válaszadás módja szerint: n 1. feleletválasztásos feladatok (zárt kérdések): a feladatok után általában 3 -6 alternatív válasz szerepel. Megoldása során a felsorolt lehetőségek közül a helyes választ kell megjelölni. Fajtái: a. egyszerű választás ( több válasz közül egy helyes, több helyes vagy hibás válasz kiválasztása), b. többszörös választás (több válasz közül egy vagy kettő, vagy három, vagy mind az összes helyes), c. alternatív választás ( n

Feladattípusok A válaszadás módja szerint 1. Feleletválasztásos feladatok Fajtái: d. válaszok illesztése ( egy az egyhez, többszörös hozzárendelés, párosítás) e. relációanalízis ( A megoldás során a tanulónak ki kell választani a megfelelő választ az összes lehetséges válaszvariáció közül)

Feladattípusok n n 2. feleletalkotásos feladatok esetén a válaszadónak önállóan kell megfogalmazni a választ, megoldani a feladatot. A feleletalkotásos feladatokkal a tudás többféle összetevőit lehet tesztelni, de javításuk, kódolásuk általában több figyelmet igényel. Fajtái: - kiegészítés (mondatok, állítások kiegészítése), - rövid válasz (szavak, számok megadása), - hosszú válasz (hosszabb kifejezések, egész mondat) - esszé típusú feladatok ( több mondatból álló

Feladatok és azok megoldása a tanítási órákon n A feladatok megoldása hatékony módszer a tanulók képességeinek fejlesztéséhez, a tananyag eredményes feldolgozásához. Feladatmegoldásnak tekinthetünk minden olyan általunk kijelölt tevékenységet, amelyet a tanulók önállóan, párban, vagy csoportban végeznek. Ilyen értelemben megkülönböztethetünk iskolai – és házi feladatot; a tevékenység jellegét tekintve szóbeli, írásbeli, rajzos vagy gyakorlati feladatot. A feladatok lehetnek számításos és nem számításos feladatok.

Feladatok és azok megoldása a tanítási órákon n A tanítás - tanulás folyamatában betöltött szerepüktől függően általában az ismeretek rögzítését vagy alkalmazását szolgálhatják a feladatmegoldások. A feladatmegoldás csak akkor fejlesztő hatású, ha a tanulók rendelkeznek a feladatok megoldásához szükséges ismeretekkel, készségekkel, képességekkel; értik a feladatokban rejlő kérdést, problémát; ismerik a helyes megoldás módszerét, technikáját. E feltételeknek a tanulók különböző mértékben tudnak megfelelni, ezért célszerű a feladatok differenciálása.

Feladatok és azok megoldása a tanítási órákon n A feladatok az ismeretek felidézését, rendszerezését és gyakorlását szolgálják. Lehetőséget adnak a felkészültség ellenőrzésére és a önellenőrzésre is. Az általunk megalkotott feladatoknak illeszkedni kell a tantervhez, a tanterv által előírt ismeretanyagot kell feldolgoznunk. Úgy kell összeválogatni a feladatokat, hogy azok motiválók, ösztönzők, érdeklődést-felkeltők legyenek. Egy-egy feladat megoldása után beszéljük meg a helyes megoldást, elemezzük a kapott eredményeket.

Feladatok és azok megoldása a tanítási órákon n n A feladatok összeállításánál követelmény a fokozatosság elvének betartása. A feladatok szövege világos, egyértelmű legyen, a benne szereplő adatok reálisak legyenek. A feladatok megoldásához elengedhetetlen a megfelelő fizikai tények, jelenségek, összefüggések, törvények pontos ismerete, azok alkalmazása. Szükséges a feladatmegoldás egymást követő lépéseinek, menetének alkalmazása és a gondolkodás.

A feladatmegoldás lépései: n n n n 1. A feladat szövegének elolvasása és megértése, 2. az ismert mennyiségek kigyűjtése, az ismeretlen mennyiség és mértékegységének felírása, 3. a. a használni kívánt összefüggés felírása, b. a feladat logikai úton történő megoldása, 4. behelyettesítés a mértékegységekkel együtt, 5. számítás elvégzése, 6. a kapott eredmény elemzése, 7. válaszadás a kérdésre.

Rejtvény típusú feladatok n Ide tartozhatnak a betűrejtvények, képrejtvények, szókereső típusú rejtvények, szóösszeállító feladatok, keresztrejtvények. A fizika feladatok nem egyszerű rejtvények, nem is játékok, mögöttük a természet törvényei, a természet jelenségei vannak. De ezért, vagy éppen ezért lehetnek szórakoztatók is. A rejtvényekkel is lehet motiválni, érdeklődést felkelteni. A rejtvényfejtés során a megértés szintjét kell elérni.

Rejtvény típusú feladatok n Nem elég ráismerni az adott jelenségre, fogalomra, illetve az azt jelölő szóra, névre, hanem a tanulóknak kell kimondani, leírni a jelenség nevét. Az egyszerűbb rejtvényeket egyéb kérdésekkel, feladatokkal is ki lehet egészíteni, ezáltal azok egészen összetett feladatokká válhatnak. Ezeket a feladatokat is megoldhatják a tanulók önállóan, párban, csoportban is, illetve frontális osztálymunkában.

Rejtvények n 1. Rakja jó sorrendbe a betűket, és egy – egy természettudós nevét kapja. Kiről van szó? ZUMLKSBUO MEEVNGEJELY PSZIATRAGO n Megfejtés: n KOLUMBUSZ MENGYELEJEV PITAGORASZ n n n

Rejtvények n Fejtse meg a rejtvényt! n a. TAZROBMOD n b. MÁKFELFORSZÍN n c. ÁRVÍOZÓZT n d. NYKÁIVNSCÁS n e. BTMEOTDŐ

Rejtvények n Megoldások: n a. DOMBORZAT n b. FELSZÍNFORMÁK n c. VÍZTÁROZÓ n d. ÁSVÁNYKINCS n e. DOMBTETŐ

Rejtvények Rakja helyes sorrendbe a betűket és testneveléssel kapcsolatos szavakat kap. Melyek ezek? n a. ÁLLZENLÁSKÉ n b. PLDARÖAB n c. ÁTGUFORLÓDURULÁS n d. YÚTÓNJ n

Rejtvények n Megfejtés: a. KÉZENÁLLÁS n b. RÖPLABDA n c. GURULÓÁTFORDULÁS n d. NYÚJTÓ n

Rejtvények n Keressen legalább 4 testneveléssel kapcsolatos szót a táblázatban a betűk helyes összeolvasásával! L S Z A L B A X K A U T B O G Z Á N D P O G Y S A

Rejtvények n MEGFEJTÉS: LABDA n BUZOGÁNY n SZALAG n

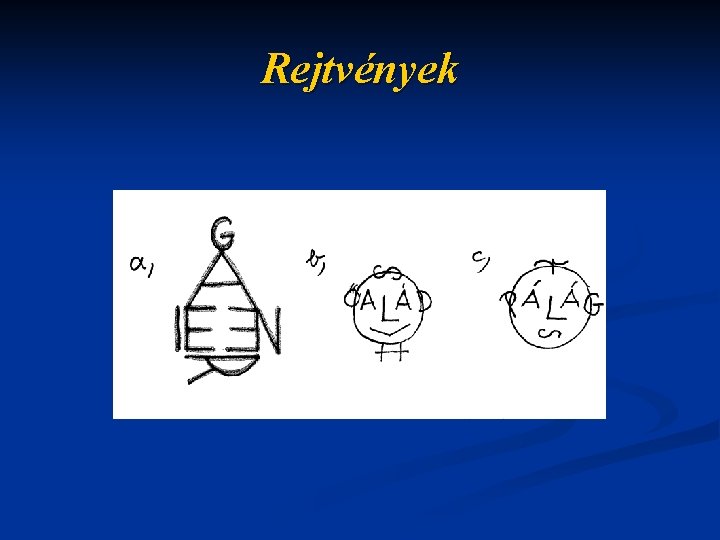
Rejtvények

Rejtvények n Megfejtések: a. E N E R G I A b. O L V A D Á S H Ő n c. P Á R O L G Á S n n

Rejtvények n Fejtse meg a képrejtvényeket!

Rejtvények n Megfejtések: n a. G Ő Z G É P b. F A J H Ő c. H Ő Á R A M L Á S n n

Rejtvények Keressen a betűhalmazban legalább 4 db fizikával kapcsolatos fogalmat! M Á Z S G É S E T N U L M E E S Ó Ö R S K P T

Rejtvények n Megfejtés: T Ö M E G S Z Á M, n T Ö M E G, n M É T E R, n ÉGÉS, n M Á G N E S, n PÓLUS n

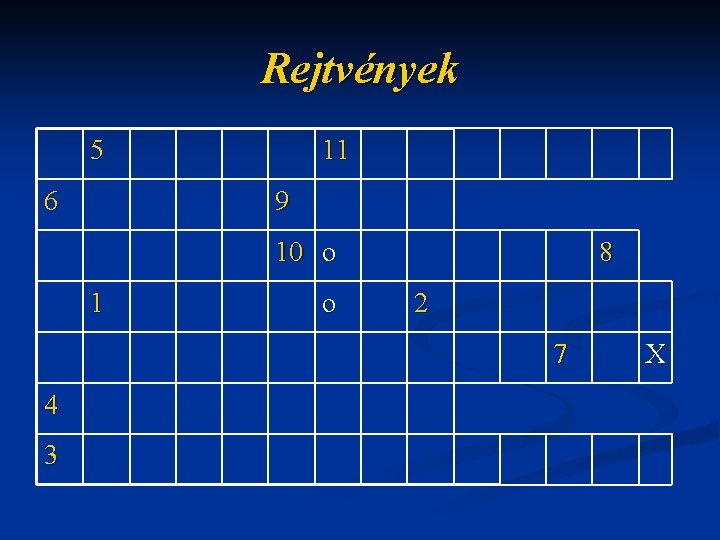
Rejtvények 5 6 11 9 10 o 1 o 8 2 7 4 3 X

Rejtvények 1. A folyadék súlyából származó nyomás a …nyomás n 2. Nyomást mérünk vele n 3. A felületi feszültséggel is foglalkozott n 4. Magyar űrhajós n 5. A tömeg a testek ……. . mértéke n 6. A hőterjedés egyik formája n 7. A testek mozgását akadályozhatja n

Rejtvények H I 5 D M A N 6 E Ö T F A 1 R T E R Z T 11 O M É9 T E A V L O R B Ö S 10 K A S H E H Ő Á 4 K Ö Z O S I K A Á N D 8 E R 2 T A L N S É7 G N Á L I R T E T L E R A M L Á S E G E L T L A N Á S

Rejtvények 12 1 9 14 4 2 6 11 7 13 5 8 3 10

Rejtvények n n n n n 1. Tükörről a fénysugarak……. . 2. 6*1023 db/mol=…. . szám 3. Az elemek helyét jelenti a periódusos rendszerben 4. Az anyag részecskéi között ható erő 5. A bolygók mozgását törvénybe foglalta 6. Nemesgáz 7. A gravitációval foglalkozott természettudós 8. A fizika egyik ága 9. A változó mozgásra jellemző mennyiség 10. Légköri fényjelenség

Rejtvények V A R K K H G M G S I V E O E É A E Y Z S O N H P L L C O I S G D É L I I H R V Z A S Z E U L A S Á A D Z I R M E N U R V R Á Ó E R Ő D N E O M S I I L V K Á Á A S N Y K

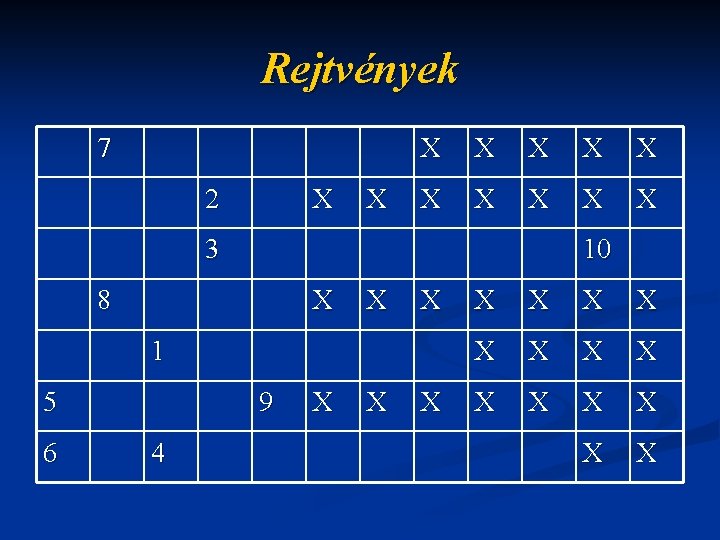
Rejtvények 7 2 X X X 3 10 8 X X X 1 5 6 9 4 X X X X X

Rejtvények Fejtse meg a rejtvényt! n 1. A térképen barnaszín jelöli. n 2. A Mátra legmagasabb pontja. n 3. A főfolyóba ömlenek. n 4. Megyénk legnagyobb folyója n 5. Budapest, hazánk ………. n 6. Az egyik égtáj n 7. Hazánk egyik szomszédos országa n

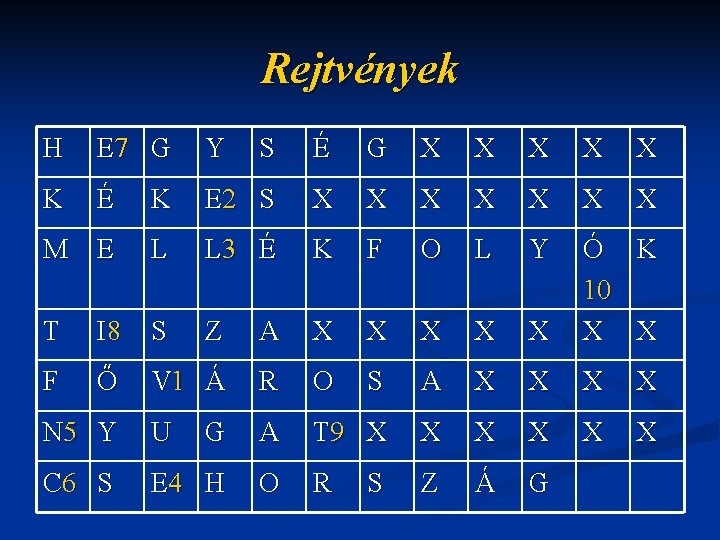
Rejtvények H E 7 G Y S É G X X X K É K E 2 S X X X X M E L L 3 É K F O L Y T I 8 S Z A X X X Ó K 10 X X F Ő V 1 Á R O S A X X N 5 Y U G A T 9 X X X C 6 S E 4 H O R Z Á G S

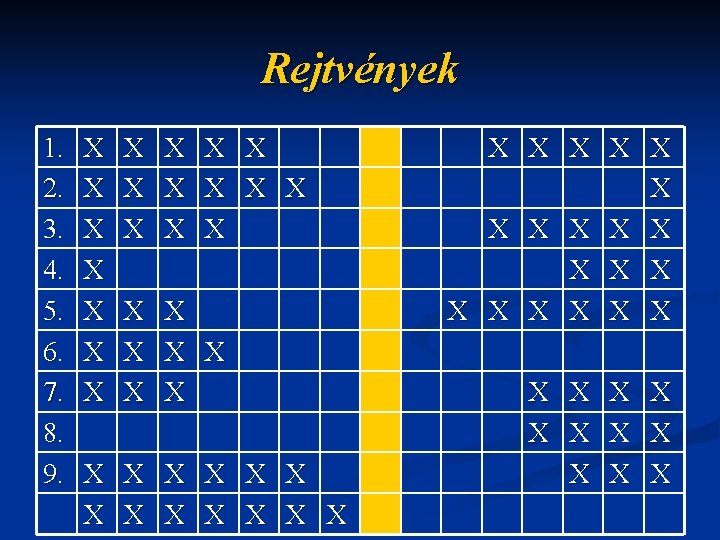
Rejtvények 1. 2. 3. 4. 5. 6. 7. 8. 9. X X X X X X X X X X X X X X X X X X

Rejtvények n n n n n 1. Az a vonal, amelyen a test mozgás közben végighalad. 2. Az egyik kölcsönhatás. 3. A nyomás mértékegysége. 4. Az a pont, ahol az erőhatás a testet éri. 5. Az erő hatásvonalának a forgástengelytől mért távolsága. 6. Az egyik halmazállapot. 7. Az az erő, amellyel az egyik test nyomja a másikat. 8. Görög természettudós, ő fedezte fel a felhajtóerő létezését. 9. Északi és déli pólusa van. 10. A mozgást jellemző egyik mennyiség.

Rejtvények 1. P Á L Y A 2. T E R M 3. P A S C A L 4. T Á M A D Á S P O 5. E R Ő K A R 6. C S E P P F 7. N Y O M Ó E R 8. A R K H I M É D É S 9. M Á G N S E B I K U S N T O Ő Z E E L Y Ó S S É G

Számításos fizika feladatok 1. Két helység közötti autóbuszjáraton a kocsik átlagsebessége az egyik irányban 40 km/h, a másik irányban 15 m/s. Mekkora az átlagsebesség a teljes fordulót figyelembe véve? 2. Az 1, 5 m/s 2 gyorsulással induló autó 8 s-ig halad egyenletesen gyorsuló mozgással, majd 20 s-ig egyenletesen mozog. Határozzuk meg az autó végsebességét és a megtett út nagyságát!

Számításos fizika feladatok-megoldása n 1. v 1 = 40 km/h v 2 = 15 m/s = 54 km/h s 1 = s 2 = s sö = 2 s vátl. = ? t 1 = s/v 1 t 2= s/v 2 tö = t 1 + t 2 tö = s(v 1 +v 2 )/v 1 v 2 vátl. = sö /tö vö = 2 s/s(v 1 +v 2 )/v 1 v 2 vátl. = 2 v 1 v 2 /(v 1 +v 2 ) vátl. = 46 km/h

Számításos fizika feladatok-megoldása n 2. t 1 = 8 s a = 1, 5 m/s 2 t 2 = 20 s tö = 28 s v=? sö = ? v(m/s) 8 t(s) 28 v = a·t 1 = 1, 5 m/s 2 · 8 s= 12 m/s sö = (tö +t 2 )·v/2 sö = (28+20) s·12 m/s/2 sö = 288 m

Számításos fizika feladatok 3. Egy játékautó lendkereke 6 cm átmérőjű. Mekkora a fordulatszáma, ha peremének pontjai 7, 2 km/h kerületi sebességgel mozognak? (10, 6 1/s) 4. A 150 kg tömegű motorkerékpár az indulás után mennyi idő múlva éri el a 36 km/h sebességet, ha a motor húzóereje 300 N? A veszteséget elhanyagoljuk. (5 s)

Számításos fizika feladatok-megoldása n 3. d = 6 cm = 0, 06 m vk = 7, 2 km/h = 2 m/s n=? vk = d·П·n n = vk /d·П n = 2 m/s/(0. 06 m·3, 14) n = 10, 6 1/s 4. m = 150 kg F = (m·Δv)/Δt Δv = 36 km/h= 10 m/s Δt = (m·Δv)/F F = 300 N Δt = (150 kg · 10 m/s)/300 N Δt = ? Δt = 5 s

Számításos fizika feladatok 5. A kétkarú emelő egyik oldalán a forgástengelytől 60 cm-re 6 kg, 35 cm-re 8 kg tömegű test van felfüggesztve. A másik oldalon a forgástengelytől 40 cm-re 2 kg tömegű test függ. Ezen az oldalon mekkora erővel lehet az emelőt egyensúlyban tartani a forgástengelytől 70 cm távolságban? (80 N)

Számításos fizika feladatok-megoldása n 5. k 1 = 60 cm F 1 = 60 N k 2 = 35 cm F 2 = 80 N k 3 = 40 cm F 3 = 20 N k 4 = 70 cm F 4 = ? F F 1 F 3 F 2 M 1 + M 2 = M 3 + M 4 F 1·k 1 + F 2·k 2 = F 3·k 3 + F 4·k 4 F 4 = (F 1·k 1 + F 2·k 2 - F 3·k 3)/k 4 F 4 = 80 N 4

Számításos fizika feladatok 6. Egy 50 m mély sóbányából 1, 1 g/cm 3 sűrűségű sóoldatot kell a felszínre emelni úgy, hogy percenként 360 liter oldat távozzon. Mekkora teljesítménnyel kell a szivattyút üzemeltetni? (3, 3 k. Watt) 7. Egy bronzszobor tömege 20 kg. Számítsuk ki, mennyi a bronz sűrűsége, ha az 84 % rezet, 10 % cinket és 6 % ónt tartalmaz! (8695, 65 kg/m 3 )

Számításos fizika feladatokmegoldása n 6. s = 50 m ρ = 1, 1 g/cm 3 = 1100 kg/m 3 t = 60 s V = 360 l = 360 dm 3 = 0, 36 m 3 P=? P = W/t = F·s/t = m·g·s/t P = ρ·V·g·s/t P = 1100 kg/m 3 ·0, 36 m 3 ·10 m/s 2 ·50 m/60 s P = 3300 Watt = 3, 3 k. Watt

Számításos fizika feladatokmegoldása n 7. m = 20 kg mr = 20 kg ·0, 84 = 16, 8 kg ρr = 8960 kg/m 3 V r = mr / ρ r Vr = 16, 8 kg/8960 kg/m 3 mc = 20 kg ·0, 1 = 2 kg Vr = 1, 87·10 -3 m 3 ρc = 7136 kg/m 3 V c = mc / ρ c mó = 20 kg · 0, 06 = 1, 2 kg Vc = 2 kg/7136 kg/m 3 ρó = 7300 kg/m 3 Vc = 2, 8 ·10 -4 m 3 ρötv. = ? V ó = mó / ρ ó Vó = 1, 2 kg/7300 kg/m 3 Vó = 1, 64 ·10 -4 m 3 Vö = 2, 3 ·10 -3 m 3 ρötv. = mö /Vö = 20 kg/ 2, 3 ·10 -3 m 3 ρötv = 8695, 65 kg/m 3

Számításos fizika feladatok 8. 40 kg-os gyerek korcsolyán állva 2*105 Pa nyomást gyakorol a jégre. Mekkora felületű egy-egy korcsolya éle? (1000 mm 2) 9. Mekkora erővel tarthatjuk a vízben a 10 dm 3 térfogatú, 2, 6 g/cm 3 sűrűségű követ? (160 N)

Számításos fizika feladatok-megoldása n 8. m = 40 kg F = G = 400 N p = 2·105 Pa A=? p = F/A A = F/p A = 400 N/2·105 Pa A = 2 ·10 -3 m 2 A = 2000 mm 2 A 1 = 1000 mm 2

Számításos fizika feladatok-megoldása n 9. V = 10 dm 3 = 0, 01 m 3 ρt = 2, 6 g/cm 3 = 2600 kg/m 3 Ft = ? Ft = G – F f G = m · g = ρ t· V · g G = 2600 kg/m 3 ·0, 01 m 3 ·10 m/s 2 G = 260 N Ff = ρvíz · Vbem. rész ·g Ff = 1000 kg/m 3 ·0, 01 m 3 ·10 m/s 2 Ff = 100 N Ft = G – F f Ft = 260 N – 100 N = 160 N

Számításos fizika feladatok 10. Egy test tömege 337, 5 kg. Vízbe merítve 2125 N erővel lehet megtartani. Mekkora a test térfogata és milyen anyagból készülhetett? (0, 125 m 3; alumínium) 11. Egy 0, 5 g/cm 3 sűrűségű fából készült téglatest élei 24 cm, 12 cm és 6 cm hosszúak. Milyen mélyre süllyed a vízben, ha a legnagyobb lapján úszik? (3 cm)

Számításos fizika feladatokmegoldása n ρt ρt 10. m = 337, 5 kg Ft = G - F f G = 3375 N Ff = G - F t Ft = 2125 N Ff = 3375 N – 2125 N ρvíz = 1000 kg/m 3 Ff = 1250 N Vbem. rész = ? Ff = ρvíz · g · Vbem. rész ρt = ? Vb. r. = Ff / ρvíz · g Vb. r. = 1250 N/(1000 kg/m 3 · 10 m/s 2 ) Vb. r = 0, 125 m 3 = m/ Vb. r = 337, 5 kg/ 0, 125 m 3 = 2700 kg/m 3

Számításos fizika feladatok-megoldása n 11. ρfa = 0, 5 g/cm 3 = 500 kg/m 3 c = 6 cm ρvíz = 1 g/cm 3 = 1000 kg/m 3 x=?

Számításos fizika feladatok 12. A hidrogénnel töltött léggömb térfogata 1500 m 3. A gondola súlya 2500 N. Fel tud-e emelni ez a léggömb 5 utast, ha azok átlag 65 kg tömegűek? Számítással igazolja állítását! (igen) 13. Egy tengeralattjáró mentőajtaja 0, 6 m 2 területű. Mekkora az ajtókra ható nyomóerő, ha az ajtó 5 m mélyen van a tengervízben? A tengervíz sűrűsége 1030 kg/m 3. (30, 9 k. N)

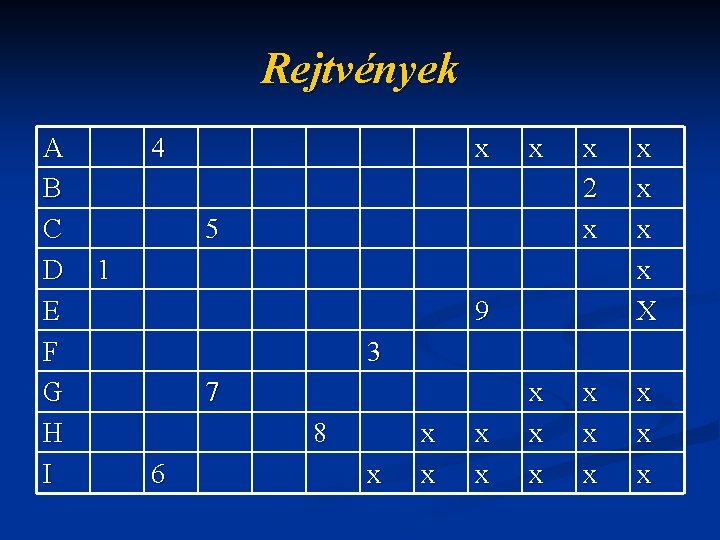
Rejtvények A B C D E F G H I 4 x x x 2 x x x X x x x x x 5 1 9 3 7 8 6 x x x

Rejtvények n n n n n A. A folyadékok hőtágulásán alapuló eszköz. B. Kis belső átmérőjű cső. C. A levegő súlyából származó nyomás. D. Az erőhatás irányába eső és támadásponton átmenő egyenes. E. Az egyenes vonalú, egyenletesen változó mozgás egy fajtája. F. A Föld sajátos környezete (………. . mező). G. Az erő ikertestvére. H. A nyomóerő és a nyomott felület hányadosaként számolhatjuk. I. A munkavégzés során bekövetkező energiaváltozás.

Rejtvények A. B. C. D. E. F. G. H. I. L H L 1 H S G E N M Á4 A É A Z R L Y U 6 Z J G 5 T A A L 7 O N M S N Á B V E M K É Z Y S A I N Á8 A R Á O V D T 3 E S X Ő L M O E Á R X X X C Á N S 9 C Ő X X X S S A É I X X Ő 2 X L S Ó X X X X S X X X

Rejtvények 1. Newton ezzel is foglalkozott. n 2. A béta-sugárzás ……-ból áll. n 3. A fénynek ilyen tulajdonsága is van. n 4. A hőmérséklet mértékegysége n 5. Kepler is foglalkozott vele. n 6. A részecskék között ható erő. n 7. Szétszórtan veri vissza a fénysugarakat n

Rejtvények 1. 2 2. 3. 1 8 7 10 4 5. 9 7. 3 6 5 14 4. 6. 13 x x 11 x x - 12 x x x x x

Rejtvények C S I L L E K 8 T R 1 R É 6 A T X X O 13 S Z Á N 5 O K X X C S 7 K E X X X N X X X X T Á C I Ó S X X X 11 I Z O R Ó S X X X Ú - 12 Ü K Ö R X K E G R 14 Z E S L 10 4 I V A V 9 I K O H 3 D O É M B 2 A G

Rejtvények Keressen a betűhalmazban függőlegesen, vízszintesen, vagy átlósan olyan fizikai kifejezéseket, amelyek a hőerőgépekkel kapcsolatosak! (6 vízszintes, 7 függőleges, 2 átlós kifejezés van elrejtve a rejtvényben. )

Rejtvények n n n n TMUNKAÜTEMOR UGG Á ZTURBI NA R SŐ P S ZELEPAK B I Z Y C W AK N H S É I J G Í B P C OZ K L T NÖ É S V N M T I D K A ALPOCÁ S H NUIM LÁBT OR SZ MGPO AWATTŰRH OAUT PUKORNXE TTF O ÁKDÍZELM OTO R T O T E M N Y OR Y G ASÉ Z S L E X B L Ú Á VS U G Á R H A J T Á SY

Rejtvények n Vízszintes: munkaütem, gázturbina, szelep, Watt, dízelmotor, sugárhajtás n Függőleges: turbinalapát, gőzgép, benzinmotor, rakétamotor, Ottó, dugattyú n Átló: szívás, sűrítés

Rejtvények

Rejtvények

Rejtvények