Statistische Grundlagen Mae fr die zentrale Tendenz Mittelwerte

Statistische Grundlagen - Maße für die zentrale Tendenz (Mittelwerte) - Streuungsmaße - Zusammenhangsmaße

Beschreibende (deskriptive) Statistik Arbeitsablauf der statistischen Bearbeitung von Testergebnissen 1. Ordnung und Darstellung verhältnisskalierter Daten • Tabellarische Ordnung 1. Urliste 2. Primäre Tafel 3. Häufigkeitstabelle (evtl. mit Klassenbildung) • Graphische Darstellung 1. Histogramm oder Polygonzug 2. Berechnung des 1. Modus 2. Median 3. arithmetischen Mittels x

Skalenniveaus • Verhältnisskala • absoluter Nullpunkt • Rangordnung • gleiche Abstände • Beispiele: m, kg, s, Temperaturskala in °K • Intervallskala • Rangordnung • gleiche Abstände • Beispiel: Temperaturskala in °C • Ordinalskala • Rangordnung • Beispiele: Plazierungen, trifft zu - trifft weniger zu - trifft nicht zu • Nominalskala • keine Voraussetzungen • Beispiel: Ja/Nein

Median (Zentralwert) - Wert, bei dem 50% der Messwerte erreicht (kummuliert) sind. - Ermittlung aus einer geordneten Reihe von Messwerten. i 100 m-Zeit [s] 1 5 12, 9 13, 0 13, 3 14, 0 14, 5 6 14, 9 2 3 4 Median bei 5 Messwerten: 13, 3 s Median bei 6 Messwerten: 13, 65 s (13, 3 + 14, 0): 2 Voraussetzung: mindestens Ordinalskala!

Modus (Gipfelwert) - Wert, der am häufigsten vorkommt. i Hochsprunghöhe [m] Anzahl n 1 1, 35 3 2 1, 40 4 3 1, 45 8 4 1, 50 6 5 1, 55 6 1, 60 3 2 7 1, 65 1 Modus bei 1, 45 m Voraussetzung: Nominalskala

Mittelwert (x) i Kugel (x. K) Speer (x. S) 1 16, 00 45, 68 2 15, 66 55, 24 3 16, 30 46, 62 4 13, 77 35, 82 5 13, 11 41, 84 6 13, 39 38, 64 7 13, 11 35, 42 8 15, 12 43, 40 9 12, 63 35, 64 10 13, 21 38, 24 S 142, 30 416, 54 x 14, 23 41, 65 Voraussetzung: mindestens Intervallskala!

Beschreibende (deskriptive) Statistik Arbeitsablauf der statistischen Bearbeitung von Testergebnissen 1. Ordnung und Darstellung verhältnisskalierter Daten • Tabellarische Ordnung 1. Urliste 2. Primäre Tafel 3. Häufigkeitstabelle (evtl. mit Klassenbildung) • Graphische Darstellung 1. Histogramm oder Polygonzug 2. Berechnung des Maße für die zentrale Tendenz 1. Modus 2. Median 3. arithmetisches Mittels x • Berechnung der Streuungsmaße 1. Variationsbreite (Range), R = xmax - xmin 2. Standardabweichung s 3. Variabiltätskoeffizient v

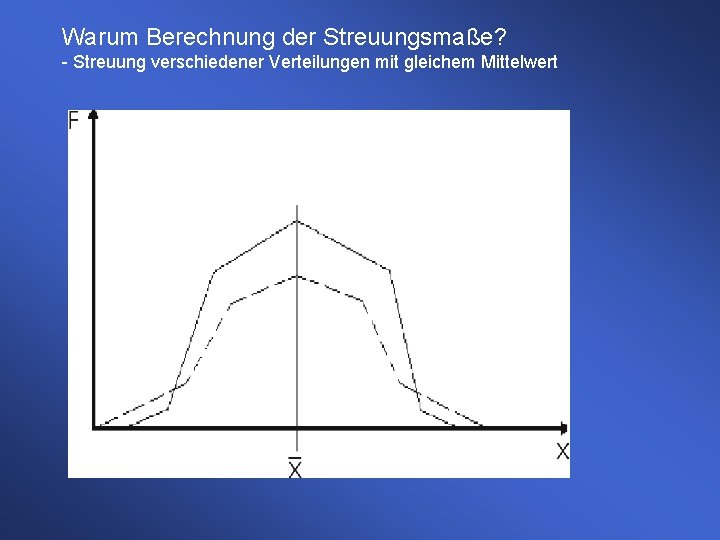
Warum Berechnung der Streuungsmaße? - Streuung verschiedener Verteilungen mit gleichem Mittelwert

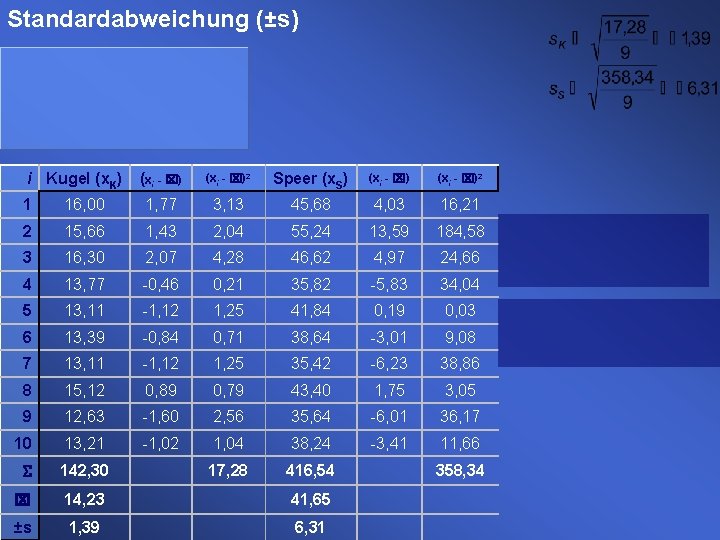
Standardabweichung (±s) i Kugel (x. K) (xi - x)2 Speer (x. S) (xi - x)2 1 16, 00 1, 77 3, 13 45, 68 4, 03 16, 21 2 15, 66 1, 43 2, 04 55, 24 13, 59 184, 58 3 16, 30 2, 07 4, 28 46, 62 4, 97 24, 66 4 13, 77 -0, 46 0, 21 35, 82 -5, 83 34, 04 5 13, 11 -1, 12 1, 25 41, 84 0, 19 0, 03 6 13, 39 -0, 84 0, 71 38, 64 -3, 01 9, 08 7 13, 11 -1, 12 1, 25 35, 42 -6, 23 38, 86 8 15, 12 0, 89 0, 79 43, 40 1, 75 3, 05 9 12, 63 -1, 60 2, 56 35, 64 -6, 01 36, 17 10 13, 21 -1, 02 1, 04 38, 24 -3, 41 11, 66 S 142, 30 17, 28 416, 54 x 14, 23 41, 65 ±s 1, 39 6, 31 358, 34

Standardabweichung (±s) Variabilitätskoeffizient (v) Z-Transformation XK 5=13, 11 XS 5=41, 84

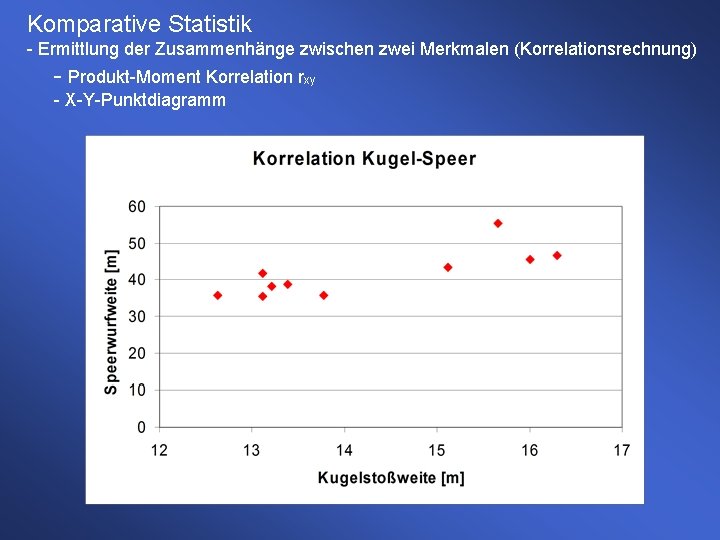
Komparative Statistik - Ermittlung der Zusammenhänge zwischen zwei Merkmalen (Korrelationsrechnung) - Produkt-Moment Korrelation rxy - X-Y-Punktdiagramm

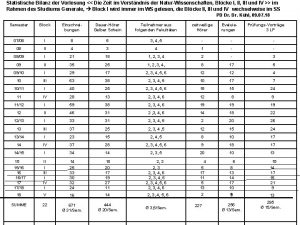
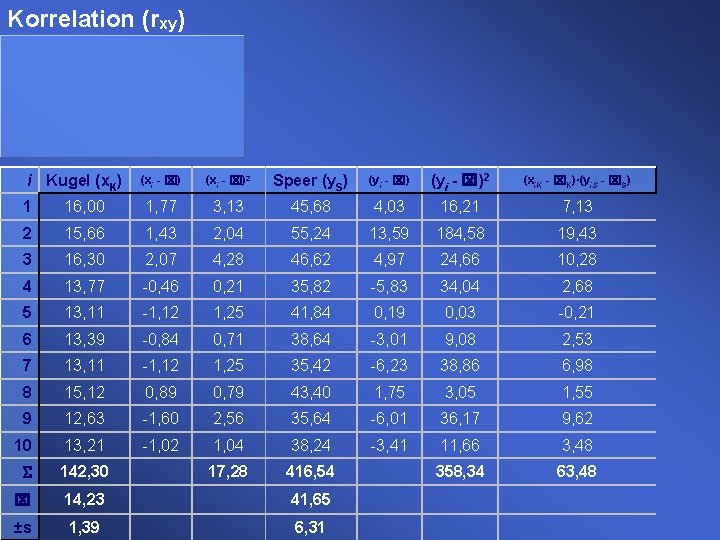
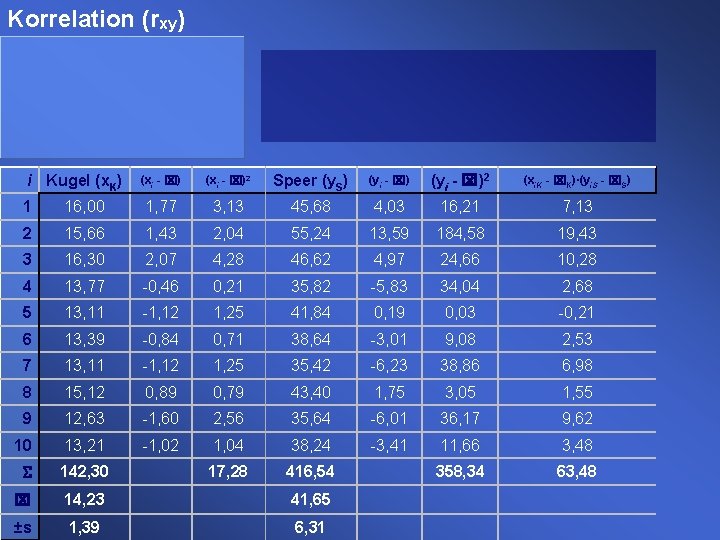
Korrelation (rxy) i Kugel (x. K) (xi - x)2 Speer (y. S) (yi - x)2 (xi. K - x. K)·(yi. S - x. S) 1 16, 00 1, 77 3, 13 45, 68 4, 03 16, 21 7, 13 2 15, 66 1, 43 2, 04 55, 24 13, 59 184, 58 19, 43 3 16, 30 2, 07 4, 28 46, 62 4, 97 24, 66 10, 28 4 13, 77 -0, 46 0, 21 35, 82 -5, 83 34, 04 2, 68 5 13, 11 -1, 12 1, 25 41, 84 0, 19 0, 03 -0, 21 6 13, 39 -0, 84 0, 71 38, 64 -3, 01 9, 08 2, 53 7 13, 11 -1, 12 1, 25 35, 42 -6, 23 38, 86 6, 98 8 15, 12 0, 89 0, 79 43, 40 1, 75 3, 05 1, 55 9 12, 63 -1, 60 2, 56 35, 64 -6, 01 36, 17 9, 62 10 13, 21 -1, 02 1, 04 38, 24 -3, 41 11, 66 3, 48 S 142, 30 17, 28 416, 54 358, 34 63, 48 x 14, 23 41, 65 ±s 1, 39 6, 31

Korrelation (rxy) i Kugel (x. K) (xi - x)2 Speer (y. S) (yi - x)2 (xi. K - x. K)·(yi. S - x. S) 1 16, 00 1, 77 3, 13 45, 68 4, 03 16, 21 7, 13 2 15, 66 1, 43 2, 04 55, 24 13, 59 184, 58 19, 43 3 16, 30 2, 07 4, 28 46, 62 4, 97 24, 66 10, 28 4 13, 77 -0, 46 0, 21 35, 82 -5, 83 34, 04 2, 68 5 13, 11 -1, 12 1, 25 41, 84 0, 19 0, 03 -0, 21 6 13, 39 -0, 84 0, 71 38, 64 -3, 01 9, 08 2, 53 7 13, 11 -1, 12 1, 25 35, 42 -6, 23 38, 86 6, 98 8 15, 12 0, 89 0, 79 43, 40 1, 75 3, 05 1, 55 9 12, 63 -1, 60 2, 56 35, 64 -6, 01 36, 17 9, 62 10 13, 21 -1, 02 1, 04 38, 24 -3, 41 11, 66 3, 48 S 142, 30 17, 28 416, 54 358, 34 63, 48 x 14, 23 41, 65 ±s 1, 39 6, 31

Interpretation des Korrelationskoeffizienten • Korrelationskoeffizienten bewegen sich im Bereich von -1 bis +1. • Positive Korrelationen ergeben sich bei Zusammenhängen der Art „je größer die eine Variable, desto größer die andere Variable“ • Negative Korrelationen ergeben sich bei Zusammenhängen der Art „je größer die eine Variable, desto kleiner die andere Variable“ • Werte zwischen 0, 7 und 1, 0 werden als hohe, Werte zwischen 0, 3 und 0, 7 als mittlere und Werte zwischen 0 und 0, 3 als niedrige Korrelationen bezeichnet. Ein Wert von -1 oder +1 beschreibt einen vollständigen Zusammenhang. • Die Korrelationsberechnung kann z. B. zur Identifikation von wichtigen biomechanischen Parametern (Kennwerten) und zur Abgrenzung von eher unwichtigen dienen.

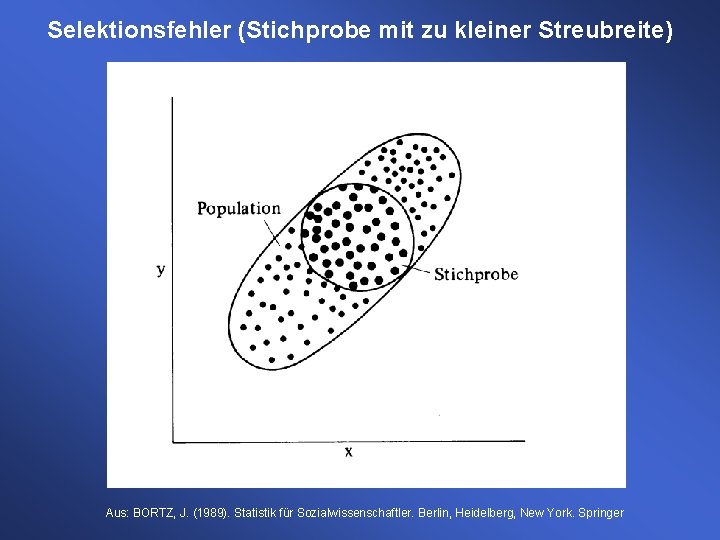
Einschränkungen zum Korrelationskoeffizienten • Nur sinnvoll anwendbar bei linearen Zusammenhängen! Für nichtlineare Zusammenhänge existieren andere Verfahren • Ein hoher Korrelationskoeffizient sagt noch nichts über einen tatsächlich inhaltlich vorhandenen Zusammenhang aus (Scheinkorrelationen)! • Durch die falsche Auswahl von Populationen (Selektionsfehler) können Verzerrungen entstehen.

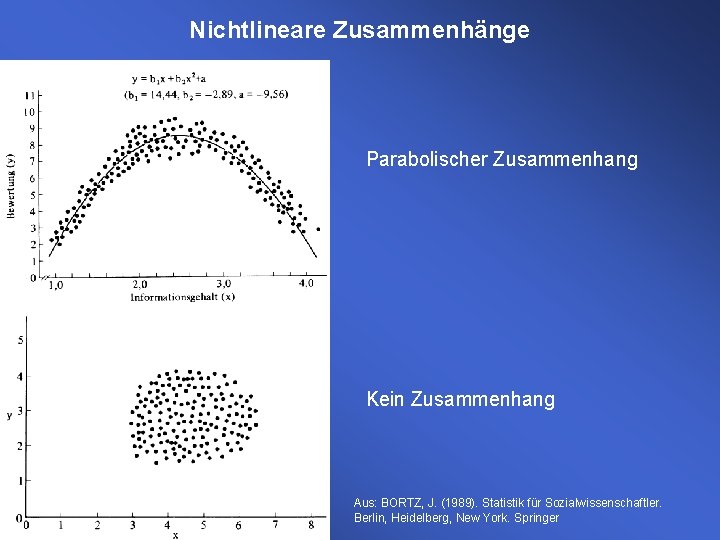
Nichtlineare Zusammenhänge Parabolischer Zusammenhang Kein Zusammenhang Aus: BORTZ, J. (1989). Statistik für Sozialwissenschaftler. Berlin, Heidelberg, New York. Springer

Scheinkorrelation

Scheinkorrelation? Sind gute Golfspieler gegenüber schlechteren die besseren oder die schlechteren Unternehmensführer? Wer erreicht die besseren Renditen? Was meinen Sie? Argumente? Begründungen? Was braucht man zum Golferfolg? Disziplin? Konzentration? Scheinbar korreliert ein kleines Handicap im Golf mit hohen Renditen durch den Vorstandsvorsitzenden (negative Korrelation)! Ob dies allerdings inhaltlich begründbar ist, bleibt fraglich. Wäre Tiger Woods also der ideale Unternehmensführer?

Selektionsfehler (Stichprobe mit zu kleiner Streubreite) Aus: BORTZ, J. (1989). Statistik für Sozialwissenschaftler. Berlin, Heidelberg, New York. Springer

Selektionsfehler (Stichprobe mit zu kleiner Streubreite) Aus: BORTZ, J. (1989). Statistik für Sozialwissenschaftler. Berlin, Heidelberg, New York. Springer

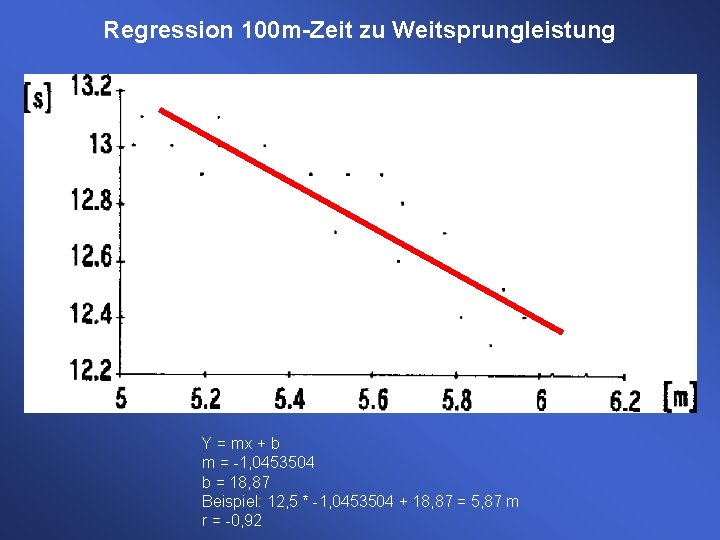
Regression 100 m-Zeit zu Weitsprungleistung Y = mx + b m = -1, 0453504 b = 18, 87 Beispiel: 12, 5 * -1, 0453504 + 18, 87 = 5, 87 m r = -0, 92

Testverfahren für Gruppenvergleiche (Mittelwertsvergleiche) Aus: WILLIMCZIK, K. (1997): Statistik im Sport. Hamburg: Czwalina

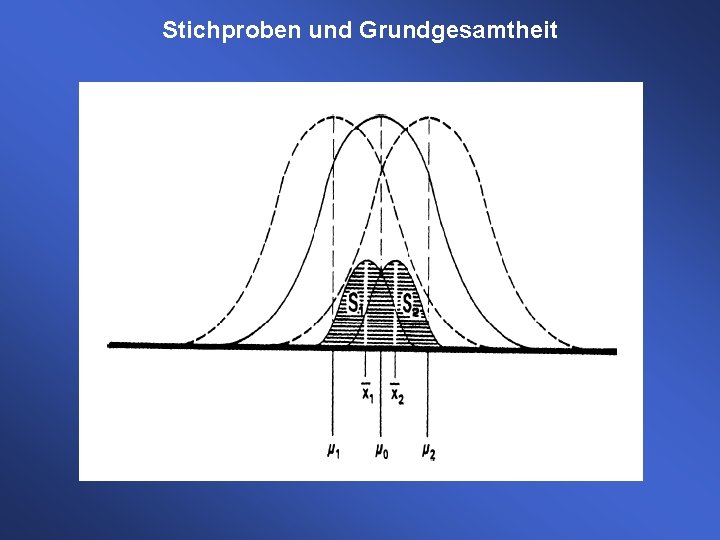
Stichproben und Grundgesamtheit

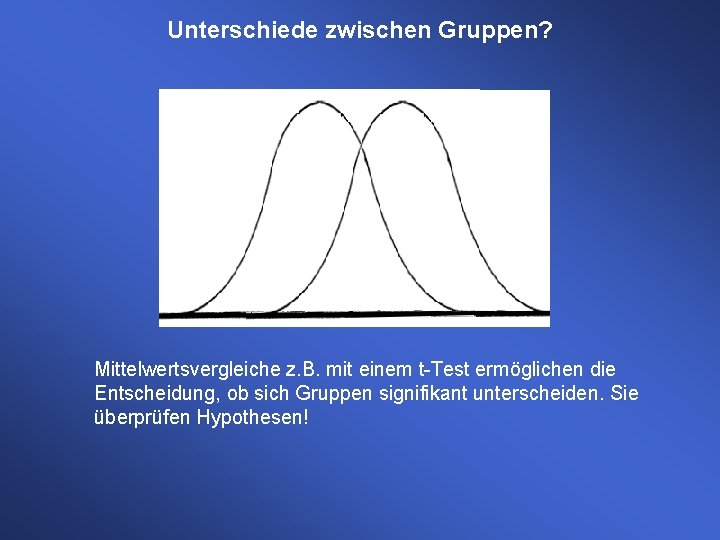
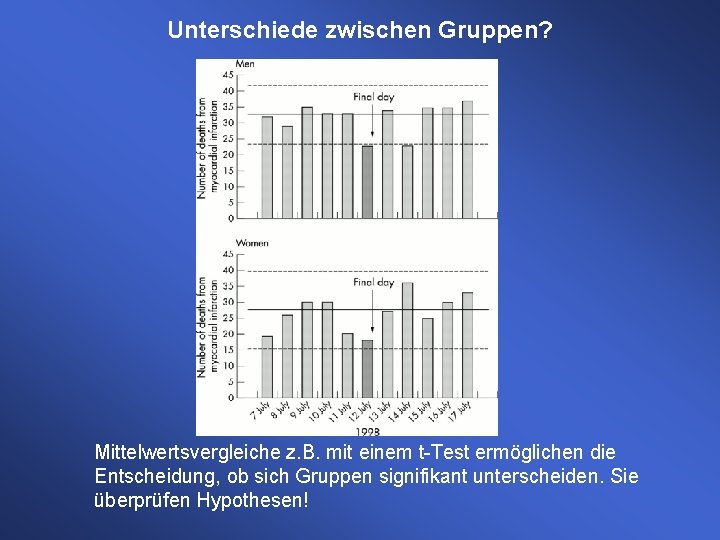
Unterschiede zwischen Gruppen? Mittelwertsvergleiche z. B. mit einem t-Test ermöglichen die Entscheidung, ob sich Gruppen signifikant unterscheiden. Sie überprüfen Hypothesen!

Unterschiede zwischen Gruppen? Mittelwertsvergleiche z. B. mit einem t-Test ermöglichen die Entscheidung, ob sich Gruppen signifikant unterscheiden. Sie überprüfen Hypothesen!