Mae der zentralen Tendenz Modalwert Modus hufigster Wert

Maße der zentralen Tendenz • Modalwert / Modus • häufigster Wert • bei klassifizierten Werten: die Klassenmitte der am stärksten besetzten Klasse • Notation: X Mo • ab Nominalskala • Modus ist nicht die Häufigkeit, sondern die Variablenausprägung • bimodale Verteilungen: 2 häufige Werte

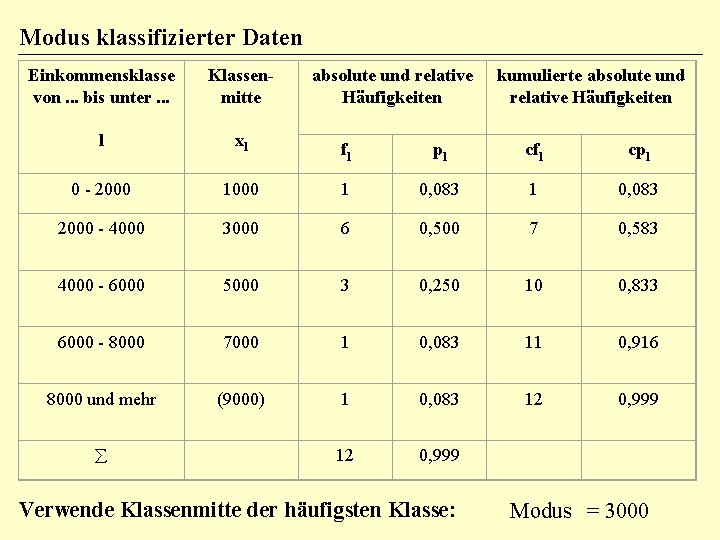
Modus klassifizierter Daten Einkommensklasse von. . . bis unter. . . Klassenmitte l xl 0 - 2000 absolute und relative Häufigkeiten kumulierte absolute und relative Häufigkeiten fl pl cfl cpl 1000 1 0, 083 2000 - 4000 3000 6 0, 500 7 0, 583 4000 - 6000 5000 3 0, 250 10 0, 833 6000 - 8000 7000 1 0, 083 11 0, 916 8000 und mehr (9000) 1 0, 083 12 0, 999 å Verwende Klassenmitte der häufigsten Klasse: Modus = 3000

Median ~ Notation: X (X Tilde) teilt Werte in 2 gleich große Hälften ab Ordinalskala bei ungeradem N: Wert der mittleren Person bei geradem N: Mittelwert der beiden mittleren Personen (dies nur bei Intervallskala) bei mehrfach auftretenden Werten: 3 6 7 8 8 8 9 9 10 12 Uminterpretieren des Medians (mindestens die Hälfte der Personen liegt unter/über 8) oder lineare Interpolation (Median=8. 17 siehe Benninghaus)

Median der 12 Einkommensangaben (1) Als Beispiel dienen die Einkommensangaben aus Diekmann (1995). Die Merkmalswerte müssen in sortierter Form vorliegen (primäre Liste). Der Median entspricht bei ungerader Anzahl von Fällen dem Merkmalswert, der in der sortierten (primären) Liste aller Merkmalswerte auf dem r-ten Rangplatz steht (mit r=(n+1)/2). Dieser Wert teilt die Liste aller Merkmalswerte exakt in zwei Hälften. Bei gerader Anzahl von Fällen gibt es keinen Wert, der die Liste exakt in zwei Hälften unterteilt. Man verwendet alternativ den Durchschnitt aus dem r-ten und (r+1)-ten Wert, wobei r jetzt n/2 entspricht. Der Datensatz von Diekmann enthält zwölf gültige Einkommensangaben, so dass wir in diesem Beispiel von einer geraden Anzahl von Fällen ausgehen müssen.

Median der 12 Einkommensangaben (2) Rang Ein-kommen (i) x(i) 1 1600 2 2300 3 2300 4 2400 5 2900 6 3200 7 3500 8 4500 9 4600 10 5200 11 6500 12 12000 Der Median liegt zwischen dem 6. und 7. Wert. Vereinbart ist der Durchschnitt beider Werte: Median = (3200+3500)/2 = 3350.

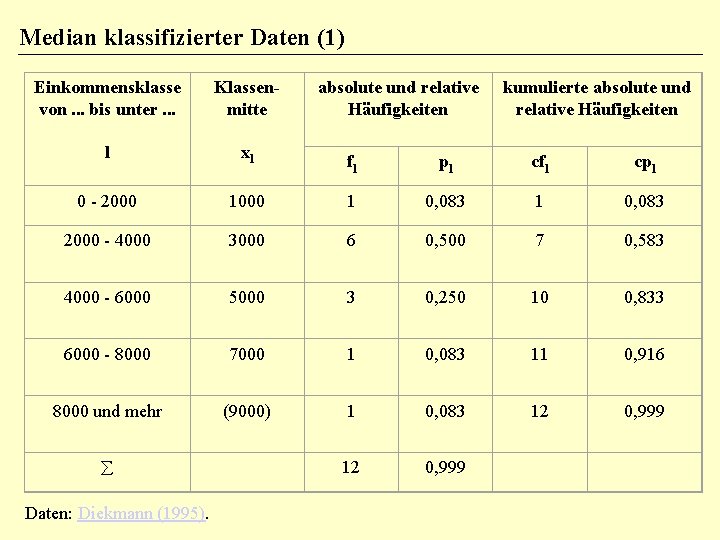
Median klassifizierter Daten (1) Einkommensklasse von. . . bis unter. . . Klassenmitte l xl 0 - 2000 absolute und relative Häufigkeiten kumulierte absolute und relative Häufigkeiten fl pl cfl cpl 1000 1 0, 083 2000 - 4000 3000 6 0, 500 7 0, 583 4000 - 6000 5000 3 0, 250 10 0, 833 6000 - 8000 7000 1 0, 083 11 0, 916 8000 und mehr (9000) 1 0, 083 12 0, 999 å Daten: Diekmann (1995).

Median klassifizierter Daten (2) Verwende lineare Interpolation im Medianintervall 2000 -4000 = Medianintervall 2000 = cmu (exakte untere Grenze des Medianintervalls) 12 = n (Stichprobenumfang) 1 = cfu (kumulierte Häufigkeit unterhalb des Medianintervalls) 6 = fm (Häufigkeit im Medianintervall) 2000 = cmo - cmu (Breite des Medianintervalls) Median = cmu + [(n/2 - cfu). (cmo - cmu) / fm] 3666, 67 DM = 2000 + [(12/2 - 1). 2000 / 6]

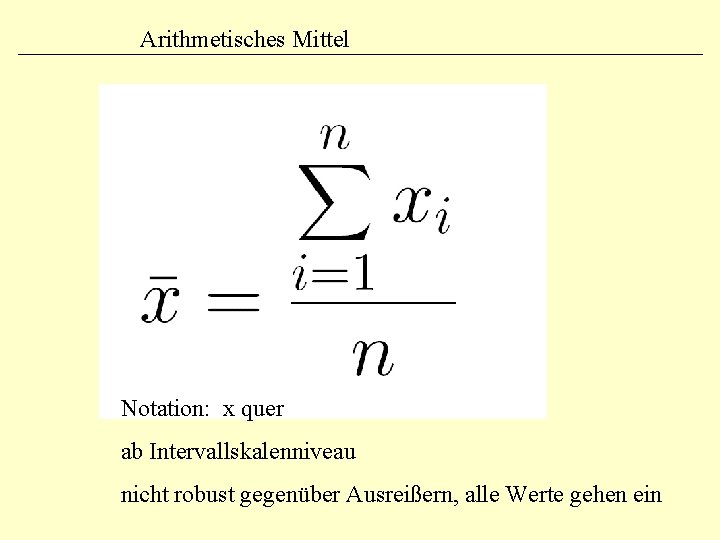
Arithmetisches Mittel Notation: x quer ab Intervallskalenniveau nicht robust gegenüber Ausreißern, alle Werte gehen ein

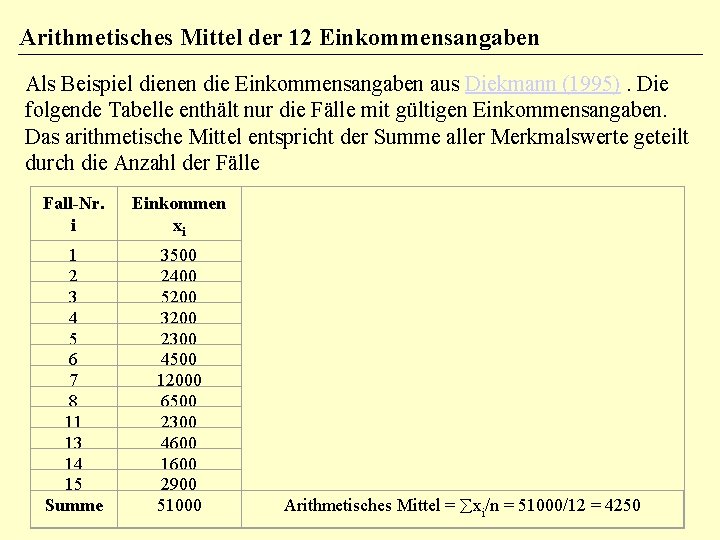
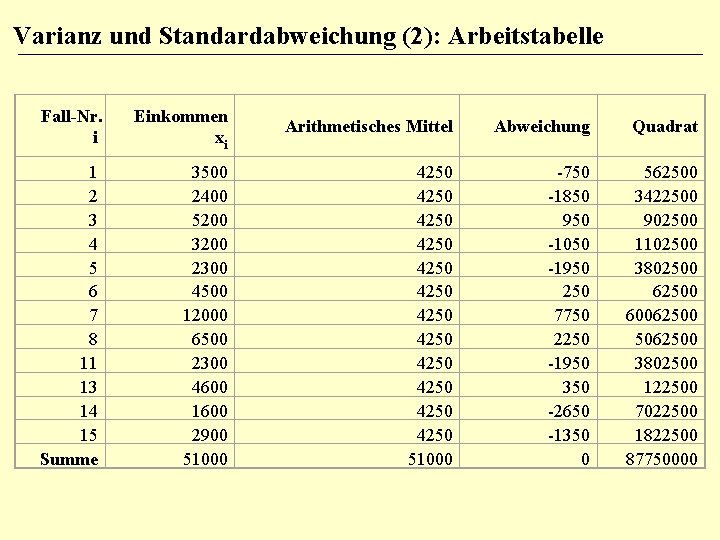
Arithmetisches Mittel der 12 Einkommensangaben Als Beispiel dienen die Einkommensangaben aus Diekmann (1995). Die folgende Tabelle enthält nur die Fälle mit gültigen Einkommensangaben. Das arithmetische Mittel entspricht der Summe aller Merkmalswerte geteilt durch die Anzahl der Fälle Fall-Nr. i Einkommen xi 1 2 3 4 5 6 7 8 11 13 14 15 Summe 3500 2400 5200 3200 2300 4500 12000 6500 2300 4600 1600 2900 51000 Arithmetisches Mittel = åxi/n = 51000/12 = 4250

Arbeitstabelle für MW bei gruppierten Daten xi 1 2 3 fi 5 7 2 fi xi 5 14 6 Summe 14 Summe = 25 MW=25/14

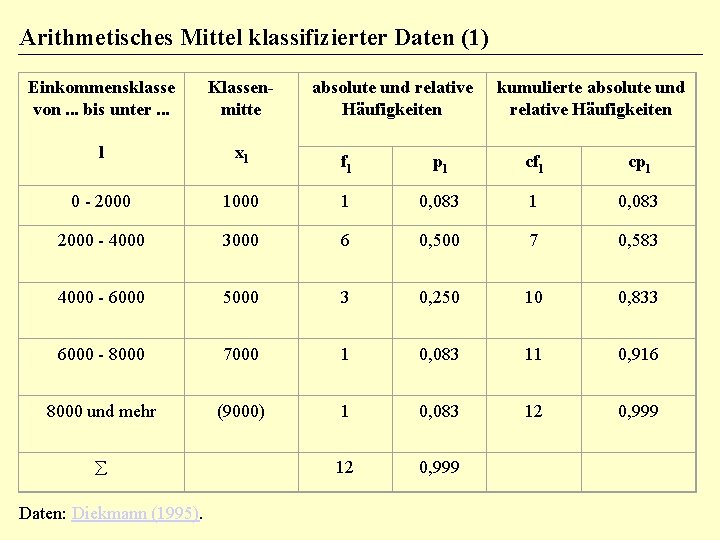
Arithmetisches Mittel klassifizierter Daten (1) Einkommensklasse von. . . bis unter. . . Klassenmitte l xl 0 - 2000 absolute und relative Häufigkeiten kumulierte absolute und relative Häufigkeiten fl pl cfl cpl 1000 1 0, 083 2000 - 4000 3000 6 0, 500 7 0, 583 4000 - 6000 5000 3 0, 250 10 0, 833 6000 - 8000 7000 1 0, 083 11 0, 916 8000 und mehr (9000) 1 0, 083 12 0, 999 å Daten: Diekmann (1995).

Arithmetisches Mittel klassifizierter Daten (2) Verwende Klassenmitten Arithm. Mittel = (1. 1000 + 6. 3000 + 3. 5000 + 1. 7000 + 1. 9000) / 12 = 50000 / 12 = 4166, 67 DM = 0, 083. 1000 + 0, 500. 3000 + 0, 250. 5000 + 0, 083. 7000 + 0, 083. 9000

Spannweite Die Merkmalswerte müssen in sortierter Form vorliegen (primäre Liste). Die Spannweite der Verteilung entspricht der Differenz zwischen dem kleinsten und dem größten Merkmalswert. Dazu ist metrisches Skalenniveau erforderlich (Intervallskala). Bei ordinalen Skalen begnügt man sich mit der Angabe des kleinsten und größten Werts (min, max). Bei klassifizierten Daten: Differenz zwischen der Klassenmitte der obersten Klasse und der untersten Klasse. Der Wert ist sensibel für Ausreißer (erfasst nur ! Ausreißer), daher besser Quartilsabstand (umfasst die mittleren 50%).

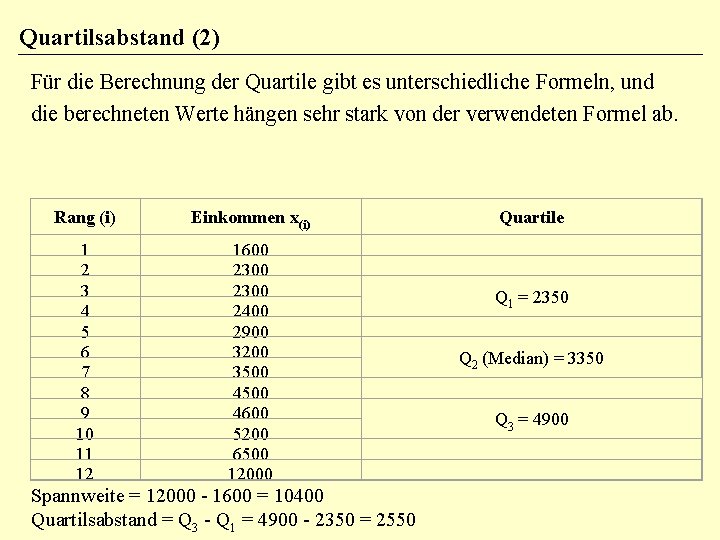
Quartilsabstand (1) Ähnlich wie der Median die unteren 50% der Merkmalswerte von den oberen 50% trennt, lassen sich beliebige Perzentile einer Verteilung berechnen. Am bekanntesten sind das 25%- und 75%-Perzentil, die das untere und das obere Viertel der Verteilung abschneiden. Man bezeichnet sie daher auch als untere und obere Quartile bzw. als erstes und drittes Quartil (der Median ist quasi das zweite Quartil). Notation: QA. Der Quartilsabstand entspricht der Differenz zwischen dem oberen (dritten) und unteren (ersten) Quartil. Er misst, in welchem Bereich sich die mittleren 50% der Merkmalswerte bewegen. Intervallskala erforderlich. Gebräuchlich ist auch der Semiquartilsabstand (die Hälfte des Quartilsabstands) aufgrund der Vergleichsmöglichkeiten mit der Standardabweichung. (Daten: Diekmann, 1995)

Quartilsabstand (2) Für die Berechnung der Quartile gibt es unterschiedliche Formeln, und die berechneten Werte hängen sehr stark von der verwendeten Formel ab. Rang (i) Einkommen x(i) 1 2 3 4 5 6 7 8 9 10 11 12 1600 2300 2400 2900 3200 3500 4600 5200 6500 12000 Spannweite = 12000 - 1600 = 10400 Quartilsabstand = Q 3 - Q 1 = 4900 - 2350 = 2550 Quartile Q 1 = 2350 Q 2 (Median) = 3350 Q 3 = 4900

Varianz quadrierte aufsummierte Abweichungen vom Mittelwert, geteilt durch n bzw. n-1 (unquadrierte Abweichungen würden immer 0 ergeben). Intervallskalenniveau erforderlich

Varianz und Standardabweichung (1) Die Varianz basiert auf der Summe der quadrierten Abweichungen jedes Merkmalswertes vom arithmetischen Mittel: SAQx. Ihre Berechnung hängt davon ab, ob man Daten einer Totalerhebung oder einer Stichprobe betrachtet: • Stichprobe: Varianz = SAQx / (n-1) • Totalerhebung: Varianz = SAQx / n Dabei entspricht n der Anzahl der Untersuchungseinheiten der Stichprobe bzw. der Totalerhebung. Die Standardabweichung ergibt sich aus der Quadratwurzel der Varianz. Vorteil: Die ursprüngliche Maßeinheit bleibt erhalten, z. B. das Alter weicht durchschnittlich 7 Jahre vom Mittelwert ab.

Varianz und Standardabweichung (2): Arbeitstabelle Fall-Nr. i Einkommen xi Arithmetisches Mittel Abweichung Quadrat 1 2 3 4 5 6 7 8 11 13 14 15 Summe 3500 2400 5200 3200 2300 4500 12000 6500 2300 4600 1600 2900 51000 4250 4250 4250 51000 -750 -1850 950 -1050 -1950 250 7750 2250 -1950 350 -2650 -1350 0 562500 3422500 902500 1102500 3802500 60062500 5062500 3802500 122500 7022500 1822500 87750000

Varianz und Standardabweichung (3) Stichprobe (Divisor n-1=11) Varianz = 87750000 / 11 = 7977272, 73 Standardabweichung = Ö Varianz = Ö 7977272, 73 = 2824, 41 Variationskoeffizient = Standardabweichung / arithm. Mittel = 2824, 41 / 4250 = 0, 66 Wenn es sich bei der Befragung von Diekmann nicht um eine Stichprobe, sondern um eine Totalerhebung gehandelt hätte, hätte man wie folgt rechnen müssen. Grundgesamtheit (Divisor n=12) Varianz = 87750000 / 12 = 7312500, 00 Standardabweichung = Ö Varianz = Ö 7312500, 00 = 2589, 04 Variationskoeffizient = Standardabweichung / arithm. Mittel = 2589, 04 / 4250 = 0, 61

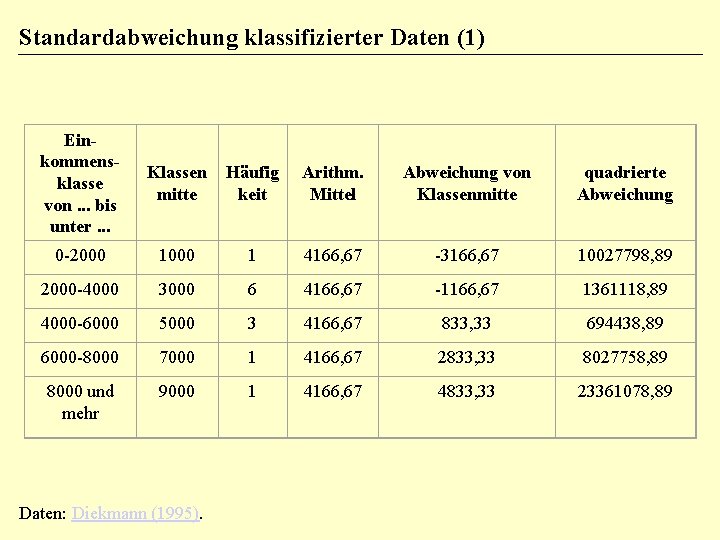
Standardabweichung klassifizierter Daten (1) Einkommensklasse von. . . bis unter. . . Klassen mitte Häufig keit Arithm. Mittel Abweichung von Klassenmitte quadrierte Abweichung 0 -2000 1 4166, 67 -3166, 67 10027798, 89 2000 -4000 3000 6 4166, 67 -1166, 67 1361118, 89 4000 -6000 5000 3 4166, 67 833, 33 694438, 89 6000 -8000 7000 1 4166, 67 2833, 33 8027758, 89 8000 und mehr 9000 1 4166, 67 4833, 33 23361078, 89 Daten: Diekmann (1995).

Standardabweichung klassifizierter Daten (2) Verwende gewichtete Summe der Abweichungsquadrate GSAQx = 1. 10027798, 89 + 6. 1361118, 89 + 3. 694438, 89 + 1. 8027758, 89 + 1. 23361078, 89 = 43472194, 45 Varianz = GSAQx/(n-1) = 43472194, 45 / (12 -1) = 3952017, 68 Standardabweichung = Ö Varianz = Ö 3952017, 68 = 1987, 97

Zusammenfassung der Ergebnisse: Einkommen der Befragten Es wurden 60 männliche Bedienstete der Verwaltung einer westdeutschen Großstadt befragt. Insgesamt 58 Personen machten Angaben über ihr monatliches Nettoeinkommen. Die Einkommen der befragten Personen bewegen sich im Bereich von 1300 DM bis 4300 DM. Sieht man einmal von den extrem niedrigen und den extrem hohen Einkommen ab, dann liegen die mittleren 50% der Einkommen zwischen 1700 DM und 2500 DM. Die Hälfte der befragten Personen verdient weniger als 1950 DM. Im Durchschnitt verdienen die befragten Personen 2118, 79 DM (Standardabweichung 619, 60).

Mittelwerte und Streuungsmaße nach Messniveau (1) Zentrale Tendenz (Mittelwerte) Nominal Ordinal Intervall Verhältnis Modus ja ja Median nein Ja ja ja Arithm. Mittel nein ja ja Geom. Mittel nein ja

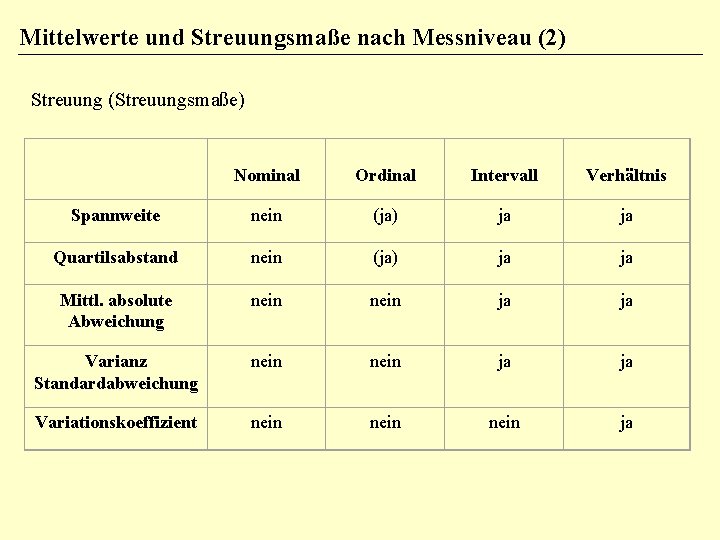
Mittelwerte und Streuungsmaße nach Messniveau (2) Streuung (Streuungsmaße) Nominal Ordinal Intervall Verhältnis Spannweite nein (ja) ja ja Quartilsabstand nein (ja) ja ja Mittl. absolute Abweichung nein ja ja Varianz Standardabweichung nein ja ja Variationskoeffizient nein ja

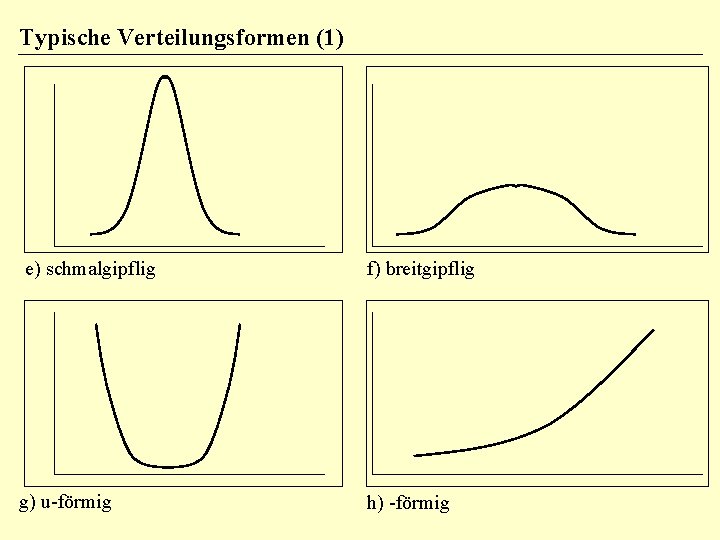
Typische Verteilungsformen (1) e) schmalgipflig f) breitgipflig g) u-förmig h) -förmig

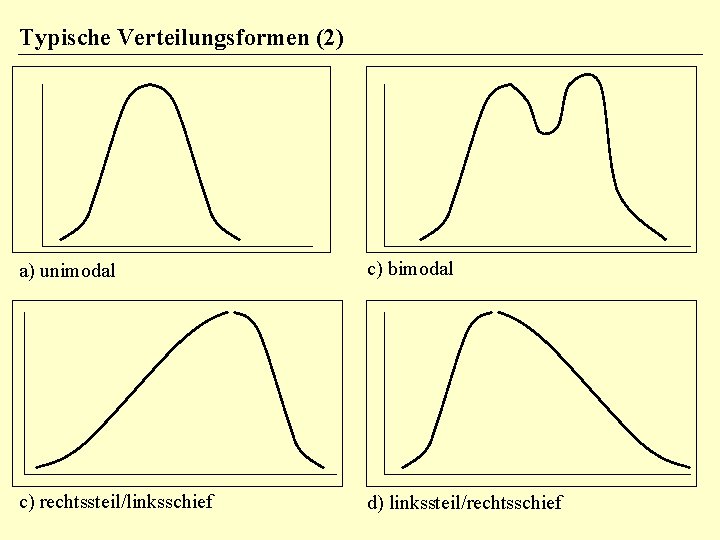
Typische Verteilungsformen (2) a) unimodal c) bimodal c) rechtssteil/linksschief d) linkssteil/rechtsschief

Weitere univariate Statistiken • Schiefe: Maß für die Asymmetrie • Exzess: Maß für die Steilheit

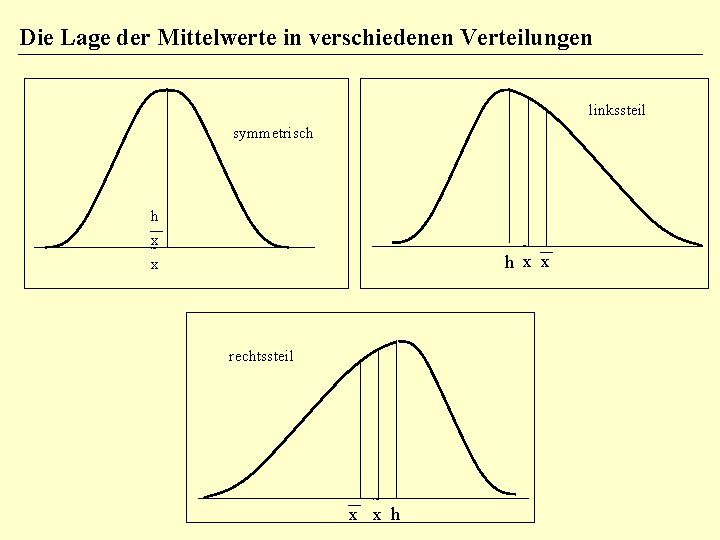
Die Lage der Mittelwerte in verschiedenen Verteilungen linkssteil symmetrisch h x~ x ~ h x x rechtssteil ~ x x h

Vergleich einer Verteilung mit der Standardnormalverteilung • Wenn die relative Stellung einer Person bezogen auf eine Stichprobe in Einheiten der Standardabweichung ermittelt werden soll • oder wenn die Werte zweier Tests einer Person, die mit verschiedenen Maßeinheiten gemessen wurden, verglichen werden sollen, werden die Werte ztransformiert: • zi=xi-xquer / s • symmetrische Verteilungen (Normalverteilungen) werden so in eine Standardnormalverteilung überführt, man kann aus Tabellen ablesen, wie viele Werte unter einem bestimmten Wert liegen.