Statistical Learning Dong Liu Dept EEIS USTC Chapter

Statistical Learning Dong Liu Dept. EEIS, USTC

Chapter 3. Support Vector Machine (SVM) 1. 2. 3. 4. Max-margin linear classification Soft-margin linear classification The kernel trick Efficient algorithm for SVM 2021/12/17 Chap 3. SVM 2

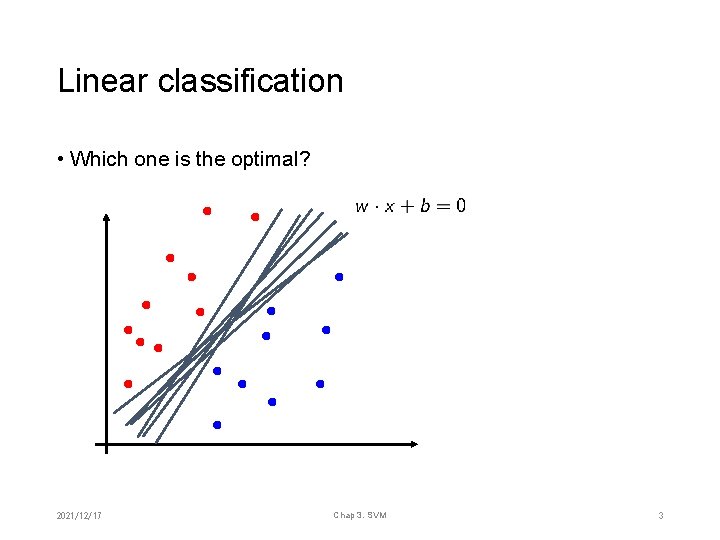
Linear classification • Which one is the optimal? 2021/12/17 Chap 3. SVM 3

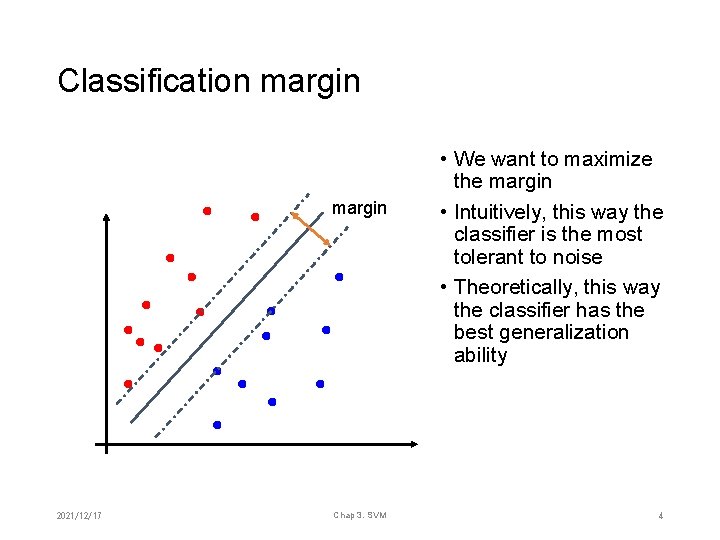
Classification margin 2021/12/17 Chap 3. SVM • We want to maximize the margin • Intuitively, this way the classifier is the most tolerant to noise • Theoretically, this way the classifier has the best generalization ability 4

Geometric margin & Functional margin • For a point , its distance to the decision boundary is • Geometric margin is • Functional margin is • Since we can amplify both and by a scaling factor, without changing the geometric margin, we can set 2021/12/17 Chap 3. SVM 5

Maximize geometric margin 1/2 • The problem is • Equivalent to 2021/12/17 Chap 3. SVM 6

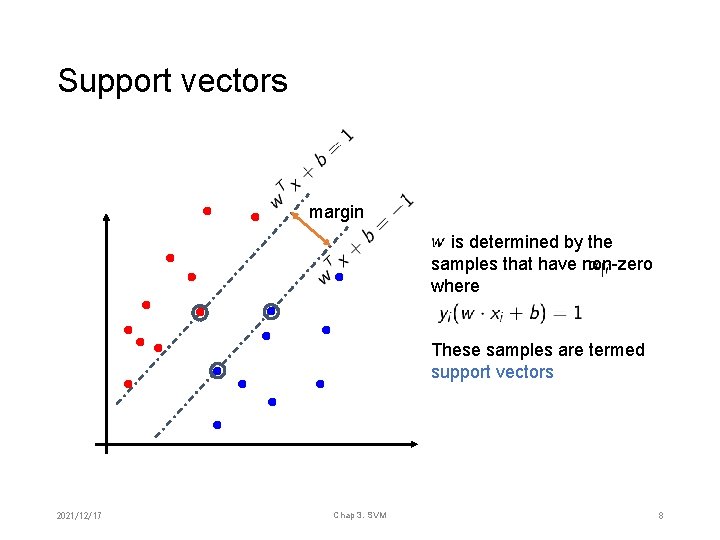
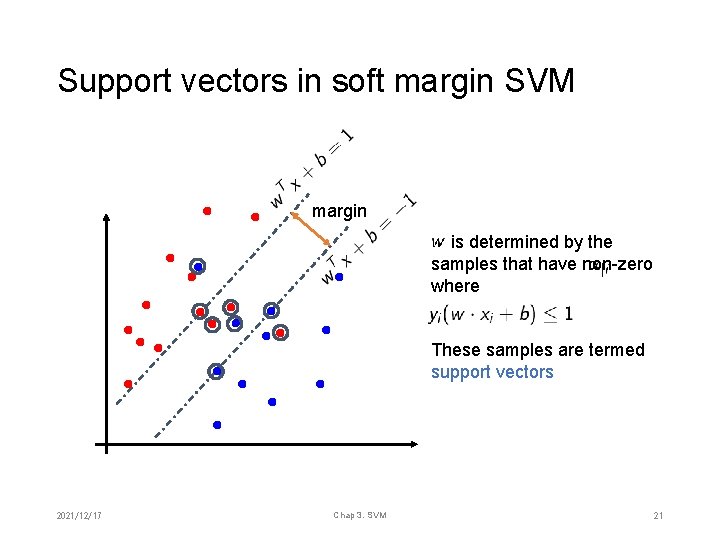
Maximize geometric margin 2/2 • Using the Lagrange multiplier • According to KKT condition is determined by the samples that have non-zero where These samples are termed support vectors 2021/12/17 Chap 3. SVM 7

Support vectors margin is determined by the samples that have non-zero where These samples are termed support vectors 2021/12/17 Chap 3. SVM 8

Lagrange dual of max-margin • Original problem: • Dual problem: • Plus KKT condition: 2021/12/17 Chap 3. SVM 9

Solution of max-margin • Once we have solved the dual problem, we have • Summary: for max-margin classification, we can solve the dual problem to find out support vectors, and then determine the best decision boundary 2021/12/17 Chap 3. SVM 10

Chapter 3. Support Vector Machine (SVM) 1. 2. 3. 4. Max-margin linear classification Soft-margin linear classification The kernel trick Efficient algorithm for SVM 2021/12/17 Chap 3. SVM 11

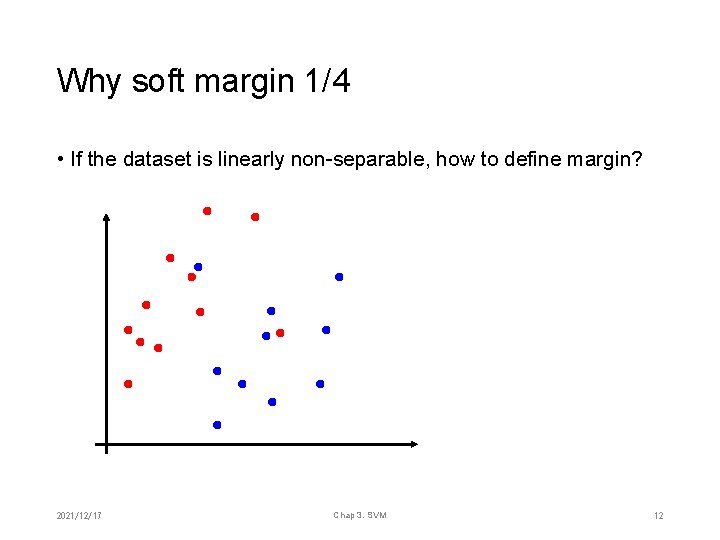
Why soft margin 1/4 • If the dataset is linearly non-separable, how to define margin? 2021/12/17 Chap 3. SVM 12

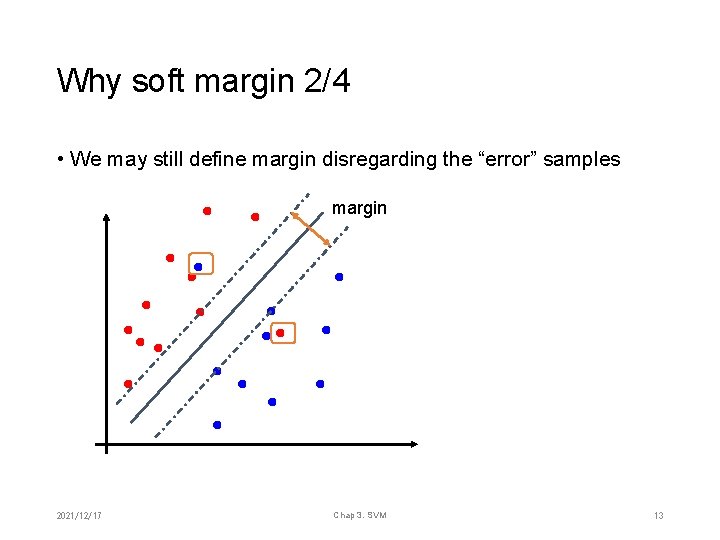
Why soft margin 2/4 • We may still define margin disregarding the “error” samples margin 2021/12/17 Chap 3. SVM 13

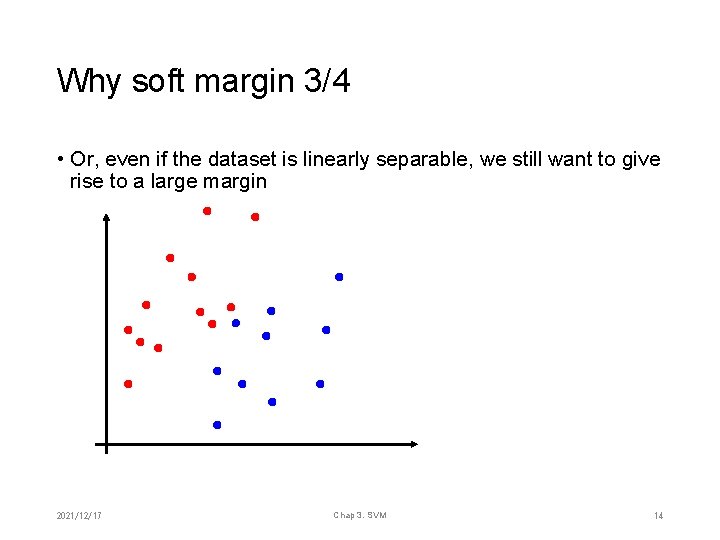
Why soft margin 3/4 • Or, even if the dataset is linearly separable, we still want to give rise to a large margin 2021/12/17 Chap 3. SVM 14

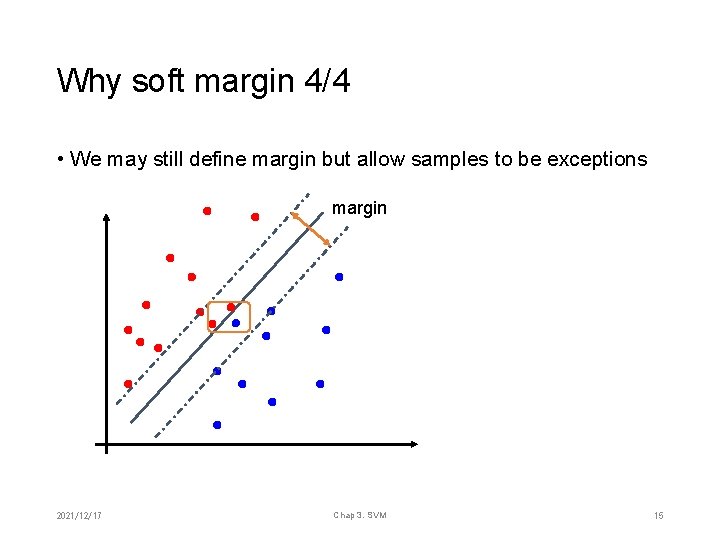
Why soft margin 4/4 • We may still define margin but allow samples to be exceptions margin 2021/12/17 Chap 3. SVM 15

Soft margin formulation 1/3 • We change our objective to where the indicator function is • Compared to the “hard” margin 2021/12/17 Chap 3. SVM 16

Soft margin formulation 2/3 • Using the Lagrange multiplier • Since the indicator function is intractable, we replace it with • So the problem becomes • It can be interpreted as to minimize hinge loss with regularization 2021/12/17 Chap 3. SVM norm 17

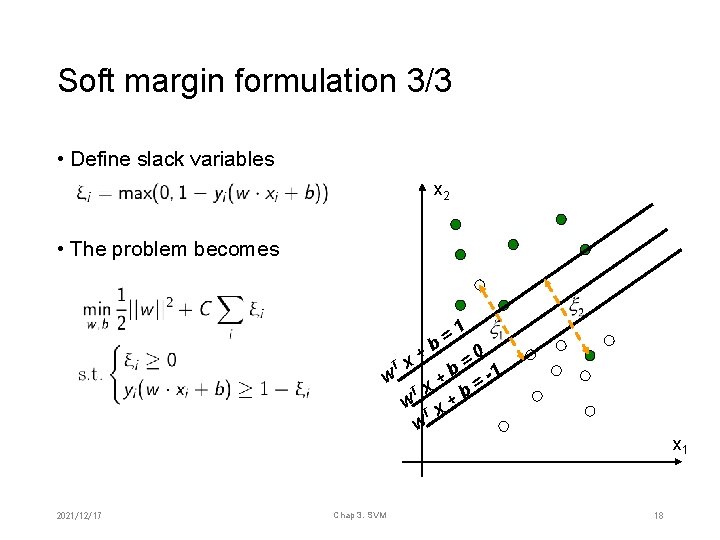
Soft margin formulation 3/3 • Define slack variables x 2 • The problem becomes 1 = b 0 + = T x b -1 w + = T x b w x+ T w 2021/12/17 Chap 3. SVM x 1 18

Soft margin solution 1/2 • Using the Lagrange multiplier • The KKT condition: 2021/12/17 Chap 3. SVM 19

Soft margin solution 2/2 • Thus the Lagrange dual problem is • Samples are categorized into Support vectors 2021/12/17 Chap 3. SVM 20

Support vectors in soft margin SVM margin is determined by the samples that have non-zero where These samples are termed support vectors 2021/12/17 Chap 3. SVM 21

Chapter 3. Support Vector Machine (SVM) 1. 2. 3. 4. Max-margin linear classification Soft-margin linear classification The kernel trick Efficient algorithm for SVM 2021/12/17 Chap 3. SVM 22

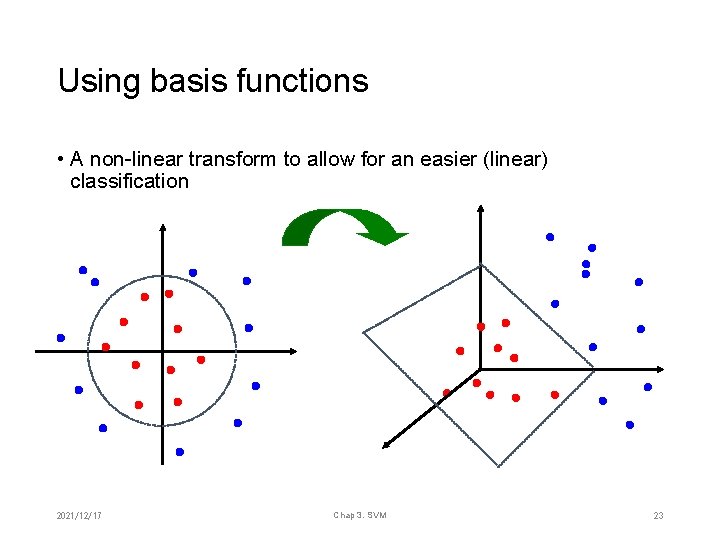
Using basis functions • A non-linear transform to allow for an easier (linear) classification 2021/12/17 Chap 3. SVM 23

SVM with basis functions • Consider to solve • The dual problem is • The solution is 2021/12/17 Chap 3. SVM 24

From basis function to kernel function • We notice that, all the basis functions appear in the form of inner product • We define the inner product of basis functions as which is termed kernel function • The space of basis function is then termed Reproducing Kernel Hilbert Space (RKHS) 2021/12/17 Chap 3. SVM 25

Kernel function: example • For example, we can prove that if is a kernel function • Since we can set , then • Similarly, we can prove the following kernel functions Radial-Basis Function 2021/12/17 Chap 3. SVM 26

Kernel function: benefit • For SVM (and alike), defining kernel function is equivalent to designing basis functions, which is termed kernel trick • Sometimes it is easier to express in kernel function than in basis function, for example RBF kernel • Sometimes we can prove a function is a kernel function, but it is difficult to write out its corresponding basis function • If a function satisfies the Mercer’s condition, it is a kernel function 2021/12/17 Chap 3. SVM 27

Kernelized SVM • The dual problem is • Once solved, we have 2021/12/17 Chap 3. SVM 28

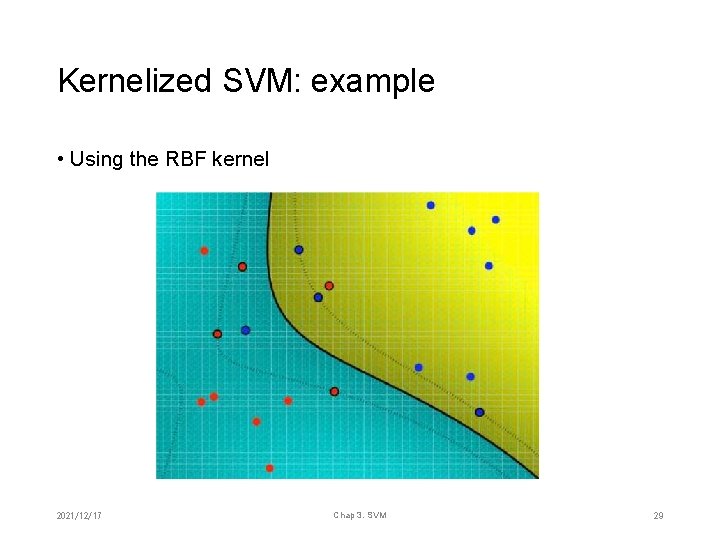
Kernelized SVM: example • Using the RBF kernel 2021/12/17 Chap 3. SVM 29

More about the kernel trick • There are many problems that can be formulated using the kernel trick, i. e. using kernel function to replace basis function • The Representation Theorem claims that, the solution to can be expressed as 2021/12/17 Chap 3. SVM 30

Chapter 3. Support Vector Machine (SVM) 1. 2. 3. 4. Max-margin linear classification Soft-margin linear classification The kernel trick Efficient algorithm for SVM 2021/12/17 Chap 3. SVM 31

SMO algorithm • The (dual) problem is • For this problem, sequential minimal optimization (SMO) is an efficient algorithm • Choose two Lagrange multipliers as variables, optimize over them while keeping the other multipliers unchanged, and iterate 2021/12/17 Chap 3. SVM 32

SMO algorithm: considering two variables • Due to the KKT condition, we have either • And our objective is a quadratic function 2021/12/17 Chap 3. SVM or 33

Chapter summary Dictionary Toolbox • Kernel trick • Margin; geometric ~; soft ~ • Mercer’s condition • Representation theorem • Reproducing kernel Hilbert space (RKHS) • Slack variable • Support vector • Hinge loss • Kernel function • Lagrange dual • Sequential minimal optimization (SMO) 2021/12/17 Chap 3. SVM 34