Solicitacin Axil Introduccin Ejercicios de Aplicacin Curso de

Solicitación Axil Introducción Ejercicios de Aplicación Curso de Estabilidad IIb Ing. Gabriel Pujol Para las carreas de Ingeniería Mecánica e Ingeniería Naval y Mecánica de la Facultad de Ingeniería de la Universidad de Buenos Aires

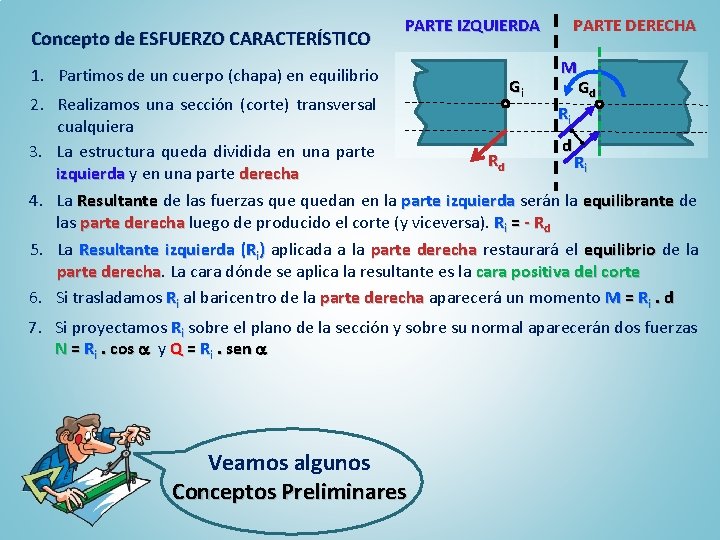
Concepto de ESFUERZO CARACTERÍSTICO PARTE IZQUIERDA 1. Partimos de un cuerpo (chapa) en equilibrio Gi PARTE DERECHA M Gd 2. Realizamos una sección (corte) transversal Ri cualquiera d 3. La estructura queda dividida en una parte Rd Ri izquierda y en una parte derecha 4. La Resultante de las fuerzas quedan en la parte izquierda serán la equilibrante de las parte derecha luego de producido el corte (y viceversa). Ri = - Rd 5. La Resultante izquierda (Ri) aplicada a la parte derecha restaurará el equilibrio de la parte derecha La cara dónde se aplica la resultante es la cara positiva del corte 6. Si trasladamos Ri al baricentro de la parte derecha aparecerá un momento M = Ri. d 7. Si proyectamos Ri sobre el plano de la sección y sobre su normal aparecerán dos fuerzas N = Ri. cos y Q = Ri. sen Veamos algunos Conceptos Preliminares

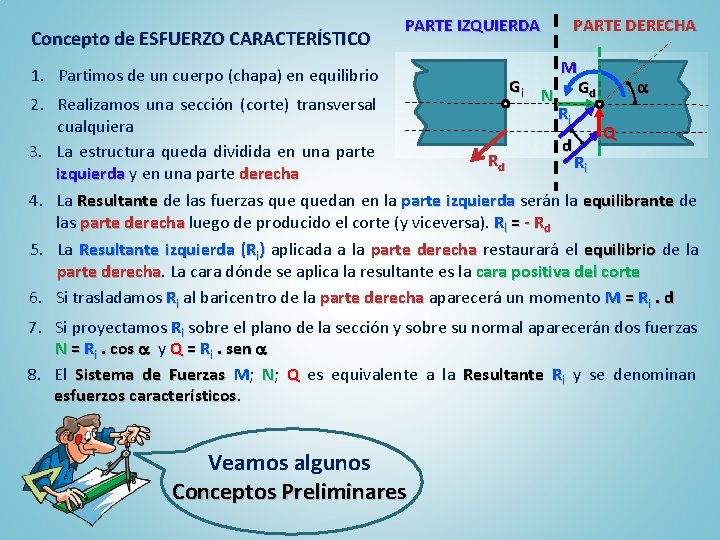
Concepto de ESFUERZO CARACTERÍSTICO PARTE IZQUIERDA 1. Partimos de un cuerpo (chapa) en equilibrio Gi N PARTE DERECHA M Gd 2. Realizamos una sección (corte) transversal Ri cualquiera Q d 3. La estructura queda dividida en una parte Rd Ri izquierda y en una parte derecha 4. La Resultante de las fuerzas quedan en la parte izquierda serán la equilibrante de las parte derecha luego de producido el corte (y viceversa). Ri = - Rd 5. La Resultante izquierda (Ri) aplicada a la parte derecha restaurará el equilibrio de la parte derecha La cara dónde se aplica la resultante es la cara positiva del corte 6. Si trasladamos Ri al baricentro de la parte derecha aparecerá un momento M = Ri. d 7. Si proyectamos Ri sobre el plano de la sección y sobre su normal aparecerán dos fuerzas N = Ri. cos y Q = Ri. sen 8. El Sistema de Fuerzas M; N; Q es equivalente a la Resultante Ri y se denominan esfuerzos característicos Veamos algunos Conceptos Preliminares

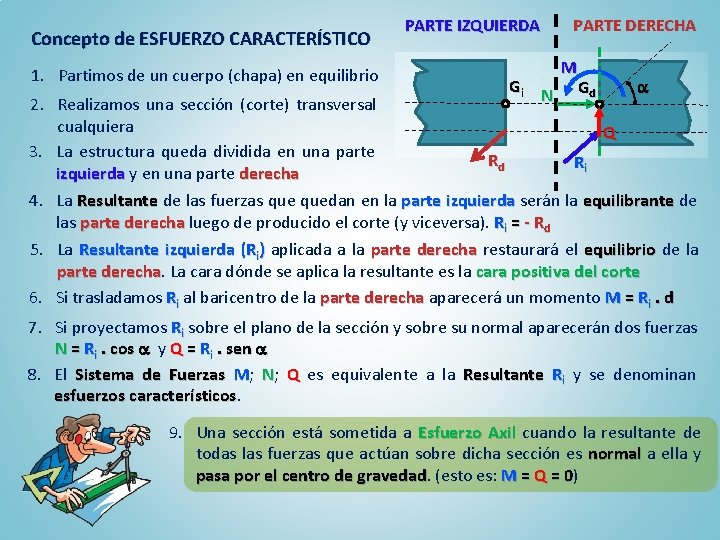
Concepto de ESFUERZO CARACTERÍSTICO 1. Partimos de un cuerpo (chapa) en equilibrio PARTE IZQUIERDA Gi N PARTE DERECHA M Gd 2. Realizamos una sección (corte) transversal cualquiera Q 3. La estructura queda dividida en una parte Rd Ri izquierda y en una parte derecha 4. La Resultante de las fuerzas quedan en la parte izquierda serán la equilibrante de las parte derecha luego de producido el corte (y viceversa). Ri = - Rd 5. La Resultante izquierda (Ri) aplicada a la parte derecha restaurará el equilibrio de la parte derecha La cara dónde se aplica la resultante es la cara positiva del corte 6. Si trasladamos Ri al baricentro de la parte derecha aparecerá un momento M = Ri. d 7. Si proyectamos Ri sobre el plano de la sección y sobre su normal aparecerán dos fuerzas N = Ri. cos y Q = Ri. sen 8. El Sistema de Fuerzas M; N; Q es equivalente a la Resultante Ri y se denominan esfuerzos característicos 9. Una sección está sometida a Esfuerzo Axil cuando la resultante de todas las fuerzas que actúan sobre dicha sección es normal a ella y pasa por el centro de gravedad (esto es: M = Q = 0) 0

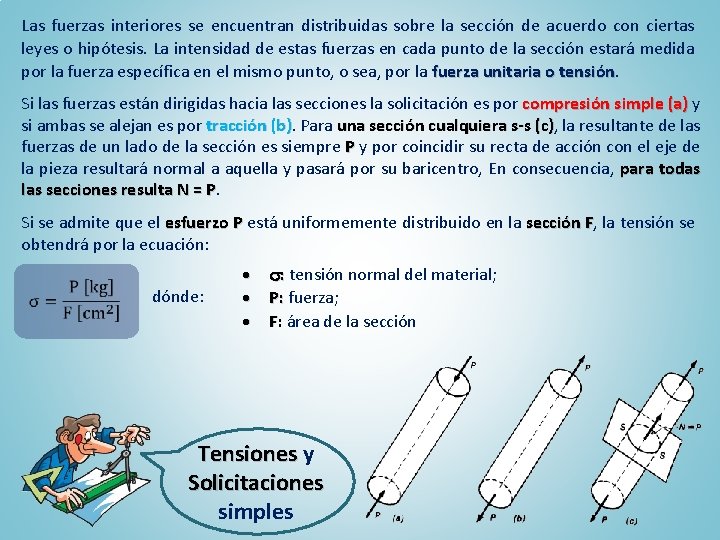
Las fuerzas interiores se encuentran distribuidas sobre la sección de acuerdo con ciertas leyes o hipótesis. La intensidad de estas fuerzas en cada punto de la sección estará medida por la fuerza específica en el mismo punto, o sea, por la fuerza unitaria o tensión Si las fuerzas están dirigidas hacia las secciones la solicitación es por compresión simple (a) y si ambas se alejan es por tracción (b). b) Para una sección cualquiera s-s (c), (c) la resultante de las fuerzas de un lado de la sección es siempre P y por coincidir su recta de acción con el eje de la pieza resultará normal a aquella y pasará por su baricentro, En consecuencia, para todas las secciones resulta N = P. P Si se admite que el esfuerzo P está uniformemente distribuido en la sección F, la tensión se obtendrá por la ecuación: dónde: : tensión normal del material; P: fuerza; F: área de la sección Tensiones y Solicitaciones simples

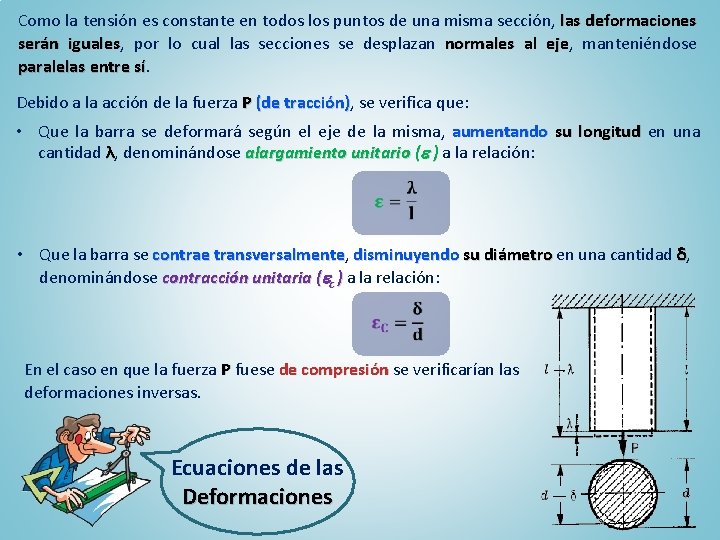
Como la tensión es constante en todos los puntos de una misma sección, las deformaciones serán iguales, iguales por lo cual las secciones se desplazan normales al eje, eje manteniéndose paralelas entre sí. sí Debido a la acción de la fuerza P (de tracción), tracción) se verifica que: • Que la barra se deformará según el eje de la misma, aumentando su longitud en una cantidad λ, denominándose alargamiento unitario (e ) a la relación: • Que la barra se contrae transversalmente, transversalmente disminuyendo su diámetro en una cantidad , denominándose contracción unitaria (ec ) a la relación: En el caso en que la fuerza P fuese de compresión se verificarían las deformaciones inversas. Ecuaciones de las Deformaciones

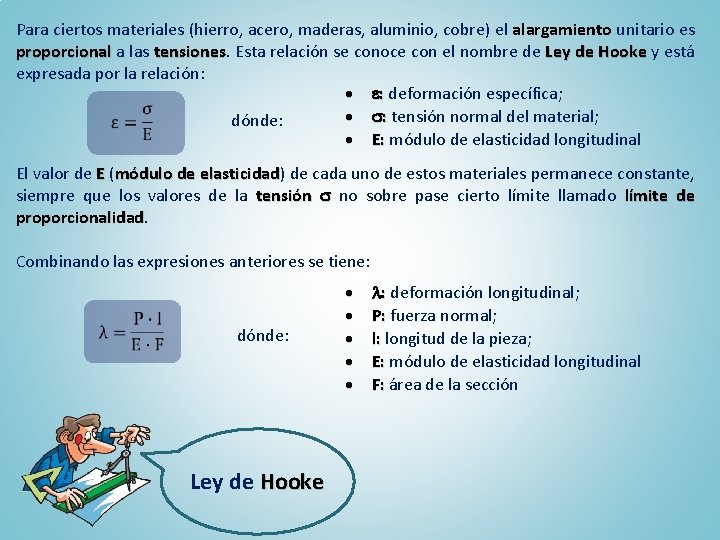
Para ciertos materiales (hierro, acero, maderas, aluminio, cobre) el alargamiento unitario es proporcional a las tensiones Esta relación se conoce con el nombre de Ley de Hooke y está expresada por la relación: e: deformación específica; : tensión normal del material; dónde: E: módulo de elasticidad longitudinal El valor de E (módulo de elasticidad) elasticidad de cada uno de estos materiales permanece constante, siempre que los valores de la tensión no sobre pase cierto límite llamado límite de proporcionalidad Combinando las expresiones anteriores se tiene: dónde: Ley de Hooke l: deformación longitudinal; P: fuerza normal; l: longitud de la pieza; E: módulo de elasticidad longitudinal F: área de la sección

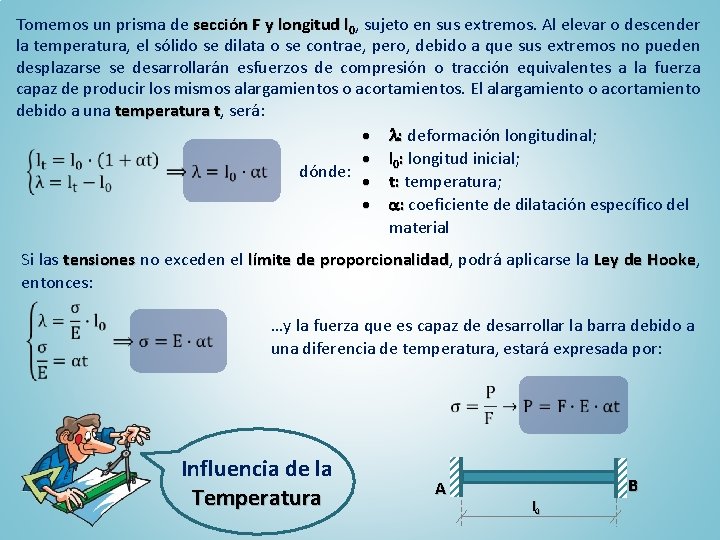
Tomemos un prisma de sección F y longitud l 0, sujeto en sus extremos. Al elevar o descender la temperatura, el sólido se dilata o se contrae, pero, debido a que sus extremos no pueden desplazarse se desarrollarán esfuerzos de compresión o tracción equivalentes a la fuerza capaz de producir los mismos alargamientos o acortamientos. El alargamiento o acortamiento debido a una temperatura t, t será: l: deformación longitudinal; l 0: longitud inicial; dónde: t: temperatura; : coeficiente de dilatación específico del material Si las tensiones no exceden el límite de proporcionalidad, proporcionalidad podrá aplicarse la Ley de Hooke, Hooke entonces: …y la fuerza que es capaz de desarrollar la barra debido a una diferencia de temperatura, estará expresada por: Influencia de la Temperatura A B l 0

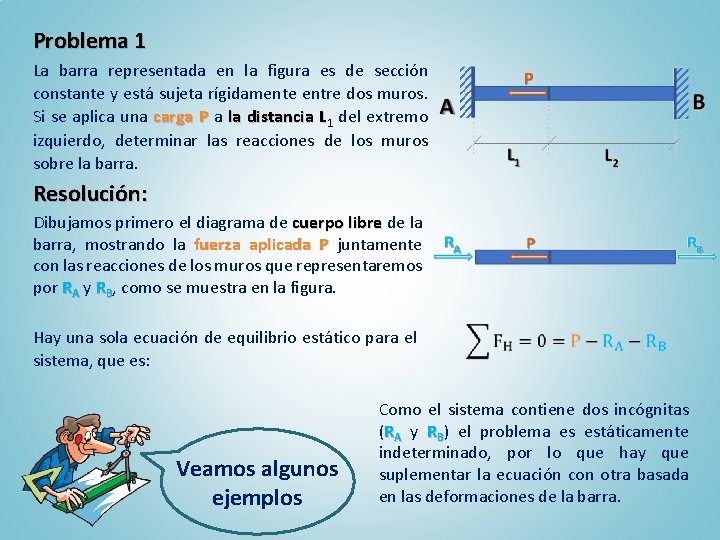
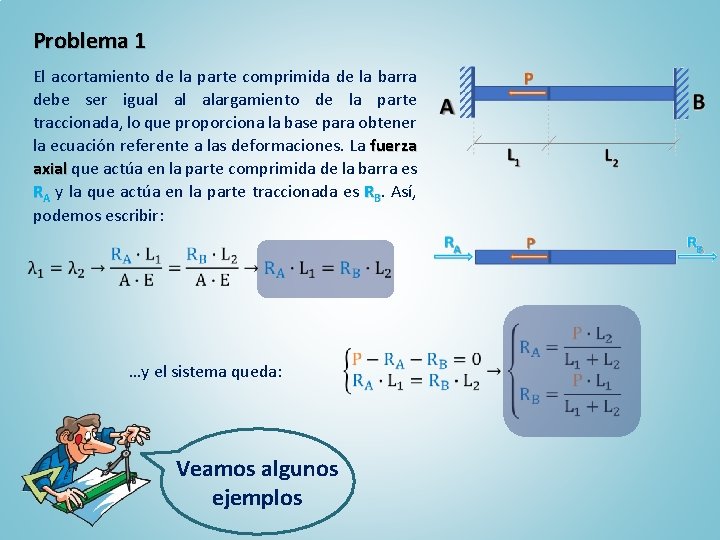
Problema 1 La barra representada en la figura es de sección constante y está sujeta rígidamente entre dos muros. Si se aplica una carga P a la distancia L 1 del extremo izquierdo, determinar las reacciones de los muros sobre la barra. Resolución: Dibujamos primero el diagrama de cuerpo libre de la barra, mostrando la fuerza aplicada P juntamente con las reacciones de los muros que representaremos por RA y RB, como se muestra en la figura. Hay una sola ecuación de equilibrio estático para el sistema, que es: Veamos algunos ejemplos Como el sistema contiene dos incógnitas (RA y RB) el problema es estáticamente indeterminado, por lo que hay que suplementar la ecuación con otra basada en las deformaciones de la barra.

Problema 1 El acortamiento de la parte comprimida de la barra debe ser igual al alargamiento de la parte traccionada, lo que proporciona la base para obtener la ecuación referente a las deformaciones. La fuerza axial que actúa en la parte comprimida de la barra es RA y la que actúa en la parte traccionada es RB. Así, podemos escribir: …y el sistema queda: Veamos algunos ejemplos

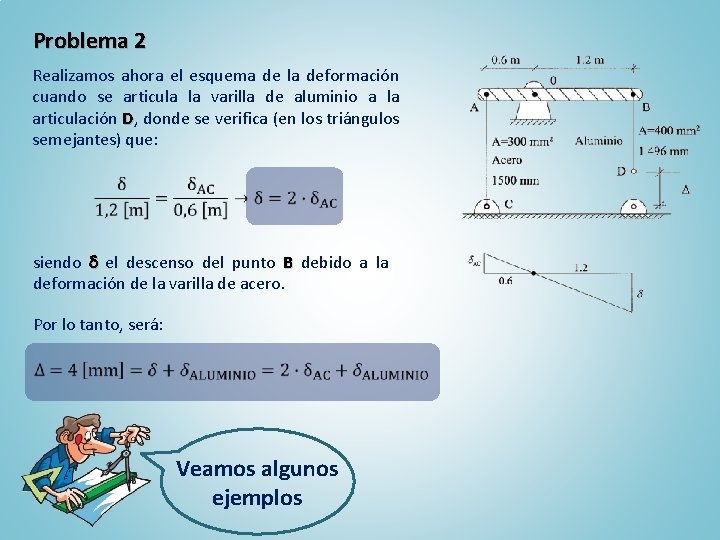
Problema 2 La barra rígida AB de peso despreciable estás articulada en O y fija a las varillas de acero y aluminio. Hay una separación = 4 mm entre la punta inferior de la varilla de aluminio y su articulación en D. Calcular el esfuerzo de la varilla de acero cuando la punta inferior de la varilla de aluminio se articula en el apoyo D. Datos: EAC = 200 GPa; GPa EAL = 70 GPa Resolución: Realizamos el diagrama de Cuerpo Libre, Libre y dado que el sistema se halla en equilibrio podemos plantear que: Veamos algunos ejemplos

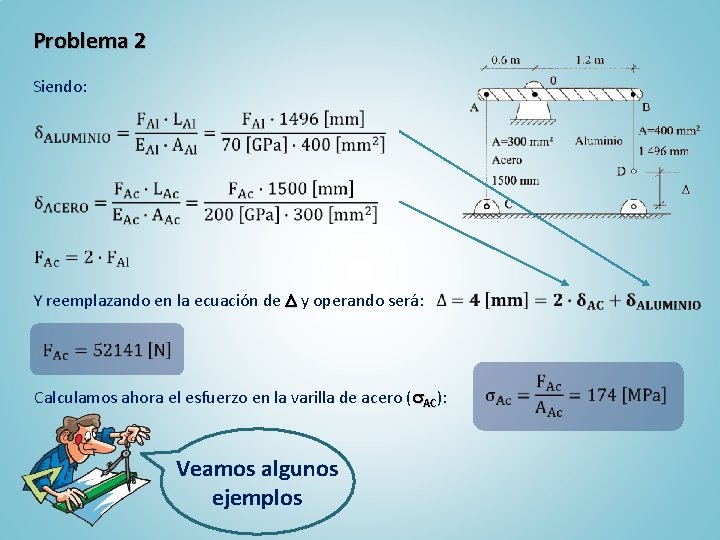
Problema 2 Realizamos ahora el esquema de la deformación cuando se articula la varilla de aluminio a la articulación D, donde se verifica (en los triángulos semejantes) que: siendo el descenso del punto B debido a la deformación de la varilla de acero. Por lo tanto, será: Veamos algunos ejemplos

Problema 2 Siendo: Y reemplazando en la ecuación de y operando será: Calculamos ahora el esfuerzo en la varilla de acero ( AC): Veamos algunos ejemplos

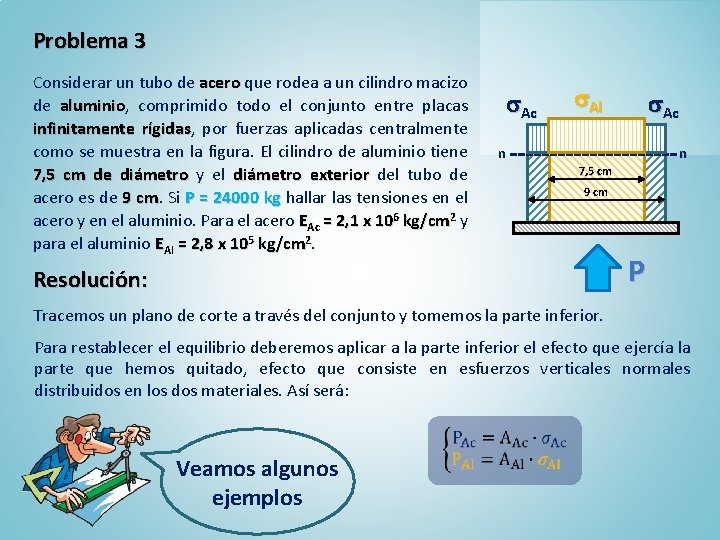
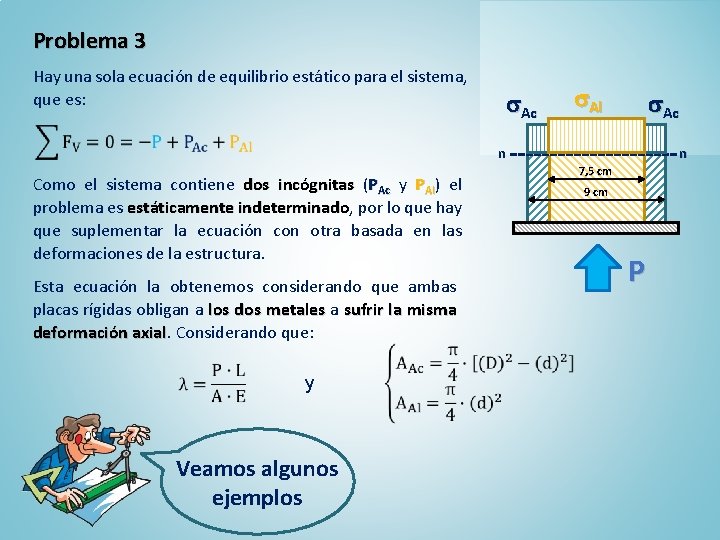
Problema 3 Considerar un tubo de acero que rodea a un cilindro macizo de aluminio, aluminio comprimido todo el conjunto entre placas infinitamente rígidas, rígidas por fuerzas aplicadas centralmente como se muestra en la figura. El cilindro de aluminio tiene 7, 5 cm de diámetro y el diámetro exterior del tubo de acero es de 9 cm. cm Si P = 24000 kg hallar las tensiones en el acero y en el aluminio. Para el acero EAc = 2, 1 x 106 kg/cm 2 y para el aluminio EAl = 2, 8 x 105 kg/cm 2. P Ac Al Ac n n 7, 5 cm 9 cm Resolución: P Tracemos un plano de corte a través del conjunto y tomemos la parte inferior. Para restablecer el equilibrio deberemos aplicar a la parte inferior el efecto que ejercía la parte que hemos quitado, efecto que consiste en esfuerzos verticales normales distribuidos en los dos materiales. Así será: Veamos algunos ejemplos

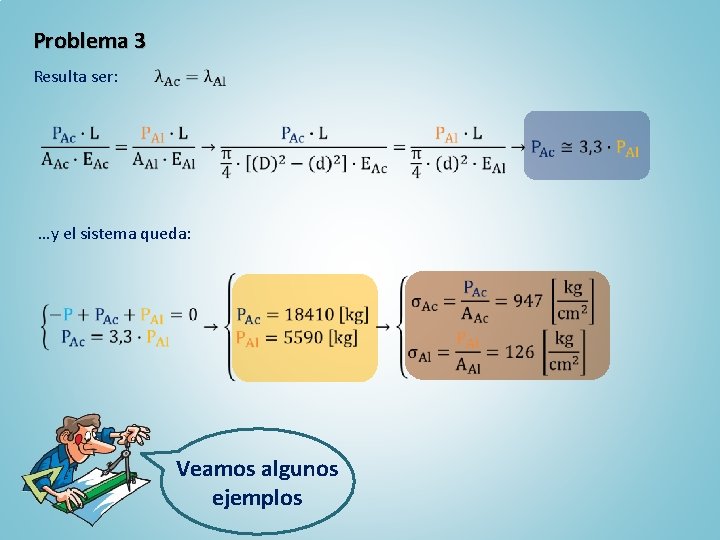
Problema 3 P Hay una sola ecuación de equilibrio estático para el sistema, que es: Ac Al Ac n Como el sistema contiene dos incógnitas (PAc y PAl) el problema es estáticamente indeterminado, indeterminado por lo que hay que suplementar la ecuación con otra basada en las deformaciones de la estructura. Esta ecuación la obtenemos considerando que ambas placas rígidas obligan a los dos metales a sufrir la misma deformación axial Considerando que: y Veamos algunos ejemplos n 7, 5 cm 9 cm P

Problema 3 Resulta ser: …y el sistema queda: Veamos algunos ejemplos

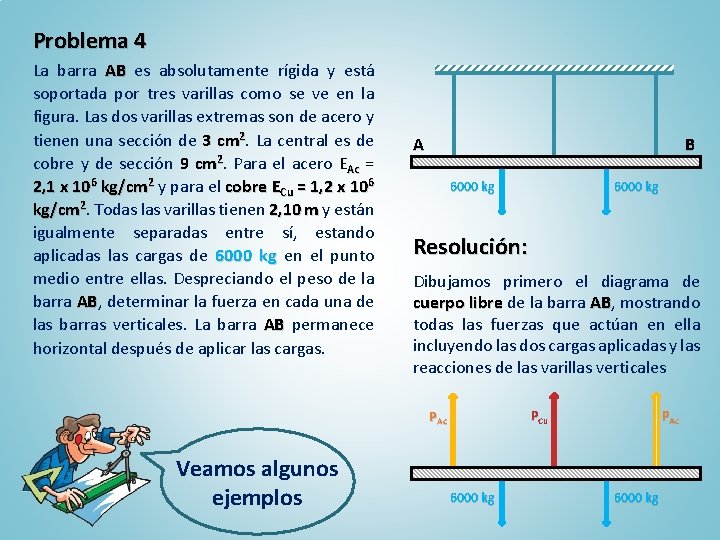
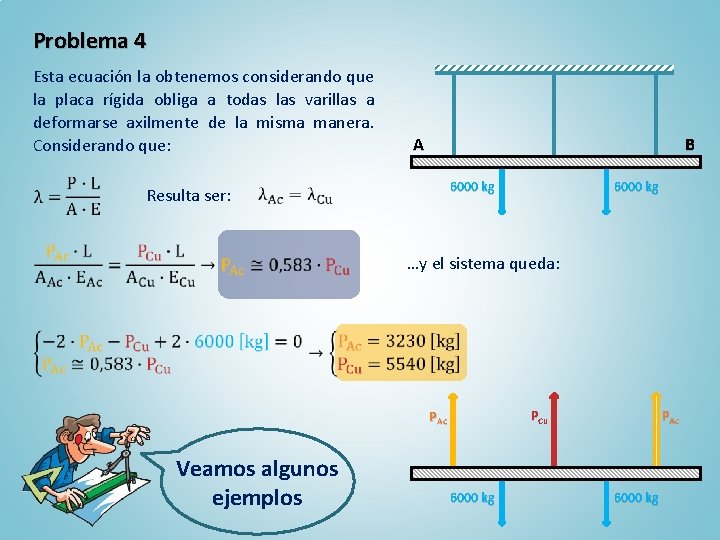
Problema 4 La barra AB es absolutamente rígida y está soportada por tres varillas como se ve en la figura. Las dos varillas extremas son de acero y tienen una sección de 3 cm 2. La central es de cobre y de sección 9 cm 2. Para el acero EAc = 2, 1 x 106 kg/cm 2 y para el cobre ECu = 1, 2 x 106 kg/cm 2. Todas las varillas tienen 2, 10 m y están igualmente separadas entre sí, estando aplicadas las cargas de 6000 kg en el punto medio entre ellas. Despreciando el peso de la barra AB, AB determinar la fuerza en cada una de las barras verticales. La barra AB permanece horizontal después de aplicar las cargas. A B 6000 kg Resolución: Dibujamos primero el diagrama de cuerpo libre de la barra AB, AB mostrando todas las fuerzas que actúan en ella incluyendo las dos cargas aplicadas y las reacciones de las varillas verticales PCu PAc Veamos algunos ejemplos 6000 kg PAc 6000 kg

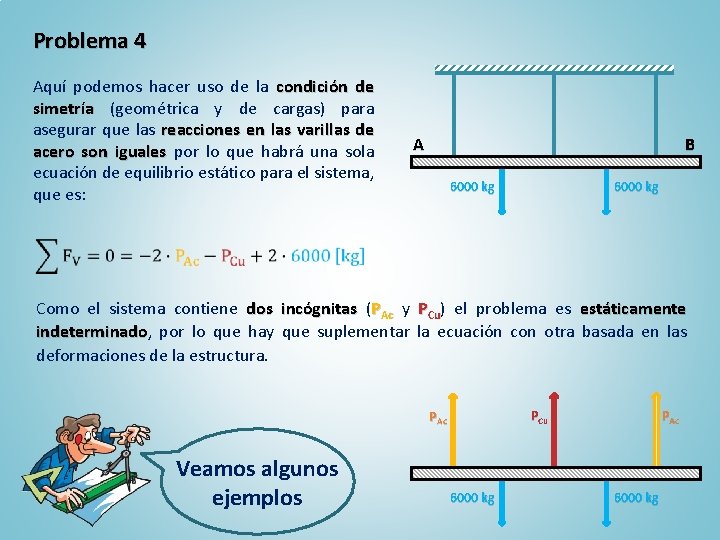
Problema 4 Aquí podemos hacer uso de la condición de simetría (geométrica y de cargas) para asegurar que las reacciones en las varillas de acero son iguales por lo que habrá una sola ecuación de equilibrio estático para el sistema, que es: A B 6000 kg Como el sistema contiene dos incógnitas (PAc y PCu) el problema es estáticamente indeterminado, indeterminado por lo que hay que suplementar la ecuación con otra basada en las deformaciones de la estructura. PCu PAc Veamos algunos ejemplos 6000 kg PAc 6000 kg

Problema 4 Esta ecuación la obtenemos considerando que la placa rígida obliga a todas las varillas a deformarse axilmente de la misma manera. Considerando que: A B 6000 kg Resulta ser: 6000 kg …y el sistema queda: PCu PAc Veamos algunos ejemplos 6000 kg PAc 6000 kg

Problema 5 Una barra de cobre tiene sección uniforme y está unida rígidamente a los muros como se ve en la figura. La longitud es de 150 cm y la sección de 15 cm 2. A la temperatura de 25 °C la varilla no tiene tensiones. Determinar las tensiones que existen en ella cuando la temperatura desciende 10 °C, °C suponiendo que los apoyos no ceden. Para el cobre ECu = 1, 1 x 106 kg/cm 2 y = 16 x 10 -6 1/°C A B 150 cm Resolución: El modo de resolver este problema es suponer que se corta la barra y se separa del muro en el extremo derecho. En este caso, es libre de contraerse cuando la temperatura desciende, reduciéndose la longitud Veamos algunos ejemplos

Problema 5 Ahora, es necesario hallar la fuerza axial P que hay que aplicar a la barra alargar a la barra 0, 036 cm, cm esto es, para volver a llevar el extremo derecho a su posición verdadera, porque sabemos que en realidad el extremo no se desplaza en absoluto al bajar la temperatura. Para determinar esta fuerza P, P utilizamos la ecuación: La tensión axil que produce esta fuerza es: Veamos algunos ejemplos P A B 150 cm

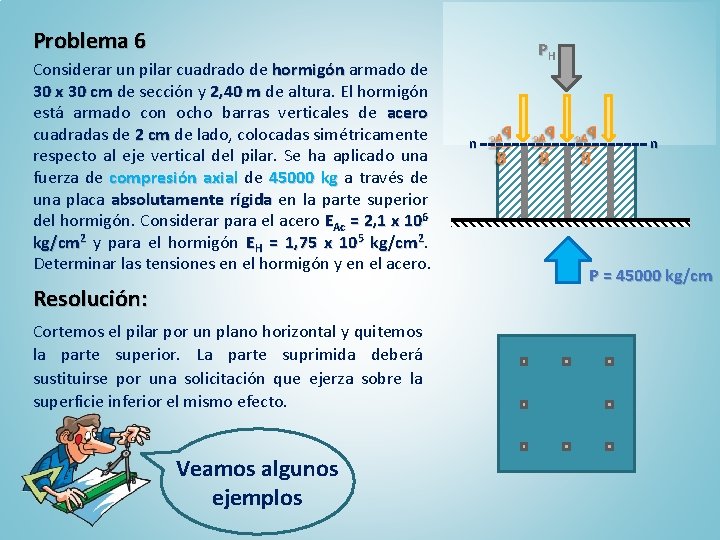
Problema 6 Considerar un pilar cuadrado de hormigón armado de 30 x 30 cm de sección y 2, 40 m de altura. El hormigón está armado con ocho barras verticales de acero cuadradas de 2 cm de lado, colocadas simétricamente respecto al eje vertical del pilar. Se ha aplicado una fuerza de compresión axial de 45000 kg a través de una placa absolutamente rígida en la parte superior del hormigón. Considerar para el acero EAc = 2, 1 x 106 kg/cm 2 y para el hormigón EH = 1, 75 x 105 kg/cm 2. Determinar las tensiones en el hormigón y en el acero. Resolución: Cortemos el pilar por un plano horizontal y quitemos la parte superior. La parte suprimida deberá sustituirse por una solicitación que ejerza sobre la superficie inferior el mismo efecto. Veamos algunos ejemplos PH n P = 45000 kg/cm

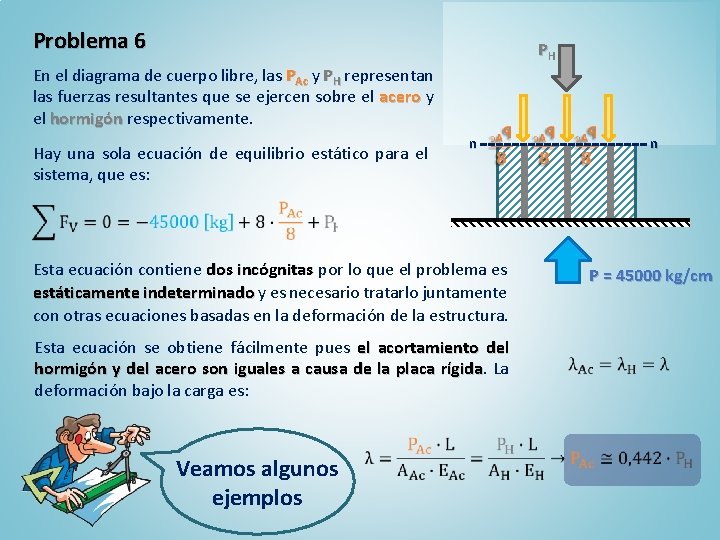
Problema 6 PH P En el diagrama de cuerpo libre, las PAc y PH representan las fuerzas resultantes que se ejercen sobre el acero y el hormigón respectivamente. Hay una sola ecuación de equilibrio estático para el sistema, que es: n Esta ecuación contiene dos incógnitas por lo que el problema es estáticamente indeterminado y es necesario tratarlo juntamente con otras ecuaciones basadas en la deformación de la estructura. Esta ecuación se obtiene fácilmente pues el acortamiento del hormigón y del acero son iguales a causa de la placa rígida La deformación bajo la carga es: Veamos algunos ejemplos n P = 45000 kg/cm

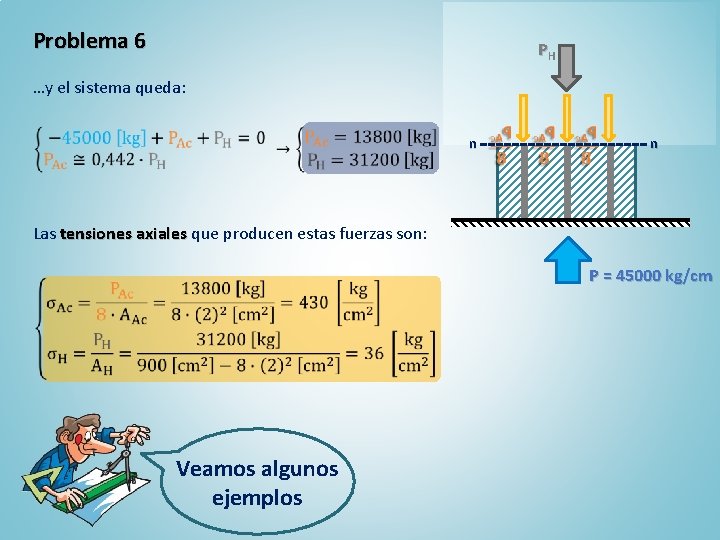
Problema 6 PH P …y el sistema queda: n n Las tensiones axiales que producen estas fuerzas son: P = 45000 kg/cm Veamos algunos ejemplos

Bibliografía Estabilidad II - E. Fliess Introducción a la estática y resistencia de materiales - C. Raffo Mecánica de materiales - F. Beer y otros Resistencia de materiales - R. Abril / C. Benítez Resistencia de materiales - Luis Delgado Lallemad / José M. Quintana Santana Resistencia de materiales - V. Feodosiev Resistencia de materiales - A. Pytel / F. Singer Resistencia de materiales - S. Timoshenko

Muchas Gracias